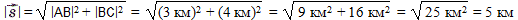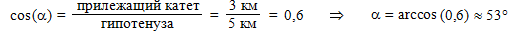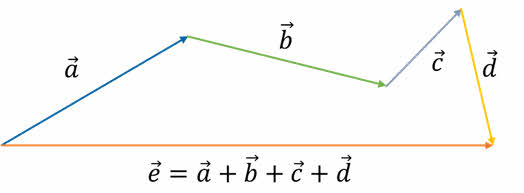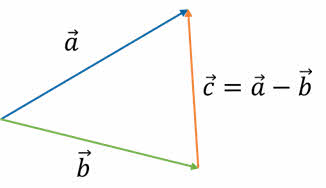Что такое перемещение физика 9 класс
Путь и перемещение тела
С понятием пути вы уже неоднократно сталкивались. Познакомимся теперь с новым для вас понятием – перемещением, которое более информативно и полезно в физике, чем понятие пути.
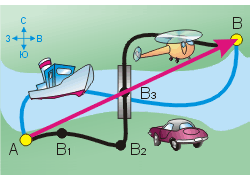
Допустим, из пункта А в пункт В на другом берегу реки нужно переправить груз. Это можно сделать на автомобиле через мост, на катере по реке или на вертолёте. В каждом из этих случаев путь, пройденный грузом, будет разным, но перемещение будет неизменным: из точки А в точку В.
Перемещением называют вектор, проведённый из начального положения тела в его конечное положение. Вектор перемещения показывает расстояние, на которое переместилось тело, и направление перемещения. Обратите внимание, что направление перемещения и направление движения – два разных понятия. Поясним это.
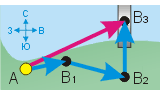
Рассмотрим, например, траекторию движения автомобиля от пункта А до середины моста. Обозначим промежуточные точки – В1, В2, В3 (см. рисунок). Вы видите, что на отрезке АВ1 автомобиль ехал на северо-восток (первая синяя стрелка), на отрезке В1В2 – на юго-восток (вторая синяя стрелка), а на отрезке В2В3 – на север (третья синяя стрелка). Итак, в момент проезда моста (точки В3) направление движения характеризовалось синим вектором В2В3, а направление перемещения – красным вектором АВ3.
Итак, перемещение тела – векторная величина, то есть имеющая пространственное направление и числовое значение (модуль). В отличие от перемещения, путь – скалярная величина, то есть имеющая только числовое значение (и не имеющая пространственного направления). Путь обозначают символом l, перемещение обозначают символом 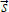
Почему в физике не ограничились понятием пути, а ввели более сложное (векторное) понятие перемещения? Зная модуль и направление перемещения, всегда можно сказать, где будет находиться тело (по отношению к своему начальному положению). Зная путь, положение тела определить нельзя. Например, зная лишь, что турист прошёл путь 7 км, мы ничего не можем сказать о том, где он сейчас находится.
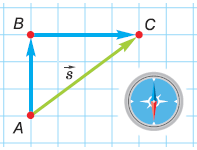
Задача. В походе по равнине турист прошёл на север 3 км, затем повернул на восток и прошел ещё 4 км. На каком расстоянии от начальной точки маршрута он оказался? Начертите его перемещение.
Решение 1 – с измерениями линейкой и транспортиром.
Перемещение – это вектор, соединяющий начальное и конечное положения тела. Начертим его на клетчатой бумаге в масштабе: 1 км – 1 см (чертёж справа). Измерив линейкой модуль построенного вектора, получим: 5 см. Согласно выбранному нами масштабу, модуль перемещения туриста равен 5 км. Но напомним: знать вектор – значит знать его модуль и направление. Поэтому, применив транспортир, определим: направление перемещения туриста составляет 53° с направлением на север (проверьте сами).
Решение 2 – без использования линейки и транспортира.
Поскольку угол между перемещениями туриста на север и на восток составляет 90°, применим теорему Пифагора и найдём длину гипотенузы, так как она одновременно является и модулем перемещения туриста:
Как видите, это значение совпадает с полученным в первом решении. Теперь определим угол α между перемещением (гипотенузой) и направлением на север (прилежащим катетом треугольника):
Итак, задача решена двумя способами с совпадающими ответами.
Презентация по физике для 9 класс на тему «Перемещение»
Описание презентации по отдельным слайдам:
Описание слайда:
Описание слайда:
Перемещение тела – это вектор, проведенный из начального положения тела в его конечное положение.
Перемещение тела
Описание слайда:
L- путь (скалярная величина)
Описание слайда:
Виды движения
Траектория – линия, которая показывает как движется тело.
криволинейное
прямолинейное
Описание слайда:
Различие между путём и перемещением
Путь – скаляр, а перемещение вектор.
Путь зависит от траектории, а перемещение нет.
Перемещение может быть положительным и отрицательным, а путь всегда строго положителен.
При движении тела путь может только увеличиваться, а модуль перемещения может как увеличиваться, так и уменьшаться.
Если тело вернулось в начальную точку, его перемещение равно нулю, а путь нулю не равен.
Описание слайда:
Описание слайда:
Описание слайда:
Задача. Автомобиль переместился из точки с координатой Х0=200м в точку с координатой Х=-200м.
Определите проекцию перемещения автомобиля.
Дано:
Х0=200 м
Х=-200 м
Описание слайда:
1. Что является траекторией движения молекулы воздуха?
1) Прямая
2) Дуга окружности
3) Дуга параболы
4) Ломаная линия
2. Утром вы выходите из дома, а вечером снова возвращаетесь. Что больше: пройденный вами путь или модуль перемещения?
1) Пройденный путь
2) Модуль перемещения
3) Они равны
4) Для ответа не хватает данных
3. Как должно двигаться тело, чтобы пройденный путь был равен модулю перемещения?
1) По прямой
2) По окружности
3) По прямой, не и меняя направления движения
4) По кривой линии
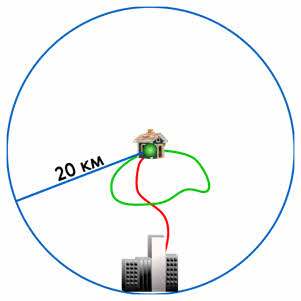
4. Ракета поднялась на высоту 20 км и вернулась на Землю в точку старта. Определите модуль перемещения ракеты.
1) 0 км
2) 10 км
3) 20 км
4) 40 км
5. Ракета поднялась на высоту 15 км и вернулась на Землю в точку старта. Определите пройденный ракетой путь.
1) 0 км
2) 7,5 км
3) 15 км
4) 30 км
6. Турист прошел по горизонтальному полю 400 м строго на север, затем еще 300 м на восток. Найдите пройденный туристом путь.
1) 300 м
2) 400 м
3) 500 м
4) 700 м
7. Турист прошел по горизонтальному полю 4 км строго на север, затем еще 3 км на восток. Найдите модуль перемещения туриста.
1) 3 км
2) 4 км
3) 5 км
4) 7 км
Описание слайда:
1-4, 2-1, 3-3, 4-1, 5-4, 6-4, 7-3, 8-4, 9-1, 10-3.
«Перемещение. Траектория. Путь» (9-й класс)
Разделы: Физика
Класс: 9
Демонстрации: Определение перемещения и пройденного пути.
1. Актуализация знаний.
– Здравствуйте, ребята! Садитесь! Сегодня мы с вами продолжим изучать тему “Законы взаимодействия и движения тел” и на уроке познакомимся с тремя новыми понятиями (терминами), касающихся этой темы. А пока проверим выполнение вами домашнего задания у данному уроку.
2. Проверка домашнего задания.
Перед уроком один учащийся выписывает на доске решение следующего домашнего задания:
Двум учащимся раздаются карточки с индивидуальными заданиями, которые выполняются во время устной проверки упр. 1 стр. 9 учебника. [1]
1. Какую систему координат(одномерную, двухмерную, трехмерную) следует выбрать для определения положения тел:
а) трактор в поле;
б) вертолет в небе;
в) поезд
г) шахматная фигура на доске.
2. Дано выражение: S = υ0 · t + (а · t 2 ) / 2, выразите: а, υ0
1. Какую систему координат (одномерную, двухмерную, трехмерную) следует выбрать для определения положения таких тел:
а) люстра в комнате;
б) лифт;
в) подводная лодка;
г) самолет на взлетной полосе.
3. Изучение нового теоретического материала.
С изменениями координат тела связана величина, вводимая для описания движения, – ПЕРЕМЕЩЕНИЕ.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Перемещение принято обозначать буквой 
[ 
Перемещение – величина векторная, т.е. кроме числового значения имеет еще и направление. Векторную величину изображают в виде отрезка, который начинается в некоторой точке и заканчивается острием, указывающим направление. Такой отрезок-стрелка называется вектором.

Знать вектор перемещения – значит, знать его направление и модуль. Модуль вектора – это скаляр, т.е. численное значение. Зная начальное положение и вектор перемещения тела, можно определить, где находится тело.
В процессе движения материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом движущаяся точка “описывает” в пространстве какую-то линию. Иногда эта линия видна, – например, высоко летящий самолет может оставлять за собой след в небе. Более знакомый пример – след куска мела на доске.
Воображаемая линия в пространстве, по которой движется тело называется ТРАЕКТОРИЕЙ движения тела.
Траектория движения тела – это непрерывная линия, которую описывает движущееся тело (рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.
Движение, при котором все точки тела движутся по одинаковым траекториям, называется поступательным.
Очень часто траектория – невидимая линия. Траектория движущейся точки может быть прямой или кривой линией. Соответственно форме траектории движение бывает прямолинейным и криволинейным.
Длина траектории – это ПУТЬ. Путь является скалярной величиной и обозначается буквой l. Путь увеличивается, если тело движется. И остается неизменным, если тело покоится. Таким образом, путь не может уменьшаться с течением времени.
Модуль перемещения и путь могут совпадать по значению, только в том случае, если тело движется вдоль прямой в одном направлении.
Чем же отличается путь от перемещения? Эти два понятия часто смешивают, хотя на самом деле они очень сильно отличаются друг от друга. Рассмотрим эти отличия: (Приложение 3) (раздаются в виде карточек каждому ученику)
| Путь | Перемещение | |
| Определение | Длина траектории, описываемой телом за определенное время | Вектор, соединяющий начальное положение тела с его последующим положением |
| Обозначение | l [ м ] | S [м ] |
| Характер физических величин | Скалярная, т.е. определяется только числовым значением | Векторная, т.е. определяется числовым значением (модулем) и направлением |
| Необходимость введения | Зная начальное положение тела и путь l, пройденный за промежуток времени t, нельзя определить положение тела в заданный момент времени t | Зная начальное положение тела и S за промежуток времени t, однозначно определяется положение тела в заданный момент времени t |
| l = S в случае прямолинейного движения без возвратов | ||
4. Демонстрация опыта (учащиеся выполняют самостоятельно на своих местах за партами, учитель вместе с учащимися выполняет демонстрацию этого опыта)
5. Упражнения и вопросы для повторения.
Повторение понятий урока:
– перемещение;
– траектория;
– путь.
7. Домашнее задание.
§ 2 учебника [1], вопросы после параграфа, упражнение 2 (стр.12) учебника [1], повторить выполнение опыта урока дома.
1. Перышкин А.В., Гутник Е.М. Физика. 9 кл.: учеб.для общеобразоват.учреждений – 9-е изд., стереотип. – М.: Дрофа, 2005.
Перемещение
Урок 2. Физика 9 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Перемещение»
В процессе механического движения положение тела в пространстве меняется с течением времени. До сегодняшнего дня при решении большинства задач на движение тел, мы использовали понятие «путь». Оно вам хорошо известно. Напомним, что путь — это длина траектории, пройденной телом за время наблюдения.
А траектория — это воображаемая линия в пространстве, по которой движется тело.
Путь чаще всего обозначают малой латинской буквой s, а единицей пути в СИ является метр.
Путь — это скалярная величина, то есть величина, имеющая числовое значение, но не имеющая направления.
Положение тела через некоторый промежуток времени можно определить, зная траекторию движения, начальное положение тела на траектории и пройденный телом за этот промежуток времени путь. Если же траектория движения тела неизвестна, то его положение в некоторый момент времени определить нельзя, поскольку один и тот же путь тело может пройти в разных направлениях. Покажем это.
Пусть, например, из лыжной базы в 20 километрах к северу от города вышел лыжник и за 2,5 часа прошёл 20 километров пути. Как определить, куда он пришёл? Ведь он мог находиться в различных местах, удалённых от лыжной базы не более чем на 20 километров. Он мог дойти, например, до города. А мог, пройдя в каком-либо направлении 10 километров, вернуться на базу. В любом случае путь будет равен 20 километрам, но положение лыжника в пространстве будет разным.
Поэтому для определения положения лыжника нам необходимо знать направление его движения и расстояние, пройденное им в этом направлении. Направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением, называется перемещением тела.
Таким образом, перемещение — это векторная величина, то есть имеет направление и числовое значение (модуль).
Обозначается перемещение, как и путь, малой латинской буквой s, только со стрелочкой над ней. Единицей перемещения в СИ является метр.
Таким образом, если знать начальное положение тела и его перемещение за некоторый промежуток времени, то можно легко определить положение тела в конце этого промежутка времени.
— А как складываются или вычитаются между собой пути и как перемещения?
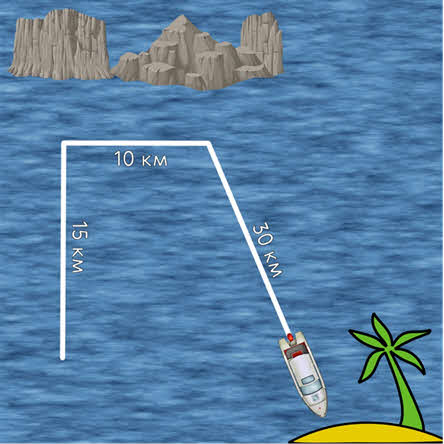
Так как путь — это величина скалярная, то пройденные пути складываются и вычитаются арифметически. Например, если известно, что катер проплыл 10 километров на север. Затем 15 километров на восток и ещё 30 километров на юго-восток, то общий путь, пройденный катером, равен 55 километрам.
Перемещения же складываются и вычитаются по правилам сложения и вычитания векторов.
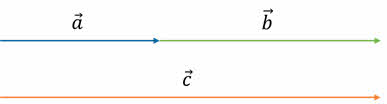
Давайте вспомним, как складываются векторы. Итак, если два вектора направлены одинаково, то их сумма — это вектор того же направления, имеющий модуль, равный сумме модулей данных двух векторов.
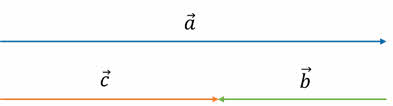
Если же направления векторов противоположны, то их сумма — это вектор, который направлен так же, как вектор, модуль которого больше. При этом модуль полученного вектора равен разности модулей слагаемых векторов.
— А как сложить векторы, направленные под углом друг к другу?
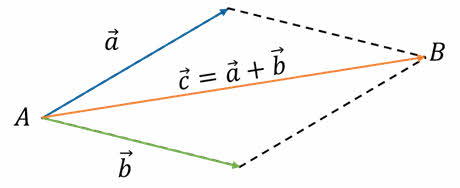
Для этого существуют несколько правил. Первое называется правилом параллелограмма.
Чтобы сложить два вектора по этому правилу, необходимо параллельным переносом совместить начала слагаемых векторов. Затем построить параллелограмм, принимая складываемые векторы за его стороны. Суммой векторов будет являться вектор, совпадающий с большей диагональю параллелограмма.
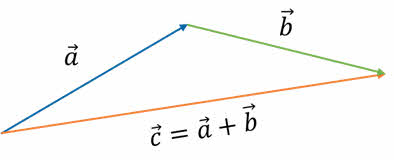
Второе правило называется правилом треугольника. Чтобы сложить два вектора по этому правилу, необходимо параллельным переносом совместить конец одного вектора с началом второго вектора. Вектор, проведённый из начала вектора а в конец вектора b, и равен их сумме.
Если нам требуется найти сумму нескольких векторов, то необходимо параллельным переносом совместить векторы так, чтобы каждый следующий вектор выходил из конца предыдущего. Замыкающий вектор, проведённый из начала первого вектора в конец последнего, и есть искомая сумма данных векторов. Такой способ сложения называется правилом многоугольника.
Ну и наконец, если требуется найти разность двух векторов, необходимо параллельным переносом совместить начала векторов a и b. А затем провести вектор из конца вычитаемого вектора в конец уменьшаемого вектора.
Вспомнив правила сложения и вычитания векторов, мы можем утверждать, что общем случае, перемещение не совпадает с траекторией движения тела. А модуль перемещения — с пройденным путём.
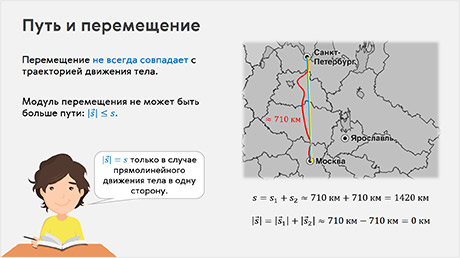
Например, пусть автомобиль отправился из Москвы в Санкт-Петербург и вернулся обратно. Кратчайший автомобильный маршрут от центра Москвы до центра Санкт-Петербурга имеет протяжённость 710 километров. Поэтому путь, который проехал автомобиль, составляет 1420 километров. А вот его перемещение равно нулю. Поэтому помните, что модуль перемещения и пройденный путь равны только в том случае, если тело движется по прямолинейной траектории в одну сторону. Иными словами, путь не может быть меньше модуля перемещения.
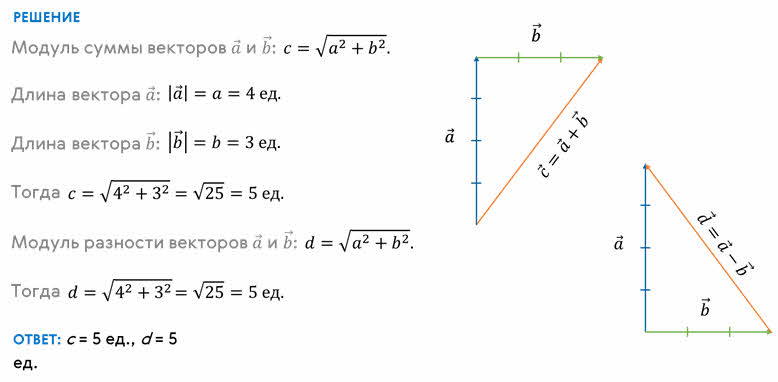
Определите сумму и разность взаимно перпендикулярных векторов a и b. Найдите модули векторов суммы их суммы и разности.
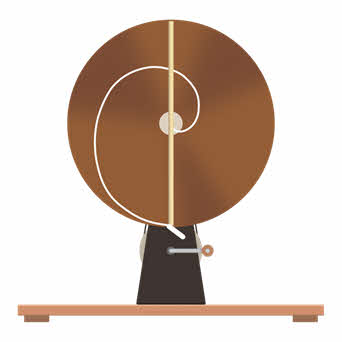
В заключении урока давайте посмотрим, зависит ли форма траектории, путь и перемещение от выбора системы отсчёта. Для этого проделаем такой опыт. Приложим к диску вертикальную рейку в его середине и раскрутим диск. Теперь проведём вдоль рейки мелом от центра диска вниз. При таком движении в системе отсчёта, связанной с Землёй, траекторией мела является прямая линия. А путь и модуль перемещения мела будут равны.
Однако на диске при этом вычерчивается спираль, которая показывает траекторию движения того же самого мела в системе отсчёта, связанной с диском, — и эта траектория является криволинейной.
Или вот ещё один опыт, описанный ещё в книге Галилея «Диалог о двух системах мира». Суть опыта в следующем. С вершины мачты плывущего корабля на его палубу падает ядро. В системе отсчёта, связанной с кораблём, траектория движения ядра — это прямолинейный отрезок. Однако с точки зрения наблюдателя, стоящего на берегу, ядро имело некоторую начальную горизонтальную скорость, равную скорости корабля. Поэтому траектория движения ядра криволинейная.
Таким образом, на этом примере мы видим, что форма траектории, путь и перемещение тела в различных системах отсчёта различны.
Урок по физике в 9 классе «Перемещение»
Урок по физике для 9 класса «Перемещение»
создать условия, которые позволяют сформировать у учащихся представления о связи физики с действительностью;
дать представление о следующих физических понятиях: пространство, время, путь, траектория, перемещение;
сформировать некоторые умения, связанные с применением изученных понятий при описании движения;
познакомить учащихся с историей физики по данной теме.
Диагностируемые цели урока.
о свойствах пространства и времени;
о том, что путь и перемещение это различные понятия;
знает о двух видах траектории движения;
переводить одни единицы времени в другие;
определять путь и перемещение;
рисовать траекторию движения;
построения вектора перемещения.
1. Мотивационно-ориентировочная часть.
Задача 1: Пропал ученик, известно, что он вышел из здания школы в 13:00, в момент времени 14:00 известно, что он прошел 3 км. Где на данный момент находится ученик?
2. Операционально-познавательная часть.
А) Пространство и время.
Во времени живя, мы времени не знаем.
Тем самым мы себя самих не понимаем.
В какое время мы, однако, родились?
Какое время нам прикажет: «Удались»?
А как нам распознать, что наше время значит
И что за будущее наше время прячет?
Весьма различны времена по временам:
То нечто, то ничто – они подобны нам.
Изжив себя в конец, рождает время время.
Так продолжается и человечье племя,
Но время времени нам кажется длинней
Коротким временем нам отведенных дней,
Подчас о времени мы рассуждаем с вами,
Но время – это мы! Никто иной. Мы с вами!
Знай: время без времен когда-нибудь придет
И нас из времени насильно уведет.
И мы, самих себя сваливши с плеч, как бремя.
Предстанем перед тем, над кем не властно время.
Человек давно научился определять время: ночью – по положению звезд, а днем – по длине тени, отбрасываемой предметами в разные часы дня. Солнечные часы – привычный атрибут центральных площадей античных городов. Небольшие промежутки времени измеряли переносными песочными или водяными часами, с XI в. в городах начали появляться механические часы с колесами и гирями. Карманные часы с боем появились в 1505 г., после того как мастер Петр Генлайн из Нюрнберга заменил гирю пружиной. Часы эти называли «нюрнбергскими яйцами». Первые маятниковые часы появились в XVII в.
Б) Траектория. Путь и перемещение.
Траектория – линия, которую описывает тело при движении.
Перемещение – направленный отрезок, соединяющий начальное и конечное положение тела. → s [м].
По виду траектории движение делится на:
Путь и перемещение
Выбран он мысленно,
В III в. в Китае изобрели прибор для измерения расстояний: легкая тележка имела систему зубчатых передач, соединенную с колесом и барабаном. Каждое «ли» (576 м) отмечалось ударом барабана. С помощью этого изобретения министр Пей Сю создал «Региональный атлас» на 18 листах и большую карту Китая на шелке, которая была так велика, что одному человеку было ее трудно развернуть.
Задача 1. Пропал ученик, известно, что он вышел из здания школы в 13:00, в момент времени 14:00 известно, что он прошел 3 км. Где на данный момент находится ученик, если известно, что он двигался на восток?
Задача 2. Длина беговой дорожки на стадионе 400 м. Определите путь и перемещение спортсмена, после того как он пробежал 800 м.
Задача 3. Нарисуйте траекторию движения Земли вокруг Солнца.
3. Рефлексивно-оценочная часть.
Удобно ли пользоваться такими часами?
— Самое несложное из всего! – ответил он (Коровьев). – Тем, кто хорошо знаком с пятым измерением, ничего не стоит раздвинуть помещение до желательных размеров.
(М.А.Булгаков. «Мастер и Маргарита»)
Чем отличается пространство Коровьева от нашего пространства? Перечислите основные свойства пространства.
(М.А.Булгаков. «Мастер и Маргарита»)
Какую систему координат применяем при игре в шахматы? Приведите примеры, когда применяются одномерные, двухмерные и трехмерные системы координат.
4)Там на неведомых дорожках
Следы невиданных зверей.
(А.С.Пушкин. «Руслан и Людмила»)
Можно ли по следам определить направление движения зверей? Что называется траекторией?
5)Уходит день – не привяжешь за плетень.
Дайте понятие времени и расскажите об основных свойствах времени.
7)Что может в одно и то же время:
Висеть и стоять, стоять и ходить,
Ходить и лежать, лежать и врать?
Какую физическую величину измеряют с помощью часов?
8) Стучит, гремит, вертится, ходит весь век, а не человек. (Часы)
Какие единицы времени вы знаете? Переведите эти единицы в секунды.
— Иванов, почему вы сегодня опоздали на работу?
— Да сынишку своего в детский садик с утра привел, оказалось – не в тот.
— Пошли в другой садик – опять не тот.
— Затем в третий, и снова не туда.
— А когда в четвертый пришли, сын мне и говорит: «Папа, еще один садик, и я в школу опоздаю!»
Оцените путь и перемещение ребенка после того как он попал в школу.
10). От асфальта до звезд
(Н.В.Рубцов. «Не пришла»)
Что представляют собой штрихи, образованные падением снега?
11). И в пространстве,
Из дивной дали гость –
Будто выведенным мелом,
(Н.Рубцов. «Утро перед экзаменом»)
О каких свойствах пространства упоминается в стихотворении?
12). Лакей, облокотившись на свое кресло, дремал на козлах, почтовый ямщик покрикивал бойко, гнал крупную потную четверку, изредка оглядываясь на другого ямщика, покрикивавшего сзади в коляске. Параллельные широкие следы шин ровно и шибко стлались по известковой грязи дороги.
(Л.Н.Толстой. «Три смерти»)
Что представляли собой следы шин на дороге?