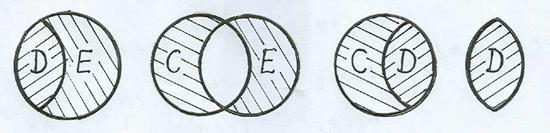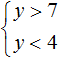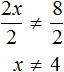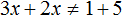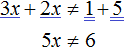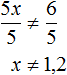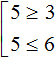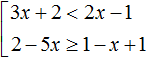Что такое пересечение множеств объединение разность
Что такое пересечение, объединение и разность множеств?
Пересечением двух множеств, называется третье множество, сформированное из элементов, которые входят в оба первых множества.
Например, если в одно множество входят числа от 1 до 10, а во второе — от 5 до 20, то пересечением этих множеств будут числа от 5 до 10, так как они входят в оба.
Пересечение множеств записывается так:
На диаграмме Эйлера-Венна пересечение множеств обозначается общей частью кругов.
Множества могут не пересекаться вообще, одно может полностью включать другое.
Пересечение множеств может использоваться тогда, когда надо найти элементы, которые удовлетворяют нескольким условиям.
Объединением двух множеств, называется третье множество, сформированное из всех элементов обоих первых множеств. При этом если элемент входит в оба множества, то в объединенное он входит один раз. Это и понятно, так как множество по определению включает только разные элементы.
Например, объединением множества натуральных чисел от 1 до 10 и множества натуральных от 5 до 15 будет множество натуральных чисел от 1 до 15.
Объединение множеств описывается так:
На диаграмме Эйлера-Венна объединение множеств обозначается всей областью кругов.
Разностью двух множеств, называют третье множество, в которое входят все элементы одного из двух множеств и не входят элементы принадлежащие обоим множествам.
Если результат пересечения и объединения двух множеств не меняется от перестановки множеств при выполнении операции, то результат разности зависит от того, какое множество из какого «вычитают».
Сравните. Даны множества A = <1,2,3,4,5>и B = <4,5,8,9>. Разность множеств обозначается знаком \.
A \ B = <1,2,3>, т. к. 4 и 5 входят в множество B.
В то время как B \ A = <8,9>.
Понятно, что если у множеств нет общих элементов, то их разность будет равна «уменьшаемому», т. е. первому множеству. Если же множества полностью совпадают, то их разностью будет пустое множество.
Если все элементы «вычитаемого» множества B входят в состав «уменьшаемого» A (A \ B), то B называют дополнением некого множества C до A.
Пересечение, объединение и разность множеств
Пересечение множеств
Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:
Объединение множеств
Объединением – множеств A и B называют множество, содержащее те и только те элементы, которые входят хотя бы в одно из множеств, A или B:
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
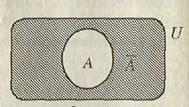
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:
При рассмотрении целочисленных задач, универсум – это множество целых чисел.
При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Свойства операций пересечения и объединения
$(A \cap B) \cap C = A \cap (B \cap C)$
$(A \cup B) \cap C = (A \cap C) \cup (B \cap C)$
Взаимодействие с отрицанием, пустым множеством и универсумом
$A \cap \varnothing = \varnothing$
$A \cup \varnothing = A$
Разность множеств
Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A \cup B) = n(A)+ n(B)-n(A \cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.
Примеры
Пример 1. Найдите пересечение данных множеств:
Операции над множествами: пересечение, объединение, разность, дополнение
1. Для задания множеств применяется еще один способ – с помощью теоретико-множественных операций, позволяющих строить из одних множеств другие. Рассмотрим несколько таких операций и их представления диаграммами Венна.
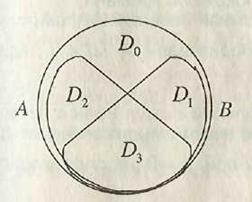
A. Пересечением двух множеств A и B называется множество М = A ∩ B, состоящее из элементов, принадлежащих обоим множествам: и множеству A, и множеству B. Пересечение – это общая часть двух множеств (область D на рис. 1.2). Аналогично определяется пересечение
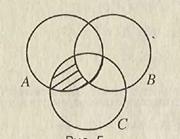
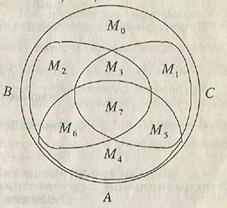
трех или более множеств (показано частой штриховкой на рис. 1.3). Символ ∩ означает операцию пересечения множеств.
Термин «пересечение» – по существу геометрического происхождения. Пересечением прямой и плоскости, если прямая не лежит на плоскости и не параллельна ей, является их единственная общая точка. Если прямая и плоскость параллельны, то их пересечение не содержит ни одной точки, т.е. пусто. Если же прямая имеет с плоскостью более одной общей точки, то, как известно, она целиком лежит на плоскости, и их пересечение совпадает с множеством точек этой прямой.
В этом случае множество точек прямой есть подмножество множества точек плоскости.
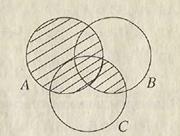
B. Объединением двух множеств A и B называется множество М = A È B, состоящее из всех элементов, принадлежащих хотя бы одному из множеств A или B (или обоим). При этом каждый элемент входит в объединение один раз. Символ È означает операцию объединения множеств (области С, D, E вместе на рис. 1.2). Объединение трех и более множеств определяется аналогично (показано редкой штриховкой на рис. 1.3).
C. Разностью М = A \ B двух множеств A и B называется множество, состоящее из всех элементов A, не принадлежащих B. Иначе говоря, чтобы получить разность, нужно из множества A удалить его общие элементы с множеством B (на рис. 1.2 разность A\B=C ). Разность B \ A – область E на рис. 1.2.
Симметрическую разность называют также суммой по модулю 2. Очевидно соотношение: АΔВ = (A È В) \ (A ∩ B).
На рис. 1.4 – частные случаи общей картины, изображенной на рис. 1.2.
Если С = A \ B = Æ, т.е. A Í B, то D = A, E = B \ A, (рис. 1.4, а).
Если E = B \ A = Æ, т.е. B Í A, то С = A \ B, D = B (рис. 1.4, в).
При равенстве множеств A и B и имеем C = E = Æ, D = A = B, (рис. 1.4, г).
E. Пусть A – некоторое множество в универсальном множестве U. Дополнением 
Примеры. 1. Пересечением множества 5-этажных домов и множества кирпичных домов является множество кирпичных пятиэтажек.
2. Пусть в множестве учеников школы (оно будет служить универсальным множеством U) A – подмножество учащихся, занимающихся спортом; B – подмножество учащихся, интересующихся музыкой; C – подмножество мальчиков. Тогда пересечению A ∩ B принадлежат все учащиеся, увлекающиеся и спортом, и музыкой; в пересечение A ∩ C входят мальчики, увлекающиеся музыкой; объединение A È B – множество учащихся, увлекающихся или спортом, или музыкой, или тем и другим; дополнение 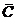
3. Пусть множество натуральных чисел A = <1, 2, 3, 4, 6, 8, 12, 24>– делители числа 24;
B = <1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90>– делители числа 90. Тогда пересечение
A ∩ B = <1, 2, 3, 6>– множество общих делителей этих чисел (6 – наибольший общий делитель).
С помощью введенных операций можно образовывать более сложные комбинации. Например, формула (A \ B)∩ C представляет множество элементов множества A, не принадлежащих B, но принадлежащих C (рис. 1.6); множество A È (B ∩ C) содержит все элементы, которые принадлежат A, а также общие элементы множеств B и C (рис. 1.7).
Упражнение. Сформулируйте словами, какие подмножества универсального множества U учеников школы (пример 2) представляются формулами 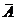
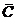
2. На диаграммах Венна легко проверить соотношения:
Перечислим основные свойства операций над множествами. Пусть U – универсальное множество, A, B, C – его подмножества, Æ – пустое множество. Равенства 1–10, 15–18 относятся к операциям объединения и пересечения; равенства 11–14 и 19–21 – к операции дополнения.
11. 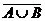
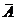
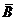
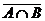
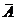
13. A È 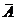
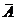
19. 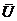
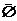
21. 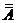
Приведем также некоторые свойства операции разности множеств: A \ B = A ∩ 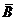
A \ Æ = A; A \ U = Æ; U \ A = 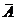
3.Разбиение множества A – такая система <Bα> непустых подмножеств множества A, что все попарные пересечения – пусты (Bi ∩ Bj = Æ, если i ≠ j – это свойство называется чистотой разбиения), а их объединение ÈBα равно A (это называется полнотой разбиения). Сами
Bα называются классами, или блоками разбиения.
При анкетировании или классификации объекты распределяются по группам; не входящие в ту или иную конкретную группу, могут составлять группировку «прочие» – для полноты разбиения.
Система курсов данного факультета есть разбиение множества его студентов; система групп есть другое разбиение того же множества. Другой пример: множество всех автомобилей может быть разными способами разбито на классы в зависимости от назначения: транспортные, специальные и гоночные; в свою очередь, транспортные автомобили подразделяются на легковые, грузовые и автобусы. Возможно разбиение в зависимости от марки, объема двигателя, года выпуска, компании-производителя, стоимости и др.
Множество квартир дома разбивается на подмножества квартир, расположенных на одном этаже; другое разбиение – на подмножества квартир из одного подъезда.
Множество R действительных чисел разбивается на множество рациональных и множество иррациональных чисел; множество Z целых чисел разбивается на множество четных и множество нечетных чисел.
Множество прямых на плоскости разбивается на бесконечную совокупность систем прямых, параллельных тому или иному направлению.
Замечание. В последнем примере элементами являются не точки плоскости, а прямые. Поэтому, например, пересечение любого множества горизонтальных прямых и любого множества вертикальных прямых пусто: ведь ни одна прямая не является одновременно горизонтальной и вертикальной.
Указание: множество M0, например, можно представить так: M0 = 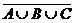
Замечание. Стоит заметить, что возможно и другое представление: M0 = 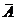
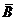
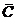
Порождающая процедура
Еще один способ задания множества связан с понятием порождающей процедуры: множество состоит из всех элементов, которые могут быть получены некоторой последовательностью операций из заданной конечной системы.
Простейший пример – задание последовательности элементов множества формулой, содержащей параметр: A = <Xk = 3 + 2(k 2 + 1)>, k = 0, 1, 2.
Задавая различные значения параметра k, мы можем вычислять элементы множества
A: X0 = 5, X1 = 7, X2 = 13 и т.д. Подобное задание может быть явным, как в данном примере, или неявным, требующим разрешения. В частности, могут использоваться возвратные, или рекуррентные соотношения, когда одни элементы множества определяются через другие.
Примеры: 1. Арифметическая прогрессия определяется заданием ее первого члена а1, разности прогрессии d и соотношением аn+1 = аn + d для n ≥ 1. Рекуррентная формула позволяет вычислять значения а2 = а1 + d, а3 = а2 + d = а1 +2d, а4 = а3 + d = а1 + 3d и т.д. Можно выразить
n-й член прогрессии в явном виде: аn = а1 + d • (n – 1).
Последняя формула позволяет последовательно вычислять значения а3 = а2 + а1 = 1 + 1 = 2,
а4 = а3 + а2 = 2 + 1 = 3, а5 = а4 + а3 = 3 + 2 = 5, а6 = а5 + а4 = 5 + 3 = 8. и т.д. Выражение общего
n-го члена этой последовательности в явном виде существует, но более сложно.
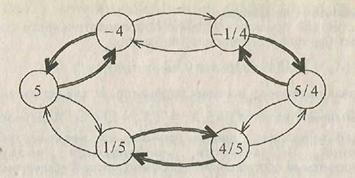
Рассмотрим еще один способ задания числового множества M:
Упражнение. Проследите, какое число в множестве М порождается, начиная с элемента 5, конечной последовательностью операций (2), (3), (3), (2), (2), (3), (2).
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Что такое пересечение множеств объединение разность
Объединение множеств X и Y — это множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств X или Y, т.е. принадлежат X или принадлежат Y.
Объединение X и Y обозначается через X∪Y
Формально x∈X∪Y ⇔ x∈X или x∈Y
Пример 3. Если X — множество точек левого круга и Y — множество точек правого круга, то
X∪Y — заштрихованная область, ограниченная обоими кругами.
представляет собой множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств данной системы М.
Для объединенных множеств справедливы:
справедливость которых вытекает из того, что левая и правая части равенств состоят из одних и тех же элементов.
Очевидно, что X∪∅ = X. Отсюда можно видеть, что ∅ играет роль нуля в алгебре множеств.
2. Пересечение множеств
Пересечение множеств X и Y — это множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству X, так и множеству Y.
Пересечение множеств обозначается X∩Y.
Формально x∈X∩Y ⇔ x∈X и x∈Y
Пример 5. Если Х — множество точек левого круга, а Y — множество точек правого круга, то X∩Y представляет собой заштрихованную область, являющуюся общей частью обоих кругов.
Множества X и Y называются непересекающимися (дизъюнктными), если они не имеют общих элементов, то есть если X∩Y=∅.
Частный случай: кортеж длины 1 —
кортеж длины 0 — или ∧ — пустой кортеж.
Отличие кортежа и обыкновенного множества: в кортеже могут быть одинаковые элементы.
Упорядоченные множества, элементами которых являются вещественные числа, будем называть векторами или точками пространства (n-мерного).
Два вектора равны, если они имеют одинаковую длину и соответствующие координаты их равны.
Компонентами кортежа (вектора) могут быть также компоненты кортежи (векторы):
Пример. Слова в предложении,
Прямое произведение множеств
Прямым (декартовым) произведением множеств X и Y называется множество, состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству X, а вторая принадлежит множеству Y.
Пример 3. Пусть X и Y — отрезки вещественной оси. Прямое произведение X*Y изображается заштрихованным прямоугольником. См. рис. б).
Прямое произведение изменяется при изменении порядка сомножителей т.е.
Очевидно X*Y = ∅ ⇔ X = ∅ или Y = ∅.
Частным случаем прямого произведения является понятие степеней (декартовых) множества — прямое произведение одинаковых множеств
M s =M*M*. *M, M 1 =M, M 0 =∧.
Обычно R — множество вещественных чисел, тогда R 2 =R*R — вещественная плоскость и R 3 =R*R*R — трехмерное вещественное пространство.
Проекция множества.
Операция программирования множества тесно связана с операцией проектирования кортежа и может применяться лишь к таким множествам, элементами которых являются кортежи одинаковой длины.
Пусть M — множество, состоящее из кортежей длины S. Тогда пролинией множества M будем называть множество пролиний всех кортежей из М
Очевидно что если М=Х*Y то Пр1М=Х, Пр2М=Y
и если Q⊆Х*Y то Пр1Q⊆Х и Пр2Q⊆Y
Пусть V — множество векторов одинаковой длины S.
В общем случае ПрiV — вовсе не обязательно прямое произведение: оно может быть подмножеством.
Операции над множествами
Пересечение множеств
Рассмотрим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = < | Том, Фред, Макс, Джорж > |
| Друзья Майкла = < | Лео, Том, Фред, Эван > |
Видим, что Том и Фред одновременно являются друзьями Джона и Майкла.
Говоря на языке множеств, элементы Том и Фред принадлежат как множеству друзей Джона, так и множеству друзей Майкла.
Зададим новое множество с названием «Общие друзья Джона и Майкла» и в качестве элементов добавим в него Тома и Фреда :
| Общие друзья Джона и Майкла | = |
В данном случае множество «Общие друзья Джона и Майкла» является пересечением множеств друзей Джона и Майкла.
Пересечением двух (или нескольких) исходных множеств называется множество, которое состоит из элементов, принадлежащих каждому из исходных множеств.
В нашем случае элементы Том и Фред принадлежат каждому из исходных множеств, а именно: множеству друзей Джона и множеству друзей Майкла.
Тогда пересечением множеств A и B будет множество C и записываться следующим образом:
Символ ∩ означает пересечение.
Говоря о множестве, обычно подразумевают элементы, принадлежащие этому множеству. Символ пересечения ∩ читается, как союз И. Тогда выражение A ∩ B = C можно прочитать следующим образом:
«Элементы, принадлежащие множеству A И множеству B, есть элементы, принадлежащие множеству C».
«Друзья, одновременно принадлежащие Джону И Майклу, есть общие друзья Джона и Майкла».
В этом случае говорят, что исходные множества не имеют общих элементов и пересечением таких множеств является пустое множество. Пустое множество обозначается символом ∅
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
Пример 4. Найти пересечение следующих множеств:
Зададим новое множество D и добавим в него элементы 3 и 9. Затем с помощью символа пересечения ∩ запишем, что пересечением множеств A, B и C является множество D
Чтобы найти пересечение, вовсе необязательно задавать множества с помощью букв. Если элементов мало, то множество можно задать прямым перечислением элементов.
Числовые промежутки, которые мы рассмотрели в предыдущих уроках, тоже являются множествами. Элементами таких множеств являются числа, входящие в числовой промежуток.
Например, отрезок [2; 6] можно понимать, как множество всех чисел от 2 до 6. Для наглядности можно перечислить все целые числа, принадлежащие данному отрезку:
Следует иметь ввиду, что мы перечислили только целые числа. Отрезку [2; 6] также принадлежат и другие числа, не являющиеся целыми, например, десятичные дроби. Десятичные дроби располагаются между целыми числами, но их количество настолько велико, что перечислить их не представляется возможным.
Еще пример. Интервал (2; 6) можно понимать, как множество всех чисел от 2 до 6, кроме чисел 2 и 6. Ранее мы говорили, что интервал это такой числовой промежуток, границы которого не принадлежат ему. Для наглядности можно перечислить все целые числа, принадлежащие интервалу (2; 6) :
Поскольку числовые промежутки являются множествами, то мы можем находить пересечения между различными числовыми промежутками. Рассмотрим несколько примеров.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [2; 6] и [4; 8] :
Тогда пересечением числовых промежутков [2; 6] и [4; 8] будет числовой промежуток [4; 6]
Пример 6. Найти пересечение числовых промежутков [−2; 3] и [4; 7]
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [−2; 3] и [4; 7] :
Видно, что числовые промежутки [−2; 3] и [4; 7] не имеют общих чисел. Поэтому их пересечением будет пустое множество:
Если изобразить числовые промежутки [−2; 3] и [4; 7] на координатной прямой, то можно увидеть, что они нигде не пересекаются:
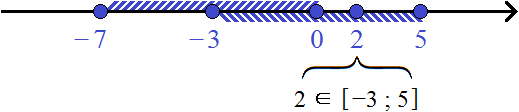
Пример 7. Дано множество из одного элемента < 2 >. Найти его пересечение с промежутком (−3; 4)
Множество, состоящее из одного элемента < 2 >, на координатной прямой изображается в виде закрашенного кружка, а числовой промежуток (−3; 4) это интервал, границы которого не принадлежат ему. Значит границы −3 и 4 будут изображаться в виде пустых кружков:
Пересечением множества < 2 >и числового промежутка (−3; 4) будет множество, состоящее из одного элемента < 2 >, поскольку элемент 2 принадлежит как множеству < 2 >, так и числовому промежутку (−3; 4)
На самом деле мы уже занимались пересечением числовых промежутков, когда решали системы линейных неравенств. Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
По сути, множество решений, удовлетворяющих обоим неравенствам, является пересечением множеств решений первого и второго неравенства. Роль этих множеств берут на себя числовые промежутки.
Например, чтобы решить систему неравенств 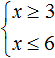
В данном примере решением первого неравенства x ≥ 3 является множество всех чисел, которые больше 3 (включая само число 3). Иначе говоря, решением неравенства является числовой промежуток [3; +∞)
Решением второго неравенства x ≤ 6 является множество всех чисел, которые меньше 6 (включая само число 6). Иначе говоря, решением неравенства является числовой промежуток (−∞; 6]
А общим решением системы будет пересечение множеств решений первого и второго неравенства, то есть пересечение числовых промежутков [3; +∞) и (−∞; 6]
Поэтому в качестве ответа мы указывали, что значения переменной x принадлежат числовому промежутку [3; 6], то есть пересечению множеств решений первого и второго неравенства
Пример 2. Решить неравенство
Все неравенства, входящие в систему уже решены. Нужно только указать те решения, которые являются общими для всех неравенств.
Запишем ответ к системе 
Пример 3. Решить неравенство
В данном случае пересечением числовых промежутков (7; +∞) и (−∞; 4) является пустое множество, поскольку эти числовые промежутки не имеют общих элементов:
Если изобразить числовые промежутки (7; +∞) и (−∞; 4) на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Объединение множеств
Объединением двух (или нескольких) исходных множеств называют множество, которое состоит из элементов, принадлежащих хотя бы одному из исходных множеств.
На практике объединение множеств состоит из всех элементов, принадлежащих исходным множествам. Поэтому и говорят, что элементы такого множества принадлежат хотя бы одному из исходных множеств.
Рассмотрим множество A с элементами 1, 2, 3 и множество B с элементами 4, 5, 6.
Зададим новое множество C и добавим в него все элементы множества A и все элементы множества B
В данном случае объединением множеств A и B является множество C и обозначается следующим образом:
Символ ∪ означает объединение и заменяет собой союз ИЛИ. Тогда выражение A ∪ B = C можно прочитать так:
Элементы, принадлежащие множеству A ИЛИ множеству B, есть элементы, принадлежащие множеству C.
В определении объединения сказано, что элементы такого множества принадлежат хотя бы одному из исходных множеств. Данную фразу можно понимать в прямом смысле.
Если мы захотим объединить два или более множества и вдруг обнаружим, что один или несколько элементов принадлежат каждому из этих множеств, то в объединение повторяющиеся элементы будут входить только один раз.
Например, рассмотрим множество A с элементами 1, 2, 3, 4 и множество B с элементами 2, 4, 5, 6.
Итак, у нас имеются следующие исходные множества:
Зададим новое множество С и добавим в него все элементы множества A
Пример 2. Друзьями Джона являются Том, Фред, Макс и Джордж. А друзьями Майкла являются Лео, Том, Фред и Эван. Найти объединение множеств друзей Джона и Майкла.
Для начала зададим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = < | Том, Фред, Макс, Джорж > |
| Друзья Майкла = < | Лео, Том, Фред, Эван > |
Зададим новое множество с названием «Все друзья Джона и Майкла» и добавим в него всех друзей Джона и Майкла.
Заметим, что Том и Фред одновременно являются друзьями Джона и Майкла, поэтому мы добавим их в новое множество только один раз, поскольку сразу двух Томов и двух Фредов не бывает.
| Все друзья Джона и Майкла | = |
В данном случае множество всех друзей Джона и Майкла является объединением множеств друзей Джона и Майкла.
Друзья Джона ∪ Друзья Майкла = Все друзья Джона и Майкла
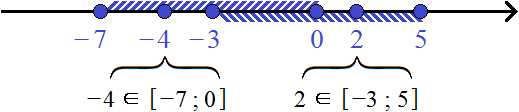
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие этим промежуткам:
−7, −6, −5, −4, −3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−7; 5]
Обратите внимание, что числа −3,−2, −1 принадлежали и первому промежутку и второму. Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.
Значит объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5]
Не каждое объединение числовых промежутков является числовым промежутком. Например, попробуем найти объединение числовых промежутков [−2 ; −1] и [4 ; 7].
Числовой промежуток должен содержать все числа от левой границы до правой. Если одно из чисел отсутствует, то числовой промежуток теряет смысл. Допустим, имеется линейка длиной 15 см
Эта линейка является числовым промежутком [0; 15], поскольку содержит все числа в промежутке от 0 до 15 включительно. Теперь представим, что на линейке после числа 9 сразу следует число 12.
Решение неравенств, содержащих знак ≠
Подставим, например, число 5
5 ≠ 4 — верное неравенство, поскольку 5 не равно 4
7 ≠ 4 — верное неравенство, поскольку 7 не равно 4
Изобразим множество решений неравенства x ≠ 4 на координатной прямой. Для этого выколем точку 4 на координатной прямой, а всю оставшуюся область с обеих сторон выделим штрихами:
Пример 2. Решить неравенство 3x − 5 ≠ 1 − 2x
Перенесем −2x из правой части в левую часть, изменив знак, а −5 из левой части перенесём в правую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 5
Изобразим множество решений неравенства x ≠ 1,2 на координатной прямой и запишем ответ в виде числового промежутка:
В этом выражении говорится, что значения, принимаемые переменной x принадлежат промежутку (−∞; 1,2) или промежутку (1,2; +∞)
Решение совокупностей неравенств
Рассмотрим ещё один вид неравенств, который называется совокупностью неравенств. Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.
Совокупность неравенств очень похожа на систему неравенств. Различие в том, что в системе неравенств нужно найти множество решений, удовлетворяющих каждому неравенству, образующему эту систему.
А в случае с совокупностью неравенств, нужно найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность.
Совокупность неравенств обозначается квадратной скобкой. Например, следующая запись из двух неравенств является совокупностью:
Решим данную совокупность. Сначала нужно решить каждое неравенство по отдельности.
Например, число 9 из промежутка [3; +∞) удовлетворяет первому неравенству x ≥ 3. А число −7 из промежутка (−∞; 6] удовлетворяет второму неравенству x ≤ 6.
Стало быть, решением совокупности неравенств является объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности 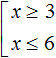
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
Возьмём любое число из полученного объединения, и проверим удовлетворяет ли оно хотя бы одному неравенству.
Возьмем для примера число 8. Оно удовлетворяет первому неравенству x ≥ 3.
Возьмем еще какое-нибудь число, например, число 1. Оно удовлетворяет второму неравенству x ≤ 6
Пример 2. Решить совокупность неравенств
Чтобы решить эту совокупность, нужно найти множество решений, которые удовлетворяют хотя бы одному неравенству, образующему эту совокупность.
Множеством решений второго неравенства x ≥ −7 является числовой промежуток [−7; +∞).
Решением совокупности неравенств 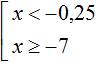
Иначе говоря, решением совокупности 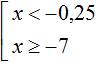
Объединением числовых промежутков (−∞; −0,25) и [−7; +∞) является является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
Ответ можно оставить таким, каким мы его записали ранее:
либо заменить на более короткий:
Пример 3. Решить совокупность неравенств
Решим каждое неравенство по отдельности:
Решением совокупности неравенств 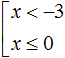
Иначе говоря, решением совокупности 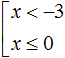
Объединением числовых промежутков (−∞; −3) и (−∞; 0] является числовой промежуток (−∞; 0]
Ответ можно оставить таким, каким мы его записали ранее: