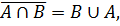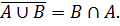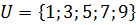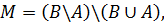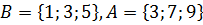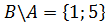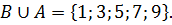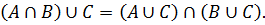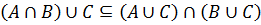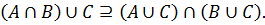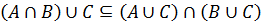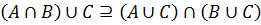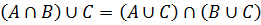Что такое пересечение множеств

Пересечение и объединение множеств — свойства, операции и примеры решения

Математика часто оперирует абстрактными объектами, для задания связи между которыми существуют различные операции, такие как пересечение и объединение множеств.

Понятие множества является интуитивным, не определяемым. Оно обычно ассоциируется с набором чего-либо, группой каких-то предметов или живых объектов, совокупностью некоторых условий, рассматривается как класс, семейство в некоторой классификации, промежуток числовой прямой. Например, в геометрии рассматриваются линии как множества точек.

То, из чего состоит множество, называется его элементами.

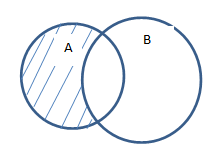
Графическим изображением, служащим для наглядности рассматриваемых объектов, является круг Эйлера.

Что такое пересечение множеств

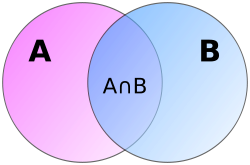
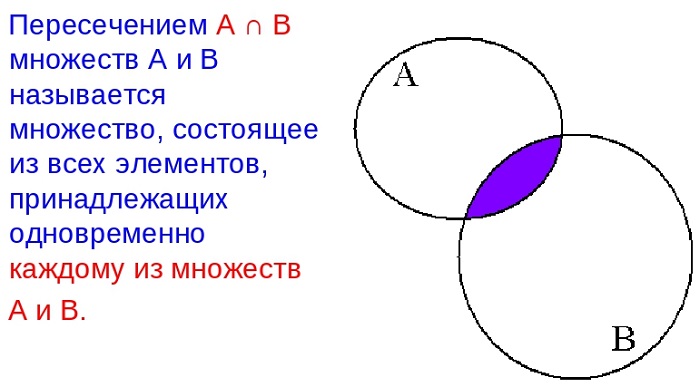
Для любого набора множеств их пересечением называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из заданных. Другими словами, это совокупность всех общих элементов.

С помощью кругов Эйлера-Венна пересечение можно изобразить так:

Часто применяется для определения решений систем уравнений и неравенств.

Ассоциируется с обычным умножением двух числовых объектов.

Что такое объединение множеств

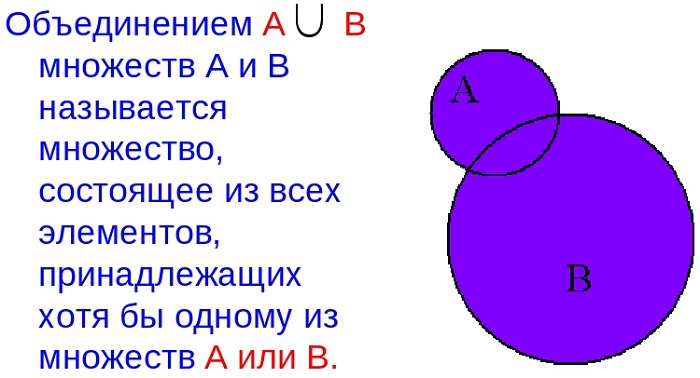
Для любого набора множеств, их объединением называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных.

Изображение кругами Эйлера выглядит следующим образом:

Часто используется при решении уравнений и неравенств, подчёркивая наличие серий корней и решений, нескольких используемых промежутков числовой прямой.

В обычной математике близко по смыслу с операцией, называемой «сложение».

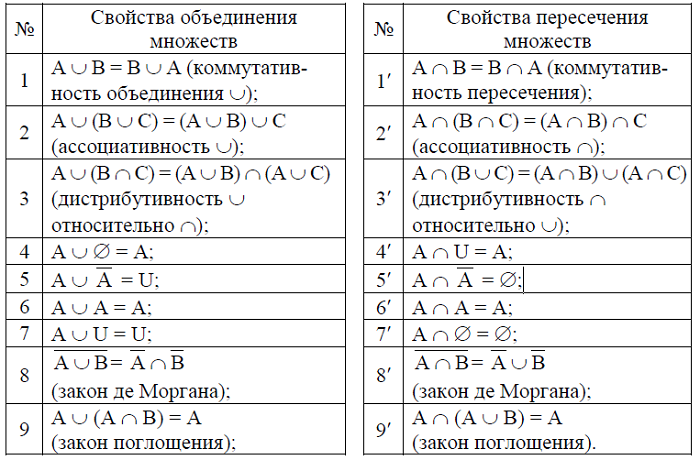
Свойства пересечения и объединения множеств

Для решения задач нужно знать о следующих свойствах:

1. Коммутативность (перестановочность):

Эти свойства распространяются на любое количество компонентов. Следуют из определения операций.

2. Ассоциативность (расстановка скобок):

Данные свойства также применимы к большому количеству компонентов. Позволяют опускать скобки и упрощать запись.

3. Дистрибутивность (раскрытие скобок):

(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C);

(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C).

4. Закон идемпотентности (идентичности):

Множество, не содержащее ни одного элемента, называется пустым. Обозначается перечёркнутым нулём: Ø

Выполнение операций с Ø:

Прослеживается аналог со сложением и умножением на ноль.

Операции над множествами

Помимо объединения и пересечения существуют другие операции:

Для двух множеств A и B можно определить их разность как набор элементов, входящих в A и не содержащихся в B:

Рассматривая некоторое множество в качестве содержащего все остальные, можно прийти к понятию «дополнение», как к совокупности всех элементов, не входящих в A:

Благодаря этой операции свойства объединения и пересечения можно расширить/

Примеры решения задач

Задача №1

Выписать все элементы множества

При поиске M операции выполняются последовательно.

B A состоит из всех элементов B, которые не принадлежат A, поэтому:

B ∪ A включает в себя все элементы, принадлежащие хотя бы одному из множеств A или B. Таким образом:

M = (B A) (B ∪ A) состоит из всех элементов B A, которые не принадлежат B ∪ A, следовательно, M = Ø.

Задача №2

Доказать методом включений тождество:

Необходимо доказать выполнение включений:

Выбирается произвольный x из (A ∩ B) ∪ C. По определению операции объединения x ∈ B ∩ A или x ∈ C.

Если x ∈ B ∩ A, то по определению пересечения x ∈ B и x ∈ A.

Так как x ∈ A, то x ∈ C ∪ A; так как x ∈ B, то x ∈ C ∪ B, следовательно, x ∈ (A ∪ C) ∩ (B ∪ C).

Если x ∈ C, то x ∈ C ∪ A и x ∈ C ∪ B, а значит: x ∈ (A ∪ C) ∩ (B ∪ C).

Поскольку x ∈ (A ∩ B) ∪ C был выбран произвольно, утверждается, что любой элемент этого множества содержится в (A ∪ C) ∩ (B ∪ C), то есть:

Выбирается произвольный y из (A ∪ C) ∩ (B ∪ C).

По определению операции пересечения y ∈ C ∪ A и y ∈ C ∪ B.

Так как y ∈ C ∪ A, то y ∈ A или y ∈ C; так как y ∈ C ∪ B, то y ∈ C или y ∈ B. Таким образом, y ∈ C или y ∈ A и y ∈ B.

Если y ∈ A и y ∈ B, то y ∈ B ∩ A, а, следовательно, y ∈ (A ∩ B) ∪ C; если y ∈ C, то также y ∈ (A ∩ B) ∪ C.

Поскольку y из (A ∪ C) ∩ (B ∪ C) выбирался произвольно, утверждается, что любой элемент этого множества содержится в (A ∩ B) ∪ C, то есть

Из пунктов 1 и 2 вытекает, что

Источник

Пересечение множеств

Пересече́ние мно́жеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

Содержание

Определение

Пусть даны два множества и . Тогда их пересечением называется множество

Замечание

Гораздо реже используется обозначение .

Свойства

Пример

Пусть Тогда

Примечания

См. также

Полезное

Смотреть что такое «Пересечение множеств» в других словарях:

ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ — понятие теории множеств; пересечение множеств множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам. Пересечение множеств А и В обозначают А?В или АВ … Большой Энциклопедический словарь

пересечение множеств — понятие теории множеств; пересечение множеств множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам. Пересечение множеств А и В обозначают А∩В или АВ. * * * ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ … Энциклопедический словарь

Пересечение множеств — множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам. П. м. A и B обозначают A∩B или AB; П. м. Ak, взятых в конечном или бесконечном числе, обозначают Ak. П. м. может быть пустым, то есть не… … Большая советская энциклопедия

ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ — понятие теории множеств; П. м. множество, состоящее из всех тех элементов, к рые принадлежат одноврем. всем данным множествам. П. м … Естествознание. Энциклопедический словарь

Пересечение (теория множеств) — Пересечение A и B Пересечение множеств в теории множеств это множество, состоящее из элементов, которые принадлежат одновременно всем данным множествам. Содержание 1 Определение 2 Замечание … Википедия

МНОЖЕСТВ ТЕОРИЯ — раздел математики, в котором изучаются общие свойства множеств, преимущественно бесконечных. понятие множества простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек … Большой Энциклопедический словарь

множеств теория — раздел математики, в котором изучаются общие свойства множеств, преимущественно бесконечных. Понятие множества простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество… … Энциклопедический словарь

множеств теория — математическая теория, изучающая точными средствами проблему бесконечности. Предмет М. л. свойства множеств (совокупностей, классов, ансамблей), гл. обр. бесконечных. Множество A есть любое собрание определенных и различимых между собой объектов … Словарь терминов логики

Множеств теория — Теория множеств раздел математики, в котором изучаются общие свойства множеств. Теория множеств лежит в основе большинства математических дисциплин; она оказала глубокое влияние на понимание предмета самой математики. Содержание 1 Теория… … Википедия

МНОЖЕСТВ ТЕОРИЯ — раздел математики, в к ром изучаются общие свойства множеств, преим. бесконечных. Понятие множества простейшее матем. понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек на прямой… … Естествознание. Энциклопедический словарь

Источник

Пересечение и объединение множеств

Вы будете перенаправлены на Автор24

В результате математических операций над множествами из исходных множеств получается новое множество, причем этот результат однозначен. Примерами таких операций являются пересечение и объединение множеств. Эти операции производятся по определенным правилам, о которых пойдет речь ниже.

Объединение двух множеств представляет собой совокупность таких элементов, что каждый из них является элементом одного из исходных множеств. Пересечение же множеств состоит из всех элементов, общих для исходных множеств.

Обозначения множеств. Знаки объединения и пересечения множеств

В такой форме объединение записывается как

Для графического выражения операций пересечения и объединения применяются знаки пересечения и объединения множеств:

Готовые работы на аналогичную тему

Правила нахождения пересечений и объединений

Правила для нахождения пересечений и объединений множеств заключаются в следующем:

Для нахождения пересечения нескольких конечных множеств, нужно перебрать числа первого из них и выяснить, принадлежит ли текущий элемент каждому из рассматриваемых множеств. Если это условие не соблюдается, он не принадлежит пересечению. В качестве проверочного (элементы которого перебираются) следует выбирать множество с наименьшим числом элементов.

$A \cap B \cap C \cap D = \<1, 2\>$.

Исследование множеств с помощью координатной прямой

С помощью координатной прямой удобно анализировать пересечения и объединения множеств. Они изображаются друг под другом на координатных прямых с совпадающими точками и направлениями отсчета. Для отображения объединения множеств координатные прямые отмечают слева квадратной скобкой, для обозначения пересечения используется фигурная скобка.

Для решения применим графический метод:

Рисунок 1. Графическое решение задачи. Автор24 — интернет-биржа студенческих работ

Ответ:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 05 03 2021

Источник

Что такое пересечение множеств

Объединение множеств X и Y — это множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств X или Y, т.е. принадлежат X или принадлежат Y.

Объединение X и Y обозначается через X∪Y

Формально x∈X∪Y ⇔ x∈X или x∈Y

Пример 3. Если X — множество точек левого круга и Y — множество точек правого круга, то

X∪Y — заштрихованная область, ограниченная обоими кругами.

представляет собой множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств данной системы М.

Для объединенных множеств справедливы:

справедливость которых вытекает из того, что левая и правая части равенств состоят из одних и тех же элементов.

Очевидно, что X∪∅ = X. Отсюда можно видеть, что ∅ играет роль нуля в алгебре множеств.

2. Пересечение множеств

Пересечение множеств X и Y — это множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству X, так и множеству Y.

Пересечение множеств обозначается X∩Y.

Формально x∈X∩Y ⇔ x∈X и x∈Y

Пример 5. Если Х — множество точек левого круга, а Y — множество точек правого круга, то X∩Y представляет собой заштрихованную область, являющуюся общей частью обоих кругов.

Множества X и Y называются непересекающимися (дизъюнктными), если они не имеют общих элементов, то есть если X∩Y=∅.

Частный случай: кортеж длины 1 —

кортеж длины 0 — или ∧ — пустой кортеж.

Отличие кортежа и обыкновенного множества: в кортеже могут быть одинаковые элементы.

Упорядоченные множества, элементами которых являются вещественные числа, будем называть векторами или точками пространства (n-мерного).

Два вектора равны, если они имеют одинаковую длину и соответствующие координаты их равны.

Компонентами кортежа (вектора) могут быть также компоненты кортежи (векторы):

Пример. Слова в предложении,

Прямое произведение множеств

Прямым (декартовым) произведением множеств X и Y называется множество, состоящее из всех тех и только тех упорядоченных пар, первая компонента которых принадлежит множеству X, а вторая принадлежит множеству Y.

Пример 3. Пусть X и Y — отрезки вещественной оси. Прямое произведение X*Y изображается заштрихованным прямоугольником. См. рис. б).

Прямое произведение изменяется при изменении порядка сомножителей т.е.

Очевидно X*Y = ∅ ⇔ X = ∅ или Y = ∅.

Частным случаем прямого произведения является понятие степеней (декартовых) множества — прямое произведение одинаковых множеств

M s =M*M*. *M, M 1 =M, M 0 =∧.

Обычно R — множество вещественных чисел, тогда R 2 =R*R — вещественная плоскость и R 3 =R*R*R — трехмерное вещественное пространство.

Проекция множества.

Операция программирования множества тесно связана с операцией проектирования кортежа и может применяться лишь к таким множествам, элементами которых являются кортежи одинаковой длины.

Пусть M — множество, состоящее из кортежей длины S. Тогда пролинией множества M будем называть множество пролиний всех кортежей из М

Очевидно что если М=Х*Y то Пр₁М=Х, Пр₂М=Y

и если Q⊆Х*Y то Пр₁Q⊆Х и Пр₂Q⊆Y

Пусть V — множество векторов одинаковой длины S.

В общем случае Пр_iV — вовсе не обязательно прямое произведение: оно может быть подмножеством.

Источник

Математика часто оперирует абстрактными объектами, для задания связи между которыми существуют различные операции, такие как пересечение и объединение множеств. Понятие множества является интуитивным, не определяемым. Оно обычно ассоциируется с набором чего-либо, группой каких-то предметов или живых объектов, совокупностью некоторых условий, рассматривается как класс, семейство в некоторой классификации, промежуток числовой прямой. Например, в геометрии рассматриваются линии как множества точек.

То, из чего состоит множество, называется его элементами.

Графическим изображением, служащим для наглядности рассматриваемых объектов, является круг Эйлера.

Что такое пересечение множеств

Для любого набора множеств их пересечением называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из заданных. Другими словами, это совокупность всех общих элементов.

С помощью кругов Эйлера-Венна пересечение можно изобразить так:

Часто применяется для определения решений систем уравнений и неравенств.

Ассоциируется с обычным умножением двух числовых объектов.

Что такое объединение множеств

Изображение кругами Эйлера выглядит следующим образом:

Часто используется при решении уравнений и неравенств, подчёркивая наличие серий корней и решений, нескольких используемых промежутков числовой прямой.

В обычной математике близко по смыслу с операцией, называемой «сложение».

Свойства пересечения и объединения множеств

Для решения задач нужно знать о следующих свойствах:

1. Коммутативность (перестановочность):

Эти свойства распространяются на любое количество компонентов. Следуют из определения операций.

2. Ассоциативность (расстановка скобок):

Данные свойства также применимы к большому количеству компонентов. Позволяют опускать скобки и упрощать запись.

3. Дистрибутивность (раскрытие скобок):

(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C);

(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C).

4. Закон идемпотентности (идентичности):

Множество, не содержащее ни одного элемента, называется пустым. Обозначается перечёркнутым нулём: Ø

Выполнение операций с Ø:

Прослеживается аналог со сложением и умножением на ноль.

Операции над множествами

Помимо объединения и пересечения существуют другие операции:

Для двух множеств A и B можно определить их разность как набор элементов, входящих в A и не содержащихся в B:

Рассматривая некоторое множество в качестве содержащего все остальные, можно прийти к понятию «дополнение», как к совокупности всех элементов, не входящих в A:

Благодаря этой операции свойства объединения и пересечения можно расширить/

Примеры решения задач

Задача №1

Выписать все элементы множества

При поиске M операции выполняются последовательно.

B \ A состоит из всех элементов B, которые не принадлежат A, поэтому:

B ∪ A включает в себя все элементы, принадлежащие хотя бы одному из множеств A или B. Таким образом:

M = (B \ A) \ (B ∪ A) состоит из всех элементов B \ A, которые не принадлежат B ∪ A, следовательно, M = Ø.

Задача №2

Доказать методом включений тождество:

Необходимо доказать выполнение включений:

Выбирается произвольный x из (A ∩ B) ∪ C. По определению операции объединения x ∈ B ∩ A или x ∈ C.

Если x ∈ B ∩ A, то по определению пересечения x ∈ B и x ∈ A.

Так как x ∈ A, то x ∈ C ∪ A; так как x ∈ B, то x ∈ C ∪ B, следовательно, x ∈ (A ∪ C) ∩ (B ∪ C).

Если x ∈ C, то x ∈ C ∪ A и x ∈ C ∪ B, а значит: x ∈ (A ∪ C) ∩ (B ∪ C).

Поскольку x ∈ (A ∩ B) ∪ C был выбран произвольно, утверждается, что любой элемент этого множества содержится в (A ∪ C) ∩ (B ∪ C), то есть:

Выбирается произвольный y из (A ∪ C) ∩ (B ∪ C).

По определению операции пересечения y ∈ C ∪ A и y ∈ C ∪ B.

Так как y ∈ C ∪ A, то y ∈ A или y ∈ C; так как y ∈ C ∪ B, то y ∈ C или y ∈ B. Таким образом, y ∈ C или y ∈ A и y ∈ B.

Если y ∈ A и y ∈ B, то y ∈ B ∩ A, а, следовательно, y ∈ (A ∩ B) ∪ C; если y ∈ C, то также y ∈ (A ∩ B) ∪ C.

Поскольку y из (A ∪ C) ∩ (B ∪ C) выбирался произвольно, утверждается, что любой элемент этого множества содержится в (A ∩ B) ∪ C, то есть

Из пунктов 1 и 2 вытекает, что

Источник