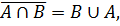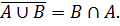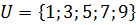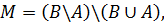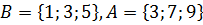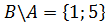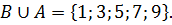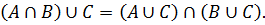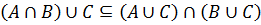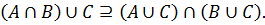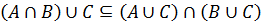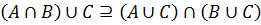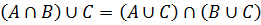Что такое пересечение в математике 5 класс

Точка и линия

Я не буду рассказывать вам, что об этом пишут в различных учебниках, ведь вы здесь для того, чтобы понять и применять, а не для того, чтобы зубрить. Я расскажу так, чтобы было понятно.

Точка – это воображаемый геометрический объект, не имеющий никаких размеров и не состоящий ни из чего.
У точки нет ни длины, ни ширины, ни высоты. Ее нельзя измерить. Точка неделимая. Она не состоит ни из каких-либо других частей.

Зачем нужна точка, если она воображаемая? Для чего ее придумали?

Точка выполняет только одну задачу: указание месторасположения.

Пример: точка на карте навигатора указывает нам на то, где находится конечный пункт поездки, то есть, на его местоположение.

Линия – это множество точек, расположенных последовательно друг за другом.

Например, представим себе цепь. Можно вообразить, что каждое ее звено – это точка. И точно так же, как цепь состоит из звеньев, соединенных между собой, так и линия состоит из точек, образно говоря, склеенных друг с другом.

Рис. 1 Цепь и линия

Линия не имеет ширины и высоты, но можно измерить ее длину. Линия состоит из точек.

Как можно измерить то, что состоит из придуманных объектов, не имеющих размеров? Зачем нужна линия?

Действительно, геометрическая точка не имеет размеров, ее невозможно измерить. Но она, как было сказано выше, указывает на местоположение чего-либо конкретного.

Возьмем для примера опять навигатор. Вы на автомобиле проехали от своего дома в любимое кафе.

Рис. 2 Путь автомобиля

Можем ли мы представить автомобиль точкой? Да, можем. Во время движения автомобиль изменял свое местоположение. Чтобы показать на карте, в каких именно местах побывал автомобиль во время поездки, мы обозначим их точками, следовательно, для упрощения рисунка мы смело можем заменить автомобиль точкой. Тогда полный путь от дома к кафе (множество мест на дороге, на которых побывала машина) мы можем изобразить в виде линии, то есть, идущих друг за другом точек. А так как путь от дома к кафе имеет какую-то длину, то и нарисованная линия имеет длину, равную этому пути, а значит, линию можно измерить.

Рис. 3 Контур и диапазон

Как видно на примере рисунка 3-а, при помощи линии обозначено очертание птицы на ветке, а на 3-б – пример решения неравенств методом интервалов.

Для чего нужна линия:
1. Показывает путь движения какого-либо объекта;
2. С ее помощью можно измерить расстояние между какими-нибудь объектами;
3. Служит для обозначения границ объекта или фигуры;
4. Показывает диапазон каких-то значений.

Обозначение точек и линий

Рис. 4 Обозначение точек и линий

Взаимное расположение точек и линии

Точка может принадлежать линии (то есть, быть одной из ее составляющих), а может не принадлежать ей.

Рис. 4.1 Принадлежность точек линии

При записи на письме точка обозначается при помощи знака точка, заключенного в скобки, с добавлением заглавной буквы латинского алфавита: (·) H

Теперь я запишу то, что мы увидели на рисунке 4.1, на языке геометрии, а вы попробуйте прочитать самостоятельно:

Виды линий

Рис. 5 Замкнутая и незамкнутая линия

Замкнутая линия не имеет обрывающихся концов. Она начинается и заканчивается в одной точке. Причем эта точка может находиться в любом месте на этой линии.

Рис. 6 Контур птицы

Незамкнутая линия имеет один или два обрывающихся конца. Начало и конец такой линии находятся в разных местах (точки A и B ).

Рис. 7 Незамкнутые линии

Еще несколько примеров.

1. Ты вышел из дома погулять и вернулся домой. Какой линией можно обозначить твой путь? Правильно, замкнутой.

2. Ты вышел из дома, погулял, а потом зашел к соседу. Какой линией можно обозначить твой путь? Правильно, разомкнутой.

3. Ты вышел из дома и пошел к другу в дом напротив. Какой линией можно обозначить твой путь? Правильно, разомкнутой.

Также линии бывают:

Рис. 11 Самопересекающиеся и не самопересекающиеся линии

Попробуйте сформулировать самостоятельно, какие линии называются самопересекающиеся, а какие – не самопересекающиеся.

Рис. 12 Прямая, ломаная, кривая линии

Более подробно о прямых, кривых и ломаных линиях рассмотрено в других уроках.

Источник

Плоскость, прямая линия, луч

Плоскость в математике можно сравнить с другими плоскостями, которые окружают нас в повседневной жизни: школьная доска, лист бумаги, экран планшета или смартфона и т.д. На них мы можем легко обозначить точки и линии, которые мы изучали на предыдущем уроке. На школьной доске мы это делаем мелом или фломастером, на листе бумаги можем нарисовать их ручкой, карандашом, фломастером; когда мы прокручиваем окно сайта или приложения на смартфоне, мы проводим на экране пальцем линию, когда переходим по ссылкам – ставим на его плоскости точку.

Но эти примеры плоскостей из жизни имеют свои размеры и границы, они конечные, их можно измерять.

Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной.

Плоскость нельзя измерять, потому что она бесконечная.

Плоскость нельзя согнуть, в каком бы положении она ни находилась.

Все объекты и фигуры, которые изучаются в курсе математики 5 класса, находятся на плоскости.

Прямая линия

Прямая линия – абсолютно ровная линия, которая длится бесконечно в обе стороны, и на всем ее протяжении не изгибается и не преломляется.

Обозначение прямой

Например, на рисунке 1 обозначены такие прямые:

Рис. 1 Обозначение прямой линии

Рис. 2 Обозначение прямой с несколькими точками

Некоторые свойства прямой

Две точки, лежащие на одной прямой, создают отрезок этой прямой.

Через две любые точки на плоскости можно провести единственную прямую.

Рис. 3 Отрезок на прямой

Две разные прямые могут пересекаться или не пересекаться.

Две прямые пересекаются в том случае, если у них есть общая точка.

Рис. 5 Пересечение прямых

Более подробно об этих и других свойствах прямой написано в уроке геометрии 7 класса.

Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону.

Рис. 6 Деление прямой линии точкой

У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.

Свое название этот математический объект получил по аналогии с лучом света, который имеет начало (источник света), но определенного конца у него нет.

Обозначение луча

Луч, как и прямую, обозначают двумя способами.

Рис. 7 Обозначение луча

На рисунке 2 приведены примеры обозначения луча:

Луч имеет второе название – полупрямая.

Рис. 8 Дополнительные друг другу и совпадающие лучи

На рисунке 8 видно, что:

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.6 / 5. Количество оценок: 22

Источник

Математика. 5 класс

Конспект урока

Прямая, луч, отрезок

Перечень рассматриваемых вопросов:

— понятия «прямая», «луч», «отрезок»;

— отличия прямой, луча, отрезка;

— прямая, луч, отрезок на чертежах, рисунках и моделях.

Отрезок – часть прямой, ограниченный двумя точками.

Концы отрезка – точки, ограничивающие отрезок.

Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.

Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).

Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.

Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.

Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.

Через любые две точки можно провести только одну прямую.

Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.

Провести через точки А и В другую прямую, отличную от прямой b, нельзя.

Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.

Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.

Каждую из этих частей называют лучом, исходящим из точки А.

Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.

Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.

Переставлять буквы в названии луча нельзя.

Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.

Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.

В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.

Заметим, что два отрезка называются равными, если они совмещаются при наложении.

Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.

Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.

Разбор решения заданий тренировочного модуля

№ 1. Тип задания: добавление подписей к изображениям.

Разместите нужные подписи к изображениям.

Для выполнения задания обратитесь к теоретическому материалу урока.

№ 2. Тип задания: подстановка элементов в пропуски в тексте.

Вставьте в текст нужные слова.

Через__________ две____________ можно провести только одну _________.

Слова: любые; точки; прямую; ломаную.

Правильный ответ: через любые две точки можно провести только одну прямую.

Источник

Математика часто оперирует абстрактными объектами, для задания связи между которыми существуют различные операции, такие как пересечение и объединение множеств. Понятие множества является интуитивным, не определяемым. Оно обычно ассоциируется с набором чего-либо, группой каких-то предметов или живых объектов, совокупностью некоторых условий, рассматривается как класс, семейство в некоторой классификации, промежуток числовой прямой. Например, в геометрии рассматриваются линии как множества точек.

То, из чего состоит множество, называется его элементами.

Графическим изображением, служащим для наглядности рассматриваемых объектов, является круг Эйлера.

Что такое пересечение множеств

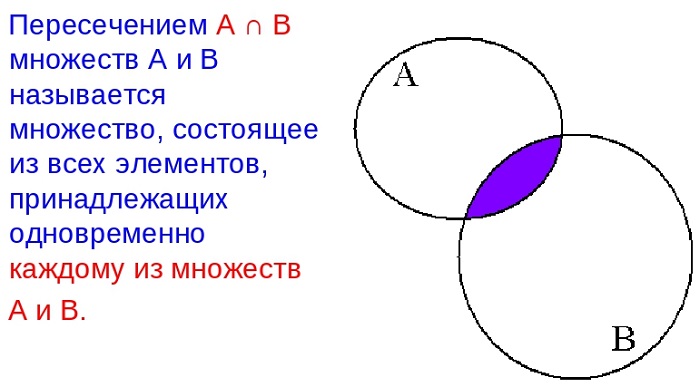
Для любого набора множеств их пересечением называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из заданных. Другими словами, это совокупность всех общих элементов.

С помощью кругов Эйлера-Венна пересечение можно изобразить так:

Часто применяется для определения решений систем уравнений и неравенств.

Ассоциируется с обычным умножением двух числовых объектов.

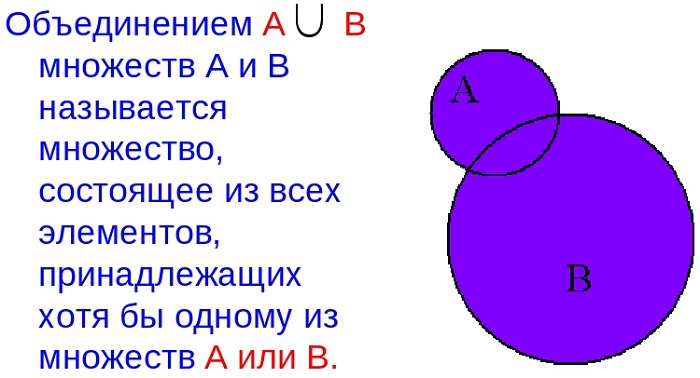
Что такое объединение множеств

Изображение кругами Эйлера выглядит следующим образом:

Часто используется при решении уравнений и неравенств, подчёркивая наличие серий корней и решений, нескольких используемых промежутков числовой прямой.

В обычной математике близко по смыслу с операцией, называемой «сложение».

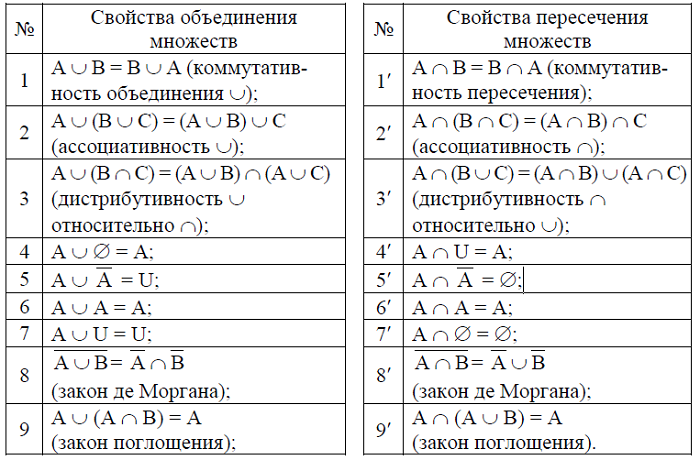
Свойства пересечения и объединения множеств

Для решения задач нужно знать о следующих свойствах:

1. Коммутативность (перестановочность):

Эти свойства распространяются на любое количество компонентов. Следуют из определения операций.

2. Ассоциативность (расстановка скобок):

Данные свойства также применимы к большому количеству компонентов. Позволяют опускать скобки и упрощать запись.

3. Дистрибутивность (раскрытие скобок):

(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C);

(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C).

4. Закон идемпотентности (идентичности):

Множество, не содержащее ни одного элемента, называется пустым. Обозначается перечёркнутым нулём: Ø

Выполнение операций с Ø:

Прослеживается аналог со сложением и умножением на ноль.

Операции над множествами

Помимо объединения и пересечения существуют другие операции:

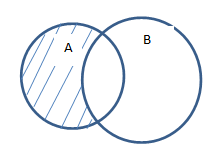
Для двух множеств A и B можно определить их разность как набор элементов, входящих в A и не содержащихся в B:

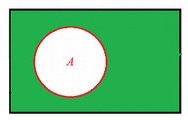
Рассматривая некоторое множество в качестве содержащего все остальные, можно прийти к понятию «дополнение», как к совокупности всех элементов, не входящих в A:

Благодаря этой операции свойства объединения и пересечения можно расширить/

Примеры решения задач

Задача №1

Выписать все элементы множества

При поиске M операции выполняются последовательно.

B \ A состоит из всех элементов B, которые не принадлежат A, поэтому:

B ∪ A включает в себя все элементы, принадлежащие хотя бы одному из множеств A или B. Таким образом:

M = (B \ A) \ (B ∪ A) состоит из всех элементов B \ A, которые не принадлежат B ∪ A, следовательно, M = Ø.

Задача №2

Доказать методом включений тождество:

Необходимо доказать выполнение включений:

Выбирается произвольный x из (A ∩ B) ∪ C. По определению операции объединения x ∈ B ∩ A или x ∈ C.

Если x ∈ B ∩ A, то по определению пересечения x ∈ B и x ∈ A.

Так как x ∈ A, то x ∈ C ∪ A; так как x ∈ B, то x ∈ C ∪ B, следовательно, x ∈ (A ∪ C) ∩ (B ∪ C).

Если x ∈ C, то x ∈ C ∪ A и x ∈ C ∪ B, а значит: x ∈ (A ∪ C) ∩ (B ∪ C).

Поскольку x ∈ (A ∩ B) ∪ C был выбран произвольно, утверждается, что любой элемент этого множества содержится в (A ∪ C) ∩ (B ∪ C), то есть:

Выбирается произвольный y из (A ∪ C) ∩ (B ∪ C).

По определению операции пересечения y ∈ C ∪ A и y ∈ C ∪ B.

Так как y ∈ C ∪ A, то y ∈ A или y ∈ C; так как y ∈ C ∪ B, то y ∈ C или y ∈ B. Таким образом, y ∈ C или y ∈ A и y ∈ B.

Если y ∈ A и y ∈ B, то y ∈ B ∩ A, а, следовательно, y ∈ (A ∩ B) ∪ C; если y ∈ C, то также y ∈ (A ∩ B) ∪ C.

Поскольку y из (A ∪ C) ∩ (B ∪ C) выбирался произвольно, утверждается, что любой элемент этого множества содержится в (A ∩ B) ∪ C, то есть

Из пунктов 1 и 2 вытекает, что

Источник

Урок «Пересечение и объединение множеств»

Разделы: Математика

Цели урока:

Ход урока.

1. Организационный момент.

2. Учитель сообщает тему урока, совместно с учащимися формулирует цели и задачи.

3. Учитель совместно с учащимися вспоминает материал, изученный по теме «Множества» в 7 классе, вводит новые понятия и определения, формулы для решения задач.

«Множество есть многое, мыслимое нами как единое» (основатель теории множеств – Георг Кантор). КАНТОР (Cantor) Георг (1845—1918) — немецкий математик, логик, теолог, создатель теории трансфинитных (бесконечных) множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв.

К сожалению, основному понятию теории – понятию множества – нельзя дать строгого определения. Разумеется, можно сказать, что множество – это «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «система», «класс» и т. д. однако всё это было бы не математическим определением, а скорее злоупотреблением словарным богатством русского языка.

Для того чтобы определить какое – либо понятие, нужно, прежде всего, указать, частным случаем какого более общего понятия, оно является, для понятия множества сделать это невозможно, потому что более общего понятия, чем множество, в математике нет.

Часто приходится говорить о нескольких вещах, объединенных некоторым признаком. Так, можно говорить о множестве всех стульев в комнате, о множестве всех клеток человеческого тела, о множестве всех картофелин в данном мешке, о множестве всех рыб в океане, о множестве всех квадратов на плоскости, о множестве всех точек на данной окружности т. д.

Предметы, составляющие данное множество, называются его элементами.

Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.

Множество месяцев – из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.

Например, если А означает множество всех натуральных чисел, то 6 принадлежит к А, а 3 не принадлежит к А.

Если множество содержит конечное число элементов, то его называют конечным, а если в нем бесконечно много элементов, то бесконечным. Так множество деревьев в лесу конечно, а множество точек на окружности бесконечно.

Парадокс в логике — это противоречие, имеющее статус логически корректного вывода и, вместе с тем, представляющее собой рассуждение, приводящее к взаимно исключающим заключениям.

Как уже упоминалось, понятие множества лежит в основе математики. Используя простейшие множества и различные математические конструкции, можно построить практически любой математический объект. Идею построения всей математики на основе теории множеств активно пропагандировал Г.Кантор. Однако, при всей своей простоте, понятие множества таит в себе опасность появления противоречий или, как ещё говорят, парадоксов. Появление парадоксов связано с тем, что далеко не всякие конструкции и не всякие множества можно рассматривать.

Одному солдату было приказано брить тех и только тех солдат его взвода, которые сами себя не бреют. Неисполнение приказа в армии, как известно, тягчайшее преступление. Однако возник вопрос, брить ли этому солдату самого себя. Если он побреется, то его следует отнести к множеству солдат, которые сами себя бреют, а таких брить он не имеет права. Если же он себя брить не будет, то попадёт во множество солдат, которые сами себя не бреют, а таких солдат согласно приказу он обязан брить. Парадокс.

Сравнение множеств.

Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент В:

В этом случае A называется подмножеством B, B — надмножеством A. Если , то A называется собственным подмножеством В. Заметим, что ,

По определению ,

Два множества называются равными, если они являются подмножествами друг друга

Операции над множествами

Пересечение.

Объединение.

Свойства.

1.Операция объединения множеств коммутативна

2.Операция объединения множеств транзитивна

3. Пустое множество X является нейтральным элементом операции объединения множеств

1. Пусть A = <1,2,3,4>,B = <3,4,5,6,7>. Тогда

2. А=<2,4,6,8,10>, В = <3,6,9,12>. Найдём объединение и пересечение этих множеств:

<2,4,6,8, 10,3,6,9,12>, = <6>.

3. Множество детей является подмножеством всего населения

4. Пересечением множества целых чисел с множеством положительных чисел является множество натуральных чисел.

5. Объединением множества рациональных чисел с множеством иррациональных чисел является множество положительных чисел.

6.Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.

Диаграммы Венна (Venn diagrams) — общее название целого ряда методов визуализации и способов графической иллюстрации, широко используемых в различных областях науки и математики: теория множеств, собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства; разновидностями диаграмм Венна служат: диаграммы Эйлера,

Диаграмма Венна четырёх множеств.

Собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства. Обычная диаграмма Венна имеет три множества. Сам Венн пытался найти изящный способ с симметричными фигурами, представляющий на диаграмме большее число множеств, но он смог это сделать только для четырех множеств (см. рисунок справа), используя эллипсы.

Диаграммы Эйлера

Диаграммы Эйлера аналогичны диаграммам Венна. Диаграммы Эйлера можно использовать, для того, чтобы оценивать правдоподобность теоретико-множественных тождеств.

Задача 1. В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?

Все они умеют танцевать, т.к. по условию каждый ученик класса поёт или танцует. Всего умеют танцевать 19 человек, из них 13 не умеют петь, значит, танцевать и петь одновременно умеют 19-13 = 6 человек.

Задачи на пересечение и объединение множеств.

Источник