Что такое пересекающиеся прямые 7 класс

Пересекающиеся прямые

Пересекающиеся прямые — это в евклидовой геометрии пересечение двух прямых может быть пустым множеством, точкой или прямой. Различение этих случаев и поиск точки пересечения используется, например, в компьютерной графике, при планировании движения и для обнаружения столкновений.

Содержание:

Понятие пересекающихся прямых

Определение. Если две прямые имеют только одну общую точку, то такие прямые называют пересекающимися.

На рисунке 2.291 прямые пересекаются в точке О.

Можно доказать такую теорему.

Теорема 1. Через две пересекающиеся прямые можно провести плоскость, и только одну.

Несколько прямых могут пересекаться не в одной точке, а, например, попарно. На рисунке 2.292 изображено пересечение трех прямых, каждые две из которых пересекаются только в одной точке. При этом образуется треугольник и вся эта фигура всегда лежит в одной плоскости.

Четыре прямые, каждые две из которых имеют только одну общую точку, образуют четырехугольник (рис. 2.293).

На рисунках 2.294, 2.295 изображены куб и тетраэдр, у которых продолжены их ребра. Мы видим, что в каждой вершине куба и тетраэдра пересекаются три прямые.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Геометрия 7 класс.
Точка, прямая и отрезок

Казалось бы, что таким простым понятиям, как «точка» или «прямая», которые мы повседневно используем в жизни, крайне просто дать определения. Но на практике оказалось, что это не так.

Существует множество определений, которые давали знаменитые математики терминам «точка» и «прямая». За многие века ученые так и не пришли к единому определению.

Мы не будем приводить все определения точки и прямой. Остановимся на объяснениях, которые, на наш взгляд, наиболее простым образом их описывают.

Точка — элементарная фигура, не имеющая частей.

Прямая состоит из множества точек и простирается бесконечно в обе стороны.

То есть выражаясь геометрическими обозначениями, информацию о расположении прямой и точек на рисунке выше можно записать так:

Как обозначить прямую

Прямую обычно обозначают одной маленькой латинской буквой.

Прямую, на которой отмечены две точки, иногда обозначают по названиям этих точек большими латинскими точками.

Задача № 1 из учебника Атанасян 7-9 класс

Решение задачи

Опишем взаимное расположение точек и прямой.

Как обозначается пересечение прямых

Хотя на чертеже не видно, но прямые a и c тоже пересекаются (это становится ясно, если мысленно продолжить вниз прямые a и с ).

Прямые e и f не имеют общей точки — т.е. они не пересекаются.

Взаимное расположение прямой и точек

Через одну точку (·)A можно провести сколько угодно прямых.

Через две точки (·)A и (·)B можно провести только одну прямую.

Сколько общих точек имеют две прямые

Две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Докажем утверждение выше. Для этого рассмотрим все возможные случаи расположения двух прямых.

Первый случай расположения прямых

На рисунке выше мы видим, что у прямых f и e нет общих точек, т.к. эти прямые не пересекаются.

Второй случай расположения прямых

Третий случай расположения прямых

Вывод: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Задача № 3 из учебника Атанасян 7-9 класс

Проведите три прямые так, чтобы каждые две из них пересекались. Обозначьте все точки пересечения этих прямых. Сколько получилось точек? Рассмотрите все возможные случаи.

Решение задачи

Проведём две прямые a и b так, чтобы эти две прямые пересекались, и обозначим точку пересечения.

Как мы видим, точка пересечения только одна. Мы можем провести третью прямую так, чтобы она тоже проходила через эту точку пересечения.

Мы убедились, что возможны оба варианта. Поэтому в ответе запишем их оба.

Ответ: точек пересечения получается одна или три.

Что такое отрезок

Отрезок — часть прямой, ограниченная двумя точками.

В отличии от прямой любой отрезок можно измерить. Т.е. каждый отрезок имеет длину.

Источник

Пересекающиеся прямые

Если две прямые имеют общую точку, то говорят, что эти прямые пересекаются. Такие прямые называют пересекающимися прямыми:

Точка пересечения — это точка, общая для двух или более геометрических фигур.

Перпендикуляр и наклонная

При пересечении вертикальной и горизонтальной прямой линии образуется четыре прямых угла. Такие линии, относительно друг к другу, называются перпендикулярными линиями или просто перпендикулярами:

Даже если прямые не являются вертикальной и горизонтальной линиями, но при пересечении образуют четыре прямых угла, то они всё равно являются перпендикулярными:

Если прямая линия пересекает другую не под прямым углом, то такая линия называется наклонной к прямой, которую она пересекает. При этом образуется четыре угла: два из них будут острыми и два тупыми:

Образованные острые углы равны и относительно друг друга будут называться вертикальными углами. То же самое можно сказать и об образованных тупых углах — они равные и вертикальные.

Источник

Пересечение прямых. Точка пересечения двух прямых

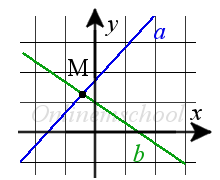
Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.

Точка пересечения двух прямых на плоскости

Если система уравнений:

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

Вычтем из первого уравнения второе

Из первого уравнения найдем значение x

Подставим значение x во второе уравнение и найдем значение y

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

В первое уравнение подставим значения x и y из второго и третьего уравнений.

Подставим значение t во второе и третье уравнение

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

Из второго уравнения выразим y через x

Подставим y в первое уравнение

Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k ₁ = k ₂ = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.

Решим также эту задачу используя систему уравнений:

Вычтем из первого уравнения второе

Ответ. Прямые не пересекаются (прямые параллельны).

Решение: Подставим координаты точки N в уравнения прямых.

Точка пересечения двух прямых в пространстве

Если система уравнений:

Решение: Составим систему уравнений

К шестому уравнению добавим пятое уравнение

Подставим значение b в четвертое и пятое уравнения

x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1

Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).

Решение: Составим систему уравнений заменив во втором уравнении параметр t на a

Подставим значение t из шестого уравнения в остальные уравнения

Источник

Геометрия Тема урока: Пересекающиеся прямые. Параллельные прямые, 7Б

Класс: 7А, 7Б Геометрия

Тема урока: Пересекающиеся прямые. Параллельные прямые

Цели: ввести понятие параллельных прямых; рассмотреть признак параллельности двух прямых, связанный с накрест лежащими углами.

I. Организационный момент.

II. Объяснение нового материала.

1. Повторить возможные случаи взаимного расположения двух прямых на плоскости, используя при этом готовые чертежи.

2. Предложить учащимся провести обоснование того факта, что две прямые не могут иметь двух или более общих точек.

3. Дать определение параллельных прямых и соответствующее обозначение: а | | b.

4. Ввести понятие параллельных отрезков, отрезка и прямой, луча и прямой, отрезка и луча, двух лучей по рисунку 99 учебника.

5. Ввести понятие секущей по отношению к двум прямым по рисунку 100.

6. Рассмотреть и ввести название различных пар углов, образованных двумя прямыми и секущей: накрест лежащие углы, односторонние углы, соответственные углы (рис. 100).

7. По заранее заготовленным таблицам или рисункам на доске провести работу:

1) По рисунку 1 назовите пары накрест лежащих, односторонних, соответственных углов.

2) На рисунке 2 4 = 6.

Докажите, что 5 = 3; 8 = 6; 2 = 5.

3) На рисунке 3 1 = 5:

а) выпишите все пары накрест лежащих углов и докажите, что в каждой паре углы равны;

б) выпишите все пары соответственных углов и докажите, что в каждой паре углы равны;

в) выпишите все пары односторонних углов и докажите, что сумма углов в каждой паре равна 180°.

8. Повторить признаки равенства треугольников и утверждение о том, что две прямые, перпендикулярные к третьей, не пересекаются
(п. 12).

9. Вспомнить еще раз определение параллельных прямых и отметить, что так как прямые бесконечны, то невозможно непосредственно убедиться в том, что они не имеют общей точки. Поэтому желательно иметь какие-то признаки, по которым можно сделать вывод о параллельности прямых. С понятием «признак» мы уже встречались, когда изучали признаки равенства треугольников. Теперь же предстоит познакомиться с признаками параллельности двух прямых.

III. Работа с учебником.

1. Проведение по тексту учебника доказательства теоремы – признака параллельности двух прямых, использующего накрест лежащие углы (рис. 101).

Это доказательство не является традиционным – во многих учебниках этот признак доказывается методом от противного.

В процессе доказательства необходимо акцентировать внимание учащихся на назначении дополнительных построений (рис. 101, в учебника).

2. Теорема является важной и сама по себе, и потому, что на нее опираются доказательства других признаков параллельности прямых.

3. Устно решить задачу № 187 (рис. 107) и задачу № 189 (по рис. 108 или по ранее заготовленным плакатам).

IV. Закрепление изученного материала.

1. Задача. Найти пары параллельных прямых (отрезков) и доказать их параллельность (по готовым чертежам на доске (см. рис. 1–3):

2. Решить задачу № 191 на доске и в тетрадях учащихся.

Дано: АВС; ВK – биссектриса.

Докажите, что KМ | | АВ.

По условию ВМ = МK, тогда треугольник ВМK – равнобедренный (по определению), значит, МВK = МKВ (углы при основании равнобедренного треугольника равны). По условию ВK – биссектриса В, то МВK = АВK.

Следовательно, АВK = МВK = МKВ, а АВK и МKВ – накрест лежащие углы, тогда АВ | | KМ.

Домашнее задание: изучить пункты 24–25 (только первый признак); решить задачи №№ 186, 188.

Тема урока: Решение прямоугольных треугольников.

Цели: Умение находить решения прямоугольных треугольников.

2. Новый материал. По каким основным элементам можно построить прямоугольные треугольник? [4 случая] Объясните, почему каждая из таких задач на построение имеет единственное решение. [Признаки равенства прямоугольных треугольников] Следовательно, зная те же пары основных элементов в прямоугольном треугольнике, можно однозначно вычислить остальные его элементы. Такие вычислительные задачи называют решением прямоугольных треугольников, то есть, решить прямоугольный треугольник – это значит: по двум данным его основным элементам вычислить остальные.

Рассмотрим решение прямоугольных треугольников в общем виде. На доске и в тетрадях: рис. 1 и записи.

Какие еще возможны способы вычислений в каждом из случаев? Почему лучше пользоваться записанными способами? [Точность приближенных вычислений]

3. Упражнения (письменно на доске и в тетрадях без чертежа и записи условий):

П.: стр. 95, №45 (2г и 4г)

[2г) b = 13; sin   0,9882;   81  12`;   8  48`; 4г)  = 22  ; с  9,7; b  3,6]

4. Практические задачи (самостоятельно в тетрадях с устной проверкой):

1) Найдите угол наклона прямолинейной дороги, если на каждые 200 метров пути приходится 6 метров спуска по вертикали. [sin  = 0,03;   1  43`]

2) Тень от вертикального шеста, имеющего длину 7 метров, составляет 4 метра. Найдите угол высоты солнца над горизонтом. [tg  = 1,75;   60  15`]

Домашнее задание: решение прямоугольных треугольников – по тетради; П.: стр. 95, №45 (1г; 3г); №37 (приближенно); п. 44 (стр. 89-90) – прочитайте самостоятельно вычисление точных значений тригонометрических функций углов 45  ; 30  и 60  и выучите эти значения.

Докажите, что треугольник является равносторонним т. и т. т., когда сумма длин любой его стороны и проведенной к ней высоты есть одно и то же число.

Класс: 5 Математика

Тема урока: Сложение смешанных чисел.

Цели: показать применение переместительного и сочетательного свойства сложения при сложении смешанных чисел; ввести правило сложения смешанных чисел, применять данное правило при нахождении значений выражений, решении задач и уравнений; развивать умение работать самостоятельно с учебником.

I. Организационный момент

1. Найдите значение выражения:

2. Представьте дробную часть чисел в виде неправильной дроби, уменьшив целую часть этих чисел на 1:

3. Выделите целую часть из чисел:

IV . Сообщение темы урока

— Сегодня на уроке мы познакомимся с алгоритмом сложения смешанных чисел.

V. Изучение нового материала

1. Подготовительная работа.

— Назовите смешанные числа:

— Почему эти числа так называются?

— Представьте смешанные числа в виде суммы их целой и дробной частей.

— Запишите переместительное свойство сложения в буквенном виде.

— Запишите сочетательное свойство сложения в буквенном виде.

(а + b ) + с = а + ( b + с)

— Приведите примеры на применение этих свойств при сложении дробей. Эти свойства позволяют складывать смешанные числа.

2. Работа над новой темой.

а) Сложите числа:

— Расскажите, как складываются смешанные числа, когда дробные части имеют одинаковые знаменатели. (Сначала складывают целые части, затем — дробные части.)

— Какие свойства сложения были использованы? (Сочетательное и переместительное.)

б) Сложите числа:

— Что делать, когда дробные части смешанных чисел имеют разные знаменатели?

(По ходу ответов учащихся учитель на доске может записать памятку сложения смешанных чисел, затем эту памятку дети записывают в тетрадь).

3. Работа с учебником, стр. 59 (в парах).

— Рассмотрите в учебнике пример 1.

— Как поступить в том случае, когда дробная часть 101/60 представлена неправильной дробью? (Выделишь целую часть.)

4. Работа с учебником, стр. 60 (в парах).

— Рассмотрите в учебнике пример 2.

— Прочитайте правило сложения смешанных чисел.

— Расскажите это правило товарищу.

— Приведите свои примеры, аналогичные примерам 1 и 2 учебника.

VI. Закрепление изученного материала

№ 376 стр. 61 (с подробным комментированием у доски и в тетрадях, первые два примера записать подробно, потом короче).

(Ответы: .)

VIII. Работа над задачей

1. № 382 стр. 62 (у доски ученик во время разбора задачи записывает решение).

— Прочитайте задачу. Что известно? Что надо узнать?

— Давайте решим задачу с вопросами по действиям.

— Примем за единицу весь бассейн.

— Зная, что весь бассейн это — 1, или целое, и что первая труба, работая отдельно, заполняет его за 4 ч, первым действием можно узнать, какую часть бассейна заполняет первая труба за 1 ч.

Какую часть бассейна заполняет первая труба за 1 ч? 1/4 (часть)

Какую часть бассейна заполняет вторая труба за 1 ч? 1/6 (часть)

Какую часть бассейна заполняют обе трубы за 1 ч, работая одновременно?

(частей бассейна.)

Какую часть бассейна останется наполнить после 1 ч совместной работы двух труб?

(частей бассейна.)

(Ответ: 7/12 частей бассейна.)

2. № 389 стр. 63 (один ученик на обратной стороне доски, остальные — самостоятельно, самопроверка).

— Что такое периметр треугольника?

(Ответ: периметр треугольника — )

IX. Самостоятельная работа

Вариант I. № 408 (1 строчка) стр. 65.

X. Подведение итогов урока

— На каких свойствах сложения основано сложение смешанных чисел.

— Расскажите алгоритм сложения смешанных чисел.

Источник