Что такое периметр 3 класс

Периметр

Периметр — это сумма длин всех сторон многоугольника.

Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.

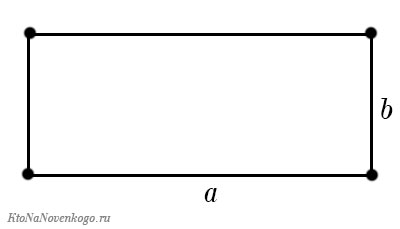
Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.

AB = 3 см, BC = 7 см

P_ABCD = (AB + BC) · 2
P_ABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

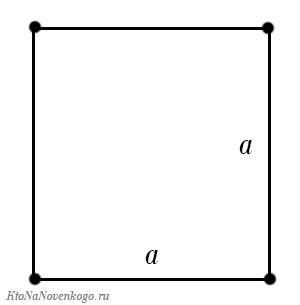
Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».

KE = 7 см

P_EKFM = 4 · KE
P_EKFM = 4 · 7 = 28 (см)

Как найти периметр многоугольника

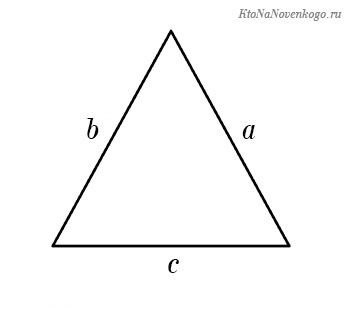
Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

P_ABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Источник

Как найти периметр треугольника

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

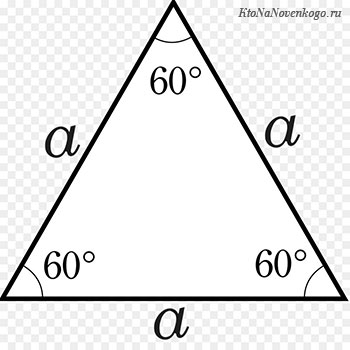
Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

Гипотенуза — сторона, которая лежит напротив прямого угла.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Источник

Периметр и площадь прямоугольника

Прямоугольники и квадраты обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D

Определения:

Прямоугольник – это четырёхугольник, у которого все углы прямые.

Квадрат – это прямоугольник, у которого стороны равны. Его называют правильным четырёхугольником.

Периметр прямоугольника – это сумма длин всех сторон прямоугольника.

Формулы

Дан прямоугольник ABCD.

Периметр равен сумме длин сторон.

P_ABCD = AB + BC + CD + AD

Противоположные стороны прямоугольника равны.

P_ABCD = 2 * AB + 2 * BC = 2 * (AB + BC)

Следовательно, для того, чтобы высчитать периметр прямоугольника, нужно сложить длины двух сторон и умножить результат на 2.

У квадрата все стороны равны.

Поэтому, периметр квадрата равен:

Площадь прямоугольника равна произведению длины на ширину.

Определить площадь, периметр, объем, длину, диаметр, высоту и остальные геометрические величины поможет онлайн-калькулятор https://max-calc.ru.

На сайте вы сможете не только получить готовое решение, но и посмотреть всю необходимую справочную информацию.

Задачи:

1. Хозяин дачи решил построить забор вокруг участка. Какой длины получится забор, если участок имеет вид прямоугольника с шириной 15 метров и длиной 33 метра?

Для нахождения длины забора нужно посчитать периметр участка.

Воспользуемся формулай Р_{участка} = 2 * (длина + ширина).

Р _{участка} = 2 * (15 м + 33 м) = 96 м

Ответ: длина забора 96 метров.

2. Мама решила пришить на скатерть красивую тесьму. Сколько нужно купить тесьмы, если скатерть квадратная со стороной 150 сантиметров?

Так как скатерть квадратная, для определения длины тесьмы нужно найти периметр квадрата.

Р = 4 * 150 см = 600 см = 6 м

Ответ: нужно купить 6 метров тесьмы.

3. Известно, что банки краски хватает, чтобы покрасить 30 м 2 поверхности. Хватит ли одной банки краски, чтобы покрасить забор длиной 15 метров и высотой 2 метра?

Для решения необходимо найти площадь поверхности забора. Для этого длину умножаем на ширину.

S_забора = 15 м * 2 м = 30 м2.

Ответ: да, 1 банки краски хватит.

Задачи для самостоятельной работы:

1. Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Уважаемые читатели!

Все материалы с сайта можно скачивать абсолютно бесплатно. Все материалы проверены антивирусом и не содержат скрытых скриптов.

Материалы в архиве не помечены водяными знаками!

Если материал нарушает чьи-то авторские права, просьба написать нам по обратной связи, указав авторство материала. Мы обязуемся либо убрать материал, либо указать прямую ссылку на автора.

Сайт пополняется материалами на основе бесплатной работы авторов. Eсли вы хотите отблагодарить их за работу и поддержать наш проект, вы можете перевести любую, не обременительную для вас сумму на счет сайта.
Заранее Вам спасибо.

Источник

Периметр – это границы измерений

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.

Сегодня мы подробно расскажем, что такое ПЕРИМЕТР, как он считается и каково его практическое применение.

Материал этот изучают в начальных классах школы, но далеко не всегда получается понятно объяснить простые вещи.

Что такое периметр

Периметр – это общая граница любой плоской геометрической фигуры. Измеряется в тех же величинах, что и стороны многоугольников.

У окружности тоже есть периметр. Хотя само слово в этом случае не применяют, говоря – длина окружности. Интересно, что само слово ПЕРИМЕТР изначально и обозначало окружность.

Так оно переводится с древнегреческого «περίμετρον». Но другой, более общий перевод – «измеряю вокруг», и тогда он подходит под все плоские геометрические фигуры как окружность, так и многоугольники.

Расчет периметра многоугольников

Считать периметр многоугольников очень просто. Надо всего лишь сложить длины всех сторон. И неважно, насколько замысловато выглядят сами фигуры.

Рассмотрим периметры самых популярных фигур.

Периметр треугольника

Как мы уже сказали, для расчета периметра треугольника надо просто сложить все его стороны.

Периметр обозначается латинской буквой «P». Он будет равен:

А если треугольник равносторонний или как его еще называют – правильный, то формула заметно упрощается.

Периметр прямоугольника

Отличительная черта прямоугольника – его противоположные стороны равны.

P = a + b + a + b = 2a + 2b = 2 (a + b)

Как и у треугольника, у прямоугольника есть частный случай, когда всего его стороны равны между собой. И всем известно, что называется такая фигура – квадрат.

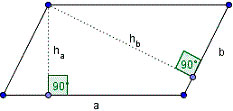
Периметр параллелограмма

Если кто забыл, то параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны между собой.

И периметр у него считается точно так же, как и у прямоугольника. Более того, прямоугольник – это частный случай параллелограмма.

P = a + a + b + b = 2a + 2b = 2 (a + b)

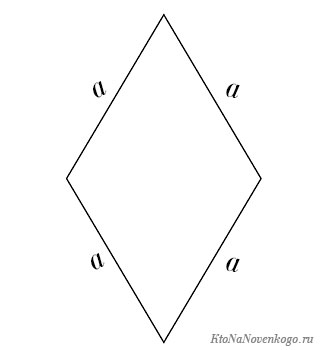
У параллелограмма есть еще один частный случай. Фигура, у которой все стороны равны. И называется она – ромб.

Его периметр считается точно так же, как и у квадрата.

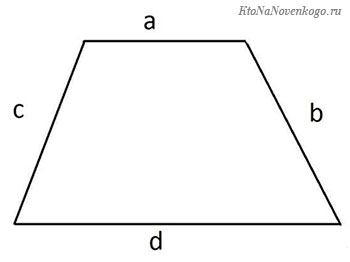
Периметр трапеции

И еще одна фигура, которая частенько встречается в жизни. И ее изучению посвящены отдельные главы школьной программы. Трапеция – это четырехугольник, у которого только две стороны лежат на параллельных прямых.

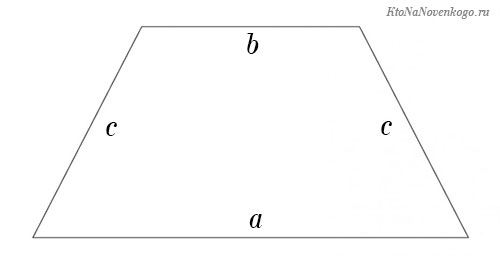
Но есть и частный случай, который называется равнобедренной трапецией. У этой фигуры непараллельные стороны равны между собой и идут под одинаковым наклоном.

P = a + b + c + c = a + b + 2c

Расчет длины окружности

Для расчета длины окружности, которая, по сути, и является периметром фигуры, есть своя формула. Вот только эту величину, в отличие от многоугольников, принято обозначать латинской буквой «L».

В этой формуле букой r обозначается радиус окружности, то есть расстояние от ее центра до границы. А буква π – это математическая постоянная, которая равна 3,14 (хотя на самом деле число знаков после запятой бесконечно).

Вместо заключения

Для чего в жизни нужно знать про ПЕРИМЕТР? Приведем самый простой пример.

Если вы на даче соберетесь поставить забор, вам нужно будет точно знать, сколько материала покупать. Для этого вы измерите свой участок по длине и ширине. Как правило, дачные участки имеют форму прямоугольников. Соответственно, после этого легко будет посчитать периметр:

где L – длина участка, а W – ширина. И уже с этими расчетами вы можете смело ехать в строительный магазин.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Не только это. Термин «периметр» весьма распространен в силовых структурах. Например: «Прапорщик Савельев отвечает за охрану периметра А, сержант Николаев — за периметр Б». То есть — какой-то ограниченный сектор с особым режимом, находящийся под сигнализацией и т.д.

Источник

Как найти периметр фигуры

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение периметра

Периметр — это сумма длин всех сторон многоугольника.

Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.

Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.

Формулы нахождения периметра

Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.

Равносторонний многоугольник

У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.

Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.

А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.

Прямоугольник и параллелограмм

У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.

P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

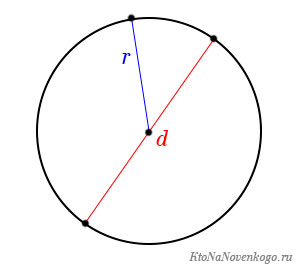
Окружность

У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.

L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

Ответ: две другие стороны равны по 17 см.

Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.

Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!

Источник