Что такое периметр многоугольника 3 класс правило примеры

Периметр многоугольника

Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.

В математике периметр обозначают буквой P (пэ).

Периметр прямоугольника

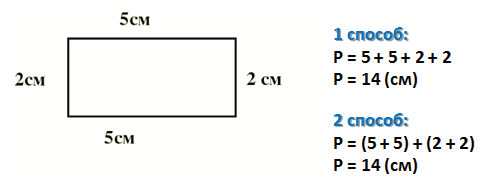
Например, найдём периметр данного прямоугольника.

Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.

Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.

Формула для подсчета периметра прямоугольника:

(a + b) • 2

a – длина прямоугольника

b – ширина прямоугольника.

Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.

Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:

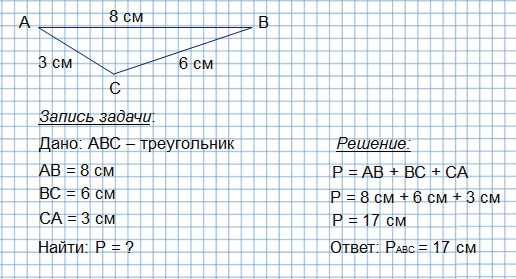
Периметр треугольника

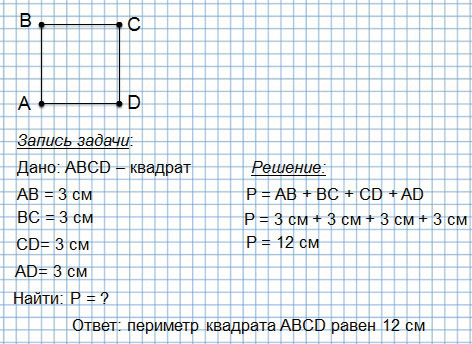
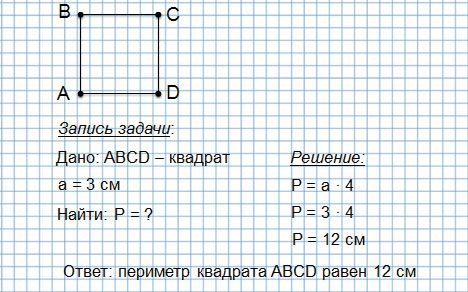
Периметр квадрата

Первый способ (когда мы еще не знаем действие умножения):

Второй способ (когда мы изучили действие умножения):

Поделись с друзьями в социальных сетях:

Источник

Что такое периметр и площадь

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Как вычислить периметр

Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a*4

P= a+a+a+a

Например, перед нами квадрат со стороной 10 см.

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S= a*a

S=a 2

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.

Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

S= a*b

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L= 2πd

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.

Источник

Тема урока «Периметр многоугольников». 3-й класс

Класс: 3

Презентация к уроку

Дидактическая цель: обеспечить усвоение детьми различных способов нахождения периметра многоугольников и научить выбирать рациональные.

1. Организационный момент.

2. Актуализация знаний.

Учитель: Сегодня необычный урок – урок – исследования. Попробуем применить накопленные знания для открытия новых. Чтобы узнать какое математическое понятие является объектом исследования, надо отгадать зашифрованное имя литературного героя.

1) Найдите частное чисел 49 и 7. (7)

Учитель: Назовите фигуру, под которой написано это число?

2) Произведение 40, первый множитель 5. Найдите второй множитель. (8)

Учитель: Назовите фигуру, под которой написано это число?

3) Частное чисел 18, делитель 3. Найдите делимое. (6)

Учитель: Назовите фигуру, под которой написано это число?

6) 24 уменьшить в 8 раз. (3)

Учитель: Назовите фигуру, под которой написано это число?

Учитель: На следующей строчке запишите числа в порядке возрастания.

Проверка: 3, 6, 7, 8, 9

Учитель: Под каждой цифрой напишите букву и назовите слово.

Учитель: Из какого произведения эта необычная девочка?

Дети: Льюис Кэрролл “Алиса в стране чудес”, “Алиса в Зазеркалье”.

— Я, думаю, длину всей геометрической фигуры.

— Я согласен. А длина геометрической фигуры называктся периметром.

Учитель: Назовите тему урока.

Дети: Периметр геометрических фигур.

Запись в тетради и на доске: Периметр

Учитель: Нам знакома эта тема? (Да)

(Дети проверяют собственные нания по данной теме.)

Учитель: Составим план нашей исследовательской работы.

Ученики распределяют этапы урока.

5. Повторение и систематизация знаний по теме.

а) Понятие “периметр”. (1 ступень на лестнице)

Учитель: Что такое периметр?

Периметр – сумма длин всех сторон геометрических фигур.

б) Единицы измерения.

Учитель: Какими единицами измеряется периметр?

Дети: Единицами длины: км, м, дм, см, мм.

в) Периметр треугольника. (2 ступень лестницы.)

Учитель: Следующая ступень – способы нахождения периметра разных геометрических фигур. Посмотрите на доску. Назовите геометрические фигуры, у которых наименьшее количество углов.

Учитель: Назовите существенные признаки треугольников.

Дети: 3угла, 3 стороны.

Учитель: Под каким номером треугольники?

Учитель: Найдите периметр треугольников.

Сам. работа. (Работа парами.)

Проверка. (3 человека у доски)

Учитель: Где сумму можно заменить умножением?

(2 ученика работают у доски.)

1 ученик

(№8) Р = 2 +2 +2 = 6(см) 2 3 = 6 (см)

2 ученик

(№9) Р = 3 + 3 + 1 = 7(см) 3 2 + 1 = 7 (см)

Учитель: Чем треугольники отличаются?

Дети: У первого – все стороны одинаковые, у второго – две стороны одинаковые, а третья имеет другую длину, у третьего – все стороны имеют разную длину.

Учитель: Алиса обозначила каждую сторону треугольников буквами. Определите, какая формула подходит к каждому виду треугольников.

Вывод. Периметр треугольника можно найти умножением, если стороны одинаковые.

(Учитель на доску помещает таблицу с формулами.)

Р = а + в + с

Р = а x 3

Р = а x 2 + в

г) Периметр прямоугольника. (2 ступень лестницы.)

Учитель: Назовите фигуры, у которых на один угол больше.

Учитель: Назовите признаки четырехугольников.

Дети: 4 угла, 4 стороны.

Учитель: Как называется четырёхугольники под номером № 7?

Учитель: Назовите существенные признаки прямоугольников.

Дети: Все углы прямые.

Учитель: Какое свойство прямоугольников мы знаем?

Дети: У прямоугольников противоположные стороны равны.

Учитель: Найдите периметр прямоугольника 3 способами.

Сам. работа. (Работа парами.)

Учитель: Какие из трёх способов рациональные?

Учитель: Алиса стороны прямоугольника обозначила буквами. Запишем формулы ко 2 и 3 способам.

(Проверяется на слайде. Учитель на доску помещает таблицу с формулами.)

д) Периметр квадрата. (2 ступень лестницы.)

Учитель: Найти ещё один прямоугольник.

Учитель: Как называется такой прямоугольник?

Учитель: Назовите существенные признаки квадрата.

Дети: Все стороны равны.

Учитель: Найдите периметр квадрата 2 способами.

Сам. работа. (Работа парами.)

Учитель: Какой из двух способов рациональный?

Учитель: Сторону квадрата Алиса обозначила буквой. Запишите формулу.

(1 ученик записывает формулу на доске.)

(Проверяется на слайде. Учитель на доску помещает таблицу с формулами.)

Учитель: Сделайте вывод. Какой способ нахождения периметра многоугольника рациональный?

Вывод. Если у геометрической фигуры стороны равны, то можно сложение заменить умножением, т.е. использовать рациональный способ вычисления.

Учитель: Алиса измеряла периметр пятиугольников. Она обозначили стороны буквами и написали формулы. Вот что у неё получилось. Соедините формулу нахождения периметра с изображением фигуры.

7. Самостоятельная работа.

— Сегодня на уроке я узнал.

Источник

Как найти периметр фигуры

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение периметра

Периметр — это сумма длин всех сторон многоугольника.

Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.

Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.

Формулы нахождения периметра

Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.

Равносторонний многоугольник

У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.

Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.

А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.

Прямоугольник и параллелограмм

У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.

P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Окружность

У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.

L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

Ответ: две другие стороны равны по 17 см.

Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.

Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!

Источник

Формула расчета периметра многоугольника

Что такое периметр многоугольника

Периметр многоугольника в геометрии — это результат сложения длин всех его сторон.

Свойства многоугольника

Как вычислить периметр правильного многоугольника

Свойства правильного многоугольника

Формула

где a — длина стороны, n — количество сторон.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Для неправильного многоугольника

Описание

У неправильного многоугольника все стороны разного размера.

Формула

Его периметр (P) можно рассчитать, сложив все длины его сторон (a, b, c,d и т.д.). Это первый способ.

Второй способ: если есть стороны с одинаковыми длинами, формулу можно сократить, использовав умножение.

Дан прямоугольник со сторонами 4см, 4см, 2см и 2см. Чтобы узнать периметр, можно просто их все сложить, как показано в формуле выше. А можно сделать так: 4×2+2×2, так как стороны попарно равны.

Этот способ подойдет и для фигур с большим количеством сторон, некоторые из которых равны.

Дан восьмиугольник со сторонами 5см, 5см, 3см, 3см, 3см, 2см и 1см. Периметр можно высчитать сложением, а можно считать так: 5×2+3×3+2+1.

По заданным координатам

Как начертить многоугольник

Формула для расчета периметра

Далее нужно находить длины всех получившихся сторон.

В формулу нужно подставить вместо x и y координаты сторон.

Примеры решения задач

Задания приведены разного уровня сложности. Расположены по принципу «от простого к сложному».

Во всех задачах нужно найти периметр фигур. Этот вопрос дублироваться в каждом примере ниже не будет.

Пример 1

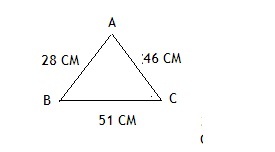
Дан треугольник ABC. AB=28см, BC=51см, AC=46см.

Пример 2

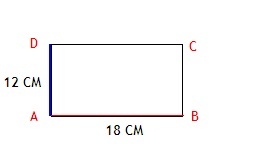
В прямоугольнике ABCD длина синей стороны 12 см, а красной 18 см.

Пример 3

Дан квадрат со стороной 12 см.

Мы знаем, что все стороны квадрата одинаковые. Их всего 4. Значит, P=12×4=48см.

Пример 4

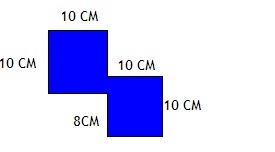
Дана фигура (данные на рисунке).

На рисунке мы видим восьмиугольник. У него шесть сторон по 10 см и две стороны по 8 см. Значит, P=10×6+8×2=60+16+76см.

Источник