Что такое периметр многоугольника 3 класс

Периметр

Периметр — это сумма длин всех сторон многоугольника.

Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.

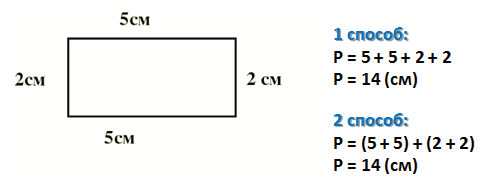
Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.

AB = 3 см, BC = 7 см

P_ABCD = (AB + BC) · 2
P_ABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

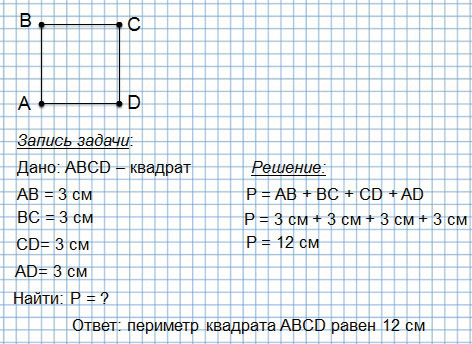
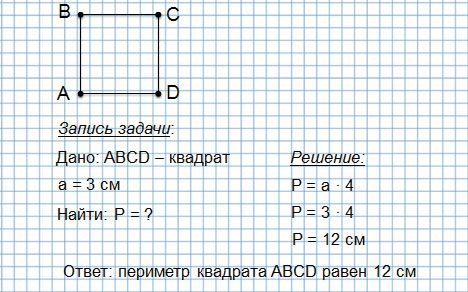
Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».

KE = 7 см

P_EKFM = 4 · KE
P_EKFM = 4 · 7 = 28 (см)

Как найти периметр многоугольника

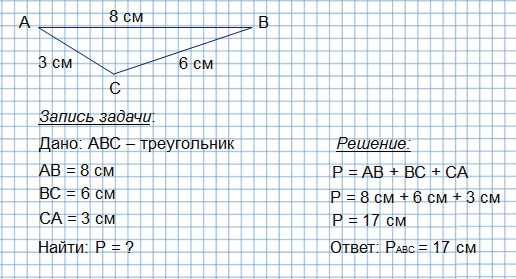
Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

P_ABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Источник

Периметр многоугольника

Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.

В математике периметр обозначают буквой P (пэ).

Периметр прямоугольника

Например, найдём периметр данного прямоугольника.

Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.

Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.

Формула для подсчета периметра прямоугольника:

(a + b) • 2

a – длина прямоугольника

b – ширина прямоугольника.

Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.

Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:

Периметр треугольника

Периметр квадрата

Первый способ (когда мы еще не знаем действие умножения):

Второй способ (когда мы изучили действие умножения):

Поделись с друзьями в социальных сетях:

Источник

Формула расчета периметра многоугольника

Что такое периметр многоугольника

Периметр многоугольника в геометрии — это результат сложения длин всех его сторон.

Свойства многоугольника

Как вычислить периметр правильного многоугольника

Свойства правильного многоугольника

Формула

где a — длина стороны, n — количество сторон.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Для неправильного многоугольника

Описание

У неправильного многоугольника все стороны разного размера.

Формула

Его периметр (P) можно рассчитать, сложив все длины его сторон (a, b, c,d и т.д.). Это первый способ.

Второй способ: если есть стороны с одинаковыми длинами, формулу можно сократить, использовав умножение.

Дан прямоугольник со сторонами 4см, 4см, 2см и 2см. Чтобы узнать периметр, можно просто их все сложить, как показано в формуле выше. А можно сделать так: 4×2+2×2, так как стороны попарно равны.

Этот способ подойдет и для фигур с большим количеством сторон, некоторые из которых равны.

Дан восьмиугольник со сторонами 5см, 5см, 3см, 3см, 3см, 2см и 1см. Периметр можно высчитать сложением, а можно считать так: 5×2+3×3+2+1.

По заданным координатам

Как начертить многоугольник

Формула для расчета периметра

Далее нужно находить длины всех получившихся сторон.

В формулу нужно подставить вместо x и y координаты сторон.

Примеры решения задач

Задания приведены разного уровня сложности. Расположены по принципу «от простого к сложному».

Во всех задачах нужно найти периметр фигур. Этот вопрос дублироваться в каждом примере ниже не будет.

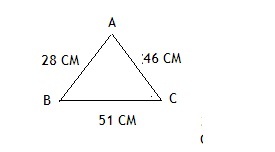
Пример 1

Дан треугольник ABC. AB=28см, BC=51см, AC=46см.

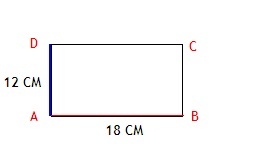
Пример 2

В прямоугольнике ABCD длина синей стороны 12 см, а красной 18 см.

Пример 3

Дан квадрат со стороной 12 см.

Мы знаем, что все стороны квадрата одинаковые. Их всего 4. Значит, P=12×4=48см.

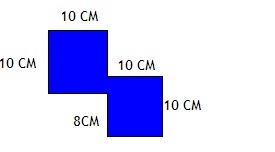
Пример 4

Дана фигура (данные на рисунке).

На рисунке мы видим восьмиугольник. У него шесть сторон по 10 см и две стороны по 8 см. Значит, P=10×6+8×2=60+16+76см.

Источник

Мультимедийный урок математики по теме «Периметр многоугольника»

Цель урока: познакомить детей с новым понятием «периметр многоугольника».

Задачи урока:

Материально-дидактическое оснащение урока: ноутбук;мультимедийный проектор; презентация Mickrosoft PowerPoint

Ход урока

I. Организационный момент.

— Создадим друг другу хорошее настроение.
— Улыбнулись друг другу.
— Пожелали получить «5».
— Крепко обняли себя и сказали: «У меня сегодня все получится!» (Презентация, слайд 1)

II. Сообщение темы и целей урока.

Внимание, девочки!
Внимание, мальчики!
Приготовьте ваши ручки,
Разомните пальчики.

Сегодня новые задачи будем решать.
Кто хочет получить отметку «пять»?
Тогда устный счёт пора начинать!

III. Устный счёт.

Счёт начинается по стрелке.

Ответы: 60, 100, 56, 94, 61, 42.

Счёт начинается по стрелке.

Ответы: 23, 39, 20, 30, 40, 5.

IV. Работа над новым материалом.

1. Актуализация опорных знаний.

а) Как называются эти геометрические фигуры? (Презентация, слайд 4)

1 – незамкнутая ломаная;

2 – замкнутая ломаная, многоугольник, четырёхугольник.

— Как найти длину ломаной? (Измерить звенья и сложить длины.)

б) Что изображено на следующем слайде? (Презентация, слайд 5)
(Многоугольники.)

— Назовите каждый многоугольник и покажите его границы.

(Учащиеся выходят к доске и указкой показывают границы каждого многоугольника. Ведут по сторонам многоугольника так, чтобы линия, которую опишет конец указки, представляла бы замкнутую ломаную.)

— Что представляет собой граница многоугольника? (Замкнутую ломаную.)

— Укажите возможные направления от дома.

— Какую фигуру представляет маршрут движения? (Замкнутую ломаную, треугольник.)

— Как найти длину маршрута? (Сложить по порядку длины всех отрезков пути.)

2. Создание проблемной ситуации. (Презентация, слайд 7)

— У вас на партах лежат фигуры (изготовлены из проволоки). Какую форму они имеют. (Форму треугольника.)

— Как по-другому можно назвать? (Замкнутая ломаная.)
— Из скольких звеньев состоит ломаная? (Из трёх.)
— Как найти её длину? (Измерить звенья и сложить все длины.)

— Выполните измерения. (4 см, 5 см, 3 см)
— Выполните вычисления. ( 4 см + 5 см + 3 см = 12 см)

— Как по-другому назвать звенья в этой фигуре? (Стороны.)
— Что измеряли и складывали? (Измеряли и складывали длины сторон треугольника.)

— Представьте, что вершины этого треугольника представляют места, куда вы хотите попасть.
— Как представить длину пройденного пути, если ученик побывал везде? (Предложения учащихся.)

— Запишем выражение.
4 см + 5 см + 3 см = 12 см – такова длина пути.

— Расправим стороны треугольника в одну линию и измерим при помощи линейки. Какова длина проволоки? (12 см)
— Сравним результат вычисления и измерения.
— Что мы с вами нашли этим выражением? (Длину пути, или сумму длин сторон треугольника.)

3. Знакомство с понятием «периметр многоугольника».

— Мы с вами нашли периметр треугольника.
— Так что же такое периметр треугольника? (Сумма длин сторон треугольника.)
— Не только треугольника, но и четырёхугольника, пятиугольника и т.д.

— Откройте учебник, страница 67. Решим задачу № 1.
На плане изображён дачный участок, размеры которого указаны на чертеже. Этот участок надо огородить забором.
* Какой длины должен быть забор?
* Сколькими способами можно решить задачу?
(Рассмотреть способ вычисления, предложенный авторами учебника. Предложить учащимся произвести сложение в другом порядке. Сравнить результаты вычислений. Сделать выводы.)

— Чтение и запоминание правила в учебнике страница 67. (Презентация, слайд 8)
— Математики – народ точный. Поэтому они решили периметр обозначать буквой Р.

4. Первичное закрепление. Игра «Не ошибись!» (Презентация, слайд 9)

— Я предлагаю вам упорядочить треугольники с помощью чисел, являющихся числовыми значениями их периметров. Заполните таблицу.

— Какое слово получили? (Периметр.)
— Так что такое периметр многоугольника? (Это сумма длин всех сторон многоугольника.)

5. Физкультминутка.

V. Закрепление изученного материала.

Работа в рабочей тетради № 1, страница 30, № 101. (Презентация, слайд 10)

а) Нахождение периметра четырёхугольника DKEF. (Фронтальная работа.)

— Измерьте и запишите длины каждой стороны четырёхугольника.

— Вспомните, как найти периметр четырёхугольника.
— Запишите выражение и вычислите его значение.
2 + 3 + 2 + 4 = 11 (см) – таков периметр четырёхугольника KDEF.
— Запишите ответ.

б) Нахождение периметра треугольника АВС. (Самостоятельная работа с последующей проверкой.) (Презентация, слайды 11, 12)

Вычислить периметр треугольника, если длина одной стороны 12 см, другой 15 см, а третья сторона меньше второй на 5 см.

VI. Подведение итогов урока.

Ответ: периметр.

— Что называется периметром многоугольника?
— Молодцы! Спасибо за урок! (Презентация, слайд 15)

VII. Домашнее задание.

Стр. 67 выучить правило, № 3 стр. 68.

Литература.

Источник

Как найти периметр фигуры

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Определение периметра

Периметр — это сумма длин всех сторон многоугольника.

Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.

Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.

Формулы нахождения периметра

Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.

Равносторонний многоугольник

У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.

P = 3 ⋅ a, где a — длина стороны.

Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.

А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.

Прямоугольник и параллелограмм

У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.

P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.

Окружность

У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.

L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!

Решение задач

Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?

Ответ: две другие стороны равны по 17 см.

Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.

Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!

Источник