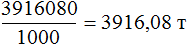Что такое периметр в геометрии
Периметр
Периметр — это сумма длин всех сторон многоугольника.
Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».
Периметр измеряется в единицах длины: мм, см, м, км и т.д.
При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.
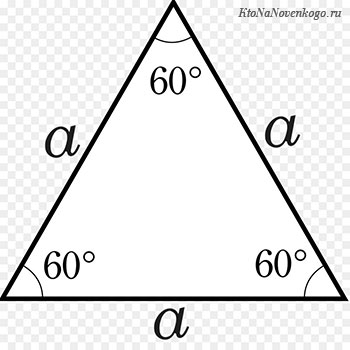
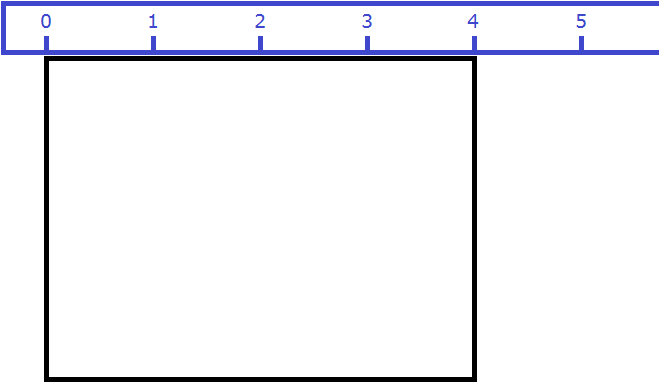
Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».
Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.

PABCD = (AB + BC) · 2
PABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)
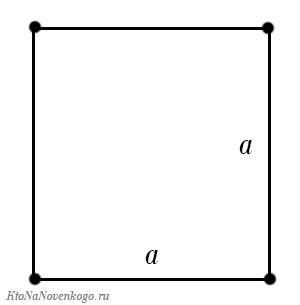
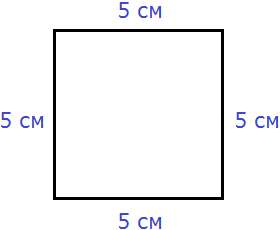
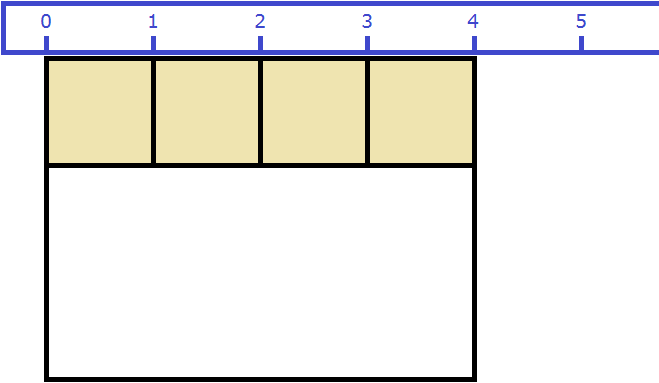
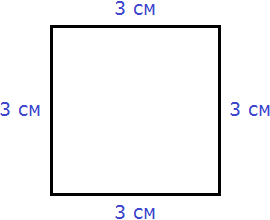
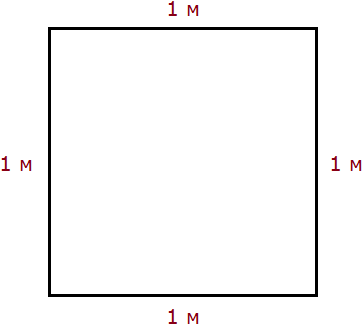
Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».

PEKFM = 4 · KE
PEKFM = 4 · 7 = 28 (см)
Как найти периметр многоугольника
Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

PABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)
Формулы периметра геометрических фигур
Формула периметра треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы периметра квадрата
Периметр квадрата равен произведению длины его стороны на четыре.
Периметр квадрата равен произведению длины его диагонали на два корня из двух.
Формула периметра прямоугольника
Периметр прямоугольника ABCD равен удвоенной сумме сторон, прилежащих к одному углу.
Формула периметра параллелограмма
Периметр параллелограмма ABCD равен удвоенной сумме сторон, прилежащих к одному углу
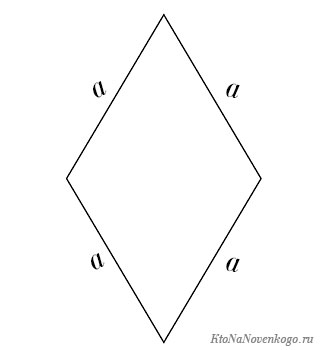
Формула периметра ромба
Периметр ромба равен произведению длины его стороны на четыре.
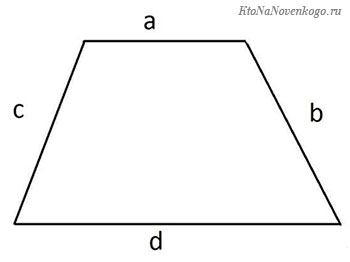
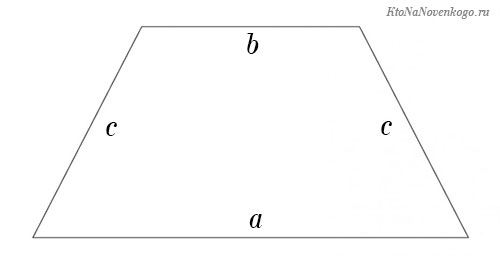
Формула периметра трапеции
Периметр трапеции равен сумме длин ее сторон.
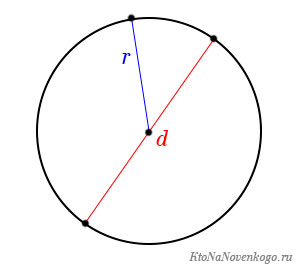
Формулы длины окружности.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Периметр – это границы измерений
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы подробно расскажем, что такое ПЕРИМЕТР, как он считается и каково его практическое применение.
Материал этот изучают в начальных классах школы, но далеко не всегда получается понятно объяснить простые вещи.
Что такое периметр
Периметр – это общая граница любой плоской геометрической фигуры. Измеряется в тех же величинах, что и стороны многоугольников.
У окружности тоже есть периметр. Хотя само слово в этом случае не применяют, говоря – длина окружности. Интересно, что само слово ПЕРИМЕТР изначально и обозначало окружность.
Так оно переводится с древнегреческого «περίμετρον». Но другой, более общий перевод – «измеряю вокруг», и тогда он подходит под все плоские геометрические фигуры как окружность, так и многоугольники.
Расчет периметра многоугольников
Считать периметр многоугольников очень просто. Надо всего лишь сложить длины всех сторон. И неважно, насколько замысловато выглядят сами фигуры.
Рассмотрим периметры самых популярных фигур.
Периметр треугольника
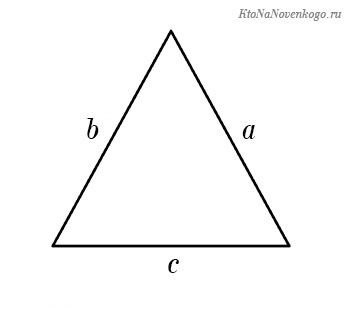
Как мы уже сказали, для расчета периметра треугольника надо просто сложить все его стороны.
Периметр обозначается латинской буквой «P». Он будет равен:
А если треугольник равносторонний или как его еще называют – правильный, то формула заметно упрощается.
Периметр прямоугольника
Отличительная черта прямоугольника – его противоположные стороны равны.
P = a + b + a + b = 2a + 2b = 2 (a + b)
Как и у треугольника, у прямоугольника есть частный случай, когда всего его стороны равны между собой. И всем известно, что называется такая фигура – квадрат.
Периметр параллелограмма
Если кто забыл, то параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны между собой.
И периметр у него считается точно так же, как и у прямоугольника. Более того, прямоугольник – это частный случай параллелограмма.
P = a + a + b + b = 2a + 2b = 2 (a + b)
У параллелограмма есть еще один частный случай. Фигура, у которой все стороны равны. И называется она – ромб.
Его периметр считается точно так же, как и у квадрата.
Периметр трапеции
И еще одна фигура, которая частенько встречается в жизни. И ее изучению посвящены отдельные главы школьной программы. Трапеция – это четырехугольник, у которого только две стороны лежат на параллельных прямых.
Но есть и частный случай, который называется равнобедренной трапецией. У этой фигуры непараллельные стороны равны между собой и идут под одинаковым наклоном.
P = a + b + c + c = a + b + 2c
Расчет длины окружности
Для расчета длины окружности, которая, по сути, и является периметром фигуры, есть своя формула. Вот только эту величину, в отличие от многоугольников, принято обозначать латинской буквой «L».
В этой формуле букой r обозначается радиус окружности, то есть расстояние от ее центра до границы. А буква π – это математическая постоянная, которая равна 3,14 (хотя на самом деле число знаков после запятой бесконечно).
Вместо заключения
Для чего в жизни нужно знать про ПЕРИМЕТР? Приведем самый простой пример.
Если вы на даче соберетесь поставить забор, вам нужно будет точно знать, сколько материала покупать. Для этого вы измерите свой участок по длине и ширине. Как правило, дачные участки имеют форму прямоугольников. Соответственно, после этого легко будет посчитать периметр:
где L – длина участка, а W – ширина. И уже с этими расчетами вы можете смело ехать в строительный магазин.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Не только это. Термин «периметр» весьма распространен в силовых структурах. Например: «Прапорщик Савельев отвечает за охрану периметра А, сержант Николаев — за периметр Б». То есть — какой-то ограниченный сектор с особым режимом, находящийся под сигнализацией и т.д.
Что такое периметр геометрической фигуры
В данной публикации мы рассмотрим, что такое периметр геометрической фигуры, как он считается, а также разберем примеры для демонстрации практического применения теоретических знаний.
Определение периметра
Периметр – это сумма длин всех сторон геометрической фигуры (треугольника, квадрата, трапеции, ромба и т.д.).
Для измерения периметра используются единицы длины: миллиметры (мм), сантиметры (см), метры (м), километры (км) и т.д.
Общепринятое обозначение периметра – это латинская буква “P“, под которой можно добавить сокращенное название фигуры или ее обозначение. Например:
Формулы периметра распространенных фигур
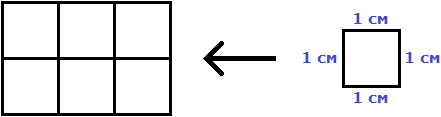
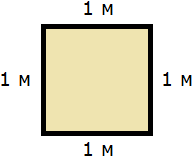
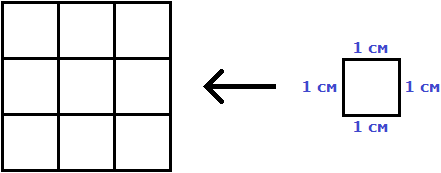
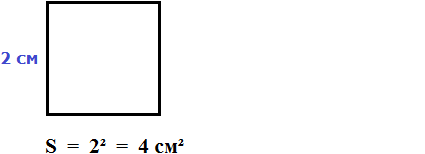
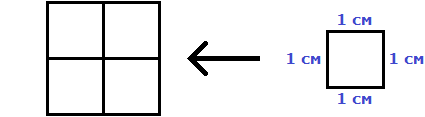
| Фигура | Название | Пояснение | ||||
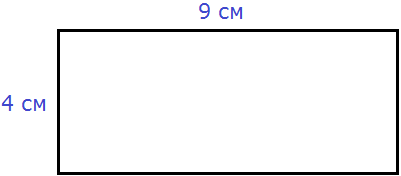
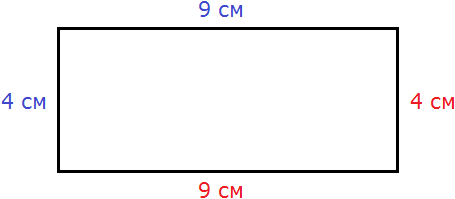
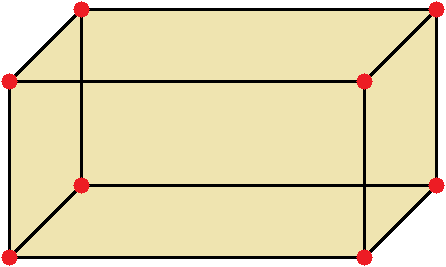
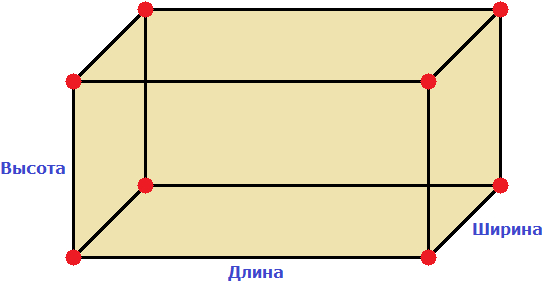
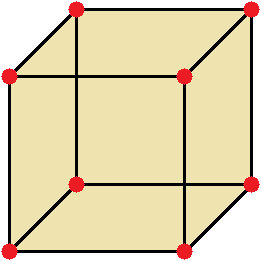
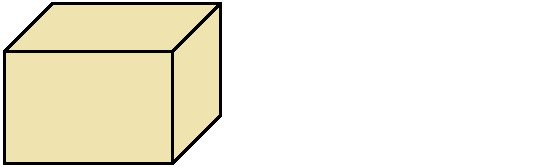
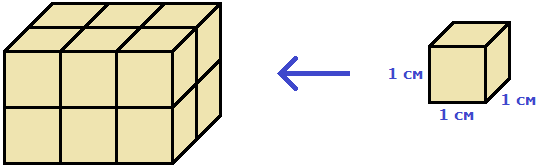
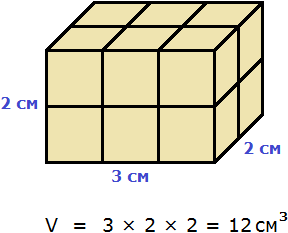
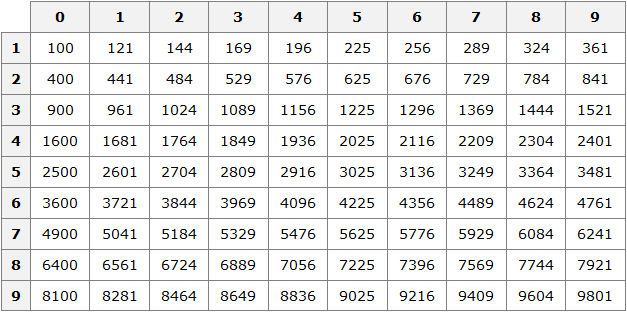
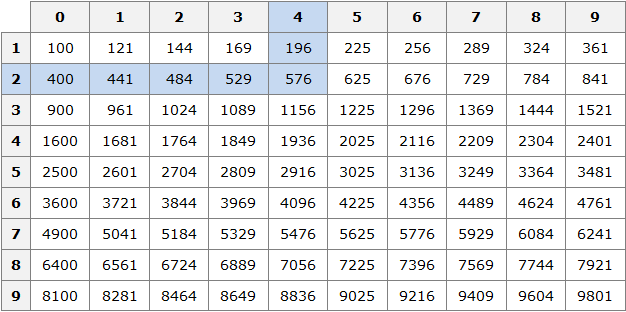
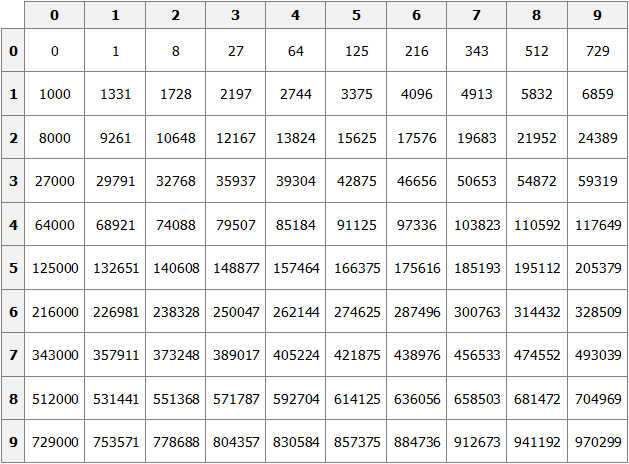
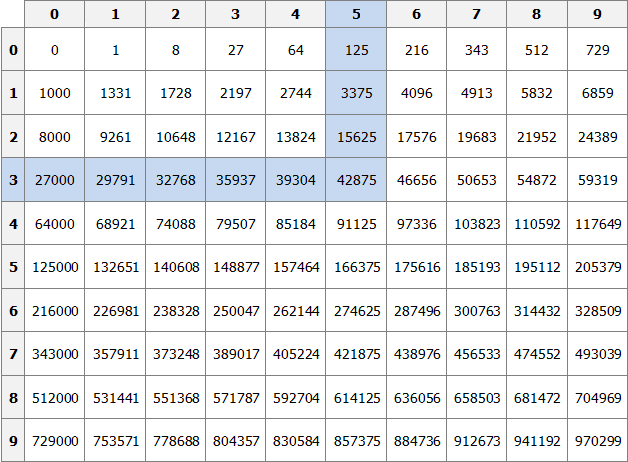
» data-order=» «> «>  | Квадрат | » data-order=» «> «>  | Прямоугольник | » data-order=» «> «>  | Треугольник |  Pквадр. = 5 + 5 + 5 + 5 = 4 ⋅ 5 = 20 см. Пример 2 Pпрямоуг. = 6 + 8 + 6 + 8 = (6 + 8) ⋅ 2 = 28 см. Пример 3 P = AB + BC + CD + DE + EH + HA = 5 + 3 + 5 + 4 + 6 + 5 = 28. Периметр, площадь и объёмПериметр геометрической фигурыПериметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений. Вычислим периметр следующей фигуры: Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см. У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно: Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters ). Тогда получим: P = 9 см + 4 см + 9 см + 4 см = 26 см. Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза» P = 2 × (9 + 4) = 18 + 8 = 26 см. Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см» Чтобы вычислить периметр, сложим все стороны: P = 5 см + 5 см + 5 см + 5 см = 20 см Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза Площадь геометрической фигурыПлощадь геометрической фигуры — это число, которое характеризует размер данной фигуры. Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола. Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр. Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре. Например, площадь следующего прямоугольника равна трём квадратным сантиметрам: Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру: Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза. Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам: Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру: Допустим, потребовалось измерить площадь следующей комнаты: Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах: Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату: Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров. Площадь прямоугольникаВ предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров. Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину. Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину. Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра: Теперь измерим ширину. Пусть она составила 3 метра: Умножим длину (4 м) на ширину (3 м). Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину: Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника: Площадь квадратаКвадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину. Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз: ОбозначенияПлощадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу Например, вычислим площадь квадрат со стороной 2 см. Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам: Вычислим площадь квадрата со стороной 3 метра Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам: Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам: Перевод единиц измерения площадиЕдиницы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров: Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах. 1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру. Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100 S = 100 2 = 10 000 см 2 Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров. 1 м 2 = 10 000 см 2 Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах. Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000. Например, переведём 100 000 см 2 в квадратные метры. Рассуждать в этом случае можно так: « если 10 000 см 2 это один квадратный метр, то сколько раз 100 000 см 2 будут содержать по 10 000 см 2 » 100 000 см 2 : 10 000 см 2 = 10 м 2 Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км 2 в квадратные метры. S = 1000 2 = 1 000 000 м 2 Получается, что на один квадратный километр приходится один миллион квадратных метров: 1 км 2 = 1 000 000 м 2 Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах. Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000. Итак, вернёмся к нашей задаче. Требовалось перевести 2 км 2 в квадратные метры. Умножим 2 км 2 на 1 000 000 2 км 2 × 1 000 000 = 2 000 000 м 2 Например, переведём 3 500 000 м 2 в квадратные километры. Рассуждать в этом случае можно так: « если 1 000 000 м 2 это один квадратный километр, то сколько раз 3 500 000 м 2 будут содержать по 1 000 000 м 2 » 3 500 000 м 2 : 1 000 000 м 2 = 3,5 км 2 Пример 2. Выразить 7 м 2 в квадратных сантиметрах. Умножим 7 м 2 на 10 000 7 м 2 = 7 м 2 × 10 000 = 70 000 см 2 Пример 3. Выразить 5 м 2 13 см 2 в квадратных сантиметрах. 5 м 2 13 см 2 = 5 м 2 × 10 000 + 13 см 2 = 50 013 см 2 Пример 4. Выразить 550 000 см 2 в квадратных метрах. 550 000 см 2 : 10 000 см 2 = 55 м 2 Пример 5. Выразить 7 км 2 в квадратных метрах. Умножим 7 км 2 на 1 000 000 7 км 2 × 1 000 000 = 7 000 000 м 2 Пример 6. Выразить 8 500 000 м 2 в квадратных километрах. 8 500 000 м 2 × 1 000 000 м 2 = 8,5 км 2 Единицы измерения площади земельных участковПлощади небольших земельных участков удобно измерять в квадратных метрах. Площади более крупных земельных участков измеряются в арах и гектарах. Ар (сокращённо: a) — это площадь равная ста квадратным метрам ( 100 м 2 ). В виду частого распространения такой площади ( 100 м 2 ) она стала использоваться, как отдельная единица измерения. Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м 2 каждый, то есть: 3 а = 100 м 2 × 3 = 300 м 2 10 соток = 1000 м 2 20 га = 10 000 м 2 × 20 = 200 000 м 2 Прямоугольный параллелепипед и кубПрямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин. На рисунке показан прямоугольный параллелепипед: Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины. Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота: Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб: Объём геометрической фигурыОбъём геометрической фигуры — это число, которое характеризует вместимость данной фигуры. Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр. Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру. Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам: Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см: Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см 3 ). Тогда объём V рассмотренного нами параллелепипеда равен 12 см 3 V = 12 см 3 Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты. V = abc где, a — длина, b — ширина, c — высота Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту. Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба: Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам: Действительно, в исходный куб вмещается 27 кубиков длиной 1 см Таким образом, объём куба вычисляется по следующему правилу: Кубический дециметр. Кубический метрНе все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах ( м 3 ). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах ( дм 3 ). Другое название одного кубического дециметра – один литр. 1 дм 3 = 1 литр Перевод единиц измерения объёмаЕдиницы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров: Пример 1. Выразить 1 кубический метр в кубических сантиметрах. Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру. Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб: V = 100 3 = 1 000 000 см 3 Получается, что на один кубический метр приходится один миллион кубических сантиметров: 1 м 3 = 1 000 000 см 3 Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах. Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000. Например, переведём 300 000 000 см 3 в кубические метры. Рассуждать в этом случае можно так: « если 1 000 000 см 3 это один кубический метр, то сколько раз 300 000 000 см 3 будут содержать по 1 000 000 см 3 » 300 000 000 см 3 : 1 000 000 см 3 = 300 м 3 Пример 2. Выразить 3 м 3 в кубических сантиметрах. Умножим 3 м 3 на 1 000 000 3 м 3 × 1 000 000 = 3 000 000 см 3 Пример 3. Выразить 60 000 000 см 3 в кубических метрах. 60 000 000 см 3 : 1 000 000 см 3 = 60 м 3 Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру. 1 литр = 1 дм 3 Пример 1. Перевести 5 литров в кубические дециметры. Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1 Пример 2. Перевести 6000 литров в кубические метры. Шесть тысяч литров это шесть тысяч кубических дециметров: 6000 л × 1 = 6000 дм 3 Теперь переведём эти 6000 дм 3 в кубические метры. Длина, ширина и высота одного кубического метра равны 10 дм Если вычислить объём этого куба в дециметрах, то получим 1 000 дм 3 V = 10 3 = 1000 дм 3 Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм 3 содержит по 1 000 дм 3 6 000 дм 3 : 1 000 дм 3 = 6 м 3 Таблица квадратовВ жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень. Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов. Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа. Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц. Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576 24 2 = 576 Таблица кубовКак и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов. Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875. 35 3 = 42875 Задания для самостоятельного решенияРешение a = 6, b = 2 Ответ: периметр прямоугольника равен 16 см. Решение Решение Ответ: ширина прямоугольника составляет 2 см. Решение S = a 2 Решение Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см 3 Решение Ответ: высота прямоугольного параллелепипеда равна 4 см. Решение Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном. Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза. Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза Ответ: пшеницей засеяно 12 га. Решение a = 42 м Определим объем зернохранилища: V = abc = 42 × 30 × 4,2 = 5292 м 3 Определите сколько тонн зерна вмещает зернохранилище: 5292 × 740 = 3916080 кг Переведём килограммы в тонны: Ответ: зернохранилище вмещает 3916,08 тонн зерна. Решение Определим сколько литров в минуту вливается через вторую трубу: 25 л/мин × 0,75 = 18,75 л/мин Определим сколько литров в минуту вливается в бассейн через обе трубы: 25 л/мин + 18,75 л/мин = 43,75 л/мин Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин 43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л 1 л = 1 дм 3 35 525 л = 35 525 дм 3 Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна: 35 525 дм 3 : 1000 дм 3 = 35,525 м 3 Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим: Ответ: высота (глубина) бассейна составляет 1,75 м. Понравился урок? Возникло желание поддержать проект? 9 thoughts on “Периметр, площадь и объём”Ура. Вы снова в деле. Всегда будем рады новым урокам. Благодарю. Все четко, последовательно, без воды. Пожалуйста не останавливайтесь! Желаю успехов в ваших проектах. Продовжуйте працювати! Спасибі, що ви випукаєте нові уроки. Чекаю на нові уроки із захопленням. Продовжуйте працювати! Спасибі, що ви випукаєте нові уроки, я чекаю на них із захопленням.
|

















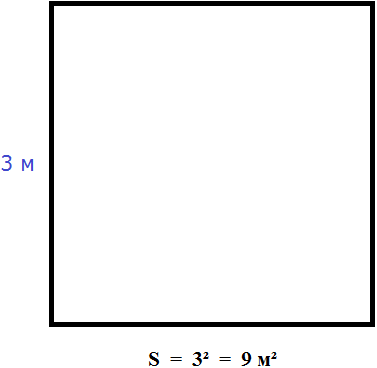
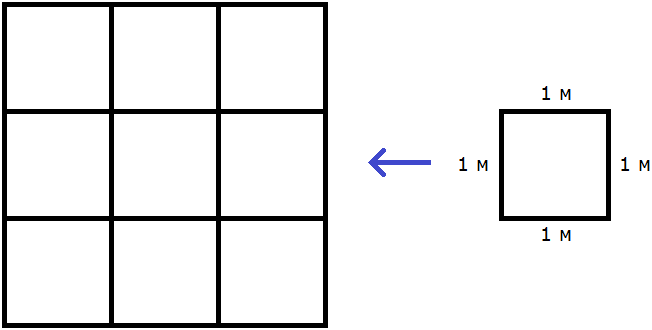
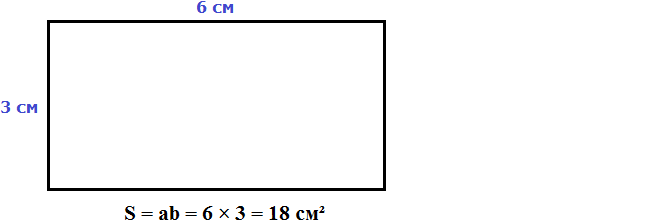
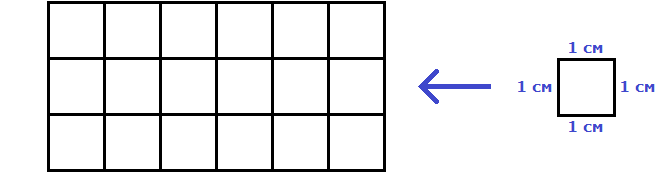
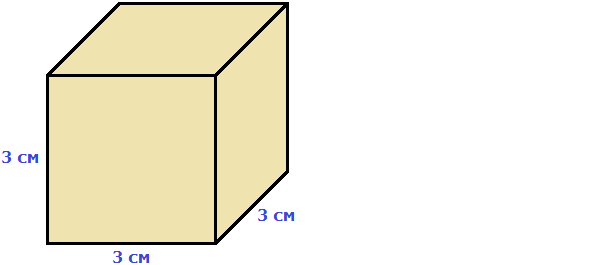
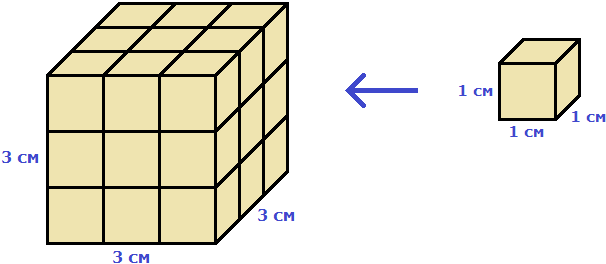
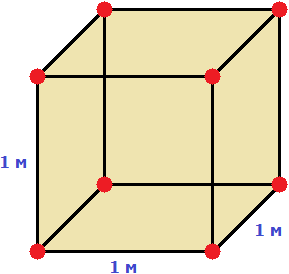
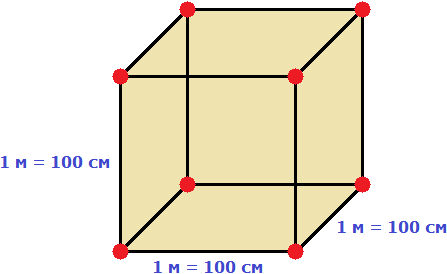
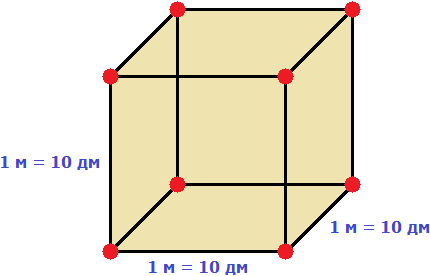
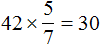 м
м