Что такое период единица измерения

Период колебаний

Из Википедии — свободной энциклопедии

В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическим колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Единицы измерения: секунда и, в принципе, вообще единицы измерения времени.

Период колебаний связан соотношением взаимной обратности с частотой:

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота [3] колебаний его волновой функции).

Теоретическое вычисление периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решётки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Источник

Период и частота колебаний

Период колебаний

Периодом ($T$) колебаний называют время, за которое совершается одно полное колебание.

Разные периодические процессы, (процессы, повторяющиеся через равные промежутки времени) можно представить в виде совокупности наложенных гармонических колебаний.

Формулы для вычисления периода простейших колебательных систем

Период колебаний пружинного маятника определим как:

Период колебаний математического маятника зависит от ускорения свободного падения ($g$) и длины подвеса ($l$)

Формула для вычисления периода колебаний физического маятника представляет собой выражение:

Единицами измерения периода служат единицы времени, например секунды.

Частота колебаний

Частота колебаний связана с циклической частотой как:

Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:

Примеры задач с решением

Решение. Из уравнения колебаний:

заключаем, что это гармонические колебания, так как они происходят по закону синуса следовательно, они являются периодическими. Период найдем, зная циклическую частоту колебаний:

Подставляя имеющиеся данные, вычислим период колебаний:

Частоту колебаний найдем как величину, обратную периоду:

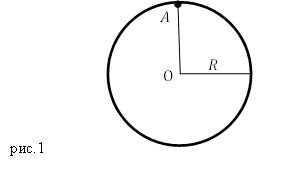
Задание. Какими будут период и частота малых колебаний тонкого обруча, который висит на гвозде (точка А), вбитом горизонтально в стену (рис.1)? Колебания совершаются в плоскости параллельной стене. Радиус обруча R.

Решение. В этой задаче мы имеем дело с физическим маятником период которого, найдем, используя формулу:

Осью вращения обруча является гвоздь, находящийся в точке А. Цент масс обруча находится в его геометрическом центре, точке О, следовательно, расстояние от центра масс до оси вращения обруча (рис.1) равно:

Используя формулы (2.1) (2.2) и (2.4), имеем:

Отталкиваясь от полученного результата, найдем частоту колебаний как:

Источник

Характеристики колебаний

Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):

Такие величины, как амплитуду и период, можно определить по графику колебаний.

Начальную фазу, так же, определяют по графику, с помощью интервала времени \(\large \Delta t\), на который относительно нуля сдвигается начало ближайшего периода.

Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.

А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.

Что такое амплитуда

Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.

Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.

В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.

Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.

К примеру, пусть колеблется величина \( \large x \). Тогда символом \( \large x_ <0>\) обозначают амплитуду колебаний этой величины.

Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».

С помощью графика амплитуду можно определить так (рис. 2):

Что такое период

Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.

Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.

\( \large T \left( c \right) \) – период колебаний.

Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.

Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.

Период – это время одного полного колебания.

На графике период найти удобнее одним из таких способов (рис. 4):

Что такое частота

Обозначают ее с помощью греческой буквы «ню» \( \large \nu \).

Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».

Поэтому, размерность частоты — это единицы колебаний в секунду:

\( \large \nu \left( \frac<1> \right) \).

Иногда в учебниках встречается такая запись \( \large \displaystyle \nu \left( c^ <-1>\right) \), потому, что по свойствам степени \( \large \displaystyle \frac<1> = c^ <-1>\).

Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.

Одно колебание в секунду соответствует частоте в 1 Герц.

Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:

Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).

Что такое циклическая частота

Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол \(\large 2\pi\) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный \(\large 2\pi\) секунд.

Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:

\( \large \displaystyle \omega \left( \frac<\text<рад>> \right) \)

Примечание: Величину \( \large \omega \) так же называют круговой частотой, а еще — угловой скоростью (ссылка).

Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за \(\large 2\pi\) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный \(\large 2\pi\) секунд?».

Обычная \( \large \nu \) и циклическая \( \large \omega \) частота колебаний связаны формулой:

Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.

Чтобы с помощью графика колебаний определить величину \( \large \omega \), нужно сначала найти период T.

Затем, воспользоваться формулой \( \large \displaystyle \nu = \frac<1>\) и вычислить частоту \( \large \nu \).

И только после этого, с помощью формулы \( \large \omega = 2\pi \cdot \nu \) посчитать циклическую \( \large \omega \) частоту.

Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.

Определить величину \( \large \omega \) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный \(\large 2\pi\), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).

Что такое начальная фаза и как определить ее по графику колебаний

Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.

Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_ <0>\).

\(\large \varphi_ <0>\left(\text <рад>\right) \) — начальная фаза, измеряется в радианах (или градусах).

Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.

Рассмотрим теперь, как величина \(\large \varphi_ <0>\) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.

Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_ <0>\) принимаем равной нулю.

Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_ <0>\) будет отличаться от нулевого значения.

Определим угол \(\large \varphi_ <0>\) с помощью графика колебаний.

Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_ <0>\) — в радианах. Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_ <0>\).

Как вычислить начальный угол по интервалу смещения

Алгоритм нахождения начального угла состоит из нескольких несложных шагов.

\[\large T = 5 – 1 = 4 \left( \text <сек>\right)\]

Из графика следует, что период T = 4 сек.

Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.

Для этого используем формулу:

\(\large \displaystyle \frac<1> <4>\cdot 2\pi = \frac<\pi > <2>=\varphi_ <0>\)

Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac<\pi > <2>\) – это начальная фаза для красной кривой на рисунке.

Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:

Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac<\pi > <2>\) имеет знак «плюс».

Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая \(\large \varphi_ <0>= 0 \).

Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».

А если функция сдвинута вправо и запаздывает относительно обычной функции, величину \(\large \varphi_ <0>\) записываем со знаком «-».

Примечания:

Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.

Что такое фаза колебаний

Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.

В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают \(\varphi\).

Различия между фазой и начальной фазой

Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.

Первый угол называют начальной \( \varphi_<0>\) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто \( \varphi\) фазой (рис. 10б) – это величина переменная.

Как на графике колебаний отметить фазу

На графике колебаний фаза \(\large \varphi\) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.

На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.

А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.

Как определить фазу с помощью формулы

Пусть нам известны величины \(\large \omega\) — циклическая частота и \(\large \varphi_<0>\) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.

Время колебаний t будет величиной переменной.

Фазу \(\large \varphi\), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:

Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

\( \large \varphi_<01>\) – для первого процесса и,

\( \large \varphi_<02>\) – для второго процесса.

Определим разность фаз между первым и вторым колебательными процессами:

Величина \(\large \Delta \varphi \) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

\( \large T \left( c \right) \) – время одного полного колебания (период колебаний);

\( \large N \left( \text <шт>\right) \) – количество полных колебаний;

\( \large t \left( c \right) \) – общее время для нескольких колебаний;

\(\large \nu \left( \text <Гц>\right) \) – частота колебаний.

\(\large \displaystyle \omega \left( \frac<\text<рад>> \right) \) – циклическая (круговая) частота колебаний.

\(\large \varphi_ <0>\left( \text <рад>\right) \) — начальная фаза;

\(\large \varphi \left( \text <рад>\right) \) – фаза (угол) в выбранный момент времени t;

\(\large \Delta t \left( c \right) \) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.

Источник

Период, частота, амплитуда и фаза переменного тока

Период и частота переменного тока

Время, в течение которого совершается одно полное изме­нение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания пере­менного тока (рисунок 1).

Период выражают в секундах и обозначают буквой Т.

Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.

Число полных изменений ЭДС или число оборотов ради­уса-вектора, то есть иначе говоря, число полных циклов колеба­ний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.

Частота обо­значается буквой f и выражается в периодах в секунду или в герцах.

Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.

1000 Гц = 10 3 Гц = 1 кГц;

1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Чем быстрее происходит изменение ЭДС, то есть чем бы­стрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.

Математическая связь между периодом и частотой переменного тока и напряжения выра­жается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

Т = 1/f = 1/50 = 0,02 сек.

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:

f = 1/T=1/0,02 = 100/2 = 50 Гц

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Частоты от 20 до 20 000 Гц называются звуковыми часто­тами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие вы­сокие частоты называются радиочастотами или колебаниями высокой частоты.

Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.

Амплитуда переменного тока

Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно бук­вами Im, Em и Um (рисунок 1).

Угловая (циклическая) частота переменного тока.

Скорость вращения радиуса-вектора, т. е. изменение ве­личины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (оме­га). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.

Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.

Рисунок 2. Радиан.

1рад = 360°/2

? = 6,28*f = 2f

Фаза переменного тока.

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза пока­зывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.

Полный оборот радиуса-вектора равен 360°. С началом но­вого оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следова­тельно, все фазы ЭДС будут повторяться в прежнем поряд­ке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обо­их этих случаях радиус-вектор занимает одинаковое положе­ние, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник

Какая формула периода?

Кроме того, почему V WR?

Аналогично, в какой единице измеряется период?

Период относится ко времени, когда что-то должно произойти, и измеряется в секунд / цикл. В этом случае на 11 колебательных цикла приходится 33 секунд.

Здесь, что такое периодические волны?

Период волны: Время, необходимое для прохождения двух последовательных гребней (одной длины волны) заданной точки.. Период волны часто указывается в секундах, например, одна волна каждые 6 секунд.

Угловая скорость ω аналогична линейной скорости v. Связь между линейной скоростью и угловой скоростью можно записать двумя разными способами: v = rω или ω = v / r.

Есть ли у Омеги угловая скорость?

В физике угловая скорость относится к тому, насколько быстро объект вращается или вращается относительно другой точки, то есть насколько быстро угловое положение или ориентация объекта изменяется со временем. … Угловая скорость обычно обозначается символом омега (ω, иногда Ω).

Что называется периодом времени?

Что такое период 2 Гц?

Какой пример периода?

Примером периода является первое занятие дня. Пример периода: женский менструальный цикл. Знак препинания (.), Обозначающий точку, ставится в конце повествовательных предложений и других утверждений, которые считаются завершенными, а также после множества сокращений.

Какой период хорошей волны?

Что означает более высокий период волны?

Какой период волн подходит для катания на лодке?

Для судоводителей длинные периоды волн (например, 12 секунд) лучше подходят для плавания, потому что это обычно означает, что большая часть волн будет волной, что означает более плавную поездку для небольших лодок.

Какая связь между периодом и частотой?

Как писать Гц?

Герц (символ: Гц) является производной единицей частоты в Международной системе единиц (СИ) и определяется как один цикл в секунду.

Что такое единица измерения вязкости в системе СИ?

Что такое R * Omega?

Чему равна угловая скорость?

При равномерном круговом движении угловая скорость () является векторной величиной и равна угловое смещение (Δ, векторная величина), деленное на изменение во времени (Δ).

Что такое Омега?

Что такое R Omega?

В каком направлении угловая скорость?

Направление угловой скорости по оси вращения, и указывает от вас, если объект вращается по часовой стрелке, и к вам, если объект вращается против часовой стрелки. В математике это описывается правилом правой руки.

Что такое сленг для периода?

Тетя Фло/ Тетя Флоу. Время месяца. На тряпке. Красный прилив / армия.

Время частота продольных энергетических волн.

Однако время непостоянно. Он меняется с движением. Доказательства связи времени с частотой волн основаны на теории относительности Эйнштейна.

Как называется связь между частотой и периодом?

Источник