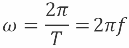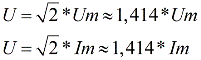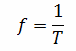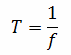Основные параметры переменного тока: период, частота, фаза, амплитуда, гармонические колебания

Переменный ток — электрический ток, направление и сила которого изменяются периодически. Так как обычно сила переменного тока изменяется по синусоидальному закону, то переменный ток представляет собой синусоидальные колебания напряжения и силы тока.

Поэтому к переменному току применимо все то, что относится к синусоидальным электрическим колебаниям. Синусоидальные колебания — колебания, при которых колеблющаяся величина изменяется по закону синуса. В данной статье поговорим о параметрах переменного тока.

Изменение ЭДС и изменение тока линейной нагрузки, подключенной к такому источнику, будет происходить по синусоидальному закону. При этом переменные ЭДС, переменные напряжения и токи, можно характеризовать основными четырьмя их параметрами:

Есть и вспомогательные параметры:

Далее рассмотрим все эти параметры по отдельности и во взаимосвязи.

Период — время, в течение которого система, совершающая колебания, проходит через все промежуточные состояния и нале снова возвращается к исходному.

Периодом Т переменного тока называется промежуток времени, за который ток или напряжение совершает один полный цикл изменений.

Поскольку источником переменного тока является генератор, то период связан со скоростью вращения его ротора, и чем выше скорость вращения витка или ротора генератора, тем меньшим оказывается период генерируемой переменной ЭДС, и, соответственно, переменного тока нагрузки.

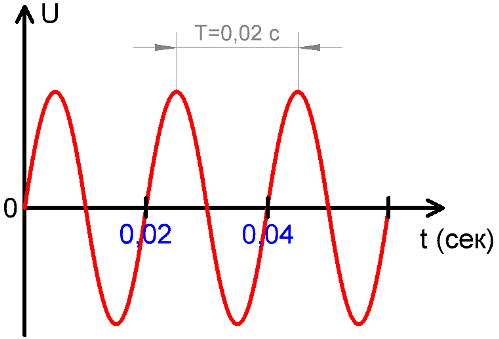
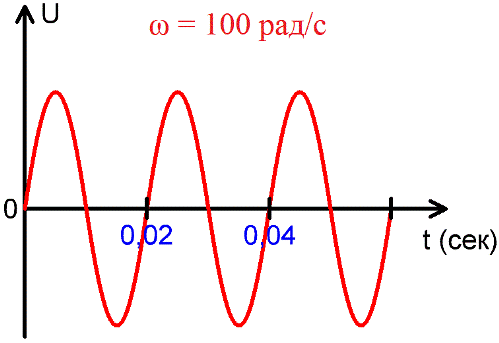
Период измеряется в секундах, миллисекундах, микросекундах, наносекундах, в зависимости от конкретной ситуации, в которой данный ток рассматривается. На вышеприведенном рисунке видно, как напряжение U с течением времени изменяется, имея при этом постоянный характерный период Т.

Частота f является величиной обратной периоду, и численно равна количеству периодов изменения тока или ЭДС за 1 секунду. То есть f = 1/Т. Единица измерения частоты — герц (Гц), названная в честь немецкого физика Генриха Герца, внесшего в 19 веке немалый вклад в развитие электродинамики. Чем меньше период, тем выше частота изменения ЭДС или тока.

Сегодня в России стандартной частотой переменного тока в электрических сетях является 50 Гц, то есть за 1 секунду происходит 50 колебаний сетевого напряжения.

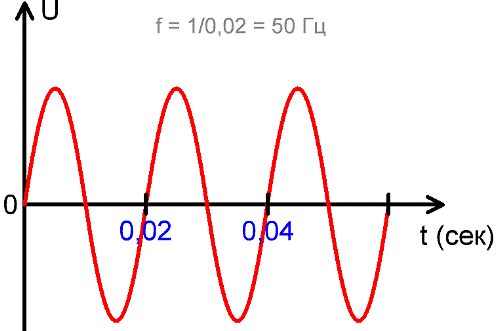
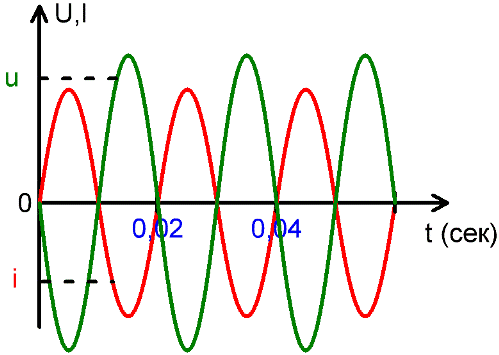
В других областях электродинамики используются и более высокие частоты, например 20 кГц и более — в современных инверторах, и до единиц МГц в более узких сферах электродинамики. На приведенном выше рисунке видно, что за одну секунду происходит 50 полных колебаний, каждое из которых длится 0,02 секунды, и 1/0,02 = 50.

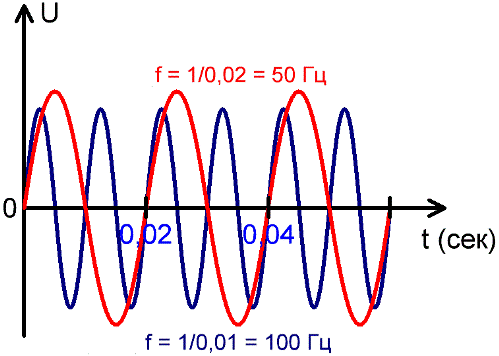
По графикам изменения синусоидального переменного тока с течением времени видно, что токи различной частоты содержат разное количество периодов на одном и том же отрезке времени.

Угловая частота — число колебаний, совершаемых за 2пи сек.

За один период фаза синусоидальной ЭДС или синусоидального тока изменяется на 2пи радиан или на 360°, поэтому угловая частота переменного синусоидального тока равна:

Пользоваться числом колебаний на 2пи сек. (а не за 1 сек.) удобно потому, что в формулах, выражающих закон изменения напряжений и токов при гармонических колебаниях, выражающих индуктивное или емкостное сопротивление переменному току, и во многих других случаях частота колебаний n фигурируют вместе с множителем 2пи.

Фаза — состояние, стадия периодическою процесса. Более определенный смысл имеет понятие фаза в случае синусоидальных колебаний. На практике обычно играет роль не фаза сама по себе, а сдвиг фаз между какими-либо двумя периодическими процессами.

В данном случае под термином «фаза» понимают стадию развития процесса, и в данном случае, применительно к переменным токам и напряжениям синусоидальной формы, фазой называют состояние переменного тока в определенный момент времени.

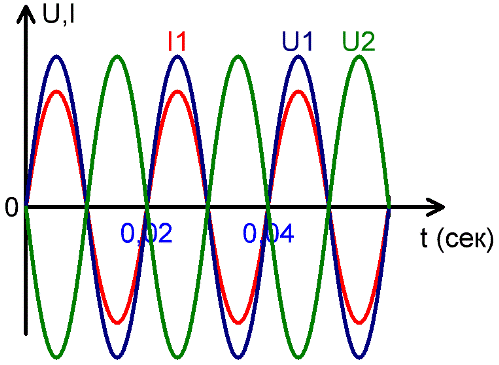
На рисунках можно видеть: совпадение напряжения U1 и тока I1 по фазе, напряжения U1 и U2 в противофазе, а также сдвиг по фазе между током I1 и напряжением U2. Сдвиг по фазе измеряется в радианах, долях периода, в градусах.

Говоря о величине синусоидального переменного тока или синусоидальной переменной ЭДС, наибольшее значение ЭДС или тока называют амплитудой или амплитудным (максимальным) значением.

Амплитуда — наибольшее значение величины, совершающей гармонические колебания (например, максимальное значение силы тока в переменном токе, отклонение колеблющегося маятника от положения равновесия), наибольшее отклонение колеблющейся величины от некоторого значения, условно принятого за начальное нулевое.

Строго говоря, термин амплитуда относится только к синусоидальным колебаниям, но его обычно (не вполне правильно) применяют в указанном выше смысле ко всяким колебаниям.

Гармонические колебания — колебания, в которых колеблющаяся величина, например напряжение в электрической цепи, меняется во времени по гармоническому синусоидальному или косинусоидальному закону. Графически представляются кривой — синусоидой.

Реальные процессы могут лишь приближенно быть гармоническими колебаниями. Однако если колебания отражают наиболее характерные черты процесса, то такой процесс считают гармоническими, что существенно облегчает решение многих физических и технических задач.

Движения, близкие к гармоническим колебаниям, совершаются в различных системах: механических (колебания маятника), акустических (колебания столба воздуха в органной трубе), электромагнитных (колебания в LC-контуре) и др. Теория колебаний рассматривает эти различные по физической природе явления с единой точки зрения и определяет их общие свойства.

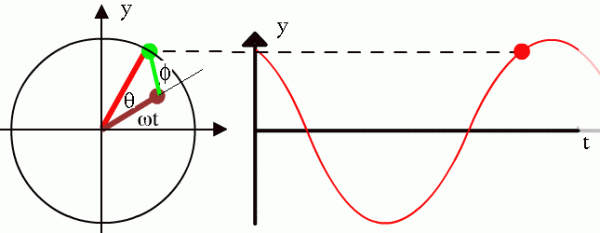
Графически гармонические колебания удобно представить с помощью вектора, вращающегося с постоянной угловой скоростью вокруг оси, перпендикулярной к этому вектору и проходящей через его начало. Угловая скорость вращения вектора соответствует круговой частоте гармонического колебания.

Векторная диаграмма одного гармонического колебания

Периодический процесс любой формы может быть разложен в бесконечный ряд простых гармонических колебаний с различными частотами, амплитудами и фазами.

Гармоника — гармоническое колебание, частота которого в целое число раз больше частоты некоторого другого колебания, называемого основным тоном. Номер гармоники указывает, во сколько именно раз частота ее больше частоты основного тона (например, третья гармоника — гармоническое колебание с частотой, втрое большей, чем частота основного тона).

Всякое периодическое, но не гармоническое (т. е. отличающееся по форме от синусоидального) колебание может быть представлено в виде суммы гармонических колебаний — основного тона и ряда гармоник. Чем больше рассматриваемое колебание отличается по форме от синусоидального, тем большее число гармоник оно содержит.

Мгновенное значение u и i

Значение ЭДС или тока в конкретный текущий момент времени называется мгновенным значением, они обозначаются маленькими буквами u и i. Но поскольку эти значения все время меняются, то судить о переменных токах и ЭДС по ним неудобно.

Действующие значения I, E и U

Способность переменного тока к совершению какой-нибудь полезной работы, например механически вращать ротор двигателя или производить тепло на нагревательном приборе, удобно оценивать по действующим значениям ЭДС и токов.

Так, действующим значением тока называется значение такого постоянного тока, который при прохождении по проводнику в течение одного периода рассматриваемого переменного тока, производит такую же механическую работу или такое же количество теплоты, что и данный переменный ток.

Действующие значения напряжений, ЭДС и токов обозначают заглавными буквами I, E и U. Для синусоидального переменного тока и для синусоидального переменного напряжения действующие значения равны:

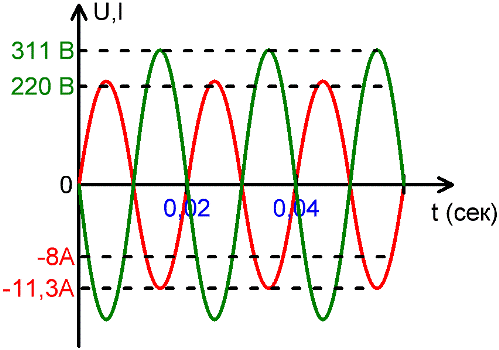
Действующее значение тока и напряжения удобно практически использовать для описания электрических сетей. Например значение в 220-240 вольт — это действующее значение напряжения в современных бытовых розетках, а амплитуда гораздо выше — от 311 до 339 вольт.

Так же и с током, например когда говорят, что по бытовому нагревательному прибору протекает ток в 8 ампер, это значит действующее значение, в то время как амплитуда составляет 11,3 ампер.

Так или иначе, механическая работа и электрическая энергия в электроустановках пропорциональны действующим значениям напряжений и токов. Значительная часть измерительных приборов показывает именно действующие значения напряжений и токов.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Период и частота переменного тока

Под этим термином «переменный электрический ток» следовало бы понимать ток, изменяющийся во времени любым образом, соответственно введенному в математику понятию «переменная величина».

Однако в электротехнику термин «переменный электрический ток» вошел в значении электрического тока, вменяющегося по направлению (в противовес электрическому току постоянного направления), а следовательно, и по величине, так как физически нельзя представлять себе изменения электрического тока по направлению без соответствующих изменений по величине.

Движение электронов в проводе сначала в одну сторону, а затем в другую называют одним колебанием переменного тока. За первым колебанием следует второе, затем третье и т. д. При колебаниях тока в проводе вокруг него происходит соответствующее колебание магнитного поля.

Время одного колебания называют периодом и обозначают буквой Т. Период выражают в секундах или в единицах, составляющих доли секунды.

Важной величиной, характеризующей переменный ток, является частота. Она представляет собой число колебаний или число периодов в секунду и обозначается буквой f или F.

Единицей частоты служит герц, названный в честь немецкого ученого Г. Герца и обозначаемый сокращенно буквами Гц (или Hz). Если в одну секунду происходит одно полное колебание, то частота равна одному герцу.

Когда в течение секунды совершается десять колебаний, то частота составляет 10 Гц. Частота и период являются обратными величинами:

При частоте 10 Гц период равен 0,1 с. А если период равен 0,01 с, то частота составляет 100 Гц.

Частота — важнейшая характеристика переменного тока. Электрические машины и аппараты переменного тока могут нормально работать только на той частоте, на которую они рассчитаны.

Параллельная работа электрических генераторов и станций на общую сеть возможна только на одной и той же частоте. Поэтому во всех странах частота переменного тока, производимого электростанциями, стандартизуется законом.

В электрической сети переменного тока частота равна 50 Гц. Ток пятьдесят раз в секунду идет в одну сторону и пятьдесят раз в обратную. Сто раз в секунду он достигает амплитудного значения и сто раз становится равным нулю, т. е. сто раз меняет свое направление при переходе через нулевое значение.

Лампы, включенные в сеть, сто раз в секунду притухают и столько же раз вспыхивают ярче, но глаз этого не замечает, благодаря зрительной инерции, т. е. способности сохранять полученные впечатления около 0,1 с.

При расчетах с переменными токами пользуются также угловой частотой, она равна 2пиf или 6,28f. Ее следует выражать не в герцах, а в радианах в секунду.

В современных генераторах переменного тока вращается их магнитная система, а проводники, в которых индуктируется э.д.с, размещаются в неподвижной части машины.

Переменные токи принято разделять по частоте. Токи с частотой меньше 10000 Гц называют токами низкой частоты (токами НЧ).

У этих токов частота соответствует частоте различных звуков человеческого голоса или музыкальных инструментов, и поэтому они иначе называются токами звуковой частоты (за исключением токов с частотой ниже 20 Гц, которые не соответствуют звуковым частотам). В радиотехнике токи НЧ имеют большое применение, особенно в радиотелефонной передаче.

Однако главную роль в радиосвязи выполняют переменные токи с частотой более 10000 Гц, называемые токами высокой частоты, или радиочастоты (токи ВЧ).

Для измерения частоты этих токов применяют единицы: килогерц (кГц), равный тысяче герц, мегагерц (МГц), равный миллиону герц, и гигагерц (ГГц), равный миллиарду герц. Иначе килогерц, мегагерц и гигагерц обозначают kHz, MHz, GHz. Токи частотой в сотни мегагерц и выше называют токами сверхвысокой или ультравысокой частоты (СВЧ и УВЧ).

Радиостанции работают с помощью переменных токов ВЧ, имеющих частоту от сотен килогерц и выше. В современной радиотехнике для специальных целей применяются токи с частотой в миллиарды герц и имеются приборы, позволяющие точно измерять такие сверхвысокие частоты.

Источник

Период, частота, амплитуда и фаза переменного тока

Период и частота переменного тока

Время, в течение которого совершается одно полное изме­нение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания пере­менного тока (рисунок 1).

Период выражают в секундах и обозначают буквой Т.

Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.

Число полных изменений ЭДС или число оборотов ради­уса-вектора, то есть иначе говоря, число полных циклов колеба­ний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.

Частота обо­значается буквой f и выражается в периодах в секунду или в герцах.

Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.

1000 Гц = 10 3 Гц = 1 кГц;

1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Чем быстрее происходит изменение ЭДС, то есть чем бы­стрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.

Математическая связь между периодом и частотой переменного тока и напряжения выра­жается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

Т = 1/f = 1/50 = 0,02 сек.

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:

f = 1/T=1/0,02 = 100/2 = 50 Гц

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Частоты от 20 до 20 000 Гц называются звуковыми часто­тами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие вы­сокие частоты называются радиочастотами или колебаниями высокой частоты.

Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.

Амплитуда переменного тока

Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно бук­вами Im, Em и Um (рисунок 1).

Угловая (циклическая) частота переменного тока.

Скорость вращения радиуса-вектора, т. е. изменение ве­личины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (оме­га). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.

Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.

Рисунок 2. Радиан.

1рад = 360°/2

? = 6,28*f = 2f

Фаза переменного тока.

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза пока­зывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.

Полный оборот радиуса-вектора равен 360°. С началом но­вого оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следова­тельно, все фазы ЭДС будут повторяться в прежнем поряд­ке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обо­их этих случаях радиус-вектор занимает одинаковое положе­ние, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Источник

Период, частота, амплитуда и фаза переменного тока

Что такое переменное напряжение?

Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.

Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.

Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид

Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда

Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже

Синусоидальное переменное напряжение.

Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.

Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением

где Um – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла),

φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.

Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.

Таким образом, амплитуда Um, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.

Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда

В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.

Переменный ток. Изображение синусоидальных переменных.

Представление синусоидальных величин с помощью векторов и комплексных чисел

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими,

а наименьший промежуток времени, через который эти повторения наблюдаются, —
периодом Т.
Для периодического тока имеем

Величина, обратная периоду, есть частота,

измеряемая в герцах (Гц):

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

— мгновенное значение тока ;

мгновенное значение напряжения ;

— мгновенное значение ЭДС ;

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).

Действующее значение переменного тока

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1

и
е2
соответствуют уравнения:

Значения аргументов синусоидальных функций и называются фазами

синусоид, а значение фазы в начальный момент времени
(t=0):
и —
начальной фазой
( ).

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз

Для синусоидальных ЭДС е1

Векторное изображение синусоидально
изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное

) с угловой частотой, равной
w
. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС
е1
и
е2
(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют
векторными диаграммами.
При построении векторных диаграмм векторы удобно располагать для начального момента времени
(t=0),
что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью
w
. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

Результирующий ток также будет синусоидален:

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t=0.

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Представление синусоидальных ЭДС, напряжений и токов комплексными числами

Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :

Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как

В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:

Комплексное число удобно представить в виде произведения двух комплексных чисел:

(или на вращающейся со скоростью
w
комплексной плоскости), называют
комплексной амплитудой:
, а параметр —
комплексом мгновенного значения.
Параметр является оператором поворота

вектора на угол
wt
относительно начального положения вектора.

Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ±a

Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j”

произведения комплекса амплитуды и оператора поворота :

Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:

Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:

Тогда мгновенное значение напряжения:

а при (третий квадрант)

Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.

Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:

Действующее значение синусоидальных ЭДС, напряжений и токов

В соответствии с выражением (3) для действующего значения синусоидального тока запишем:

Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз:

Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения

Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?

2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?

3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?

4. Для заданных синусоидальных функций ЭДС и тока записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.

Что такое действующее напряжение переменного тока?

Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?

Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения

Для переменного напряжения мгновенное значение выделяемой энергии составит

где u – мгновенное значение напряжения

Тогда количество энергии за полный период от t0 = 0 до t1 = T составит

Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения

Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.

Действующее значение синусоидального напряжения.

Вычислим действующее значение синусоидального напряжения

Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.

Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение

Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения

Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.

С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.

Постоянный и переменный электрический ток

Действие электрического тока состоит в том, что носители заряда движутся по цепи под действием электрического поля источника тока и совершают работу на сопротивлении нагрузки (энергия при этом выделяется в виде тепла). Исторически первыми источниками тока были гальванические элементы. В таких элементах электрическое поле не меняет направление. В цепи, подключенной к гальваническому элементу, носители движутся также в одном направлении.

Рис. 1. Гальванические элементы.

Однако это не единственная возможность движения носителей. Носители могут не совершать поступательное движение, а колебаться вокруг некоторого среднего положения. При этом на сопротивлении нагрузки также будет выделяться мощность.

Электрический ток, в котором носители заряда движутся в одном направлении, называется постоянным. Если носители заряда не движутся в одном направлении, а совершают гармонические колебания вокруг некоторого среднего положения, такой электрический ток называется переменным.

Рис. 2. Постоянный и переменный ток.

Что такое среднее значение переменного напряжения?

Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением

где Т – период переменного напряжения,

fu(t) – функциональная зависимость напряжения от времени.

Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.

Среднее значение переменного напряжения.

В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.

Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно

где Um – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла).

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая “пробивает пол” берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

выпрямленное переменное напряжение после диодного моста

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Источник