Что такое период кристаллической решетки
Период кристаллической решетки
Для самой простой идеальной одноатомной кубической решетки это просто расстояние между соседними атомами. В общем случае — это наименьшее расстояние, при сдвиге на которое решетка точно воспроизводит свой исходный вид, то есть в каждом ее узле оказываются такие же атомы, что и до сдвига.
Смотреть что такое «Период кристаллической решетки» в других словарях:
Период кристаллической решётки — длина ребра элементарной ячейки кристаллической решётки. Для самой простой идеальной одноатомной кубической решетки это просто расстояние между соседними атомами. В общем случае это наименьшее расстояние, при сдвиге на которое решетка точно… … Википедия
Первый период периодической системы — К первому периоду периодической системы относятся элементы первой строки (или первого периода) периодической системы химических элементов. Строение периодической таблицы основано на строках для иллюстрации повторяющихся (периодических) трендов в… … Википедия
КРИСТАЛЛИЧЕСКАЯ РЕШЕТКА — – характерное для равновесного состояния твердого тела (кристалла) расположение атомов (ионов), обладающих периодической повторяемостью в пространстве. У магнитных минералов период кристаллической решетки – элементарная ячейка – менее 1нм. Для… … Палеомагнитология, петромагнитология и геология. Словарь-справочник.
Брэгг, Уильям Генри — Уильям Генри Брэгг англ. William Henry Bragg Да … Википедия
Кость — I Кость (os) орган опорно двигательного аппарата, построенный преимущественно из костной ткани. Совокупность К., связанных (прерывно или непрерывно) соединительной тканью, хрящом или костной тканью, образует Скелет. Общее количество К. скелета… … Медицинская энциклопедия
Геомодификаторы трения — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/28 ноября 2012. Пока процесс обсуждени … Википедия
Горная порода — (Rock) Горная порода это совокупнность минералов, образующая самостоятельное тело в земной коре, вследстие природных явлений Группы горных пород, магматические и метаморфические горные породы, осадочные и метасоматические горные породы, строение… … Энциклопедия инвестора
Борн, Макс — У этого термина существуют и другие значения, см. Борн. Макс Борн Max Born … Википедия
Металл — (Metal) Определение металла, физические и химические свойства металлов Определение металла, физические и химические свойства металлов, применение металлов Содержание Содержание Определение Нахождение в природе Свойства Характерные свойства… … Энциклопедия инвестора
Электронная библиотека
Кристаллическую решетку характеризуют следующие основные параметры:
· базис и коэффициент компактности решетки.
Под атомным радиусом понимают половину межатомного расстояния между центрами ближайших атомов в кристаллической решетке элемента при нормальной температуре и атмосферном давлении. Однако атомный радиус не является постоянной величиной, а изменяется в зависимости от ряда факторов, важнейшими из которых являются координационное число и тип химической связи между атомами в кристалле.
Энергия кристаллической решетки определяется как энергия, выделяющаяся при образовании кристалла из ионов, атомов или других частиц, образующих кристалл, когда исходное состояние этих частиц газообразное. От величины энергии решетки зависят такие свойства вещества, как температура плавления, модуль упругости, прочность, твердость и др. Увеличение валентности атомов приводит к увеличению энергии решетки.
Координационное число (К), показывает количество атомов, находящихся на наиболее близком и равном расстоянии от любого выбранного атома в решетке.
Базисом решетки называется количество атомов, приходящихся на одну элементарную ячейку решетки.
Коэффициент компактности (?) решетки определяется отношением объема, занимаемого атомами (Va), ко всему объему решетки (Vp), т.е.
? = Va/Vp. Представленные на рис. 1.2 (сверху) типы кристаллических решеток схематично отражают взаимное расположение атомов (ионов) в кристалле. Если условно считать атомы шарами одинакового диаметра, то снизу на рис. 1.2 дано более точное представление о действительном расположении атомов в кристаллах ОЦК, ГЦК и ГПУ
Пример: Гранецентрированная кубическая решетка (рис. 1.2, б) имеет восемь атомов по вершинам и по одному атому в центре граней куба. Определим для нее такие понятия, как «координационное число» и «базис» решетки.
Оперируя с элементарной ячейкой, нельзя забывать, что в реальном кристалле такая ячейка окружена со всех сторон другими ячейками и поэтому не все атомы, отно
сящиеся к рассматриваемой ячейке, принадлежат только этой ячейке. Для того чтобы это понять, рекомендуется изобразить на клетчатой бумаге элементарную ячейку и пристроить к ней со всех сторон другие ячейки. Важность такого построения выявляется при решении конкретных задач.
Из рис. 1.2, б видно, что минимальное расстояние между атомами в решетке ГЦК равно половине диагонали грани. Пристроив около какой-либо вершины куба другие примыкающие к ней ячейки, подсчитаем координационное число: к любой вершине куба реально пристроены 8 элементарных ячеек; в каждой ячейке на расстоянии η диагонали грани находится три атома; каждая грань обслуживает две ячейки, поэтому
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Кристаллическая решетка
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Что такое кристаллическая решетка
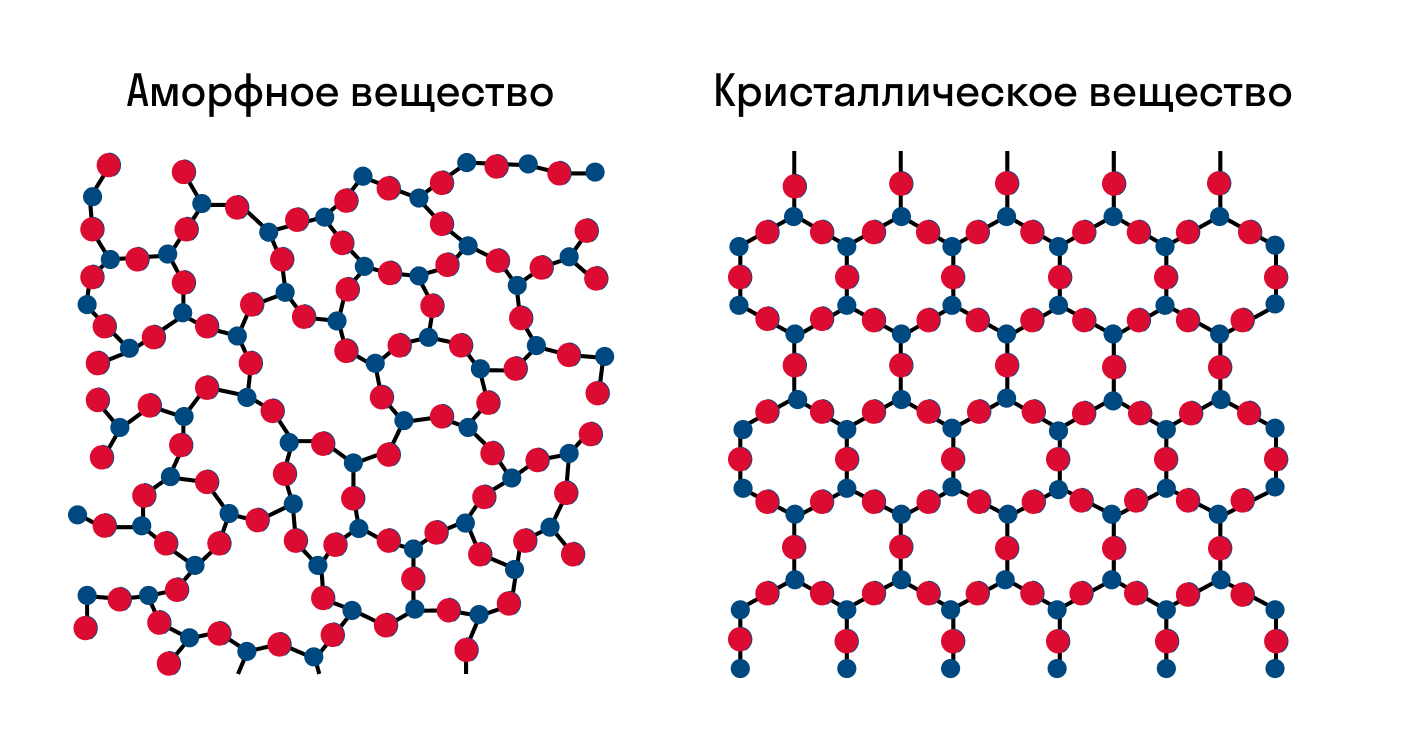
Как известно, все вещества состоят из частиц — атомов, которые могут располагаться хаотично или в определенном порядке. У аморфных веществ частицы расположены беспорядочно, а у кристаллических они образуют определенную структуру. Эта структура называется кристаллической решеткой. Она определяет такие характеристики вещества, как твердость, хрупкость, температура кипения и/или плавления, пластичность, растворимость, электропроводность и т. д.
Кристаллическая решетка — это внутренняя структура кристалла, порядок взаимного расположения атомов, ионов или молекул. Точки, в которых находятся эти частицы, называются узлами решетки.
Частицы удерживаются на своих местах благодаря химическим связям между ними. В зависимости от того, какой вид связи удерживает атомы или ионы данного вещества, в химии выделяют основные типы кристаллических решеток:
атомная (ковалентные связи),
молекулярная (ковалентные связи и притяжение между молекулами),
металлическая (металлические связи),
ионная (ионные связи).
Строение и агрегатное состояние веществ
Выделяют три агрегатных состояния: твердое тело, жидкость и газ. Каждое из них предполагает определенное расположение частиц. Ниже мы расскажем подробнее, как связаны в химии кристаллическая решетка и агрегатное состояние вещества, а пока осветим общие закономерности.
Если частицы хаотично движутся, а расстояние между ними многократно превышает их собственные размеры — это газ. За счет большой удаленности друг от друга молекулы и атомы в таком веществе слабо взаимодействуют между собой.
Если частицы расположены все так же беспорядочно, но на небольшом расстоянии друг от друга — это жидкость. В жидком состоянии вещества его молекулы и атомы имеют более прочные связи, которые сложнее разорвать.
Если частицы собраны близко друг к другу и в определенном порядке — это твердое тело. В таком состоянии связи между ними наиболее прочны. Частицы могут двигаться только в пределах своего расположения и почти не перемещаются в пространстве.
Большинство веществ могут находиться и в твердом, и в жидком, и газообразном состоянии, а в зависимости от давления и температуры легко переходить из одного в другое. Типичный пример — вода, которая при нагревании превращается в пар, а при остывании становится твердым льдом.
Атомная кристаллическая решетка
Согласно своему названию, атомная кристаллическая решетка — это структура, в узлах которой расположены атомы. Они взаимодействуют с помощью ковалентных связей, то есть один атом отдает другому свободный электрон или же электроны из разных атомов образуют общую пару. В кристаллах с атомной решеткой частицы прочно связаны, что обуславливает ряд физических характеристик.
Свойства веществ с атомной решеткой:
неспособность к растворению в воде,
высокая температура кипения и плавления.
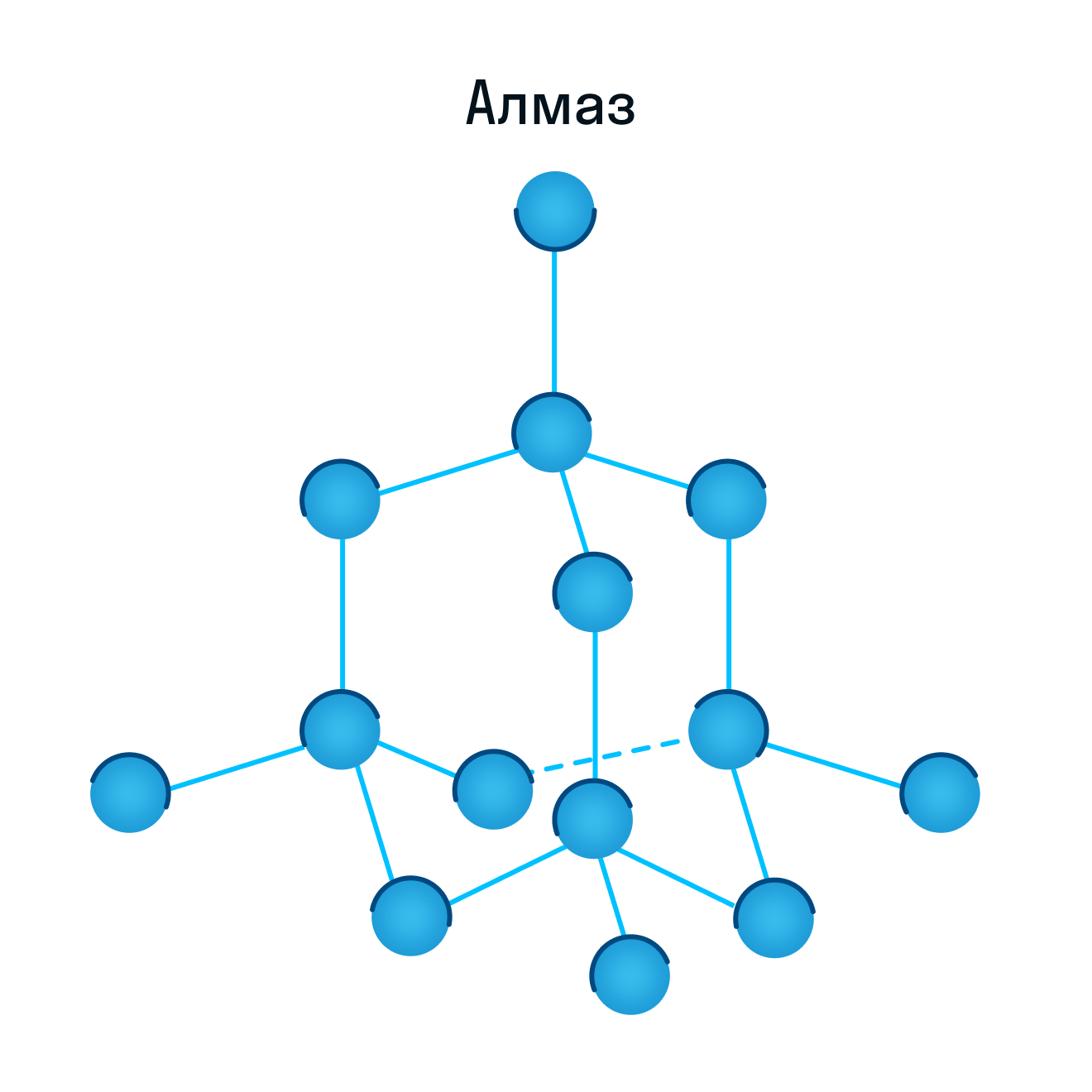
К примеру, атомную кристаллическую решетку имеет алмаз — самый твердый минерал в мире.
Другие примеры: германий Ge, кремний Si, нитрид бора BN, карборунд SiC. Типичный представитель этой группы — обычный песок, который по сути является оксидом кремния SiO2.
Молекулярная кристаллическая решетка
Как и в предыдущей группе, в этой находятся вещества с ковалентными связями между атомами. Но физические характеристики этих веществ совершенно иные — они легко плавятся, превращаются в жидкость, растворяются в воде. Почему так происходит? Все дело в том, что здесь кристаллы строятся не из атомов, а из молекул.
Молекулярная кристаллическая решетка — это структура, в узлах которой находятся не атомы, а молекулы.
Внутри молекул атомы имеют прочные ковалентные связи, но сами молекулы связаны между собой слабо. Поэтому кристаллы таких веществ непрочные и легко распадаются.
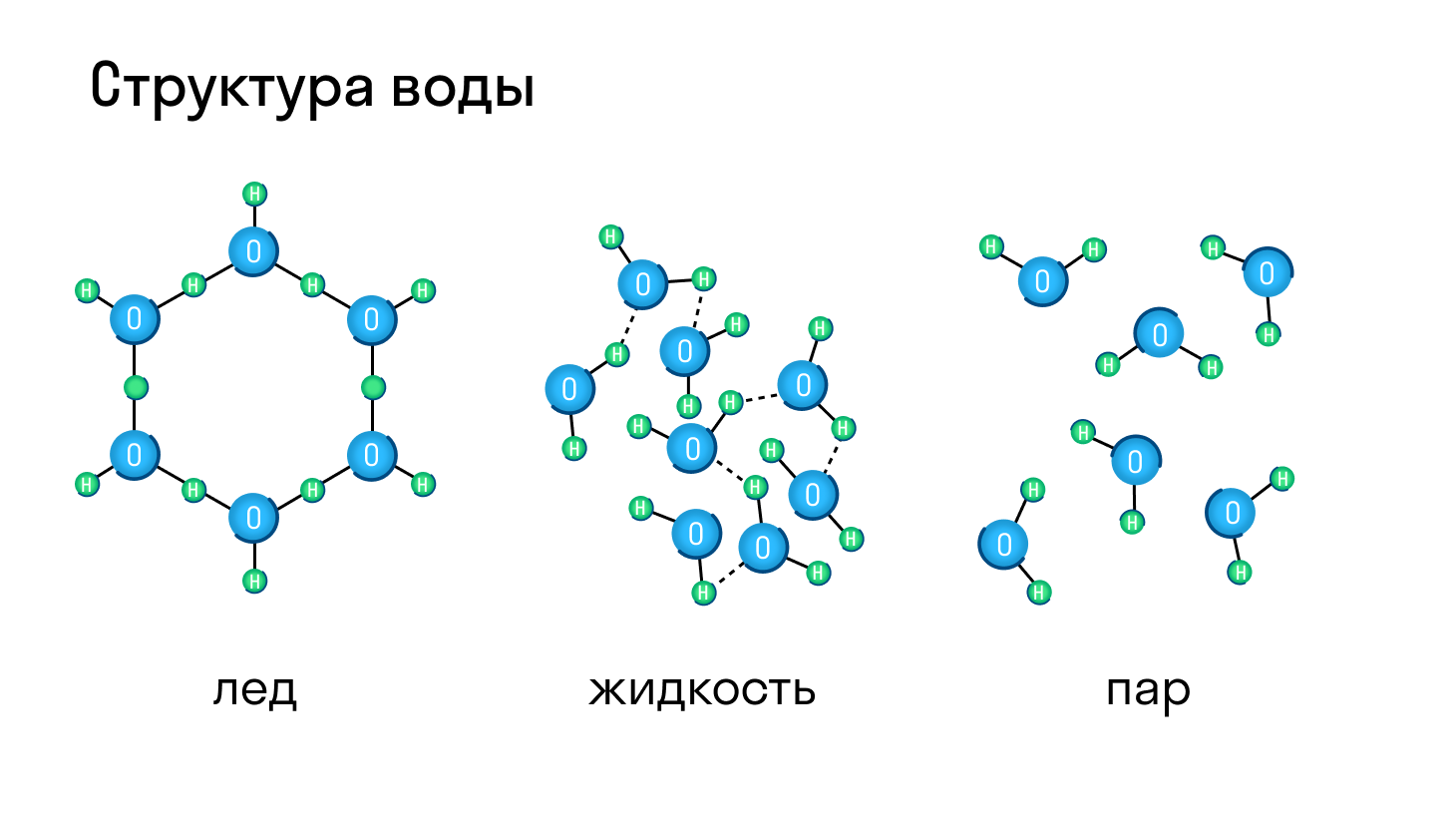
Молекулярная кристаллическая решетка характерна для воды. При комнатной температуре это жидкость, но стоит нагреть ее до температуры кипения (которая сравнительно низка), как она тут же начинает превращаться в пар, т. е. переходит в газообразное состояние.
Некоторые молекулярные вещества — например, сухой лед CO2, способны преобразоваться в газ сразу из твердого состояния, минуя жидкое (данный процесс называется возгонкой).
Свойства молекулярных веществ:
у некоторых — наличие запаха.
Помимо воды к веществам с молекулярной кристаллической решеткой относятся аммиак NH3, гелий He, радон Rn, йод I, азот N2 и другие. Все благородные газы — молекулярные вещества. Также к этой группе принадлежит и большинство органических соединений (например, сахар).
Ионная кристаллическая решетка
Как известно, в ходе ионной химической связи один атом отдает другому ионы и приобретает положительный заряд, в то время как принимающий атом заряжается отрицательно. В итоге появляются разноименно заряженные ионы, из которых и состоит структура кристалла.
Ионная решетка — это кристаллическая структура, в узловых точках которой находятся ионы, связанные взаимным притяжением.
Ионную кристаллическую решетку имеют практически все соли, типичным представителем можно считать поваренную соль NaCl. О ней стоит вспомнить, если нужно перечислить физические характеристики этой группы. Также ионную решетку имеют щелочи и оксиды активных металлов.
Свойства веществ с ионной структурой:
способность растворяться в воде.
Примеры веществ с ионной кристаллической решеткой: оксид кальция CaO, оксид магния MgO, хлорид аммония NH4Cl, хлорид магния MgCl2, оксид лития Li2O и другие.
Металлическая кристаллическая решетка
Для начала вспомним, как проходит металлическая химическая связь. В молекуле металла свободные отрицательно заряженные электроны перемещаются от одного иона к другому и соединяются с некоторыми из них, а после отрываются и мигрируют дальше. В результате получается кристалл, в котором ионы превращаются в атомы и наоборот.
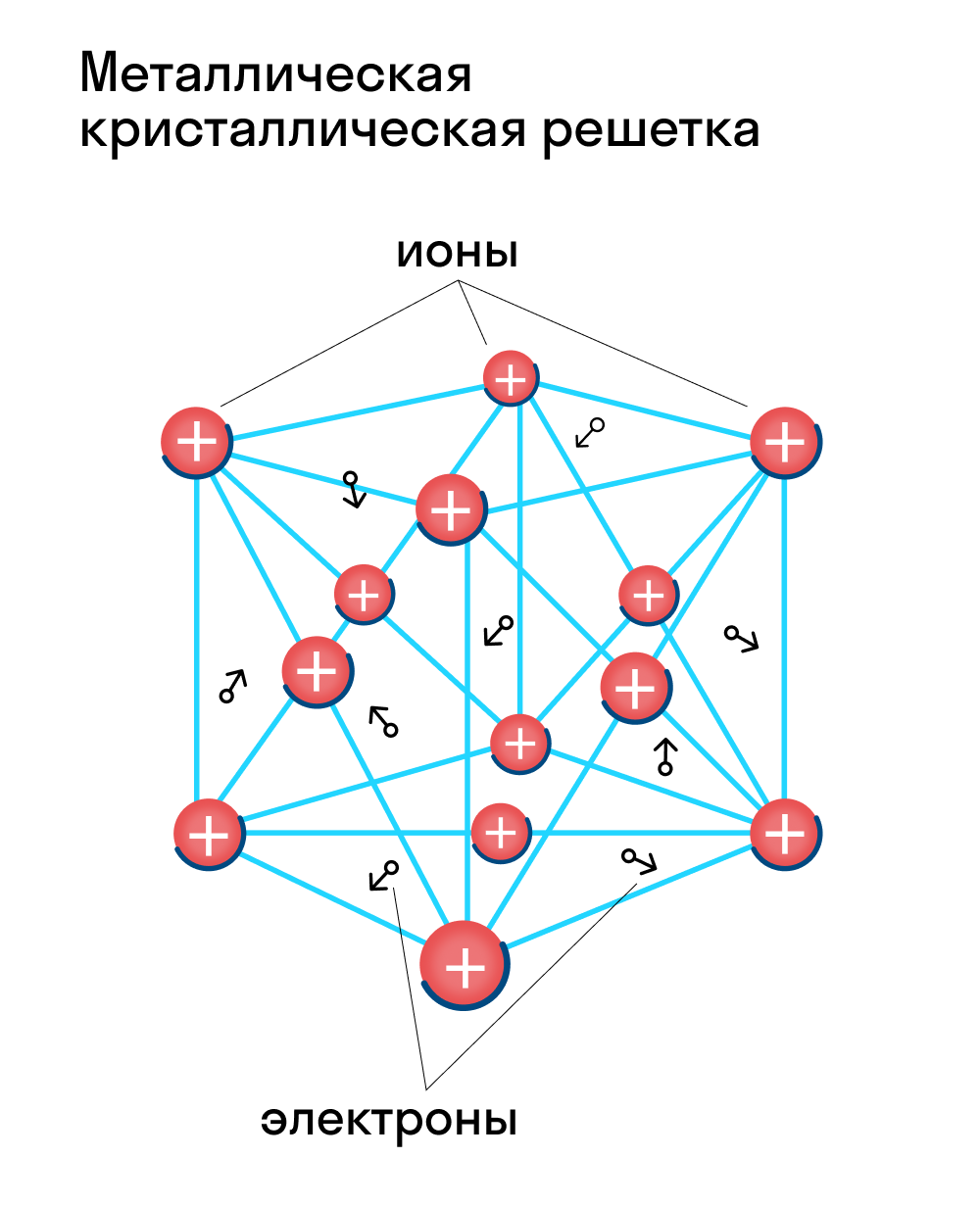
Металлическая кристаллическая решетка — это структура, которая состоит из ионов и атомов металла, а между ними свободно передвигаются электроны. Как несложно догадаться, она характерна лишь для металлов и сплавов.
Свободные электроны, мигрирующие между узлами решетки, образуют электронное облако, которое под воздействием электротока приходит в направленное движение. Это объясняет такое свойство металлов, как электрическая проводимость.
В химии типичным примером вещества, которое имеет металлическую кристаллическую решетку, считается медь. Она очень ковкая, пластичная, имеет высокую тепло- и электропроводность. Впрочем, все металлы ярко демонстрируют эти характеристики, поэтому назвать физические свойства данной группы несложно.
Свойства веществ с металлической кристаллической решеткой:
При этом температура плавления веществ может существенно различаться. Например, у ртути это −38,9°С, а у бериллия целых +1287°С.
Подведем итог: о характеристиках разных типов кристаллических решеток расскажет таблица.
Частицы в узлах решетки
Тип связи между частицами
Физические свойства веществ
Как определить кристаллическую решетку
Как понятно из предыдущего материала, строение вещества, его состав и физические характеристики тесно связаны. Поэтому для определения вида кристаллической решетки можно руководствоваться теми данными, которые у нас есть. Как правило, известен состав вещества, а значит, мы можем сделать вывод о химических связях внутри его молекулы, что позволит в свою очередь предположить тип решетки.
Также можно провести быстрый анализ:
если это неметалл, который при комнатной температуре представляет собой твердое тело — скорее всего он имеет атомную решетку;
если в обычных условиях это жидкость или газ либо речь об органическом веществе — предполагаем молекулярную решетку;
если это соль либо щелочь — кристаллы имеют ионную решетку;
если это металл или сплав — решетка точно будет металлической.
Вопросы для самопроверки:
Назовите виды кристаллических решеток.
Чем отличается кристаллическая решетка от химической связи?
Назовите примеры веществ с металлической кристаллической решеткой, с ионной, атомной и молекулярной.
Выберите лишнее вещество: молекулярную кристаллическую решетку имеет вода, поваренная соль, аргон, криптон.
Какое строение вещества придает ему высокую электропроводность?
Какое строение кристалла может придать веществу способность к возгонке?
Период кристаллической решётки
Для самой простой идеальной одноатомной кубической решетки это просто расстояние между соседними атомами. В общем случае — это наименьшее расстояние, при сдвиге на которое решетка точно воспроизводит свой исходный вид, то есть в каждом ее узле оказываются такие же атомы, что и до сдвига.
Смотреть что такое «Период кристаллической решётки» в других словарях:
период кристаллической решётки — kristalo gardelės konstanta statusas T sritis fizika atitikmenys: angl. crystal lattice spacing; lattice constant vok. Gitterkonstante, f; Kristallgitterabstand, m rus. период кристаллической решётки, m; период решётки кристалла, m; постоянная… … Fizikos terminų žodynas
постоянная кристаллической решётки — kristalo gardelės konstanta statusas T sritis fizika atitikmenys: angl. crystal lattice spacing; lattice constant vok. Gitterkonstante, f; Kristallgitterabstand, m rus. период кристаллической решётки, m; период решётки кристалла, m; постоянная… … Fizikos terminų žodynas
период решётки кристалла — kristalo gardelės konstanta statusas T sritis fizika atitikmenys: angl. crystal lattice spacing; lattice constant vok. Gitterkonstante, f; Kristallgitterabstand, m rus. период кристаллической решётки, m; период решётки кристалла, m; постоянная… … Fizikos terminų žodynas
Период кристаллической решетки — Период кристаллической решётки длина ребра элементарной ячейки кристаллической решётки. Для самой простой идеальной одноатомной кубической решетки это просто расстояние между соседними атомами. В общем случае это наименьшее расстояние, при сдвиге … Википедия
Второй период периодической системы — Ко второму периоду периодической системы относятся элементы второй строки (или второго периода) периодической системы химических элементов. Строение периодической таблицы основано на строках для иллюстрации повторяющихся (периодических) трендов в … Википедия
Полупроводниковые материалы — Для улучшения этой статьи желательно?: Викифицировать статью. Полупроводниковые материалы вещества с чётко в … Википедия
Gitterkonstante — kristalo gardelės konstanta statusas T sritis fizika atitikmenys: angl. crystal lattice spacing; lattice constant vok. Gitterkonstante, f; Kristallgitterabstand, m rus. период кристаллической решётки, m; период решётки кристалла, m; постоянная… … Fizikos terminų žodynas
Kristallgitterabstand — kristalo gardelės konstanta statusas T sritis fizika atitikmenys: angl. crystal lattice spacing; lattice constant vok. Gitterkonstante, f; Kristallgitterabstand, m rus. период кристаллической решётки, m; период решётки кристалла, m; постоянная… … Fizikos terminų žodynas
constante du réseau cristallin — kristalo gardelės konstanta statusas T sritis fizika atitikmenys: angl. crystal lattice spacing; lattice constant vok. Gitterkonstante, f; Kristallgitterabstand, m rus. период кристаллической решётки, m; период решётки кристалла, m; постоянная… … Fizikos terminų žodynas
crystal lattice spacing — kristalo gardelės konstanta statusas T sritis fizika atitikmenys: angl. crystal lattice spacing; lattice constant vok. Gitterkonstante, f; Kristallgitterabstand, m rus. период кристаллической решётки, m; период решётки кристалла, m; постоянная… … Fizikos terminų žodynas
Кристаллическая решетка
Кристалли́ческая решётка — пространственное периодическое расположение атомов или ионов в кристалле. Для описания кристаллической решётки достаточно знать расположение частиц в элементарной ячейке кристалла, повторением которой образуется вся кристаллическая решётка.
Содержание
Общая характеристика
Существует огромное количество кристаллических структур. Их объединяет главное свойство кристаллического состояния вещества — закономерное положение атомов в кристаллической решётке. Одно и то же вещество может кристаллизоваться в разных кристаллических решётках и обладать весьма различными свойствами (классический пример графит — алмаз). В случае простых веществ это явление называется аллотропией, в общем случае любых химических соединенй — полиморфизмом. В то же время, разные вещества могут образовывать однотипные, или изоморфные, решётки, как, например, решётки многих металлов: меди, алюминия, серебра, золота. Иногда происходит замещение атомов в кристаллической решётке на атомы другого химического элемента с образованием твёрдого раствора.
В зависимости от пространственной симметрии, все кристаллические решётки подразделяются на семь кристаллических систем. По форме элементарной ячейки они могут быть разбиты на шесть сингоний. Все возможные сочетания имеющихся в кристаллической решётке поворотных осей симметрии и зеркальных плоскостей симметрии приводят к делению кристаллов на 32 класса симметрии, а с учётом винтовых осей симметрии и скользящих плоскостей симметрии на 230 пространственных групп.
Помимо основных трансляций, на которых строится элементарная ячейка, в кристаллической решётке могут присутствовать дополнительные трансляции, называемые решётками Браве. В трёхмерных решётках бывают гранецентрированная (F), объёмноцентрированная (I), базоцентрированная (A, B или C), примитивная (P) и ромбоэдрическая (трансляций состоит из множества векторов (a, b, c), во все остальные входят одна или несколько дополнительных трансляций. Так, в объёмноцентрированную систему трансляций Браве входит четыре вектора (a, b, c, ½(a+b+c)), в гранецентрированную — шесть (a, b, c, ½(a+b), ½(b+c), ½(a+c)). Базоцентрированные системы трансляций содержат по четыре вектора: A включает вектора (a, b, c, ½(b+c)), B — вектора (a, b, c, ½(a+c)), а C — (a, b, c, ½(a+b)), центрируя одну из граней элементарного объёма. В системе трансляций Браве R дополнительные трансляции возникают только при выборе гексагональной элементарной ячейки и в этом случае в систему трансляций R входят вектора (a, b, c, 1 /3(a+b+c), — 1 /3(a+b+c)).