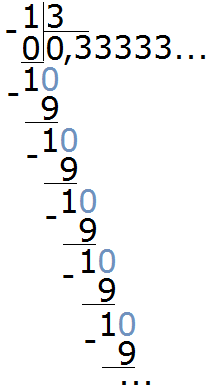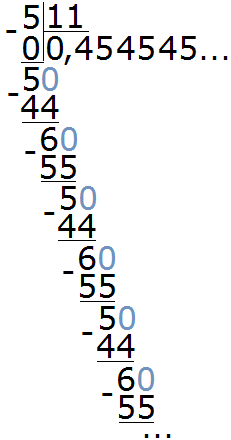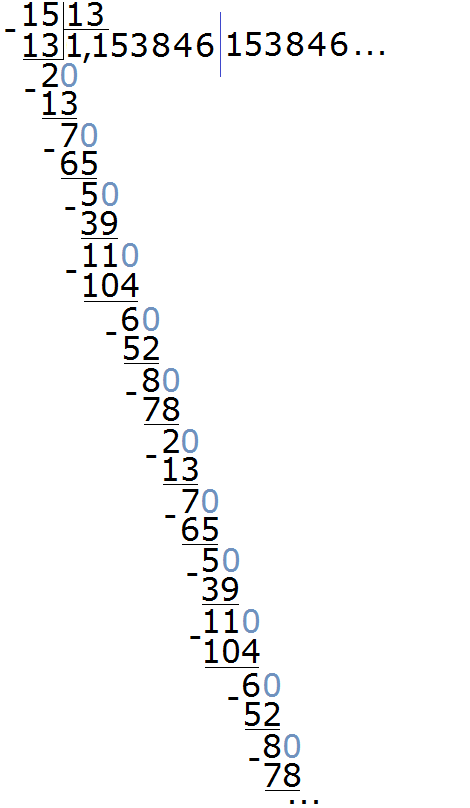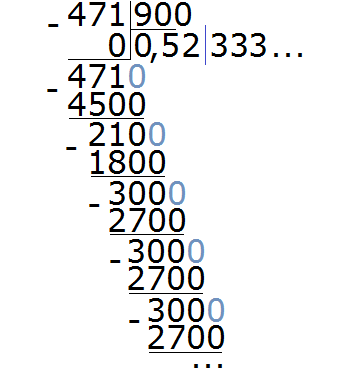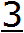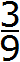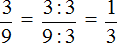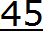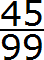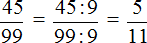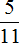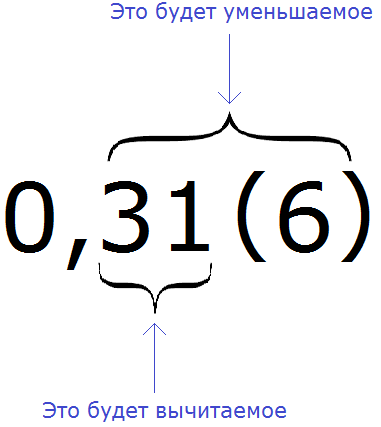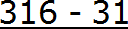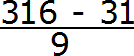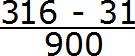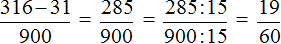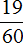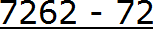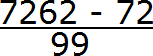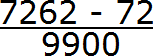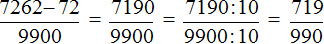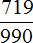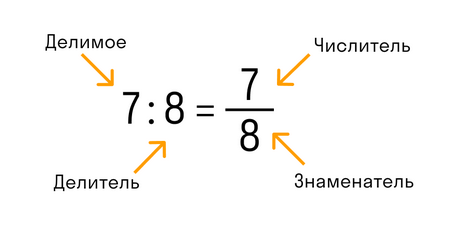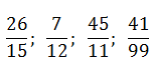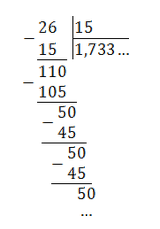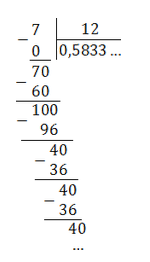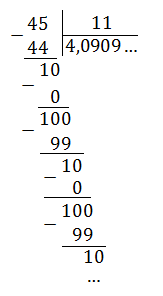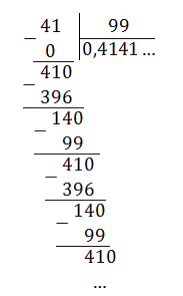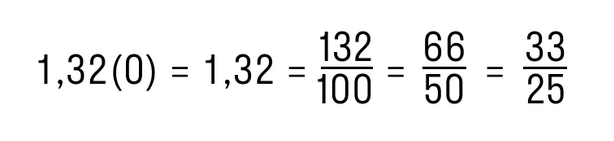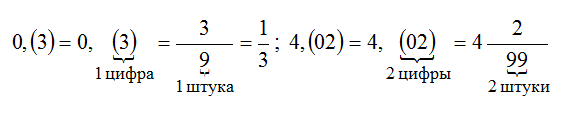Что такое период математика

ПЕРИОД

Аналогично определяется П. функции, определенной на нек-рой абелевой группе. А. А. Конюшков.

Смотреть что такое ПЕРИОД в других словарях:

ПЕРИОД

ПЕРИОД

период 1. м. 1) а) Промежуток времени, в который протекает определенная часть общего процесса. б) Время, в течение которого отлагаются осадки, образующие систему; часть эры (в геологии). в) Время между началом реакции и моментом достижения ею скорости, доступной обнаружению при эксперименте (в химии). 2) а) Промежуток времени, в течение которого совершается какой-л. повторяющийся процесс. б) Время оборота планеты или кометы (в астрономии). в) Промежуток времени, в течение которого изменяющаяся величина совершает один полный цикл своего изменения (в физике). 3) Этап общественного или культурно-исторического развития, общественного движения в жизни страны, народа. 2. м. Сложное синтаксическое построение, состоящее из одного сложного предложения или из соединения группы предложений, характеризуемое подробным развитием мысли и ритмической законченностью интонации и употребляемое как стилистический прием (в лингвистике). 3. м. Небольшое законченное построение, представляющее соединение двух предложений, одинаковых по их мелодической основе, но различных по завершению (в музыке). 4. м. Группа повторяющихся цифр в бесконечной десятичной дроби (в математике).

ПЕРИОД

период м.1. (в разн. знач.) period; (короткий тж.) spell за короткий период времени — in a short space of time 2. геол. age ледниковый период — glaci. смотреть

ПЕРИОД

ПЕРИОД

ПЕРИОД в риторике, пространное сложноподчинённое предложение, отличающееся полнотой развёртывания мысли и законченностью интонации. Полнота мысли дос. смотреть

ПЕРИОД

ПЕРИОД

ПЕРИОД в музыке, построение, излагающее законченную или относительно законченную муз. мысль. Обычно состоит из двух частей (предложений) по 4 или 8 т. смотреть

ПЕРИОД

2.18 период: Продолжительность времени. Источник: ГОСТ ИСО 8601-2001: Система стандартов по информации, библиотечному и издательскому делу. Представ. смотреть

ПЕРИОД

ПЕРИОД (греч. periodos — «обход», «окружность») — термин, введенный Аристотелем для обозначения «речи, имеющей в себе самой начало и конец и ле. смотреть

ПЕРИОД

ПЕРИОД (Περίοδος — обход, окружность). Этим словом в древней Греции называлась та замкнутая, кольцевая дорога, на которой происходили игры и состя. смотреть

ПЕРИОД

(от греч. periodos – обход, круг, круговращение) – стилистическая фигура, представляющая собой семантико-структурное единство, образованное простым или. смотреть

ПЕРИОД

ПЕРИОД

ПЕРИОД

ПЕРИОД а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та и. смотреть

ПЕРИОД

пери́од сущ., м., употр. часто Морфология: (нет) чего? пери́ода, чему? пери́оду, (вижу) что? пери́од, чем? пери́одом, о чём? о пери́оде; мн. что? пер. смотреть

ПЕРИОД

cycle, epoch связь, period, run, (десятичной дроби) repetend, season, stage, periodic time* * *пери́од м. 1. (периодических явлений) period; (интервал. смотреть

ПЕРИОД

ПЕРИОД

[греч. periodos — «обход», «окружность»]— термин, введенный Аристотелем для обозначения «речи, имеющей в себе самой начало и конец и легко обнимаемой умом». Под П. следует понимать так. обр. большую синтаксическую единицу, сложное предложение или группу предложений, характеризуемую полнотой выражения мысли и законченностью интонации, создаваемой выделением пауз, сменой повышения и понижения, замедления и ускорения речи, ритмическим движением клаузулы. Пример: «Как плавающий в небе ястреб, давший много кругов сильными крылами, вдруг останавливается распластанный среди воздуха на одном месте и бьет оттуда стрелой на раскричавшегося у самой дороги самца-перепела: так Тарасов сын Остап налетел вдруг на хорунжего и сразу накинул ему на шею веревку» (Гоголь). Античная и школьная риторика с большой тщательностью разрабатывает учение о П. Устанавливаются классификации П.: 1. по числу входящих в П. членов (membrum) или колонов (П. одночленный, двучленный, трехчленный и т. д.); 2. по соотношению величины его членов (П. умеренный, или «круглый», при равной величине его членов и П. «зыблющийся» при резком их несоответствии); 3. по наличию или отсутствию связующих союзов между членами П. (П. «слитные» и П. «отрывные»); 4. наконец по характеру этих связей. Вырабатывается вопросник для развертывания предложения в период: quis (кто), quid (что сделал), ubi (где), quibus auxilius (какими средствами), cur (для чего), quo modo (как), quando (когда). В этом плане учение о П. развертывается напр. у Готтшеда и Ломоносова. Новейшие стилистики, напротив, стремятся уловить в разнообразных вариантах П. специфическую его структурность, устанавливая в его дихотомичности, двудольности, в ритмическом и интонационном его движении известное соответствие структуре строфы (Р. Мейер, Альбала, Беккер). Многообразные виды периода в истории европейских яз. получают особое развитие в тесной связи с развитием ораторского искусства, судебного и политического красноречия в государственных образованиях античной формации (см. «Греческий яз.», «Латинский яз.»). В этот же период получает свое оформление теоретическое учение о периоде. Как учение о П., так и практика периодической речи как стилевой принадлежности произведений на латинском яз. переживают и феодальную эпоху. Эпоха строительства национальных лит-ых языков способствует переносу классического П. в церковное, научное и судебное красноречие и в стиль художественной лит-ры капиталистического общества. С окончательным оформлением «национальных» лит-ых яз. буржуазии в лит-ых стилях новейшего времени классический, определенный в своем строении и интонационно-ритмическом движении П. уступает место развернутым синтаксическим единицам иного типа, дающим больший простор индивидуальной интонации и ритму. Само по себе большее или меньшее преобладание развернутых синтаксических конструкций в яз. писателя, разумеется, ни в какой мере не позволяет определить его стиль, и лишь конкретный анализ используемых им интонационных и ритмических ходов при включении его в общий анализ писательского стиля может быть использован как один из моментов определения исторического значения последнего. Библиография: См. «Риторика», «Стилистика». R. S. смотреть

ПЕРИОД

-а, м. 1.Промежуток времени в развитии чего-л., характеризующийся теми или иными признаками, особенностями.Зимний период. Инкубационный период. Перехо. смотреть

Источник

Периодические дроби

Существуют дроби, у которых в дробной части некоторые цифры бесконечно повторяются. Выглядят эти дроби следующим образом:

Дроби такого вида называют периодическими. В данном уроке мы попробуем разобраться, что это за дроби и как с ними работать.

Получаем периодическую дробь

Попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в теме деление меньшего числа на большее. Продвинутый уровень.

Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется вновь и вновь. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разýмнее будет остановиться на достигнутом.

Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять из одной как в нашем примере.

В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).

В нашем примере повторяется цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:

Читается как «ноль целых и три в периоде»

Пример 2. Разделить 5 на 11

Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:

Читается как «ноль целых и сорок пять в периоде»

Пример 3. Разделить 15 на 13

Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:

Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».

Пример 4. Разделить 471 на 900

В этом примере период начинается не сразу, а после цифр 5 и 2. Сокращённая запись для данной периодической дроби будет выглядеть так:

Читается как: «ноль целых пятьдесят две сотых и три в периоде».

Виды периодических дробей

Периодические дроби бывают двух видов: чистые и смéшанные.

Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют чистой. Например, следующие периодические дроби являются чистыми:

Видно, что в этих дробях период начинается сразу после запятой.

Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют смéшанной. Например, следующие периодические дроби являются смéшанными:

Видно, что в этих дробях период начинается не сразу, а после некоторого количества не повторяющихся цифр.

Избавляемся от хвоста

Подобно тому, как ящерица избавляется от хвоста, мы можем избавить периодическую дробь от повторяющегося периода. Для этого достаточно округлить эту периодическую дробь до нýжного разряда.

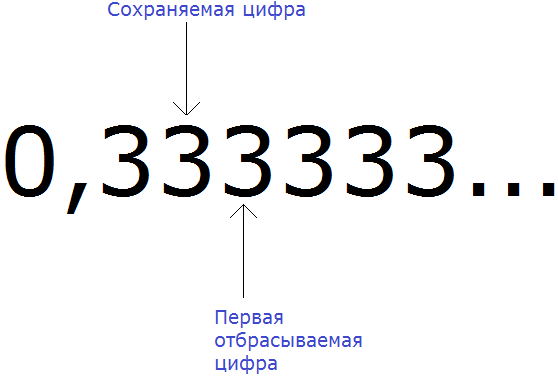
Например, округлим периодическую дробь 0, (3) до разряда сотых. Чтобы увидеть сохраняемую и отбрасываемую цифру, временно запишем дробь 0, (3) не в сокращённом виде, а в полном:

Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит периодическая дробь 0, (3) при округлении до сотых обращается в дробь 0,33

Округлим периодическую дробь 6,31 (6) до разряда тысячных.

Запишем эту дробь в полном виде, чтобы увидеть сохраняемую и отбрасываемую цифру:

Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит периодическая дробь 6,31 (6) при округлении до тысячных обращается в дробь 6,317

Перевод чистой периодической дроби в обыкновенную дробь

Перевод периодической дроби в обыкновенную это операция, которую мы будем применять довольно редко. Тем не менее, для общего развития желательно изучить и этот момент. А начнём мы с перевода чистой периодической дроби в обыкновенную дробь.

Мы уже говорили, что если период в периодической дроби начинается сразу после запятой, то такую дробь называют чистой.

Чтобы перевести чистую периодическую дробь в обыкновенную дробь, нужно в числитель обыкновенной дроби записать период периодической дроби, а в знаменатель обыкновенной дроби записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби.

В качестве примера, рассмотрим чистую периодическую дробь 0, (3) — ноль целых и три в периоде. Попробуем перевести её в обыкновенную дробь.

Правило гласит, что в первую очередь в числитель обыкновенной дроби нужно записать период периодической дроби.

Итак, записываем в числителе период дроби 0, (3) то есть тройку:

А в знаменатель нужно записать некоторое количество девяток. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (3).

В периодической дроби 0, (3) период состоит из одной цифры 3. Значит в знаменателе обыкновенной дроби записываем одну девятку:

Полученную дробь можно сократить на 3, тогда получим следующее:

Получили обыкновенную дробь .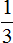

Таким образом, при переводе периодической дроби 0, (3) в обыкновенную дробь получается

Пример 2. Перевести периодическую дробь 0, (45) в обыкновенную дробь.

Здесь период составляет две цифры 4 и 5. Записываем эти две цифры в числитель обыкновенной дроби:

А в знаменатель записываем некоторое количество девяток. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0, (45).

В периодической дроби 0, (45) период состоит из двух цифр 4 и 5. Значит в знаменателе обыкновенной дроби записываем две девятки:

Полученную дробь 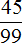можно сократить эту дробь на 9, тогда получим следующее:

Таким образом, при переводе периодической дроби 0, (45) в обыкновенную дробь получается

Перевод смешанной периодической дроби в обыкновенную дробь

Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.

В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.

Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:

Итак, записываем в числителе разность:

А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)

В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:

Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:

Получили выражение, которое вычисляется легко:

Получили ответ

Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается

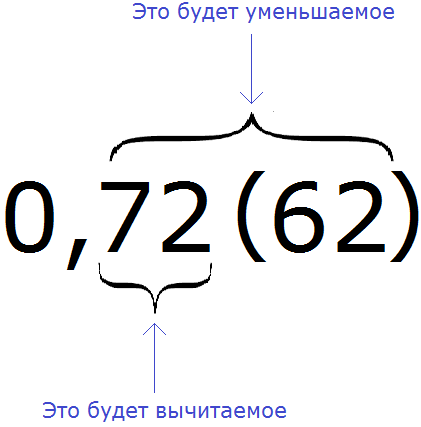
Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь

Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:

Итак, записываем в числителе разность:

А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)

В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:

Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:

Получили выражение, которое вычисляется легко:

Получили ответ

Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

34 thoughts on “Периодические дроби”

Когда же следующие уроки? Уже что-то долго ничего нету

Большое спасибо за урок! Откровенно говоря…эту тему не помню вообще…Будто ее и не было в школе О__о Ну или я ее проболела… (Перевод смешанной периодической дроби в обыкновенную дробь)

Вы бы хоть номер кошелька написали. А то столько трудились и никакой отдачи. С такими уроками никакой экзамен не страшен.

Спасибо большое Тэла, за столь добрый отзыв 😉
Если люди получают пользу от этих уроков — это уже отдача)

Огромное Вам спасибо за уроки! Всё объясняете доступно и наглядно! На ваших уроках готовлюсь поступать на ФИТ на программиста. Хорошо бы еще алгебру выложили.)

Вы не могли бы объяснить логику алгоритма перевода периодической дроби в обычную?

Зачем в знаменателе ставятся девятки — заместно, например, округления числа, подставляемого в числитель, до последней цифры периода, и постановки степени 10 в знаменатель? Зачем, при переводе смешанной периодической дроби, производится соотв. вычитание и чем объясняется подстановка нулей и единиц в зависимости от принадлежности цифры к периоду??…

Спасибо большое за урок 🙂 Скажите пожалуйсто при округлении(когда избавляемся от хвоста) откуда знать до каких разряд надо округлять?

Вот и здесь последняя задача говорит округлить до разряда сотых,а почему не до десятых(например)?

зависит от задачи, которую решаете. Если в задаче сказано округлять до десятых, значит округляете до десятых. Если сказано округлять до сотых — округляете до сотых

Источник

Как перевести периодическую дробь

Определение дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это запись числа в математике, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

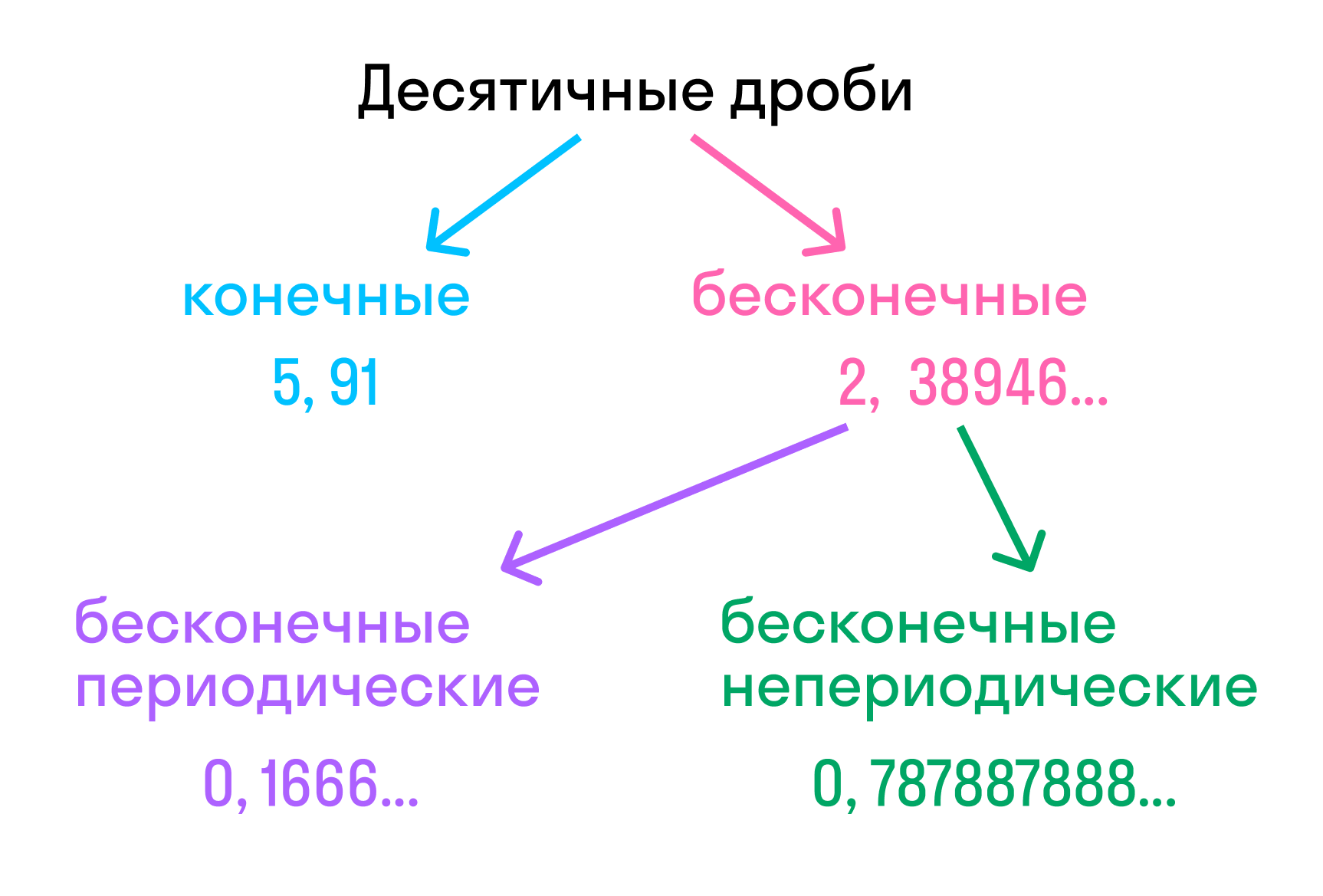
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Переход к периодической десятичной дроби

Рассмотрим обыкновенную дробь вида a/b. Разложим ее знаменатель на простые множители. Тут есть два варианта:

Чтобы задать периодическую десятичную дробь, нужно найти ее периодическую и непериодическую часть. Чтобы это сделать нужно привести дробь в неправильную, а затем разделить числитель на знаменатель столбиком.

Что будет происходить в процессе:

Повторяющиеся цифры после десятичной точки нужно обозначить периодической частью, а то, что стоит спереди — непериодической.

Пример. Перевести обыкновенные дроби в периодические десятичные:

Все дроби без целой части, поэтому просто делим числитель на знаменатель уголком:

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Определение периодической дроби

Периодическая дробь — это бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр.

Периодическая часть дроби — это набор повторяющихся цифр, из которых состоит значащая часть.

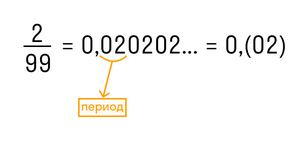
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».

Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Виды периодических дробей: чистые и смешанные.

Чистая периодическая десятичная дробь — это десятичная дробь, в записи которой сразу после запятой следует период. Например: 1,(4); 4,(25); 21,(693).

Смешанная периодическая десятичная дробь — это десятичная дробь, в записи которой после запятой через одну или несколько цифр начинается период. Например: 3,5(1); 0,02(89); 7,0(123) и т.д.

Рассмотрим примеры дробей, чтобы научиться определять части и период.

Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Читаем так: ноль целых три в периоде.

7/12 = 0,583333. = 0,58(3)

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Читаем так: ноль целых пятьдесят восемь сотых и три в периоде.

17/11 = 1,545454. = 1,(54)

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Читаем так: одна целая пятьдесят четыре сотых в периоде.

25/39 = 0,641025 641025. = 0,(641025)

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6.

Читаем так: ноль целых шестьсот сорок одна двадцать пять миллионных в периоде.

пятьдесят четыре сотых в периоде.

9200/3 = 3066,666. = 3066,(6)

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Читаем так: три тысячи шестьдесят шесть целых и шесть в периоде.

Перевод периодической дроби в обыкновенную

Давайте разберемся, как перевести периодическую десятичную дробь в обыкновенную дробь.

Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.

Пример. Преобразуем периодическую дробь 1,32(0) в обыкновенную.

Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:

Рассмотрим пример, в котором период дроби отличен от нуля.

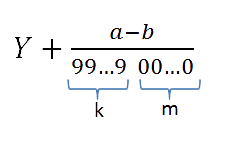
Как записать периодическую дробь 10,0219(37) в виде обыкновенной:

В нашем примере k = 2.

Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначим полученное число — a.

Теперь осталось подставить все найденные значения в формулу и получить ответ:

Вот так мы справились с задачей представить бесконечную периодическую дробь в виде обыкновенной.

Есть еще один способ преобразовать периодическую дробь в обыкновенную. Для этого нужно рассматреть периодическую часть как сумму членов геометрический прогрессии, которая убывает. Например, вот так:

Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0

Перевод чистой периодической дроби в обыкновенную

Напомним: отличие чистой периодической десятичной дроби в том, что в ней сразу после запятой следует период.

Чтобы обратить чистую периодическую дробь в обыкновенную, достаточно записать числителем ее период, а в знаменателе записать столько девяток, сколько цифр в периоде. Вот так:

Перевод смешанной периодической дроби в обыкновенную

Отличие смешанной периодической десятичной дроби в том, что после запятой через одну или несколько цифр начинается период.

Чтобы записать смешанную периодическую дробь в виде обыкновенной, нужно из числа, которое стоит до второго периода вычесть число, стоящее до первого периода, и записать результат в числителе.

А в знаменатель нужно поставить число, которое содержит столько девяток, сколько цифр в периоде, нулей в конце и сколько цифр между запятой и периодом.

Например, запишем 2,34(2) в виде обыкновенной дроби:

Источник