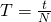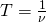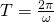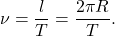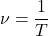Что такое период вращения в каких единицах он измеряется по какой формуле
Как сказал.
Все мы гении. Но если вы будете судить рыбу по её способности взбираться на дерево, она проживёт всю жизнь, считая себя дурой.
Альберт Эйнштейн
Вопросы к экзамену
Для всех групп технического профиля

Я учу детей тому, как надо учиться
Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.
Период вращения (обращения)
Период вращения (обращения) — это минимальное время, за которое тело совершает один полный оборот, т.е. поворачивается на угол 2π
Для нахождения периода вращения надо время всех оборотов разделить на количество оборотов:
T — период вращения
N — количество оборотов
t — время, за которое было совершено N оборотов
ν — частота вращения (обращения)
ω — угловая скорость
Законы и формулы
Сейчас 33 гостей и ни одного зарегистрированного пользователя на сайте
Спасибо тем авторам и правообладателям, которые согласны на размещение своих материалов на моем сайте! Вы вносите неоценимый вклад в обучение, воспитание и развитие подрастающего поколения.
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Разница векторов есть 

Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью 
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Период вращения
Период вращения космического объекта — это период времени, которое требуется объекту для совершения полного оборота вокруг своей оси относительно звёзд.
Период вращения (физический термин) — промежуток времени, в течение которого точка совершает полный оборот, двигаясь по окружности.
Периоды вращения некоторых объектов:
| Меркурий | 58,646225199 дней |
| Венера | 243,018483986 дней |
| Марс | 1,03 дней |
| Земля | 0,9972696323 дней |
| Луна | 27,321613297 дней |
| Нептун | 0,671250000 дней |
См. также
Примечания
 |
 Небесная механика Небесная механика | |
|---|---|
| Законы и задачи | Законы Ньютона • Закон всемирного тяготения • Законы Кеплера • Задача двух тел • Задача трёх тел • Гравитационная задача N тел • Задача Бертрана • Уравнение Кеплера |
| Небесная сфера | Система небесных координат: галактическая • горизонтальная • первая экваториальная • вторая экваториальная • эклиптическая • Международная небесная система координат • Сферическая система координат • Ось мира • Небесный экватор • Прямое восхождение • Склонение • Эклиптика • Равноденствие • Солнцестояние • Фундаментальная плоскость |
| Параметры орбит | Кеплеровы элементы орбиты: эксцентриситет • большая полуось • средняя аномалия • долгота восходящего узла • аргумент перицентра • Апоцентр и перицентр • Орбитальная скорость • Узел орбиты • Эпоха |
| Движение небесных тел | Движение Солнца и планет по небесной сфере • Эфемериды Конфигурации планет: противостояние • квадратура • парад планет • Кульминация • Сидерический период • Орбитальный резонанс • Период вращения • Предварение равноденствий • Синодический период • Сближение Затмение: солнечное затмение • лунное затмение • сарос • Метонов цикл • Покрытие • Прохождение • Либрация • Элонгация • Эффект Козаи • Эффект Ярковского • Эффект Джанибекова |
| Астродинамика | |
| Космический полёт | Космическая скорость: первая (круговая) • вторая (параболическая) • третья • четвёртая Формула Циолковского • Гравитационный манёвр • Гомановская траектория • Метод оскулирующих элементов • Приливное ускорение • Изменение наклонения орбиты • Стыковка • Точки Лагранжа • Эффект «Пионера» |
| Орбиты КА | Геостационарная орбита • Гелиоцентрическая орбита • Геосинхронная орбита • Геоцентрическая орбита • Геопереходная орбита • Низкая опорная орбита • Полярная орбита • Тундра-орбита • Солнечно-синхронная орбита • Молния-орбита • Оскулирующая орбита |
Полезное
Смотреть что такое «Период вращения» в других словарях:
Период вращения (астрономия) — Период вращения небесного тела это количество времени, требуемое объекту для совершения полного оборота вокруг своей оси относительно неподвижных звёзд. Совпадает с понятием «звёздные сутки», однако применительно к конкретным астрономическим… … Википедия
период — а, м. période f. <лат. periodus<гр. periodos обход, круговращение, орбита небесного тела. 1. Промежуток времени, в который протекает та или иная часть общего процесса. БАС 1. Бывают в жизни его периоды во время которых выступает он из… … Исторический словарь галлицизмов русского языка
Период — (Period) Промежуток времени, период как этап общественного развития, период в науках Период года, период работы, период регистрации, налоговый период, отчетный период, гарантийный период, ледниковый период Содержание Содержание Раздел 1. в других … Энциклопедия инвестора
Период обращения — Сидерический период обращения (от лат. sidus, звезда; род. падеж sideris) промежуток времени, в течение которого какое либо небесное тело спутник совершает вокруг главного тела полный оборот относительно звёзд. Понятие «cидерический период… … Википедия
период — сущ., м., употр. часто Морфология: (нет) чего? периода, чему? периоду, (вижу) что? период, чем? периодом, о чём? о периоде; мн. что? периоды, (нет) чего? периодов, чему? периодам, (вижу) что? периоды, чем? периодами, о чём? о периодах 1. Периодом … Толковый словарь Дмитриева
ПЕРИОД — (греч. periodos путь кругом). 1) промежуток времени между двумя важными историческими событиями. 2) в астрономии то же, что цикл; в арифметике: число цифр, повторяющихся, в том же порядке, бесчисленное множество раз. 3) особенно развитое сложное… … Словарь иностранных слов русского языка
Период колебаний — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия
Период колебания — Период колебаний наименьший промежуток времени, за который система совершает одно полное колебание (то есть возвращается в то же состояние, в котором она находилась в первоначальный момент, выбранный произвольно). Содержание 1 Периоды простейших … Википедия
Синодический период — обращения (от греч. σύνοδος соединение) промежуток времени между двумя последовательными соединениями Луны или какой нибудь планеты Солнечной системы с Солнцем при наблюдении за ними с Земли. При этом соединения планет с Солнцем… … Википедия
Сидерический период — обращения (от лат. sidus, звезда; род. падеж sideris) промежуток времени, в течение которого какое либо небесное тело спутник совершает вокруг главного тела полный оборот относительно звёзд. Понятие «сидерический период обращения»… … Википедия
Как обозначается период обращения?
Интервал времени, за который тело проходит один полный оборот около центра вращения (оси), называют периодом вращения. Период вращения обозначается буквой T и измеряется в единицах времени — секундах. t — время; n — количество оборотов.
Как определить период обращения?
Период обращения — это время, за которое совершается один оборот. Итак, чтобы найти период обращения, надо время, за которое совершено n оборотов, разделить на число оборотов.
Что называется периодом и частотой обращения?
Как называется период обращения?
Период вращения (физический термин) — промежуток времени, в течение которого точка совершает полный оборот, двигаясь по окружности. Период вращения Земли относительно точки весеннего равноденствия называется звёздными сутками.
Чему равна частота обращения?
Что такое сидерический период обращения?
Сидери́ческий пери́од обраще́ния (от лат. sidus, звезда; род. падеж sideris) — промежуток времени, в течение которого какое-либо небесное тело-спутник совершает вокруг главного тела полный оборот относительно звёзд.
Как определить частоту по периоду?
Период найдем, зная циклическую частоту колебаний: T=2πω0(1.1).
Что измеряется в герцах?
Частота — это количество изменений направления тока за секунду. Для измерения частоты используется международная единица герц (Гц). 1 герц равен 1 колебанию в секунду. Герц (Гц) = 1 герц равен 1 колебанию в секунду.
Что такое период волны?
Период волны — Период волны: время, за которое волна пробегает путь, равный расстоянию между соседними вершинами волнового профиля…
Как называется период обращения планеты вокруг Солнца?
Сидерическим или звездным периодом обращения (Т) планеты называется промежуток времени, в течение которого планета совершает один полный оборот вокруг Солнца по своей орбите.
Какие существуют периоды обращения планет?
Средний сидерический период вращения Солнца 25.4 суток, средний синодический период вращения солнечных пятен, равен 27.2753 суткам.
…
| Планета | Сидерический период |
|---|---|
| Меркурий | 87,97 дней |
| Венера | 224,7 дней |
| Земля | 1 год или 365,2564 дней |
| Луна (вокруг Земли) | 27,322 дней |
Что такое сидерический период обращения Луны и чему он равен?
Сидерический период обращения — промежуток времени, в течение которого какое либо небесное тело спутник совершает вокруг главного тела полный оборот относительно звёзд. Понятие «С. п. о.» применяется к обращающимся вокруг Земли Луне (Сидерический месяц) и искусственным… …
Как определить частоту вращения?
ν=1T(1). Частота, в этом случае — это число полных колебаний (N), совершающихся за единицу времени: ν=NΔt(2), где Δt — время за которое происходят N колебаний.
Какие бывают частоты?
Диапазоны радиочастот и длин радиоволн
| № | Обозн. МСЭ | Диапазон частот |
|---|---|---|
| 5 | LF | 30—300 кГц |
| 6 | MF | 300—3000 кГц |
| 7 | HF | 3—30 МГц |
| 8 | VHF | 30—300 МГц |
Что такое период обращения в каких единицах он измеряется?
Интервал времени, за который тело проходит один полный оборот около центра вращения (оси), называют периодом вращения. Период вращения обозначается буквой T и измеряется в единицах времени — секундах.
Движение по окружности, период обращения и частота.
1. Равномерное движение по окружности
Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.
Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.
Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.
Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке.
Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.
2. Период вращения и вращающаяся частота
Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.
Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.
Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.
При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:
Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: 
Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:
частота вращения равна количеству полных оборотов за одну секунду.
Частота вращения и период обращения связаны следующим соотношением:
Частоту в СИ измеряют в
3. Вращательное движение
В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.
Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.
Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.
ПРОВЕРЬТЕ СЕБЯ
1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.
2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением: 
3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.