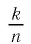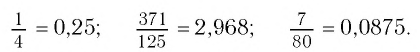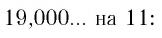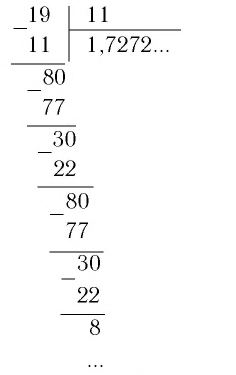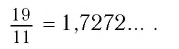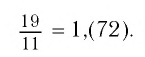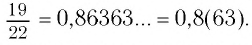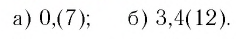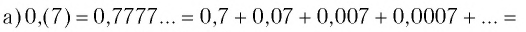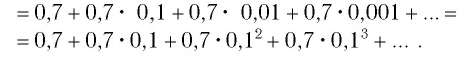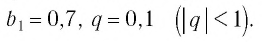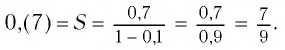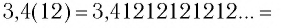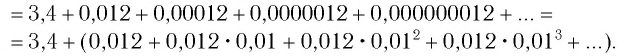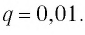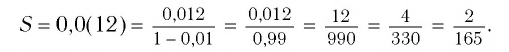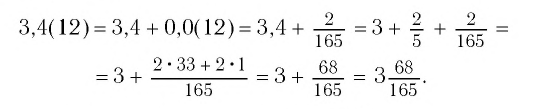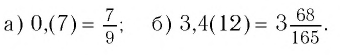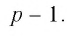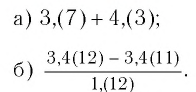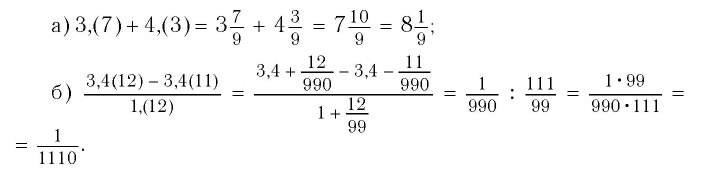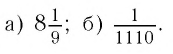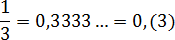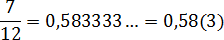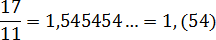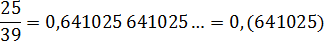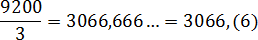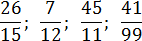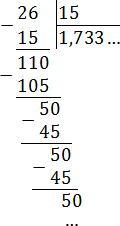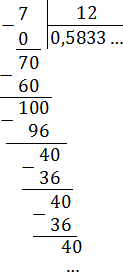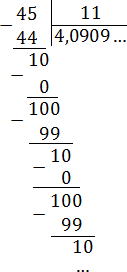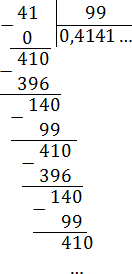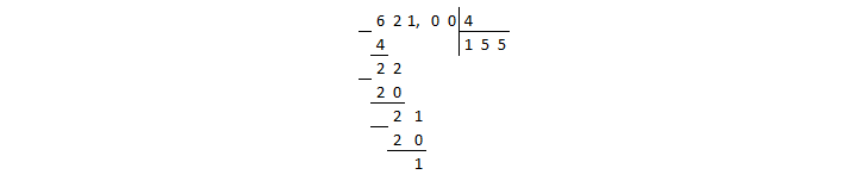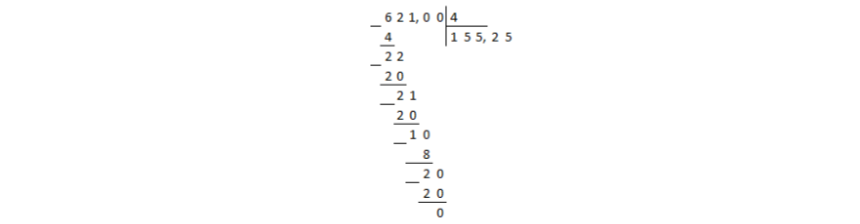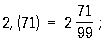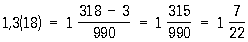Что такое периодическая десятичная дробь

Периодические дроби с примерами решения

Каждое рациональное число является действительным числом, а поэтому может быть записано в виде десятичной дроби — конечной или бесконечной. Хорошо известно, как это делается, когда

Применим теперь этот метод обращения обыкновенной дроби в десятичную к числу 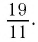Для этого разделим

Таким образом,

Бесконечная дробь, стоящая в правой части этого равенства, содержит периодически повторяющуюся группу цифр 72. Эта группа цифр называется периодом дроби, а сама дробь — периодической. При записи таких дробей период заключают в скобки и пишут один раз:

(Читается: «Одна целая семьдесят два в периоде».)

Еще один пример:

(Читается: «Нуль целых восемь десятых шестьдесят три в периоде».)

Приписывая к конечной десятичной дроби бесконечно много нулей, мы получаем бесконечную десятичную дробь. Поэтому конечные десятичные дроби тоже считаются периодическими с периодом 0. (При делении двух натуральных чисел не могут получиться дроби с числом 9 в периоде, поэтому в школьном курсе алгебры их не рассматривают.)

Приведенные примеры дают возможность догадаться, что каждое рациональное число записывается в виде бесконечной десятичной периодической дроби.

Чтобы в этом убедиться, заметим, что для обращения обыкновенной дроби 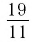в десятичную мы на каждом шаге остаток от деления (он был равен либо 8, либо 3) умножали на 10 и делили на 11. Но при делении на 11 вообще возможны лишь 11 различных остатков. Значит, на каком-то шаге остаток обязательно повторится (в нашем примере это случилось на третьем шаге), и поэтому в результате деления должна получиться периодическая дробь.

Наоборот, каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число.

Каждую периодическую десятичную дробь можно рассматривать либо как сумму бесконечно убывающей геометрической прогрессии, либо как сумму конечной десятичной дроби и сумму бесконечно убывающей геометрической прогрессии. Это позволяет представлять периодические десятичные дроби в виде обыкновенных дробей.

Пример №1

Обратить в обыкновенную дробь число:

Решение:

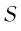
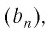
Таким образом, число 0,(7) есть — сумма бесконечно убывающей геометрической прогрессии где

Значит,

б)

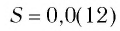
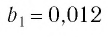
Сумму, стоящую в скобках, обозначим буквой S. Тогда есть сумма бесконечно убывающей геометрической прогрессии с первым членом и знаменателем

Значит,

Ответ:

Изучением периодических дробей занимался великий немецкий математик К- Ф. Гаусс (1777—1855). Уже в детстве он делил единицу на все подряд простые числа р из первой тысячи. При этом Гаусс подметил, что, начиная с какого-то места, десятичные знаки начинают повторяться, т. е. получаются периодические десятичные дроби. А периоды некоторых дробей достигали нескольких сотен десятичных знаков. Рассматривая эти примеры, Гаусс установил, что число цифр в периоде всегда является делителем числа

Пример №2

Найти значение выражения:

Решение:

Обратив каждое из чисел в обыкновенную дробь (см. пример 1), получим:

Ответ:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Периодические десятичные дроби

Помните, как в самом первом уроке про десятичные дроби я говорил, что существуют числовые дроби, не представимые в виде десятичных (см. урок «Десятичные дроби»)? Мы еще учились раскладывать знаменатели дробей на множители, чтобы проверить, нет ли там чисел, отличных от 2 и 5.

Так вот: я наврал. И сегодня мы научимся переводить абсолютно любую числовую дробь в десятичную. Заодно познакомимся с целым классом дробей с бесконечной значащей частью.

— это любая десятичная дробь, у которой:

Поскольку определений много, стоит подробно рассмотреть несколько таких дробей:

Эта дробь встречается в задачах чаще всего. Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6. Для удобства повторяющиеся части отделены друг от друга пробелом — в настоящем решении так делать не обязательно.

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Как видите, определение периодической дроби основано на понятии значащей части числа. Поэтому если вы забыли что это такое, рекомендую повторить — см. урок «Умножение и деление десятичных дробей».

Переход к периодической десятичной дроби

Рассмотрим обыкновенную дробь Разложим ее знаменатель на простые множители. Возможны два варианта:

Чтобы задать периодическую десятичную дробь, надо найти ее периодическую и непериодическую часть. Как? Переведите дробь в неправильную, а затем разделите числитель на знаменатель «уголком».

При этом будет происходить следующее:

Вот и все! Повторяющиеся цифры после десятичной точки обозначаем периодической частью, а то, что стоит спереди — непериодической.

Задача. Переведите обыкновенные дроби в периодические десятичные:

Все дроби без целой части, поэтому просто делим числитель на знаменатель «уголком»:

Как видим, остатки повторяются. Запишем дробь в «правильном» виде:

В итоге получается дробь:

Записываем в нормальном виде:

Переход от периодической десятичной дроби к обыкновенной

Рассмотрим периодическую десятичную дробь Требуется перевести ее в классическую «двухэтажную». Для этого выполним четыре простых шага:

Задача. Приведите к обыкновенной неправильной дроби числа:

Работаем с первой дробью:

В скобках содержится лишь одна цифра, поэтому период Далее умножаем эту дробь Имеем:

Вычитаем исходную дробь и решаем уравнение:

Теперь разберемся со второй дробью. Итак,

Период k = 2, поэтому умножаем все

Снова вычитаем исходную дробь и решаем уравнение:

100 X − X =
99 X = 3207;
X = 3207/99 = 1069/33.

Приступаем к третьей дроби: Схема та же самая, поэтому я просто приведу выкладки:

Период k = 1 ⇒ умножаем все на 10 k = 10 1 = 10;

Наконец, последняя дробь: Опять же, для удобства периодические части отделены друг от друга пробелами. Имеем:

Источник

Периодические десятичные дроби

Вы будете перенаправлены на Автор24

Бесконечные десятичные дроби

Десятичные дроби после запятой могут содержать бесконечное количество цифр.

Бесконечную десятичную дробь практически невозможно записать полностью, поэтому при их записи ограничиваются только некоторым конечным количеством цифр после запятой, после чего ставят многоточие, которое указывает на бесконечно продолжающуюся последовательность цифр.

Периодические десятичные дроби

Готовые работы на аналогичную тему

Бесконечные десятичные периодические дроби представляются рациональными числами. Другими словами, любая периодическая дробь может быть переведена в обыкновенную дробь, а любая обыкновенная дробь может быть представлена в виде периодической дроби.

Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби

Для остальных случаев используется другой способ перевода обыкновенной дроби в десятичную>:

числитель нужно заменить десятичной дробью с любым числом нулей после десятичной запятой;

разделить числитель дроби на знаменатель (деление выполняется как деление натуральных чисел в столбик, а в частном ставят десятичную запятую после окончания деления целой части делимого).

Решение.

Деление дошло до десятичной запятой в делимом, а остаток при этом получили не нулевой. В таком случае в частном ставится десятичная запятая и продолжается деление столбиком, не взирая на запятые:

В остатке получили нуль, значит деление окончено.

Для перевода обыкновенной дроби в десятичную выполним деление в столбик:

Общий вывод о переводе обыкновенных дробей в десятичные:

Источник

Алгебра. 7 класс

Конспект урока

Периодические десятичные дроби. Периодичность десятичного разложения обыкновенной дроби

Перечень рассматриваемых вопросов:

Понятие бесконечной периодической десятичной дроби.

Примеры бесконечной периодической десятичной дроби.

Представление рационального числа в видебесконечной периодической десятичной дроби.

Любое целое число и любую конечную десятичную дробь можно считать бесконечной периодической десятичной дробью или коротко: периодической дробью.

Любое положительное рациональное число

преобразуется в положительную дробь.

Любая периодическая дробь – это десятичное разложение некоторого положительного рационального числа

Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют «чистой».

Если в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют «смешанной».

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

На прошлом уроке мы рассмотрели условия, при которых обыкновенную дробь можно представить в виде конечной десятичной.

А как поступать, когда невозможно представить её в таком виде?

Введём понятие бесконечной периодической десятичной дроби.

Если знаменатель q несократимой дроби p/q не имеет делителей, кроме 2 и 5, то эта дробь преобразуется в конечную десятичную дробь.

Если знаменатель содержит, кроме 2 и 5, другие простые делители, то мы не сможем представить её конечной десятичной дробью.

Знаменатель 9 = 3 3

5/9 не преобразуется в конечную десятичную дробь. Убедимся в этом, выполнив деление уголком.

Разделим числитель 5 на знаменатель 9.

Процесс деления в столбик бесконечный. Приходим к выражению 0,555…,

точки означают, что цифра 5 периодически повторяется бесконечно много раз.

Выражение 0,555… называют бесконечной периодической десятичной дробью или коротко: периодической дробью.

Читают: « ноль целых и пять в периоде».

Цифру (5) называют периодом дроби 0,(5).

Говорят, что число пять девятых представлено в виде периодической дроби ноль целых и пять в периоде.

Выражение 5/9 и 0,(5) являются обозначениями одного и того же числа в виде обыкновенной дроби 5/9 и в виде периодической дроби 0,(5).

Рассмотрим ещё пример.

Дробь четыре пятнадцатых несократимая, и её знаменатель имеет простые делители 3 и 5, поэтому деление не может быть конечным. Проверим.

Делим уголком 4 на 15.

читают: «ноль целых две десятых и шесть в периоде».

В примерах мы увидели разные периодические дроби.

Периодические дроби бывают двух видов: «чистые» и «смешанные».

Если в периодической дроби период начинается сразу после запятой, то такую периодическую дробь называют «чистой».

Видно, что в этих дробях период начинается сразу после запятой.

Если же в периодической дроби период начинается не сразу, а после некоторого количества не повторяющихся цифр, то такую периодическую дробь называют «смешанной».

Если применить правило деления уголком к любой несократимой дроби p/q

Где q – знаменатель, который, кроме 2 и 5 имеет другие простые делители, то получится бесконечная периодическая десятичная дробь, или коротко: периодическая дробь.

Приписывая к конечной десятичной дроби бесконечно много нулей, мы её приводим в бесконечную периодическую десятичную дробь с периодом 0.

45 = 45,0 = 45,000… = 45,(0)

0,673 = 0,673000 = 0,673(0).

Значит, любое целое число и любую конечную десятичную дробь можно считать бесконечной периодической десятичной дробью или коротко: периодической дробью.

Любое положительное рациональное число p/q преобразуется в периодическую дробь.

Верно обратное. Любая периодическая дробь – это десятичное разложение некоторого положительного рационального числа p/q.

Периодичность десятичного разложения обыкновенной дроби

Рассмотрим произвольную положительную несократимую дробь p/q

Покажем, что если разделить числитель дроби на знаменатель уголком, то в частном получится либо конечное, либо бесконечное периодическое её преобразование.

Нам известно, чтобы получить конечное десятичное разложение, знаменатель qне должен иметь простых делителей, кроме 2 и 5

В других случаях может быть только бесконечное десятичное разложение, которое является периодическим. Пусть нужно найти десятичное разложение несократимой дроби 15/13.

Будем делить уголком 15 на 13.

Здесь одной звёздочкой отмечен этап вычислений, когда снесена последняя цифра делимого. Получаемые после этого остатки заключены в прямоугольники. Видно, что остатки, отмеченные двумя, тремя звёздочками, равны между собой. Это показывает, что процесс деления носит периодический характер и приводит к бесконечной периодической десятичной дроби, то есть:

Теперь на примере рассмотрим, как можно, зная бесконечную периодическую десятичную дробь, записать её обыкновенной дробью.

Запишем периодическую дробь 0,(7) в виде обыкновенной.

Для этого обозначим искомую величину х. Тогда справедливо равенство

Умножим это равенство на 10, получим

Вычтем из равенства (2) равенство (1).

Применив к дроби 7/9 деление уголком. Снова получим периодическую дробь 0, (7.)

Разбор заданий тренировочного модуля.

Подберите обыкновенную дробь, равную периодической десятичной 0,(14).

Варианты ответов: 14/99, 14/98 14/90

Обозначим искомую величину х. Тогда справедливо равенство:

Умножим это равенство на 100, получим

Вычтем из равенства (2) равенство (1).

Найдите десятичное разложение обыкновенной дроби 769/4950

Решение: Для решения задачи нужно выполнить деление уголком:

Источник

Периодическая дробь

Полезное

Смотреть что такое «Периодическая дробь» в других словарях:

ПЕРИОДИЧЕСКАЯ ДРОБЬ — бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр (период), напр. 0,373737. чисто периодическая дробь или 0,253737. смешанная периодическая дробь … Большой Энциклопедический словарь

периодическая дробь — дробь, бесконечная дробь Словарь русских синонимов. периодическая дробь сущ., кол во синонимов: 2 • бесконечная дробь (2) • … Словарь синонимов

ПЕРИОДИЧЕСКАЯ ДРОБЬ — десятичная дробь, ряд цифр которой повторяется в одном и том же порядке. Например, 0,135135135… есть п. д., которой период 135 и которая равна простой дроби 135/999 = 5/37. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф … Словарь иностранных слов русского языка

Периодическая дробь — Десятичная дробь дробь со знаменателем 10n, где n натуральное число. Имеет особую форму записи: целая часть в десятичной системе счисления, затем запятая и затем дробная часть в десятичной системе счисления, причём количество цифр дробной части … Википедия

периодическая дробь — бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определённая группа цифр (период); например, 0,373737. чисто периодическая дробь или 0,253737. смешанная периодическая дробь. * * * ПЕРИОДИЧЕСКАЯ… … Энциклопедический словарь

ПЕРИОДИЧЕСКАЯ ДРОБЬ — бесконечная десятичная дробь, в к рой, начиная с нек рого места, периодически повторяется определ. группа цифр (период); напр., 0,373737. чисто П. д. или 0,253737. смешанная П. д … Естествознание. Энциклопедический словарь

дробь — См. часть. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. дробь мелочь, часть; дунст, шарик, шрот, картечь; дробное число Словарь русских синонимов … Словарь синонимов

периодическая десятичная дробь — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN circulating decimalrecurring decimalperioding decimalperiodic decimalperiodical decimal … Справочник технического переводчика

Дробь — Если делится какое нибудь целое число а на другое целое число b, т. е. ищется число x, удовлетворяющее условию bx=а, то могут представиться два случая: или в ряду целых чисел найдется число х, которое этому условию удовлетворит, или же окажется,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Десятичная дробь — дробь, знаменатель которой есть целая степень числа 10. Д. д. пишут без знаменателя, отделяя в числителе справа запятой столько цифр, сколько нулей содержится в знаменателе. Например, В такой записи часть, стоящая слева… … Большая советская энциклопедия

Источник