Что такое периодические процессы в физике
Периодическое движение: вращение и колебание
Пока я смотрел прямо вверх (маятник приходился как раз надо мною), мне почудилось, что он двигается. Минуту спустя впечатление подтвердилось. Ход маятника был короткий и, разумеется, медленный. Несколько мгновений я следил за ним с некоторым страхом, но скорей с любопытством. Наконец, наскуча его унылым качанием, я решил оглядеться.
Э. По. Колодец и маятник
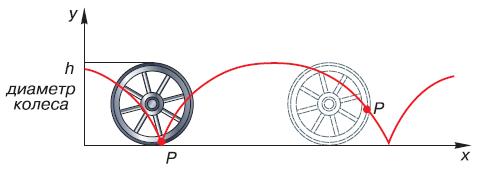
Теперь познакомимся с тем, что происходит, если тело движется прямолинейно и одновременно с этим участвует во вращательном движении. Представьте себе, что катится колесо. Мы уже говорили, что при этом его единственная точка, а именно центр, движется прямолинейно, а остальные, наряду с этим поступательным движением, движутся по окружности вокруг этого центра. Какие траектории будут описывать эти точки, например точка, находящаяся на ободе колеса? Рассмотрим это на графике, где по оси x отложим положение точки относительно места начала её движения, а по оси у – её высоту над землёй (рис. 55). Мы видим, что эта высота меняется в пределах от нуля до размеров диаметра колеса. По мере того как колесо катится всё дальше, высота положения точки на его ободе постепенно повышается, затем начинает плавно снижаться до нуля и снова постепенно повышаться. Такое движение называют периодическим.
Вращение.
Для того чтобы наблюдать периодические движения, необязательно, чтобы тела передвигались в пространстве вдоль прямой линии. В некоторых случаях достаточно, чтобы они просто вращались. В этом легко убедиться, посмотрев на обычные часы. Их стрелки вращаются вокруг оси, и при этом мы замечаем, что они периодически возвращаются в одну и ту же точку циферблата. Можно построить график, аналогичный предыдущему, но теперь по оси x отложить уже не расстояние, а время. По оси у отложим цифры, на которые указывает стрелка. Правда, может возникнуть проблема: как измерять отрезки времени? Этого нельзя сделать по нашим часам, поскольку с их помощью мы измеряем движение стрелок самих часов.
Рис. 55. Траектория движения точки оси и обода колеса при его качении
Для этой цели нужно воспользоваться другими часами, например песочными. Также можно считать свой пульс, как это делал Галилей, или просто довериться внутреннему ощущению времени, о котором мы говорили в предыдущей главе. В любом случае мы знаем, что время проходит, правильнее сказать, длится. И по мере того как оно длится, стрелки на циферблате часов меняют своё положение от 1 до 12, снова от 1 до 12 и так всё время, пока мы будем наблюдать. Но если часы имеют три стрелки – часовую, минутную и секундную, то они будут возвращаться в исходное положение, скажем, к цифре 1, через неодинаковое время. Секундной стрелке для этого понадобится 60 с, минутной – час, т. е. 3600 с, а часовой – 12 ч, т. е. 43 200 с. Это означает, что разные стрелки имеют различные периоды обращения, которые равны соответственно минуте, часу и 12 часам. Такое движение называют периодическим, и мы его уже обсуждали в предыдущем параграфе. По завершении цикла – полного оборота стрелки – она возвращается в исходное положение, и всё начинается сначала. Но это начало будет началом только с точки зрения этой стрелки, а с точки зрения других – процесс будет продолжаться. Если у нас есть часы с разными стрелками, мы можем не пользоваться для отсчёта никакими другими часами, а просто построить график, отложив по оси х показания минутной стрелки, а по оси у – секундной. Ровно через минуту секундная стрелка вернётся в исходное положение и начнёт отсчёт сначала, а минутная сдвинется только на одно деление и будет отсчитывать всё новые отрезки времени. Посмотрев на график, мы увидим, что на нём изображена периодическая функция. Через равные отрезки на оси х, соответствующие минуте, точка будет иметь одинаковые значения, если отсчитывать их по оси х. Мы получили периодическое движение с периодом , составляющим 1 мин.
Под периодическими процессами понимают такие изменения в системах, когда их положение или состояние через определённый промежуток времени возвращается к тому, которое уже имело место раньше. Самым наглядным периодическим процессом служит движение Земли вокруг своей оси и вокруг Солнца. С интервалом в 24 ч Солнце появляется над горизонтом, проходит через зенит и исчезает за другой точкой горизонта. С интервалом приблизительно в 365 дней меняется температура воздуха, распускаются и опадают листья, празднуется день рождения, начинается и кончается учебный год. Но эти примеры хотя и наглядны, но не совсем точны. Солнце сегодня восходит и заходит не совсем в тех точках, где оно это делало вчера, листья в этом году могут распуститься раньше или позже, чем в предыдущем, да и вообще Земля оборачивается вокруг Солнца не за 365 дней, а несколько медленнее. Так что такая периодичность, в отличие от периодичности точных физических процессов, имеет приблизительный характер. Но именно чередование времени суток и времён года послужило для человечества началом измерения времени, создания календаря и внесло порядок в хозяйственное и социальное устройство.
Колебания.
Математический маятник. Процесс колебания математического маятника выглядит следующим образом (рис. 56). Отведём груз на некоторое расстояние. Тогда на него будет действовать сила тяжести, направленная вертикально вниз, и сила натяжения нити. В результате сложения этих сил груз будет совершать движение по дуге. Оказавшись в самой низкой точке, он достигнет положения равновесия. Но он не останавливается, а по инерции продолжает своё движение по дуге, но уже поднимаясь вверх. Так как ускорения во время снижения и во время подъёма равны по модулю, высота этой точки будет в точности равна той, с которой маятник начал своё снижение. Поэтому весь процесс движения повторяется, но в обратном направлении. При отсутствии трения эти колебания будут продолжаться бесконечно.
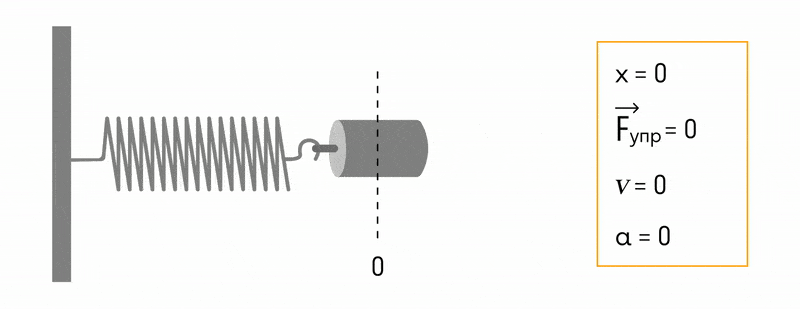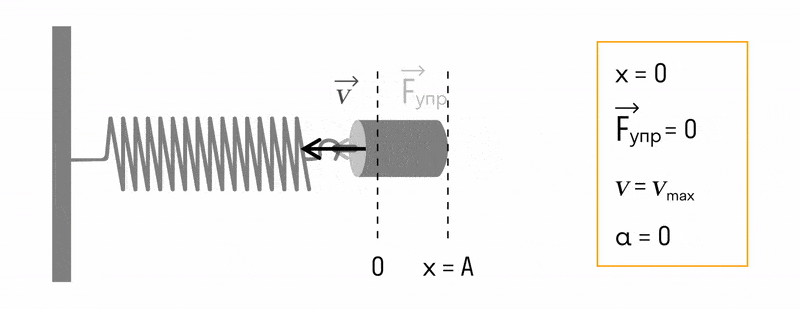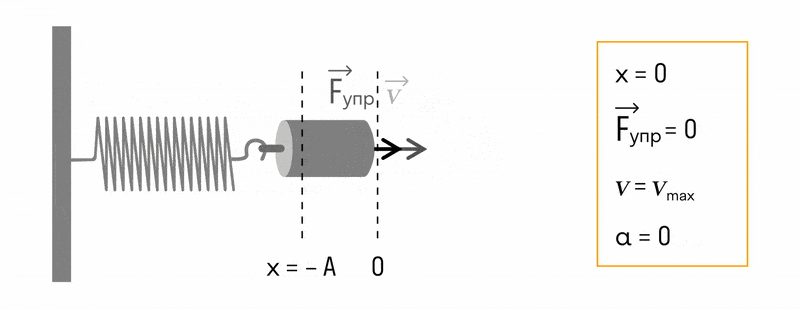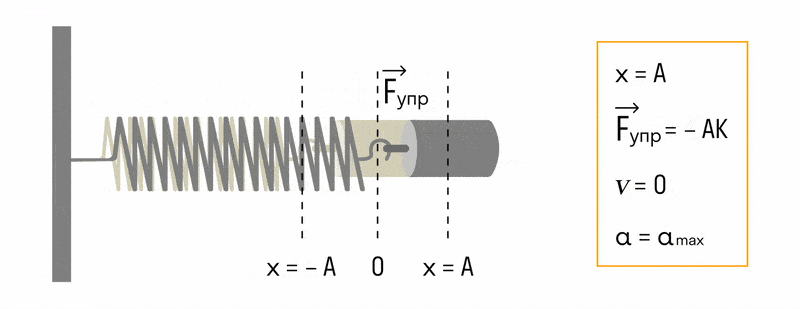
Пружинный маятник. Пружинный маятник похож по принципу действия на математический, но вместо гравитации в нём действует сила упругости пружины. Если закрепить груз на горизонтальной пружине, а затем эту пружину растянуть, то сила упругости будет пропорциональна удлинению пружины (рис. 57). Под действием этой силы груз начнёт двигаться вверх к положению равновесия. Но, дойдя до точки равновесия, он не остановится, а будет по инерции продолжать двигаться в противоположную сторону, сжимая пружину. Упругая сила сжимаемой пружины сначала остановит груз, а потом заставит его двигаться в обратном направлении, пока он не вернётся в исходную точку.
Рис. 56. Разложение сил при колебании маятника
Там на груз опять будет действовать сила растянутой пружины, и колебательный процесс будет продолжаться.
Периодический процесс
Периодичность — это повторяемость явления через определенные промежутки времени. Смену дня и ночи, времён года, фаз Луны мы видим в повседневной жизни. Свет, звук, тепло, радиоволны, переменный электрический ток представляют собой колебательные, периодические процессы. Основой химии является Периодическая система элементов Д. И. Менделеева. Биоритмам посвящены многочисленные монографии и Интернет-проекты (Glass, Хронобиология).
Обнаружены 3—4, 7—11, 20—25, 47—60, 150—300 и 1000-летние периодичности в экономическом развитии общества (Яковец, Анатомия). Описаны волны демократизации и отката от неё в США, российские реформы и контрреформы, начиная с 1801 года и кончая современностью, периодичность во внутренней и внешней политике США (Пантин).
Хорошо известны природные и экологические, демографические, технологические, экономические и социально-политические циклы, периодичности в науке, культуре и образовании (Яковец, Циклические, Атлас, Петухов).
Предложено значительное число математических моделей, описывающих социально-демографические циклы в истории сложных аграрных обществ (с перидичностью порядка 90-100 лет для исламского Ближнего Востока и порядка 150-200 лет для остального мира), т.н. «вековые циклы» (Нефёдов, Турчин, Коротаев, Малков).
Содержание
Терминология и геометрия
Чтобы не делать ошибочных противопоставлений, полезно разобраться в геометрических основах терминов, употребляемых для описания периодичности. Так, циклы (окружности) и волны (синусоиды) являются эквивалентными описаниями, характеризуют одно и то же, просто они даны в разных системах координат. В полярной системе координат независимая переменная (например, время) характеризуется углом и получается окружность, в прямоугольной (Декартовой) системе — независимая переменная задаётся величиной отрезка на горизонтальной оси и получается синусоида (волны одинаковой высоты). Это были описания изменений без развития.
Если имеет место развитие, то окружность превращается в развёртывающуюся спираль, а у синусоиды постоянно увеличивается амплитуда (увеличивается высота волны). Именно эти (эквивалентные) геометрические образы имеются в виду при совремённом употреблении терминов «цикл» и «волна». Принципиальным недостатком обоих отображений является невозможность показать разрывы и скачки (кризисы). Когда они имеют место, становится очевидной необходимость применения функции тангенса или, лучше, дробных функций (см. ниже). Именно такими уравнениями удалось описать Периодический закон Д.И.Менделеева (Имянитов).
Все ранее рассмотренные кривые являются функциями одной переменной и лежат в плоскости. При анализе на качественном уровне часто вместо плоской спирали безосновательно изображается трёхмерная, хотя речь идёт о зависимости от одного или от неопределённого количества параметров.
Составление уравнений
Для описания периодических процессов часто применяются уравнения на основе косинуса (электротехника, радиотехника). Периодическая функция, если она не имеет разрывов, может быть представлена суммой набора разнотипных синусоид (преобразование Фурье). Однако в сложных случаях, в частности, при процессах развития, в соответствии с диалектикой и синергетикой, как правило, происходят разрывы и скачки.
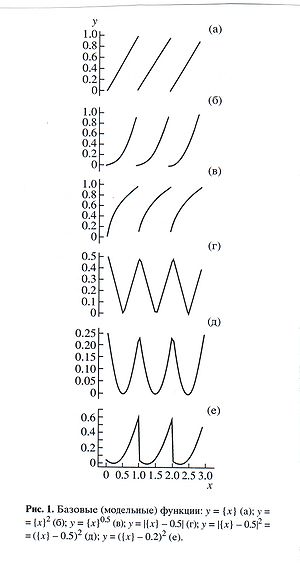
Для описания периодичности особенно полезны дробные функции, которые получаются из любой исходной функции путём отбрасывания целой части от значений зависимого переменного. Так, для простейшего варианта у =
(фигурные скобки означают это отбрасывание),
если x = 0,0 0,1 0,2… 0,5… 1,0 1,1 1,2… 1,5… 2,0 2,1 2,2… 2,5… 3,0, то y = 0,0 0,1 0,2… 0,5… 0,0 0,1 0,2… 0,5… 0,0 0,1 0,2… 0,5… 0,0
Такие функции позволяют с высокой точностью характеризовать самые разные (с разрывами и без них) периодические закономерности. Это достигается благодаря многообразию исходных функций; некоторые примеры приведены на рисунке 1 (Имянитов). Для подбора уравнения годятся обычные компьютерные программы для обработки экспериментальных данных.
Что такое периодические процессы в физике
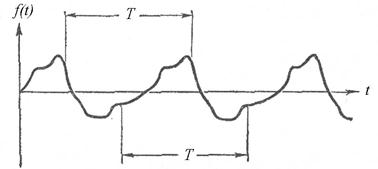
Периодические процессы характеризуются последовательностью состояний, через которые проходит система в течение одного периода. Если эта последовательность точно повторяется через равные промежутки времени, то колебания называются незатухающими. При нарастающих или затухающих колебаниях периодически повторяются только определенные состояния системы, например прохождение колеблющегося тела через положение равновесия и т. п.
Среди множества различных незатухающих колебаний простейшим является гармоническое колебательное движение, описываемое функцией синуса или косинуса:
Во всех случаях, когда рассматривается одно колебание, можно выбрать начало отсчета времени так, чтобы 
однако при одновременном существовании нескольких колебаний (например, при сложении колебаний) начальные фазы каждого колебания отличаются друг от друга и лишь в частных случаях эти фазы могут одновременно равняться нулю.
Формула (4.1) описывает гармонические колебательные движения, происходящие вдоль какой-нибудь линии — отрезка прямой или кривой. В этом случае для определения положения колеблющегося тела достаточно задать только расстояние х от тела до положения равновесия. Колебательные системы, в которых возможно только одно
колебательное движение (вдоль одной линии), изображены на рис. 1.37; их называют колебательными системами с одной степенью свободы. Простой маятник (см. рис. 1.36, а) может совершать два независимых друг от друга колебания в двух взаимно перпендикулярных направлениях, поэтому его относят к колебательным системам, обладающим двумя степенями свободы. Пружинный маятник, изображенный на рис. 1.36, б, может колебаться в трех независимых направлениях и поэтому является колебательной системой с тремя степенями свободы.
Для описания колебательного движения сплошного твердого тела (рис. 1.38, а) удобнее измерять углы поворота а от равновесного состояния; углы, отсчитываёмые по одну сторону от 
, принимаются положительными, по другую сторону — отрицательными. Аналогичное правило знаков выбирается и для тел, совершающих так называемые крутильные колебания (рис. 1.38, б). Гармонические колебания для углов поворота имеют вид 
где 
амплитуда угла поворота.
Гармонические колебания
9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.
Формула периода колебаний
T = t/N
N — количество колебаний [-]
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Формула частоты
ν = N/t = 1/T
N — количество колебаний [-]
Она используется в уравнении гармонических колебаний:
Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
Уравнение гармонических колебаний
x — координата в момент времени t [м]
t — момент времени [с]
2πνtв этом уравнении — это фаза. Ее обозначают греческой буквой φ
Фаза колебаний
t — момент времени [с]
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
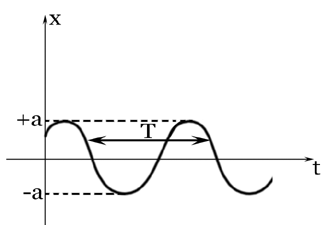
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
Формула периода колебания математического маятника
g — ускорение свободного падения [м/с^2]
На планете Земля g = 9,8 м/с2
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.
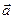(рис. 12.3). Пусть этот вектор первоначально образует с осью x угол a. Теперь приведем этот вектор во вращение с угловой скоростью w вокруг оси, проходящей через точку 0 перпендикулярно плоскости рисунка. Спустя t секунд угол между вектором и осью x вырастет до значения Ф(t) = (wt + a). Проекция вектора a на ось x окажется при этом функцией времени x(t) = aCos(wt+a) и будет совершать гармонические колебания с частотой w.
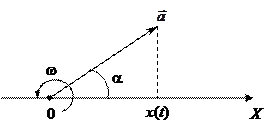Процесс повторится вновь спустя Т секунд. За это время фаза должна увеличиться на 2p радиан.
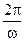. (12.2)
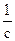= 1 с –1 ] и является величиной, обратной периоду n = 
.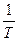