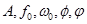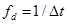Что такое периодический сигнал

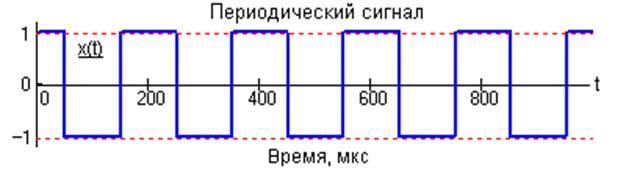
Периодический сигнал

Употребляется в документе:

Сигналы радиотехнические измерительные. Термины и определения

Смотреть что такое «Периодический сигнал» в других словарях:

периодический сигнал — Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени. x(t) = x(t iT), где i любое целое число [ГОСТ 16465 70] Тематики телевидение, радиовещание, видео Обобщающие термины классификация измерительных… … Справочник технического переводчика

Периодический сигнал — 6. Периодический сигнал Детерминированный сигнал, мгновенные значения которого повторяются через равные промежутки времени x(t) = x(t iT), где i любое целое число Источник: ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и… … Словарь-справочник терминов нормативно-технической документации

периодический сигнал — periodinis signalas statusas T sritis automatika atitikmenys: angl. periodic wave vok. periodische Welle, f rus. периодический сигнал, m pranc. onde périodique, f … Automatikos terminų žodynas

сигнал — cигнал 1. Материальный носитель информации, содержащий в себе информацию, кодированную определенным образом. 2. Любая физическая величина (например, температура, давление воздуха, интенсивность света и т. п.), которая изменяется со временем.… … Справочник технического переводчика

гармонический сигнал — ; А амплитуда гармоничного сигнала; w круговая частота; j начальная фаза Примечание Периодический сигнал может быть образован путем периодического повторения импульсов. Соответствующие термины и определения для такого сигнала вводятся так же, как … Справочник технического переводчика

опорный сигнал — Периодический сигнал, с помощью которого осуществляется синхронизация всех основных элементов системы. [Л.М. Невдяев. Телекоммуникационные технологии. Англо русский толковый словарь справочник. Под редакцией Ю.М. Горностаева. Москва, 2002]… … Справочник технического переводчика

ГОСТ 16465-70: Сигналы радиотехнические измерительные. Термины и определения — Терминология ГОСТ 16465 70: Сигналы радиотехнические измерительные. Термины и определения оригинал документа: 40. Абсолютное отклонение сигналов Максимальное значение разности мгновенных значений сигналов, взятых в один и тот же момент времени на … Словарь-справочник терминов нормативно-технической документации

Меандр (радиотехника) — У этого термина существуют и другие значения, см. Меандр (значения). Меандр бесконечный, периодический сигнал прямоугольной формы, широко используемый в радиотехнике. Длительность импульса и длительность паузы в периоде такого сигнала равны … Википедия

Специальная теория относительности — Почтовая марка с формулой E = mc2, посвящённая Альберту Эйнштейну, одному из создателей СТО. Специальная теор … Википедия

Дискретное преобразование Фурье — (в англоязычной литературе DFT, Discrete Fourier Transform) это одно из преобразований Фурье, широко применяемых в алгоритмах цифровой обработки сигналов (его модификации применяются в сжатии звука в MP3, сжатии изображений в JPEG и др.), а … Википедия

Источник

Периодические и непериодические сигналы

Сигнал s(t) называется периодическим, если он точно повторяет свои значения через одинаковые промежутки времени

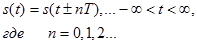При этом наименьший интервал повторения Т называется периодом, частота повторения f0=1/T называется основной частотой.

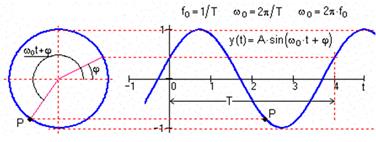
К периодическим сигналам относят гармонические и полигармонические сигналы.

-постоянные величины, которые могут исполнять роль информационных параметров сигнала: А – амплитуда сигнала, f0 –циклическая частота в герцах, ωо – угловая частота в радианах,

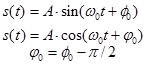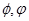
— начальные фазовые углы в радианах.

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов, и описывается суммой гармонических колебаний:

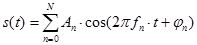
Полиграфические сигналы представляют собой сумму определенной постоянной составляющей (fо=0) и произвольного числа гармонических составляющих с произвольными значениями амплитуд An и фаз jn, с частотами, кратными фундаментальной частоте fp.

Периодический сигнал любой произвольной формы может быть представлен в виде суммы гармонических колебаний с частотами, кратным фундаментальной частоте колебаний fр = 1/Тр.

Непериодический сигнал – почти периодические сигналы близки по своей форме к полигармоническим. Они также представляют собой сумму двух и более гармонических сигналов, с произвольными частотами, отношение которых (хотя бы двух частот минимум ) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик.

Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени.

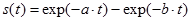
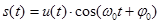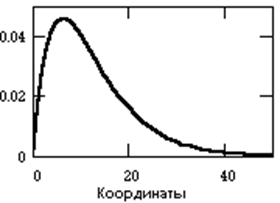
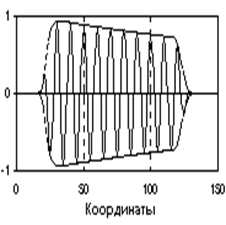
Случайным сигналом называют функцию времени, значения которой заранее неизвестны, и могут быть предсказаны лишь с некоторой вероятностью. Случайный сигнал отображает случайное физическое явление или физический процесс, причем, зарегистрированный в единичном наблюдении, сигнал не воспроизводится при повторных наблюдениях.

В качестве основных статистических характеристик случайных сигналов принимают:

а) закон распределения вероятности нахождения величины сигнала в определенном интервале значений;

б) спектральное распределение мощности сигнала.

Случайные сигналы подразделяют на стационарные и нестационарные. Стационарные сигналы сохраняют свои статистические характеристики в последовательных реализациях случайного процесса.

Отдельную категорию сигналов составляют шумы (noise) и помехи – сигналы, искажающие интересующий сигнал.

Строго говоря, они не являются сигналами в исходном определении, т.к. не несут никакой полезной информации. Но в то же время, часто их называют сигналами в том смысле, что они имеют зависимость от той же независимой переменной, что и основной сигнал, и также порождаются физическими процессами.

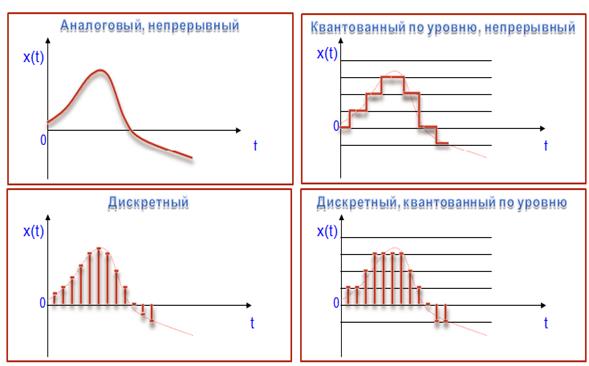
Классы детерминированных сигналов:

— произвольные по величине и непрерывные по времени (аналоговые);

— произвольные по величине и дискретные по времени (дискретные);

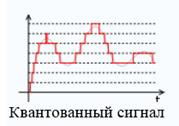
— квантованные по величине и непрерывные по времени (квантованные);

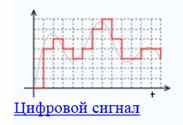
— квантованные по величине и дискретные по времени (цифровые).

Любой сигнал определенные возможные значения на определенном пространстве значений независимой переменной. Как значения, так и независимая переменная могут быть либо непрерывными, либо дискретными.

Непрерывность — свойство, заключающееся в постепенном, плавном, без скачков изменении значений какой-либо переменной, функции или другого математического объекта.

Дискретность — свойство, противопоставляемое непрерывности, прерывность.

Аналоговый (непрерывный) сигнал – сигнал, значения и независимая переменная которого являются непрерывными множествами возможных значений.

Дискретный сигнал – сигнал, независимая переменная которого определена на дискретном множестве, а значения являются непрерывными.

Аналоговый сигнал является непрерывной функцией времени, т.е. однозначно определяется для всех t. Электрический аналоговый сигнал возникает тогда, когда физический сигнал (например, речь) некоторым устройством преобразовывается в электрический.

Цифровой сигнал—сигнал данных, у которого каждый из представляющих параметров описывается функцией дискретного времени и конечным множеством возможных значений.

Соответственно, можно определить следующие преобразования сигналов:

Дискретизация — процесс преобразования аналогового сигнала в дискретный.

Квантование — преобразование аналогового сигнала в квантованный.

Оцифровка — преобразование аналогового сигнала в цифровой.

Восстановление — преобразование сигнала из дискретного или цифрового в аналоговый.

Частота дискретизации дискретного сигнала — частота следования отсчетов.

Период дискретизации — расстояние между двумя соседними отсчетами.

Квантование (quantization) — в информатике разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов.

Квантование по уровню — представление величины отсчѐтов цифровыми сигналами.

Для квантования в двоичном коде диапазон напряжения сигнала от Umin до Umax делится на 2n интервалов.

Величина получившегося интервала (шага квантования):

Сигнал, к которому применены дискретизация и квантование, называется цифровым.

Порядок выполнения лабораторной работы:

Создаем м-файл в среде MatLab: File>New>M-File

Источник

Основы цифровой обработки сигналов

Сигнал это изменение физической величины во времени или пространстве. К примеру, это может быть изменение одномерного сигнала в зависимости от времени. Если мы рассматриваем цифровое изображение это может быть изменение яркости пикселей в зависимости от его положения в пространстве.

Но с точки зрения математики сигнал это функция одной или нескольких независимых переменных. В нашем случае независимыми переменными являются время и положение в пространстве, а зависимыми переменными могут быть значения нашего сигнала x от t или яркости пикселей на цифровом изображении.

Непрерывные и дискретные сигналы:

Непрерывный аналоговый сигнал определен на всем промежутке времени, то есть мы в любой момент времени t можем узнать значение сигнала x. Если мы возьмем эти значения с периодом дискретизации T, то мы получаем дискретный сигнал, значение которого определены только в конкретные моменты времени.

Дискретный сигнал теперь записываем как x[n], и n это номера отчетов дискретной последовательности. Если взглянуть на процесс дискретизации с точки зрения математики, то выходная дискретная последовательность с x[n] формируется, когда мы подставляем в нашу функцию x(t) значение времени t равный nT, где n — это номер дискретного отчета, а T — это период дискретизации.

Периодические сигналы

Периодический сигнал это сигнал, форма которого повторяется во времени. Повторяться во времени может, как форма непрерывных сигналов, так и форма дискретных сигналов. Периодом сигнала называем интервал повторения.

К примеру, у дискретного сигнала y[n] форма повторяется каждые 4, 8, 12 и так далее отчетов, для непрерывного сигнала z[t] форма повторяется каждые 2, 4, 6 и так далее секунд.

Фундаментальным или основным периодом сигналом называется наименьший интервал повторения, то есть для нашего дискретного сигнала y[n] это 4 отчета, а для нашего непрерывно сигнала это две секунды.

Фундаментальная частота

От понятие фундаментального периода мы можем перейти к понятию фундаментальной частоты. Фундаментальная или основная частота также именуемая первая гармоника, это количество основных периода сигнала, приходящихся на единицу времени. Частота измеряется в Герцах, то есть в количестве периодов приходящейся на одну секунду, и фактически является обратной величиной основного периода.

Если мы рассмотрим наш непрерывный сигнал z[t] его основной период равен двум секундам, а это значит, что на одну секунду приходится ровно половина его периода.

Основная частота дискретного сигнала

Но если с непрерывным сигналом все более менее понятно, то есть можем взглянуть на него на временной оси, оценить величины основного периода и подсчитать значение основной частоты, то с дискретным сигналом все не так просто.

Нам доступны значение отчетов, мы знаем их номера в последовательности, но мы не знаем, как они соотносятся с его фундаментальной частотой, и как они соотносятся с частотой дискретизации. Давайте в этом попробуем разобраться на примере.

Возьмем дискретный сигнал, который мы используем для описания в предыдущих статьях. Он имеет период в 4 отчета, где два первых отчета в периоде имеют большую амплитуду, а два последних отчета имеют малую амплитуду.

Нашей задачи в данном примере будет при помощи такого сигнала услышать ноту ля первой октавы, то есть частоту 440 Гц. Для того чтобы это сделать нам обязательно надо понять, как основная частота соотносится с частотой дискретизации сигнала.

Для этого давайте перенесем наш сигнал на временную ось. Основной период данного сигнала высчитывается также, как для непрерывного сигнала, то есть это обратная величина его фундаментальной частоты, в нашем случае единицы делить на 440. Но мы также видим то, что период дискретизации нашего сигнала, обозначим здесь его как ∆t в 4 раза меньше, чем основной период, так как на основной период приходится ровно 4 отсчета.

Выразим частоту дискретизации через период дискретизации, частоту дискретизации можно записать, как единицу делить на ∆t, что получить равно 4 делить на T₀, то есть в нашем случае частота дискретизации должна быть в 4 раза больше, чем наша фундаментальная частота ноты ля первой октавы.

Изменение частоты дискретизации

Если мы рассмотрим наши манипуляции над дискретным сигналом, как манипуляции на аналоговом сигнале, а после этого дискретизацию аналогового сигнала, то вот к чему мы приходим. Когда мы увеличиваем частоту дискретизации, то мы фактически берем дискретные отчеты более быстрого аналогового сигнала, или кладем отчеты того же дискретного сигнала на другую временную сетку.

К примеру, наш дискретный сигнал с периодом дискретизации ∆t можно представить как оцифрованные значения аналогового сигнала с периодом Т₀,

Если теперь те же самые отчеты сигнала, мы положим на более плотную временную сетку с меньшим периодом ∆t, это фактически то же самое как если мы оцифровали более быстрый аналоговый сигнал с меньшим периодом Т₀.

В качестве эталонного, аналогового сигнала мы представили синусоиду, а почему мы так часто используем синусоиду, когда говорим о цифровой обработки сигналов об этом в следующей статье.

Источник

Связь между временной и частотной областями представления сигналов

Электрические сигналы можно исследовать во временной области с помощью осциллографа и в частотной области с помощью анализатора спектра (рисунок 1).

Рисунок 1 – Сигналы, исследуемые во временной и частотной областях

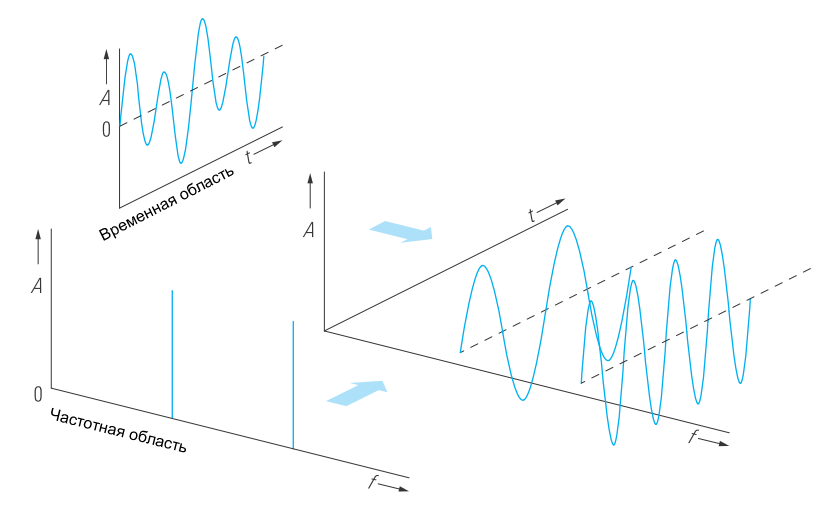
Эти два режима отображения сигналов связаны друг с другом преобразованием Фурье (обозначается как F), поэтому каждый сигнал во временной области имеет характерный частотный спектр. Таким образом, связь представлениями во временной и частотной областях будет следующей:

Чтобы проиллюстрировать эту взаимосвязь, сначала исследуем сигналы только с периодическим откликом во временной области.

Периодические сигналы

Согласно теореме Фурье любой сигнал, являющийся периодическим во временной области, может быть получен из суммы синусоидальных и косинусоидальных сигналов разной частоты и амплитуды. Такая сумма называется рядом Фурье. В этом случае применима следующая формула:

\[x(t) = \frac <2>+ \sum_^ <\infty>A_n \cdot \sin(n \cdot \omega_0 \cdot t) + \sum_^ <\infty>B_n \cdot \cos(n \cdot \omega_0 \cdot t) \qquad (3)\]

Коэффициенты Фурье A₀, A_n и B_n зависят от формы сигнала x(t) и могут быть рассчитаны следующим образом:

\[A_0 = \frac<2> \int_<0>^ x(t) \ dt \qquad (4)\]

\[A_n = \frac<2> \int_<0>^ x(t) \cdot \sin(n \cdot \omega_0 \cdot t) \ dt \qquad (5)\]

\[B_n = \frac<2> \int_<0>^ x(t) \cdot \cos(n \cdot \omega_0 \cdot t) \ dt \qquad (6)\]

На рисунке 2b показан прямоугольный сигнал, аппроксимированный в ряд Фурье. Отдельные компоненты этого ряда Фурье показаны на рисунке 2a. Чем больше этих компонентов, тем итоговый сигнал ближе к идеальным прямоугольным импульсам.

Рисунок 2 – Аппроксимация прямоугольного сигнала путем суммирования различных синусоидальных колебаний

В случае синусоидальных или косинусоидальных сигналов для уравнения 1 можно найти решение в замкнутой форме, и для отображения комплексного спектра будут получены следующие соотношения:

где \(\delta (f-f_0)\) – функция Дирака:

\[\begin \delta (f-f_0) = \begin \infty &\text <если >f-f_0=0 \ \text <, т.е. >f=f_0 \\\ 0 \end \end \\ \int_<-\infty>^ <+\infty>\delta (f-f_0) \ df = 1\]

Можно видеть, что частотный спектр и синусоидального, и косинусоидального сигналов является функцией Дирака при f₀ (смотрите рисунок 4a). Преобразования Фурье синусоидального и косинусоидального сигналов идентичны по величине, так что эти два сигнала демонстрируют идентичный амплитудный спектр на одной и той же частоте f₀.

Чтобы вычислить частотный спектр периодического сигнала, временная характеристика которого описывается рядом Фурье в соответствии с уравнением 3, необходимо преобразовать каждый компонент ряда. Каждый из этих элементов приводит к функции Дирака, то есть дискретной составляющей в частотной области. Поэтому периодические сигналы всегда демонстрируют дискретные спектры, которые также называются линейчатыми спектрами. Например, спектр, показанный на рисунке 3, получен для аппроксимированного прямоугольного сигнала на рисунке 2.

Рисунок 3 – Амплитудный спектр аппроксимированного прямоугольного сигнала, показанного на рисунке 2

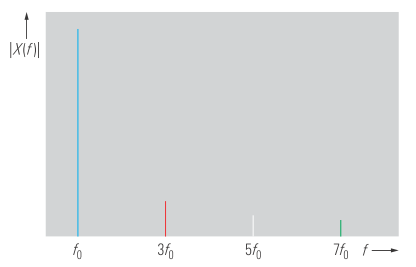
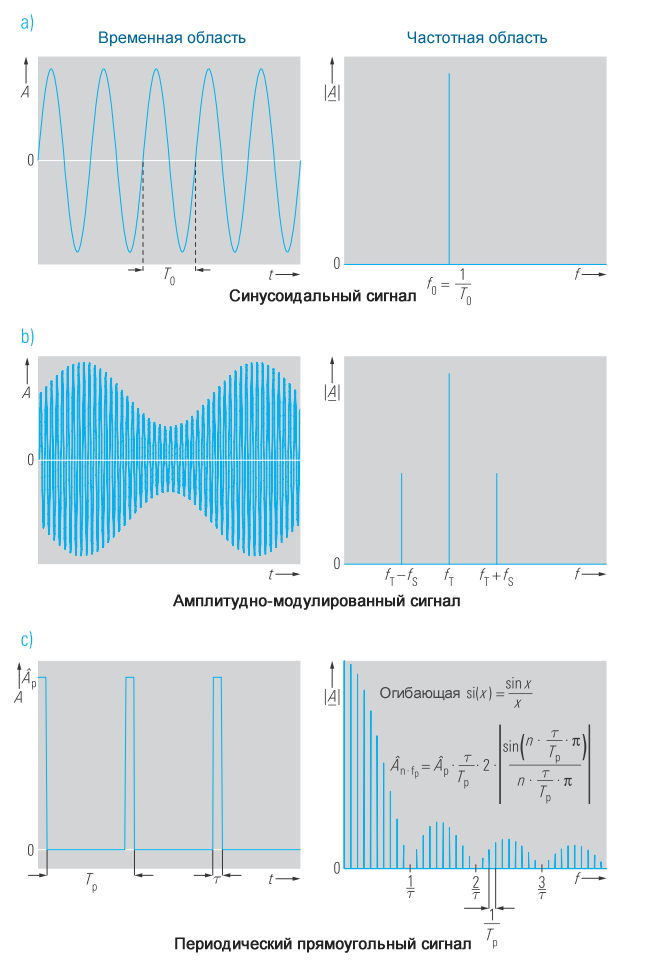
На рисунке 4 показаны еще несколько примеров периодических сигналов во временной и частотной областях.

Рисунок 4 – Периодические сигналы во временной и частотной области (амплитудные спектры)

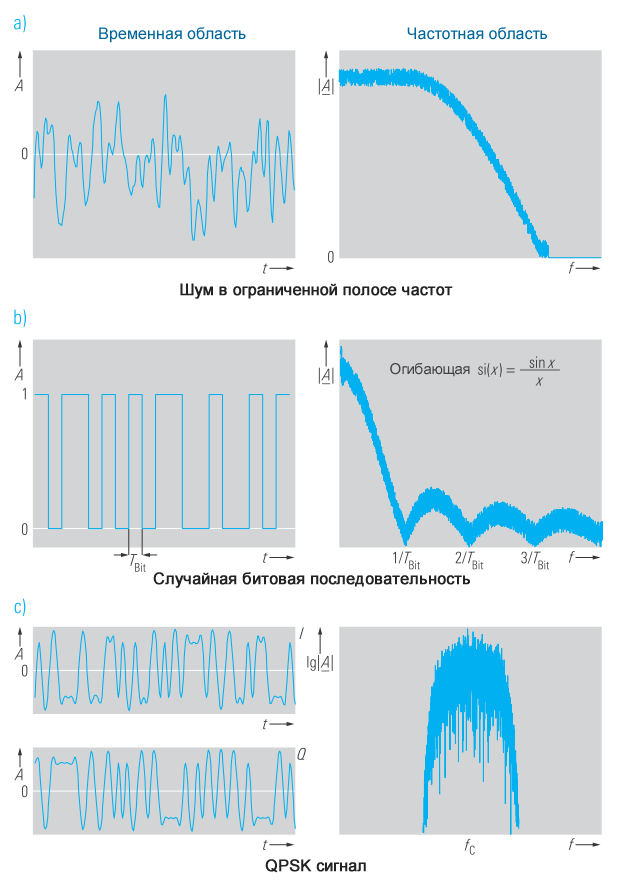
Непериодические сигналы

Сигналы с непериодическим поведением во временной области не могут быть описаны рядом Фурье. Следовательно, частотный спектр таких сигналов не может быть составлен из дискретных спектральных составляющих. Непериодические сигналы демонстрируют непрерывный частотный спектр с частотно-зависимой спектральной плотностью. Представление такого сигнала в частотной области вычисляется с помощью преобразования Фурье (уравнение 1).

Подобно синусоидальным и косинусоидальным сигналам, решение уравнения 1 в замкнутой форме может быть найдено для многих сигналов. Таблицы с такими парами преобразований можно найти в [1].

Для сигналов со случайными характеристиками во временной области, таких как шум или случайные битовые последовательности, решение в замкнутой форме встречается редко. В этом случае частотный спектр легче определить численным решением уравнения 1.

На рисунке 5 показаны некоторые непериодические сигналы во временной и частотной областях.

Рисунок 5 – Непериодические сигналы во временной и частотной областях

В зависимости от типа выполняемого измерения, полезными могут быть исследования либо во временной, либо в частотной области. Например, для измерения джиттера сигнала цифровой передачи данных требуется осциллограф. Для определения содержания гармоник более полезно исследовать сигнал в частотной области.

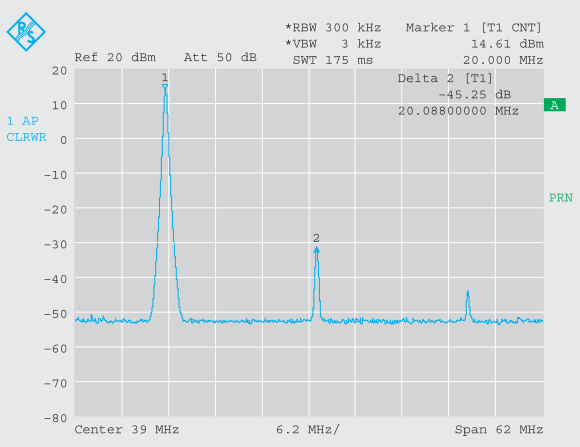
Сигнал, показанный на рисунке 6, кажется чистой синусоидой с частотой 20 МГц. Исходя из приведенных выше соображений, можно было бы ожидать, что его частотный спектр будет состоять только из одного компонента на частоте 20 МГц.

Рисунок 6 – Синусоидальный сигнал (f = 20 МГц), исследуемый на осциллографе

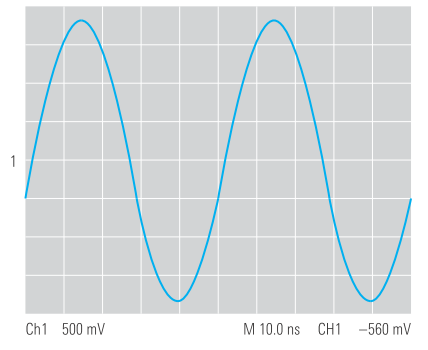
Однако при исследовании сигнала в частотной области с помощью анализатора спектра становится очевидным, что основная гармоника (гармоника 1-го порядка) накладывается на несколько гармоник более высокого порядка, то есть кратные 20 МГц (рисунок 7). Исследуя сигнал во временной области, эту информацию получить нелегко, и практическая количественная оценка высших гармоник невозможна. Кратковременную стабильность частоты и амплитуды синусоидального сигнала намного легче исследовать в частотной области, чем во временной (смотрите также раздел 6.1 «Измерение фазового шума).

Рисунок 7 – Исследование синусоидального сигнала, показанного на рисунке 6, в частотной области с помощью анализатора спектра

Источник