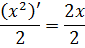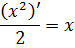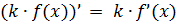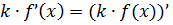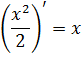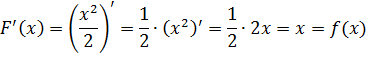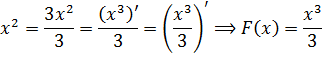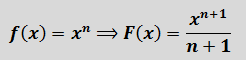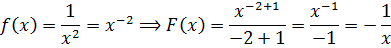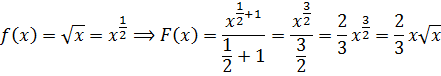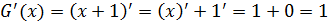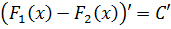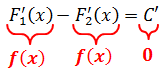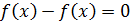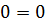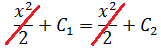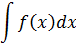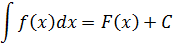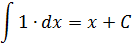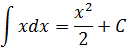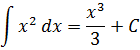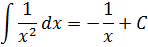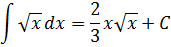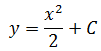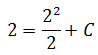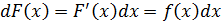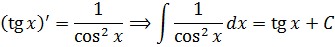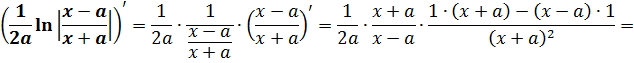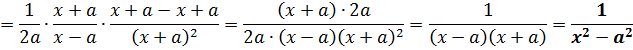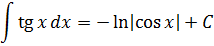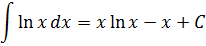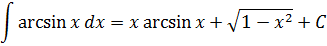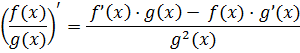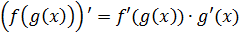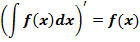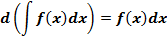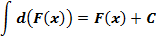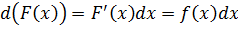Что такое первообразная функции простыми словами

Что такое первообразная? Понятие первообразной.

Прежде чем знакомиться с понятием первообразной, давайте в самых общих чертах вспомним самую обычную производную. Не углубляясь в занудную теорию пределов, приращений аргумента и прочего, можно сказать, что нахождение производной (или дифференцирование) — это просто математическая операция над функцией. И всё. Берётся любая функция (допустим, f(x) = x 2 ) и по определённым правилам преобразовывается, превращаясь в новую функцию. И вот эта самая новая функция и называется производной.

Грубо говоря, f(x) = x 2 — это мама, а f’(x) = 2x — её любимая дочка.) Это понятно. Идём дальше.

Математики — народ неугомонный. На каждое своё действие стремятся найти противодействие. 🙂 Есть сложение — есть и вычитание. Есть умножение — есть и деление. Возведение в степень — извлечение корня. Синус — арксинус. Точно также есть дифференцирование – значит, есть и… интегрирование.)

А теперь поставим такую интересную задачу. Есть у нас, допустим, такая простенькая функция f(x) = 1. И нам надо ответить на такой вопрос:

Производная КАКОЙ функции даёт нам функцию f(x) = 1?

Иными словами, видя дочку, с помощью анализа ДНК, вычислить, кто же её мамаша. 🙂 Так от какой же исходной функции (назовём её F(x)) произошла наша производная функция f(x) = 1? Или, в математической форме, для какой функции F(x) выполняется равенство:

Пример элементарный. Я старался.) Просто подбираем функцию F(x) так, чтобы равенство сработало. 🙂 Ну как, подобрали? Да, конечно! F(x) = x. Потому, что:

Разумеется, найденную мамочку F(x) = x надо как-то назвать, да.) Знакомьтесь!

Первообразной для функции f(x) называется такая функция F(x), производная которой равна f(x), т.е. для которой справедливо равенство F’(x) = f(x).

Вот и всё. Больше никаких научных хитростей. В строгом определении добавляется ещё дополнительная фраза «на промежутке Х». Но мы пока в эти тонкости углубляться не будем, ибо наша первоочередная задача — научиться находить эти самые первообразные.

В нашем случае как раз и получается, что функция F(x) = x является первообразной для функции f(x) = 1.

Почему? Потому что F’(x) = f(x) = 1. Производная икса есть единица. Возражений нет.)

Термин «первообразная» по-обывательски означает «родоначальница», «родитель», «предок». Сразу же вспоминаем самого родного и близкого человека.) А сам поиск первообразной — это восстановление исходной функции по известной её производной. Иными словами, это действие, обратное дифференцированию. И всё! Сам же этот увлекательный процесс тоже называется вполне научно — интегрирование. Но об интегралах — позже. Терпение, друзья!)

Запоминаем:

Интегрирование — это математическая операция над функцией (как и дифференцирование).

Интегрирование — операция, обратная дифференцированию.

Первообразная — результат интегрирования.

А теперь усложним задачу. Найдём теперь первообразную для функции f(x) = x. То есть, найдём такую функцию F(x), чтобы её производная равнялась бы иксу:

Кто дружит с производными, тому, возможно, на ум придёт что-то типа:

Что ж, респект и уважуха тем, кто помнит таблицу производных!) Верно. Но есть одна проблемка. Наша исходная функция f(x) = x, а (x 2 )’ = 2x. Два икс. А у нас после дифференцирования должен получиться просто икс. Не катит. Но…

Мы с вами народ учёный. Аттестаты получили.) И со школы знаем, что обе части любого равенства можно умножать и делить на одно и то же число (кроме нуля, разумеется)! Так уж тождественные преобразования устроены. Вот и реализуем эту возможность себе во благо.)

Мы ведь хотим, чтобы справа остался чистый икс, верно? А двойка мешает… Вот и берём соотношение для производной (x 2 )’ = 2x и делим обе его части на эту самую двойку:

Так, уже кое-чего проясняется. Идём дальше. Мы знаем, что любую константу можно вынести за знак производной. Вот так:

Все формулы в математике работают как слева направо, так и наоборот — справа налево. Это значит, что, с тем же успехом, любую константу можно и внести под знак производной:

В нашем случае спрячем двойку в знаменателе (или, что то же самое, коэффициент 1/2) под знак производной:

А теперь внимательно присмотримся к нашей записи. Что мы видим? Мы видим равенство, гласящее, что производная от чего-то (это что-то — в скобочках) равняется иксу.

Полученное равенство как раз и означает, что искомой первообразной для функции f(x) = x служит функция F(x) = x 2 /2. Та, что стоит в скобочках под штрихом. Прямо по смыслу первообразной.) Что ж, проверим результат. Найдём производную:

Отлично! Получена исходная функция f(x) = x. От чего плясали, к тому и вернулись. Это значит, что наша первообразная найдена верно.)

Полученная формулка, между прочим, справедлива не только для натурального показателя степени n, но и для любого другого — отрицательного, дробного. Это позволяет легко находить первообразные от простеньких дробей и корней.

Что такое неопределённый интеграл? Таблица интегралов.

Идём дальше. Те студенты, которые хотя бы мало-мальски «шарят» в производных, — люди грамотные. И, возможно, уже приготовили мне убойный вопрос. 🙂

Скажем, чему равна производная для функции F(x) = x? Ну, единица, единица — слышу недовольные ответы… Всё верно. Единица. Но… Для функции G(x) = x+1 производная тоже будет равна единице:

Также производная будет равна единице и для функции x+1234, и для функции x-10, и для любой другой функции вида x+C, где С — любая константа. Ибо производная любой константы равна нулю, а от прибавления/вычитания нуля никому ни холодно ни жарко.)

Получается неоднозначность. Выходит, что для функции f(x) = 1 первообразной служит не только функция F(x) = x, но и функция F₁(x) = x+1234 и функция F₂(x) = x-10 и так далее!

Но! Всех наших родственников-первообразных объединяет одно важное свойство. На то они и родственники.) Свойство настолько важное, что в процессе разбора приёмов интегрирования мы про него ещё не раз вспомним. И будем вспоминать ещё долго.)

Вот оно, это свойство:

Любые две первообразные F₁(x) и F₂(x) от одной и той же функции f(x) отличаются на константу:

Кому интересно доказательство — штудируйте литературу или конспекты лекций.) Ладно, так уж и быть, докажу. Благо доказательство тут элементарное, в одно действие. Берём равенство

и дифференцируем обе его части. То есть, просто тупо ставим штрихи:

Вот и всё. Как говорится, ЧТД. 🙂

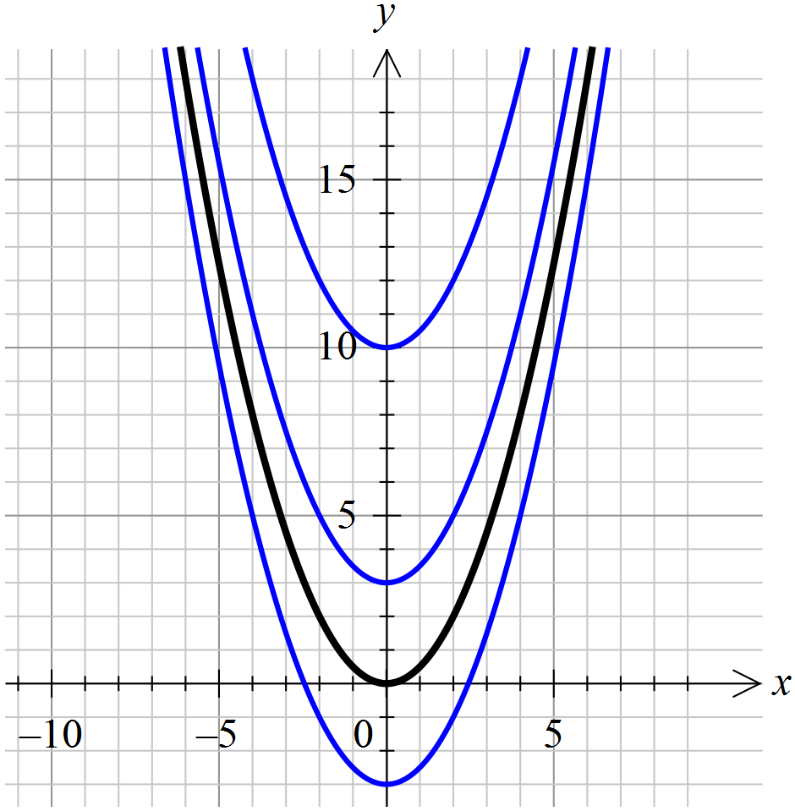
Посмотрим, как это выглядит на примере функции f(x) = x. Все её первообразные, как нам уже известно, имеют общий вид F(x) = x 2 /2+C. На картинке это выглядит как бесконечное множество парабол, получаемых из «основной» параболы y = x 2 /2 сдвигом вдоль оси OY вверх или вниз в зависимости от значения константы С.

Помните школьное построение графика функции y=f(x)+a сдвигом графика y=f(x) на «а» единиц вдоль оси игреков?) Вот и тут то же самое.)

Причём, обратите внимание: наши параболы нигде не пересекаются! Оно и естественно. Ведь две различные функции y₁(x) и y₂(x) неизбежно будут соответствовать двум различным значениям константы — С₁ и С₂.

Поэтому уравнение y₁(x) = y₂(x) никогда не имеет решений:

А теперь мы плавненько подходим ко второму краеугольному понятию интегрального исчисления. Как мы только что установили, у всякой функции f(x) существует бесконечное множество первообразных F(x) + C, отличающихся друг от друга на константу. Это самое бесконечное множество тоже имеет своё специальное название.) Что ж, прошу любить и жаловать!

Что такое неопределённый интеграл?

Множество всех первообразных для функции f(x) называется неопределённым интегралом от функции f(x).

Вот и всё определение.)

«Интеграл» — с подробной расшифровкой этого зверского слова мы познакомимся в следующем большом разделе, посвящённом определённым интегралам. А пока, в грубой форме, будем считать интегралом нечто общее, единое, целое. А интегрированием — объединение, обобщение, в данном случае переход от частного (производной) к общему (первообразным). Вот, как-то так.

Обозначается неопределённый интеграл вот так:

Читается так же, как и пишется: интеграл эф от икс дэ икс. Или интеграл от эф от икс дэ икс. Ну, вы поняли.)

Теперь разберёмся с обозначениями.

∫ — значок интеграла. Смысл тот же, что и штрих для производной.)

d — значок дифференциала. Не пугаемся! Зачем он там нужен — чуть ниже.

f(x) — подынтегральная функция (через «ы»).

f(x)dx — подынтегральное выражение. Или, грубо говоря, «начинка» интеграла.

Согласно смыслу неопределённого интеграла,

Здесь F(x) — та самая первообразная для функции f(x), которую мы так или иначе нашли сами. Как именно нашли — не суть. Например, мы установили, что F(x) = x 2 /2 для f(x)=x.

А теперь вернёмся к нашим самым первым примерам на поиск первообразной. В терминах неопределённого интеграла можно теперь смело записать:

И так далее.) Идея понятна, думаю. Ни в коем случае не забываем приплюсовывать константу С!

Что такое интегральная константа и зачем она нужна?

Вопрос очень интересный. И очень (ОЧЕНЬ!) важный. Интегральная константа из всего бесконечного множества первообразных выделяет ту линию, которая проходит через заданную точку.

В чём суть. Из исходного бесконечного множества первообразных (т.е. неопределённого интеграла) надо выделить ту кривую, которая будет проходить через заданную точку. С какими-то конкретными координатами. Такое задание всегда и везде встречается при начальном знакомстве с интегралами. Как в школе, так и в ВУЗЕ.

Среди множества всех первообразных функции f=x выделить ту, которая проходит через точку (2;2).

Начинаем думать головой… Множество всех первоообразных — это значит, сначала надо проинтегрировать нашу исходную функцию. То есть, икс (х). Этим мы занимались чуть выше и получили такой ответ:

А теперь разбираемся, что именно мы получили. Мы получили не одну функцию, а целое семейство функций. Каких именно? Вида y=x 2 /2+C. Зависящее от значения константы С. И вот это значение константы нам и предстоит теперь «отловить».) Ну что, займёмся ловлей?)

Удочка наша — семейство кривых (парабол) y=x 2 /2+C.

Константы — это рыбины. Много-много. Но на каждую найдётся свой крючок и приманка.)

А что же служит приманкой? Правильно! Наша точка (-2;2).

Вот и подставляем координаты нашей точки в общий вид первообразных! Получим:

Отсюда уже легко ищется C = 0.

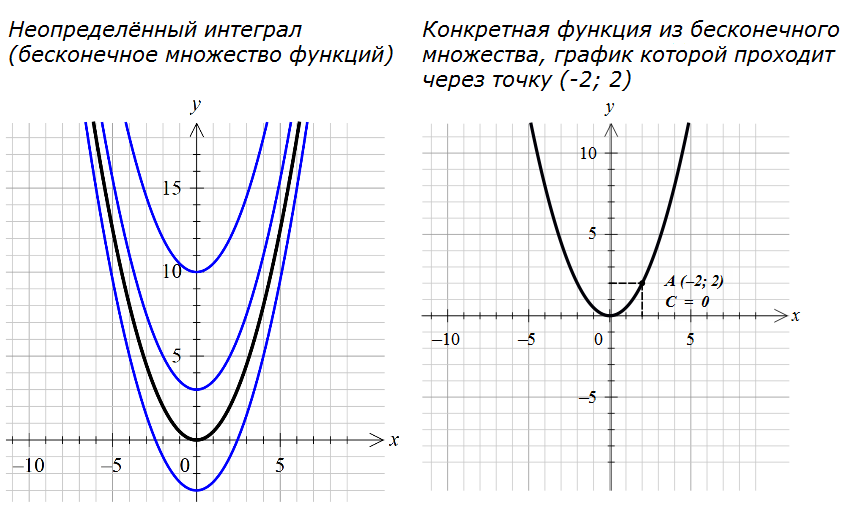
Что сиё означает? Это значит, что из всего бесконечного множества парабол вида y=x 2 /2+C только парабола с константой С=0 нам подходит! А именно: y=x 2 /2. И только она. Только эта парабола будет проходить через нужную нам точку (-2; 2). А в се остальные параболы из нашего семейства проходить через эту точку уже не будут. Через какие-то другие точки плоскости — да, а вот через точку (2; 2) — уже нет. Уловили?

Для наглядности вот вам две картинки — всё семейство парабол (т.е. неопределённый интеграл) и какая-то конкретная парабола, соответствующая конкретному значению константы и проходящая через конкретную точку:

Видите, насколько важно учитывать константу С при интегрировании! Так что не пренебрегаем этой буковкой «С» и не забываем приписывать к окончательному ответу.

А теперь разберёмся, зачем же внутри интегралов везде тусуется символ dx. Забывают про него студенты частенько… А это, между прочим, тоже ошибка! И довольно грубая. Всё дело в том, что интегрирование — операция, обратная дифференцированию. А что именно является результатом дифференцирования? Производная? Верно, но не совсем. Дифференциал!

В нашем случае, для функции f(x) дифференциал её первообразной F(x), будет:

Кому непонятна данная цепочка — срочно повторить определение и смысл дифференциала и то, как именно он раскрывается! Иначе в интегралах будете тормозить нещадно….

Поэтому, строго говоря, интеграл «берётся» не от функции f(x), как принято считать, а от дифференциала f(x)dx! Но, в упрощённом варианте, принято говорить, что «интеграл берётся от функции». Или: «Интегрируется функция f(x)«. Это одно и то же. И мы будем говорить точно так же. Но про значок dx при этом забывать не будем! 🙂

И сейчас я подскажу, как его не забыть при записи. Представьте себе сначала, что вы вычисляете обычную производную по переменной икс. Как вы обычно её пишете?

Вот так: f’(x), y’(x), у’_x. Или более солидно, через отношение дифференциалов: dy/dx. Все эти записи нам показывают, что производная берётся именно по иксу. А не по «игреку», «тэ» или какой-то там другой переменной.)

Так же и в интегралах. Запись ∫ f(x)dx нам тоже как бы показывает, что интегрирование проводится именно по переменной икс. Конечно, это всё очень упрощённо и грубо, но зато понятно, я надеюсь. И шансы забыть приписать вездесущее dx резко снижаются.)

Итак, что такое же неопределённый интеграл — разобрались. Прекрасно.) Теперь хорошо бы научиться эти самые неопределённые интегралы вычислять. Или, попросту говоря, «брать». 🙂 И вот тут студентов поджидает две новости — хорошая и не очень. Пока начнём с хорошей.)

Новость хорошая. Для интегралов, так же как и для производных, существует своя табличка. И все интегралы, которые нам будут встречаться по пути, даже самые страшные и навороченные, мы по определённым правилам будем так или иначе сводить к этим самым табличным.)

Итак, вот она, таблица интегралов!

Вот такая вот красивая табличка интегралов от самых-самых популярных функций. Рекомендую обратить отдельное внимание на группу формул 1-2 (константа и степенная функция). Это — самые употребительные формулы в интегралах!

Третья группа формул (тригонометрия), как можно догадаться, получена простым обращением соответствующих формул для производных.

C четвёртой группой формул (показательная функция) — всё аналогично.

А вот четыре последние группы формул (5-8) для нас новые. Откуда же они взялись и за какие такие заслуги именно эти экзотические функции, вдруг, вошли в таблицу основных интегралов? Чем же эти группы функций так выделяются на фоне остальных функций?

Так уж сложилось исторически в процессе развития методов интегрирования. Когда мы будем тренироваться брать самые-самые разнообразные интегралы, то вы поймёте, что интегралы от перечисленных в таблице функций встречаются очень и очень часто. Настолько часто, что математики отнесли их к табличным.) Через них выражаются очень многие другие интегралы, от более сложных конструкций.

Ради интереса можно взять какую-нибудь из этих жутких формул и продифференцировать. 🙂 Например, самую зверскую 7-ю формулу.

Всё нормально. Не обманули математики. 🙂

Ответ. Ничем не хуже.) Просто вышеназванные интегралы (от тангенса, логарифма, арксинуса и т.д.) не являются табличными. И встречаются на практике значительно реже, нежели те, что представлены в таблице. Поэтому знать наизусть, чему они равны, вовсе не обязательно. Достаточно лишь знать, как они вычисляются.)

Что, кому-то всё-таки невтерпёж? Так уж и быть, специально для вас!

Ну как, будете заучивать? 🙂 Не будете? И не надо.) Но не волнуйтесь, все подобные интегралы мы обязательно найдём. В соответствующих уроках. 🙂

Что ж, теперь переходим к свойствам неопределённого интеграла. Да-да, ничего не поделать! Вводится новое понятие — тут же и какие-то его свойства рассматриваются.

Свойства неопределённого интеграла.

Теперь не очень хорошая новость.

В отличие от дифференцирования, общих стандартных правил интегрирования, справедливых на все случаи жизни, в математике нету. Это фантастика!

Например, вы все прекрасно знаете (надеюсь!), что любое произведение любых двух функций f(x)·g(x) дифференцируется вот так:

Любое частное дифференцируется вот так:

А любая сложная функция, какой бы накрученной она ни была, дифференцируется вот так:

И какие бы функции ни скрывались под буквами f и g, общие правила всё равно сработают и производная, так или иначе, будет найдена.

А вот с интегралами такой номер уже не пройдёт: для произведения, частного (дроби), а также сложной функции общих формул интегрирования не существует! Нету никаких стандартных правил! Вернее, они есть. Это я зря математику обидел.) Но, во-первых, их гораздо меньше, чем общих правил для дифференцирования. А во-вторых, большинство методов интегрирования, о которых мы будем разговаривать в следующих уроках, очень и очень специфические. И справедливы лишь для определённого, очень ограниченного класса функций. Скажем, только для дробно-рациональных функций. Или каких-то ещё.

А какие-то интегралы, хоть и существуют в природе, но вообще никак не выражаются через элементарные «школьные» функции! Да-да, и таких интегралов полно! 🙂

Именно поэтому интегрирование — гораздо более трудоёмкое и кропотливое занятие, чем дифференцирование. Но в этом есть и своя изюминка. Занятие это творческое и очень увлекательное.) И, если вы хорошо усвоите таблицу интегралов и освоите хотя бы два базовых приёма, о которых мы поговорим далее ( замена переменной и интегрирование по частям ), то интегрирование вам очень понравится. 🙂

А теперь познакомимся, собственно, со свойствами неопределённого интеграла. Их всего ничего. Вот они.

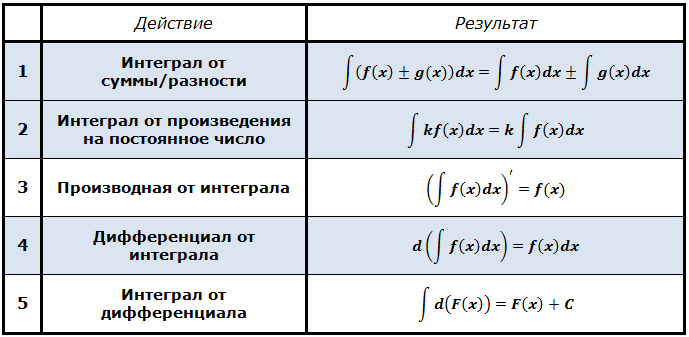
Первые два свойства полностью аналогичны таким же свойствам для производных и называются свойствами линейности неопределённого интеграла. Тут всё просто и логично: интеграл от суммы/разности равен сумме/разности интегралов, а постоянный множитель можно вынести за знак интеграла.

А вот следующие три свойства для нас принципиально новые. Разберём их поподробнее. Звучат по-русски они следующим образом.

Третье свойство

Производная от интеграла равна подынтегральной функции

Конечно же, в ответе могут получаться настолько зверские и громоздкие функции, что и обратно дифференцировать их неохота, да. Но лучше, по возможности, стараться себя проверять. Хотя бы в тех примерах, где это несложно.)

Идём дальше, по порядочку.

Четвёртое свойство

Тут ничего особенного. Суть та же самая, только dx на конце появляется. Согласно предыдущему свойству и правилам раскрытия дифференциала.

Пятое свойство

Тоже очень простое свойство. Им мы тоже будем регулярно пользоваться в процессе решения интегралов. Особенно — в методе подведения функции под знак дифференциала и замены переменной .

Вот такие вот полезные свойства. Занудствовать с их строгими доказательствами я здесь не собираюсь. Желающим предлагаю это сделать самостоятельно. Прямо по смыслу производной и дифференциала. Докажу лишь последнее, пятое свойство, ибо оно менее очевидно.

Итак, у нас есть утверждение:

Вытаскиваем «начинку» нашего интеграла и раскрываем, согласно определению дифференциала:

На всякий случай, напоминаю, что, согласно нашим обозначениям производной и первообразной, F’(x) = f(x).

Вставляем теперь наш результат обратно внутрь интеграла:

Получено в точности определение неопределённого интеграла (да простит меня русский язык)! 🙂

Что ж. На этом наше начальное знакомство с таинственным миром интегралов считаю состоявшимся. На сегодня предлагаю закруглиться. Мы уже достаточно вооружены, чтобы идти в разведку. Если не пулемётом, то хотя бы водяным пистолетом базовыми свойствами и таблицей. 🙂 В следующем уроке нас уже ждут простейшие безобидные примеры интегралов на прямое применение таблицы и выписанных свойств.

Источник