Что такое первый десяток в математике
Числа от 1 до 100. Состав числа. Круглые числа
Числа от 1 до 100
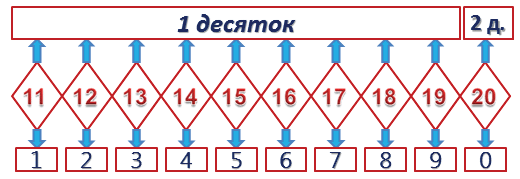
Предыдущее и последующее число
56 , 57
56, 57
Однозначные и двузначные числа
Вспомни, что каждая цифра в записи занимает определенное место.
Единицы стоят на первом месте справа.
Десятки стоят на втором месте справа.
Однозначные числа записываются ОДНОЙ цифрой: 5, 9, 2, 5.
Двузначные числа записываются ДВУМЯ цифрами: 54, 91, 42, 85.
Состав двузначного числа
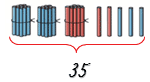
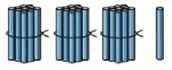
Всего на рисунке 35 палочкек.
35 = 30 + 5
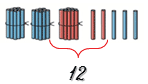
Красных палочек 12.
12 = 10 + 2
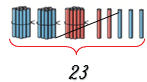
Синих палочек всего 23.
23 = 2 дес. 3 ед.
23 = 20 + 3
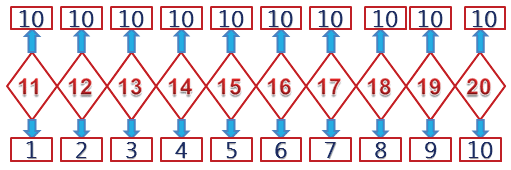
Теперь научимся представлять числа в виде суммы разрядных слагаемых.
Какие разряды выделяют в двузначных числах?
В двузначных числах выделяют разряд десятков и разряд единиц, то есть двузначное число можно представить следующим образом:
В числе 35 три десятка и 9 единиц:
Сравнение двузначных чисел
| Число | 42 | 24 |
| Количество десятков | 4 | 2 |
| Количество единиц | 2 | 4 |
1. Сравнение двузначных чисел всегда начинается с десятков.
2. Если количество десятков одинаково, тогда переходят к сравнению единиц.
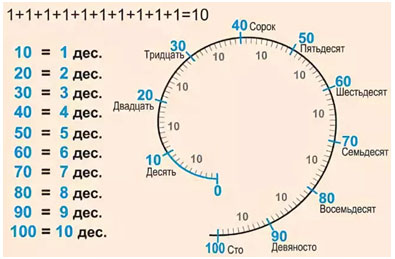
Круглые числа
10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
1 дес. + 4 дес. = 5 дес.
10 + 40 = 50
Счёт десятками
Десять любых предметов можно назвать – ОДИН ДЕСЯТОК.
Десятками можно считать:
Действия с десятками и единицами
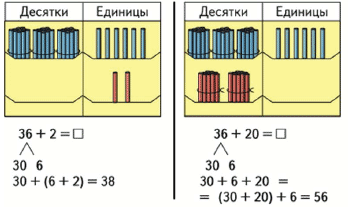
Как решить пример 34 + 25?
3 дес. и 4 ед. + 2 дес. и 5 ед. = 5 дес. 9 ед.
Можно записать короче:
Число 34 представляю в виде суммы разрядных слагаемых: 30 и 4, число 25 тоже представляю как 20 и 5. Теперь начинаю вычислять:
Сначала складываю единицы:
Теперь складываю десятки:
Запись решения выглядит так:
34 + 25 = (30 + 20) + (4 + 5) = 50 + 9 = 59
Десятки складываются с десятками.
Единицы складываются с единицами.
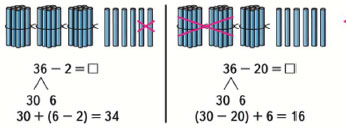
Можно рассуждать так:
Число 38 представим в виде суммы разрядных слагаемых 30 и 8, а число 16 представим так: 10 и 6. Удобно число 6 вычесть из числа 8, получим 2. Затем число 10 вычтем из числа 30, получим 20. Теперь 2 прибавим к числу 20. Получим 22.
Десятки вычитаются из десятков.
Единицы вычитаются из единиц.
Мы рассмотрели случаи устных вычислений с двузначными числами.
Познакомиться с письменными приема вычислений (сложением в столбик и вычитанием в столбик) можно в нашем справочнике.
Поделись с друзьями в социальных сетях:
ПОНЯТИЕ ЧИСЛА И ЧИСЛА ПЕРВОГО ДЕСЯТКА
Целые неотрицательные числа называют натуральными в связи с тем, что они были придуманы человечеством для счета элементов реальных множеств, а также для обозначения результатов процесса измерения величин.
Таким образом, различают число как результат счета элементов множества и число как результат измерения величин (длина, масса, время и т.д.)
Альтернативные программы по математике для начальных классов различаются главным образом способом знакомства ребенка с этими характеристиками числа.
Как и многие математические понятия, понятие натурального числа возникло из потребностей практики.
Простейшим способом сравнения множеств было установление взаимно – однозначного соответствия между множествами, т.е. образование пар элементов из обоих множеств. Если такое соответствие имело место, то множества считались равночисленными (все пары – полные).
Если взаимно – однозначное соответствие устанавливалось между элементами одного множества и только частью элементов второго множества (некоторые элементы второго множества оставались без пары), то считали, что в первом множестве меньше элементов, чем во втором.
 |  |  |  |  |  |
Например: Чего больше, кружков или квадратов?
При этом хорошо видно, что считать пары нет надобности, оставшиеся без пары («лишние») фигуры покажут, каких было больше (и на сколько больше).
Наука, изучающая числа и действия с ними получила название «арифметика» ( от греческого arithmos – число).
Натуральные числа обозначают при счете реальные предметы. Само по себе число не зависит от характера и свойства предметов множества, т.е. одно и тоже число может символизировать количество объектов какого угодно характера.
Каждая группа ( множество) может быть охарактеризовано только одним числом ( и если при повторном пересчете объектов получается другой результат, это означает ошибку счета).
Цифра – это символ, обозначающий число на письме. Число мы называем и слышим. Цифру мы видим, пишем и называем.
Римские цифры употребляются только в печатном изображении, арабские цифры – в печатном (1,2,3,4,5,6,7,8,9) и курсивном (прописном) изображение (1,2,3,4,5,6,7,8,9).
В любой из упомянутых систем обозначения чисел больше, чем цифр.
Натуральные или целые положительные числа 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,… записанные в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.
Количественное и порядковое числа взаимосвязаны, при пересчете элементы конечного множества не только расставляются в определенном порядке, но и устанавливается также, сколько элементов содержит множество (последний порядковый номер, называемый при счете, является характеристикой количества элементов множества).
Например: последнее яблоко – пятое, значит их всего пять. Эти две роли натурального числа нашли отражение в русском языке: порядковые натуральные числа выражаются порядковыми числительными (первый, второй, третий и т.д.), количественные – количественными числительными (один, два и т.д.)
Процесс счета подчиняется определенным правилам:
1) первому отмеченному предмету ставится в соответствие число 1 (наименьшее натуральное число);
2) на каждом следующем шаге отмечается (нумеруется) предмет, еще не отмеченный ранее (нельзя считать один и тот же предмет дважды);
3) ему ставится в соответствие число, следующее за последним из уже названных (натуральные числа расположены в строгом равномерном порядке).
Данные правила определяют принцип образования чисел в натуральном ряду: каждое следующее число на единицу больше предыдущего.
Усвоение ребенком этого принципа является центральной задачей изучения нумерации первого десятка в школе.
Следствием этого принципа является идея (бесконечности ряда натуральных чисел (как бы ни было велико число, всегда можно найти следующее, добавив к нему единицу), а также способ нахождения значений выражений вида 5+1; 8+1; 6-1; 7-1 и т.п. путем называния либо следующего, либо предыдущего числа. Иными словами, для нахождения значения данных выражений нет необходимости выполнять какой-то прием арифметических действий, достаточно понимать, что добавление 1 ведет к получению следующего по счету числа, а убавление 1 – означает возврат к предыдущему по счету числу. Именно для получения результатов в таких выражениях ребенок заучивал наизусть названия чисел в прямом и обратном порядке.
В умение считать входят: знание слов-числительных, знание («запомненность») порядка их называния при счете, понимание смысла процесса нумерации элементов множества, понимание того, что последний названный номер является характеристикой количественного состава множества, и умение соблюдать правила счета. Для того чтобы ребенок не осваивал процесс счета на формальном уровне, на первых порах этот процесс следует обязательно сопровождать предметными действиями: откладыванием, показыванием, а также проговариванием вслух.
Следует помнить, что можно предлагать ребенку посчитать двойками, десятками и т.п., но нельзя говорить: «Посчитай от 10 обратно». Процесс счета «векторный», т.е. возможен по определению только в сторону увеличения номеров. Перечисление названий чисел в обратном порядке не является счетом, поскольку слово-числительное, названное при счете последним, является ответом на вопрос «Сколько?», т.е. характеризует количество предметов данной совокупности.
Умение называть числительные в обратном порядке является базовым для обучения ребенка процессу отсчитывания, поэтому формировать такое умение необходимо, но формулировать задание следует в виде: «Назови числа в обратном порядке». (Но не «посчитай»!) Таким же образом формулируются задания: «Назови числа от 6 до 9» и т.п. (Но не «посчитай от 6 до 9».)
Место числа в ряду определено способом его получения: каждое следующее число становится в ряду справа от предыдущего. Для понимания такого порядка расположения ребенок должен предварительно освоиться с процессом перевода пространственного расположения объектов, подчиненных отношению «следовать за», в плоскость, где отношение «следовать за» подразумевает «ближайшее справа», а «следовать пере» (предшествовать) – ближайшее слева.
Число предыдущее – стоит в ряду чисел левее данного. При счете оно называется непосредственно перед данным, количественно содержит на одну единицу меньше данного.
Число последующее (следующее) – стоит в ряду чисел правее данного. При счете оно называется непосредственно после данного, количественно содержит на одну единицу больше данного.
Так, число пять является предыдущим к числе шесть; число семь является последующим числа шесть. В первом классе числа пять и семь по отношению к числу шесть часто называют соседями.
Так, соседями числа восемь являются числа семь и девять. Хорошее понимание принципа построения натурального ряда чисел ведет в дальнейшем к легкому освоению приемов присчитывания и отсчитывания по 1 и легкому выполнению вычислений в случаях:
7+1 17+1 177+1 10 277+1
Во всех случаях ссылка на принцип построения натуральной последовательности чисел является наиболее рациональной вплоть до 4 класса (общий пример вычислений):
¾ Прибавляя к числу 1, получаем следующее по счету;
¾ Вычитая из числа 1, получаем предыдущее по счету.
Этот же прием является действующим и в трудных случаях:
9+1 19+1 199+1 999+1 99 999+1
При нахождении ответа в данных примерах удобно ссылаться на порядок счета: следующим за числом 99 999 является число 100 000; предшествующим числом для числа 1000 является 999.
Термин «состав однозначных чисел» подразумевает обучение ребенка умению представлять данную количественную совокупность в виде составных частей, обозначая их количественные характеристики словом ( числом) или любыми другими символами (числовыми фигурами):
Состав числа на числовых фигурах:
   |   |  |      |
  |   |
Пять – это три и два Пять – это четыре и один Пять это два и три
Не следует торопиться вводить цифровую символику при изучении состава числа:
 |
   1 1 |
    4 4 |
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Разряды и классы чисел
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Число 10. Образование числа 10
Ты любишь цирк? Уверена, что да! На сегодняшнем уроке я приглашаю тебя на цирковое представление. Посмотри, кто там будет выступать.
Давай всех посчитаем:
Итак, всего девять артистов. Но здесь кого-то не хватает!
Конечно же, в цирке не обойтись без фокусника!
Ты можешь сказать, сколько сейчас артистов в цирке?
Их было девять и теперь добавился еще один. Помнишь, мы учили, что если к числу прибавить еще один, то получается последующее число? У числа девять последующим числом является число десять.
Давай еще раз пересчитаем всех артистов:
Теперь у нас всего десять артистов.
Правило образования числа десять следующее: к девяти добавить один.
Потренируйся считать в пределах десяти. Посмотри на следующую картинку. Здесь мячики, шляпы и палочки для жонглирования. Определи, каких предметов десять. Чтобы не путаться при счете, обращай внимание на цвет предметов.
А сейчас нам нужно вспомнить порядковый счет в пределах десяти:
Теперь самостоятельно определи количество предметов, которые фокусник достал из шляпы, а затем пересчитай их по порядку.
Скажи, что он достал пятым? А что восьмым?
Запись числа 10
Пришло время познакомиться с формой записи числа десять. Его нужно писать так:
Ты заметил, что запись числа десять отличается от всех других чисел, которые мы выучили раньше? Что в ней особенного?
Верно, это число записывается не одной, а двумя цифрами сразу. Ты ведь угадал цифру 1 и цифру 0. Но в числе 10 их надо писать вместе.
Запись числа 10 похожа на атрибуты нашего фокусника. Его пустая шляпа напоминает нам число и цифру 0. А волшебную палочку можно сравнить с цифрой 1.
Поскольку для записи числа 10 мы используем две цифры, то это число называют двузначным.
Числа, с которыми мы познакомились раньше, записываются с использованием одной цифры. Поэтому их принято называтьоднозначными. Это 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Число 10 – это первое и наименьшее двузначное число.
В тетради число 10 надо писать так:
Цифры 1 и 0 нужно писать рядом в двух соседних клетках. Обрати внимание, что при записи числа 10, цифру 0 следует писать в левой части клетки, начиная от середины верхней границы клетки.
Вспомни, как мы учились писать эти цифры и самостоятельно потренируйся записывать число 10.
Запомни! 10 – это число, а записывается оно цифрами 1 и 0.
Состав числа 10
Главное умение, необходимое фокуснику – это ловкость рук. Руками он может двигать предметы, не прикасаясь к ним, доставать предметы из воздуха и многое другое.
Сколько пальцев на обеих руках фокусника? Правильно 10.
Как ты узнал, что у него 10 пальцев?
Верно, у тебя их тоже 10. Сейчас мы на пальцах выучим состав числа 10.
Положи руки перед собой. Пересчитай, сколько пальцев на одной руке. А потом на второй. Что у тебя получилось?
Правильно, пять пальцев на одной руке и пять пальцев на второй.
Значит 10 – это 5 и 5.
Теперь рассмотрим другие комбинации. Посчитай только большие пальцы.
Их 2. А сколько остальных пальцев? Правильно, 8.
Значит, 10 – это 2 и 8.
А теперь посчитай все пальцы левой руки и большой палец правой руки вместе.
Получилось 6. Сколько осталось пальцев на правой руке? Точно, 4.
Значит, 10 – это 6 и 4.
А теперь покажи знак «ок» и посчитай, сколько пальцев торчат вверх, а сколько зажаты.
Значит, 10 – это 3 и 7.
Все отлично. Мы рассмотрели все комбинации!
Обязательно не забудем о том, что 9 и 1 тоже 10. Мы это выучили, когда познакомились с порядком образования числа 10.
Давай теперь все еще раз повторим и обобщим.
9 и 1 или 1 и 9
8 и 2 или 2 и 8
7 и 3 или 3 и 7
6 и 4 или 4 и 6
5 и 5
Чтобы получше запомнить состав числа 10, выполни задание. На этой картинке найди все пары чисел, которые являются составляющими числа 10.
Почаще вспоминай состав числа 10, пересчитывая пальцы на руках. Тебе эти знания очень пригодятся в дальнейшем при решении сложных примеров.
Последовательность чисел в пределах 10
Итак, мы выучили числа от 0 до 10. Их называют натуральными числами. Каждое число указывает количество элементов в определенном множестве.
Посмотри на картинки и определи, с каким множеством соотносится каждое число.
Посмотри, вот числа, которые мы выучили.
7 3 5 2 4 1 0 9 6 10 8
Ты все числа вспомнил? Давай проверим. Возле каждого числа нарисуй соответствующее количество
Вот что получилось у меня. Сверь свои рисунки.
Отлично. Все числа знаешь. Но важно помнить, что существует определенная последовательность чисел, которую нельзя нарушать при пересчете предметов. Думаю, что этот порядок тебе уже знаком.
Посмотри еще раз на этот ряд чисел и расставь их в правильной последовательности.
7 3 5 2 4 1 0 9 6 10 8
Теперь проверим. Вот что должно получиться.
0 1 2 3 4 5 6 7 8 9 10
Числа располагаются в порядке возрастания, т.е. каждое следующее число больше всех предыдущих. Эта последовательность натуральных чисел основана на правиле образования чисел в пределах 10. Ты его уже знаешь.
Если к предыдущему числу прибавить еще один, то получим следующее число.
Отсюда получаем и обратное правило.
Если из числа вычесть один, то получим предыдущее число. Поэтому каждое число меньше всех последующих.
Теперь для сравнения чисел ты можешь использовать знания последовательности чисел. Например, 5 стоит после числа 3, значит 5 больше, чем три. А 7 стоит раньше, чем 10, значит 7 меньше, чем 10. Потренируйся самостоятельно составлять неравенства, глядя на ряд натуральных чисел.
А вот тебе задание посложнее: попробуй посчитать в обратном порядке. Это помогает лучше запомнить последовательность чисел в пределах десяти.
Уверена, что ты справился. Давай проверим: десять, девять, восемь, семь, шесть, пять, четыре, три, два, один. Все правильно, молодец.
А теперь попробуй восстановить порядок чисел, назвав пропущенные числа.
Молодец. Надеюсь ты все запомнил и скоро сможешь приступать к изучению новых чисел.
Десяток
А сейчас мы снова вернемся к нашему фокуснику. У него есть очень интересный волшебный ящик. Я расскажу, чем он особенный.
Фокусник положил в ящик морковь для кролика. Посчитай, сколько штук.
Правильно, он положил 3 морковки. Но в ящике ничего не произошло.
Фокусник положил еще несколько морковок. Посчитай, сколько теперь их.
Теперь в ящике 8 морковок. Но опять фокус не получился.
Тогда фокусник добавил еще две морковки. И теперь их стало 10. Пересчитай, чтобы проверить.
Убедился? Морковок стало ровно 10. И вдруг из ящика полетели искры. Фокусник достал из него морковку, но она оказалась связанной в пучок.
Фокусник решил продолжить и положил в ящик несколько конфет. Посчитай. Как думаешь, что произойдет?
Правильно, фокусник положил 5 конфет. А ящик бездействует.
Тогда фокусник добавил еще конфет, чтобы их стало 10. Вспомни состав числа 10. Это 5 и …?
Правильно, 10 – это 5 и 5.
Итак фокусник положил еще 5 конфет и теперь в ящике стало 10 конфет.
Догадался, что будет дальше?
Правильно, ящик сильно заискрил, и конфеты оказались упакованы в коробку.
Ты понял в чем суть волшебства? При каком условии работает волшебный ящик?
Верно. Когда в ящик попадает ровно 10 предметов, он их группирует в одну упаковку(пучок, коробку и т.п.).
В математике тоже используется такой фокус. Если предметов меньше 10 их считают по одному.
Полученное количество записывают в разряд единиц.
Когда предметов становится ровно 10 – они объединяются в более крупную счетную единицу, которая называется десяток:
1 десяток = 10 единиц.
Число десятков записывают в разряд десятков.
Мы в жизни часто встречаем ситуации, когда предметы складывают не по одному, а целыми десятками. Например:
Посмотри на картинки и скажи, сколько ты видишь отдельных палочек, а сколько десятков.
Верно, на картинке несколько десятков– их 5. А отдельных палочек – 7.
Теперь ты знаешь, что можно считать предметы не только по одному, но и целыми десятками. Эти знания тебе вскоре понадобятся, когда мы приступим к изучению двузначных чисел. Первое и наименьшее двузначное число ты сегодня выучил – это число 10. До встречи на следующем уроке.