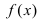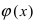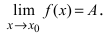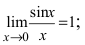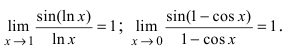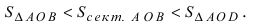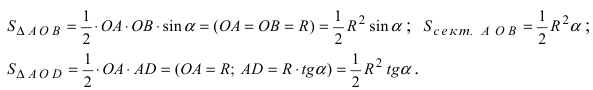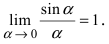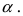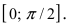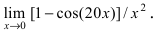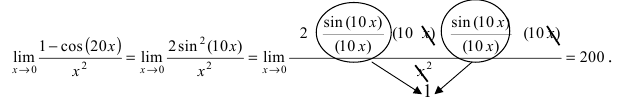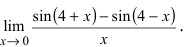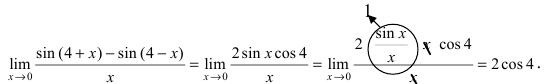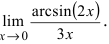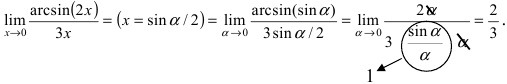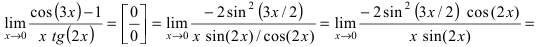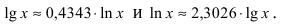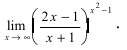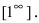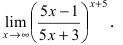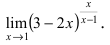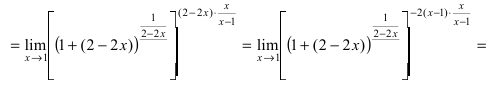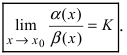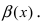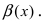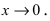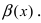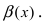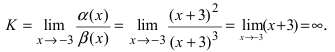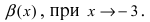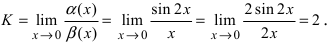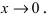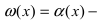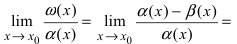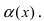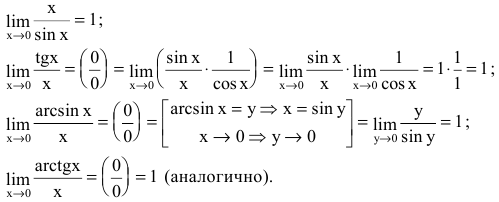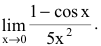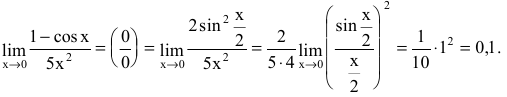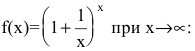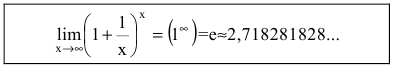Что такое первый и второй замечательные пределы
Замечательные пределы: Первый и второй замечательный предел.
Теперь со спокойной душой переходим к рассмотрению замечательных пределов.
Первый замечательный предел имеет вид .
Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 0.
Необходимо вычислить предел
Как видно, данный предел очень похож на первый замечательный, но это не совсем так. Вообще, если Вы замечаете в пределе sin, то надо сразу задуматься о том, возможно ли применение первого замечательного предела.
Согласно нашему правилу №1 подставим вместо х ноль:
Получаем неопределенность .
Теперь попробуем самостоятельно организовать первый замечательный предел. Для этого проведем нехитрую комбинацию:
Таким образом мы организовываем числитель и знаменатель так, чтобы выделить 7х. Вот уже и проявился знакомый замечательный предел. Желательно при решении выделять его:
Подставим решение первого замечательного примера и получаем:
Как видите – все очень просто.
Второй замечательный предел имеет вид , где e = 2,718281828… – это иррациональное число.
Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к .
Необходимо вычислить предел
Здесь мы видим наличие степени под знаком предела, значит возможно применение второго замечательного предела.
Как всегда воспользуемся правилом №1 – подставим вместо х:
Видно, что при х
основание степени
, а показатель – 4x >
, т.е. получаем неопределенность вида
:
Воспользуемся вторым замечательным пределом для раскрытия нашей неопределенности, но сначала надо его организовать. Как видно – надо добиться присутствия в показателе, для чего возведем основание в степень 3х, и одновременно в степень 1/3x, чтобы выражение не менялось:
Не забываем выделять наш замечательный предел:
Дальше знак предела перемещаем в показатель:
Вот такие действительно замечательные пределы!
Если у вас остались какие то вопросы по первому и второму замечательным пределам, то смело задавайте их в комментариях.
Всем по возможности ответим.
Также вы можете позаниматься с педагогом по этой теме.
Мы рады предложить вам услуги подбора квалифицированного репетитора в вашем городе. Наши партнеры оперативно подберут для вас хорошего преподавателя на выгодных для вас условиях.
Можно писать математические вычисления в блокнотах. В блокноты с логотипом (http://www.blocnot.ru) индивидуальным писать намного приятней.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
А пределы-то действительно замечательные. Я раньше такого понятия не встречала, но соглашусь, что название подобрано очень правильно. Я так понимаю, что для того, чтобы их использование облегчило решение, нужно их для начала просто «заметить» )))
Что-то я ничего замечательного в этих пределах не заметил. Почему их так называют? Потому что они давно доказаны? Так многие вещи в математике давно доказаны. И называют их аксиомами, если я не ошибаюсь
Ой, а что такое «замечательные пределы» и где вообще они используются? Я если честно, то услышал такое название в первые, потому что в школе точно не проходили. В институте так же не припомню всех этих тонкостей. Расскажите, когда они применяются в жизни?
В чем отличие первого от второго замечательных пределов? Понятно, что уравнения, но в чем их главная разница? И если есть отличия, то как найти их сразу, чтобы долго время не терять и не думать где правильно и где нет.
Содержание:
Замечательные пределы
Сравнение бесконечно малых функций
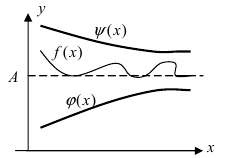
Признак существования предела (теорема о 2-х милиционерах)
Теорема: Если значения функции
значениями функций
Рассмотрим геометрический смысл данной теоремы (Рис. 62). Из рисунка видно, что в случае, когда функции 
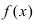
Рис. 62. Иллюстрация теоремы о “2-х милиционерах”.
Доказательство: Пусть 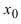
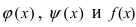
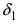
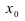
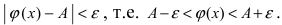
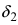
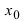
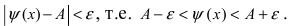
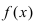
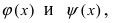
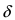
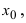
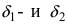
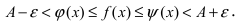
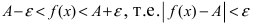
Первый замечательный предел
Определение: Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице, т.е. 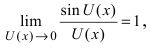
Пример:
Пределы являются первыми замечательными пределами
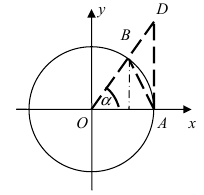
Доказательство: Для вывода этой формулы построим окружность с центром в точке О(0; 0) и радиусом R = 1. Выберем угол 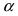
Рис. 63. Иллюстрация вывода формулы первого замечательного предела.
Из рисунка видно, что площади указанных фигу р связаны соотношением:
Вычислим эти площади
Следовательно, вышеприведенное неравенство приводится к виду 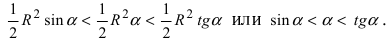
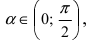
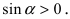
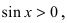
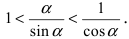
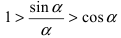
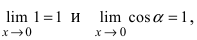
Аналогично проводится доказательство для любого значения угла
Таким образом, наличие в пределе, сводящемся к неопределенности 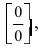
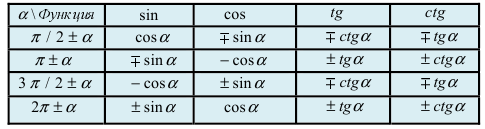
При вычислении первого замечательного предела используют следующие формулы:
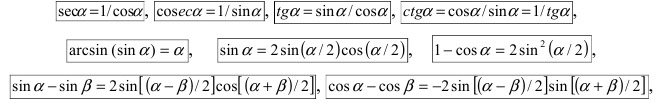
Табл. 1. Значения синуса и косинуса на интервале
Табл. 2. Формулы приведения.
Пример:
Найти
Решение:
При подстановке предельной величины переменной х имеем неопределенность 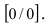
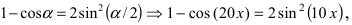
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 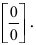
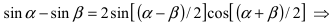
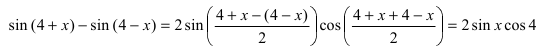
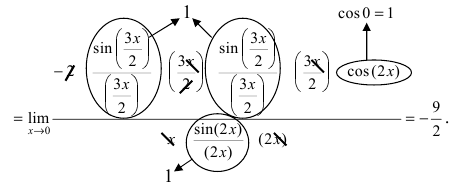
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 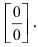
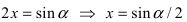
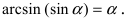
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределённость 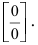
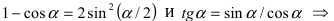
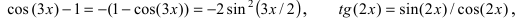
Число e и натуральные логарифмы. Второй замечательный предел
Рассмотрим логарифмическую функцию 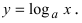
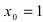
Определение: Натуральным логарифмом называется логарифм, для которого основание выбрано так, чтобы тангенс угла наклона касательной к положительному направлению оси абсцисс (Ох) был равен 1.
Основанием натурального логарифма является число 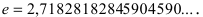
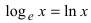
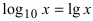
Определение: Вторым замечательным пределом называется предельное равенство 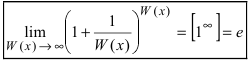
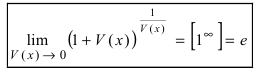
Замечание: Первая форма второго замечательного предела переходит во вторую с помощью замены 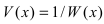
Замечание: Наличие неопределенности 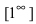
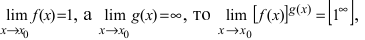
Пример:
Найти
Решение:
При подстановке предельного значения переменной х не имеем неопределенности
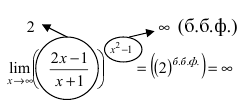
Пример:
Найти lim
Решение:
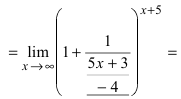
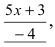
Пример:
Найти
Решение:
При подстановке предельного значения переменной х имеем неопределенность 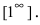
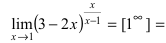
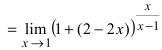
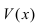
Сравнение бесконечно малых функций
Сравнить две бесконечно малые функции 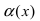
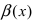
Определение: Если предел К не существует, то бесконечно малые функции 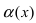
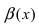
Пример:
Пусть 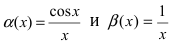
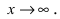
Решение:
Для доказательства вычислим предел 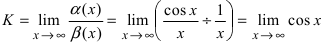
Определение: Если предел К равен нулю, то бесконечно малая функция 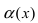
Пример:
Пусть 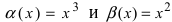
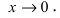
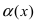
Решение:
Для доказательства вычислим предел 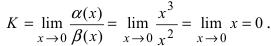
Определение: Если предел К равен 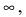
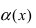
Пример:
Пусть 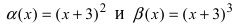
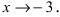
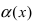
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малая функция 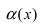
Определение: Если предел К равен конечному числу 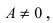
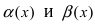
Пример:
Пусть 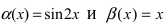
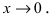
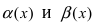
Решение:
Для доказательства вычислим предел
Следовательно, бесконечно малые функции 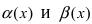
Определение: Если предел К равен 1, то бесконечно малые функции а(х) и Д(х) называются эквивалентными.
Пример:
Пусть 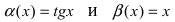
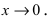
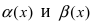
Решение:
Вычислим предел 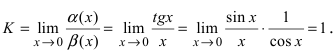

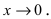
Теорема: Для того чтобы бесконечно малые функции 
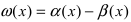

Доказательство:
1. Необходимость. Пусть бесконечно малая функция 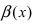
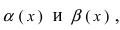
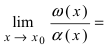
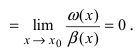
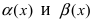
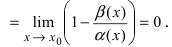
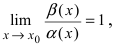
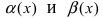
2. Достаточность. Пусть бесконечно малые функции 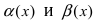
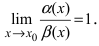
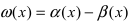
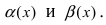
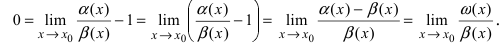
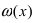
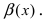
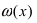
Замечание: При вычислениях одна бесконечно малая функция может быть заменена на эквивалентную бесконечно малую функцию. Например, функции 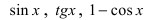
Замечательные пределы
Первый замечательный предел
Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:
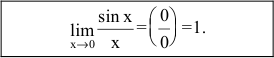
Пример №25
Найти
Решение:
Применим первый замечательный предел:
Второй замечательный предел
Числом е называется предел функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.