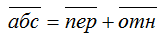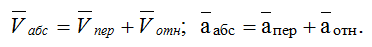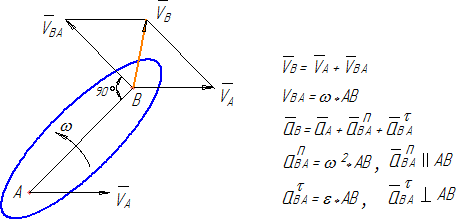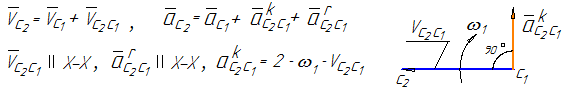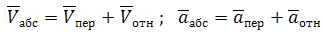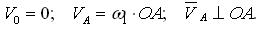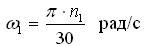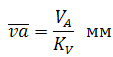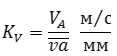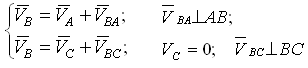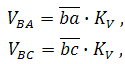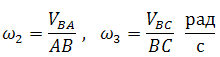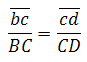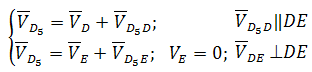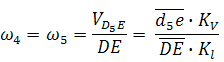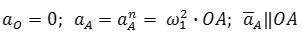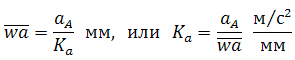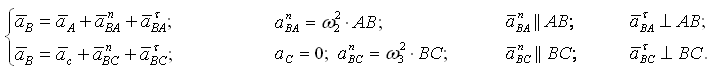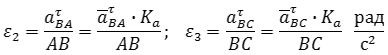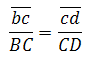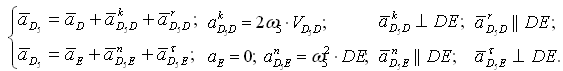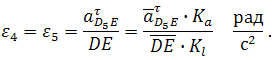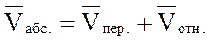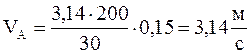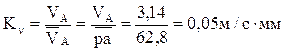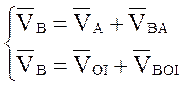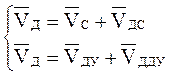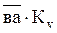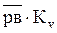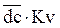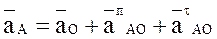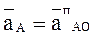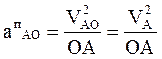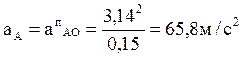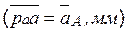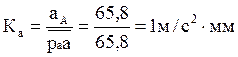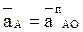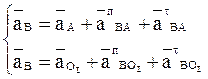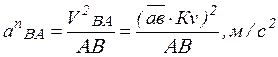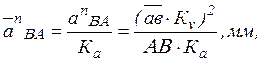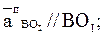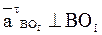Что такое план скоростей

iSopromat.ru

Метод планов скоростей и ускорений относится к графо-аналитическим методам исследования кинематики механизмов в теории механизмов и машин.

Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.

Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное — движение данной точки относительно той, движение которой принято за переносное:

Этот принцип в равной степени относится к перемещениям, скоростям и ускорениям:

Планы скоростей и ускорений обладают следующими свойствами:

При кинематическом исследовании плоских механизмов методом планов скоростей и ускорений встречается два случая:

1) две точки (одна исследуемая, вторая с известным законом движения, которое принимается в качестве переносного) принадлежат одному и тому же жесткому звену (рисунок 13).

В данном случае относительное движение этих точек получается за счет вращательного движения звена, на котором они находятся. При определении ускорений относительное ускорение раскладывается на нормальное (известное из физики как центростремительное – стремящееся к центру вращения) и тангенциальное.

Для примера, приведенного на рисунке 13, нормальное ускорение точки В относительно точки А будет направлено вдоль радиуса ВА к точке А. Тангенциальное – перпендикулярно этому радиусу;

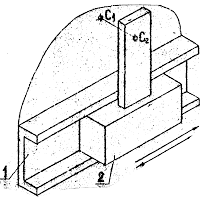
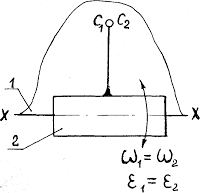
2) звенья соединяются поступательной парой. В этом случае рассматриваются две точки, совпадающие в данный момент времени по своему положению, но принадлежащие разным звеньям – одна ползуну, другая направляющей (рисунок 14).

Если известен закон движения направляющей 1, то известны характеристики движения любой точки на этом звене, в том числе и точки С₁, принадлежащей этой направляющей.

Движение точки С₁ принимается в качестве переносного. Движение точки С₂, принадлежащей ползуну, относительно точки С₁ получается за счет поступательного движения ползуна вдоль направляющей (влияние вращательного движения исключается, т.к. радиус вращения равен нулю – положение точек С₁ и С₂ совпадает). При определении ускорений кроме относительного ускорения, направленного вдоль направляющей, возникает кориолисово ускорение (см. рисунок 14).

Исследование кинематики механизма методом планов начинается с начального механизма (с входного звена) и далее ведется по группам Ассура в порядке их присоединения к механизму. Для каждой группы Ассура разработаны методы решения (уравнения и порядок построения планов), которые являются неизменными, независимо от того, в каком механизме данная группа Ассура находится.

Уравнения планов для групп Ассура второго класса приведены в таблице 3.1.

Таблица 3.1 – Кинематический анализ групп Ассура II класса методом планов

Источник

План скоростей

План скоросте́й — диаграмма, на которой векторы скоростей точек абсолютно твёрдого тела или некоторого механизма отложены из одной точки в выбранном масштабе.

План скоростей обладает следующими свойствами:

План скоростей позволяет графически решать задачи на нахождение скоростей точек тела. Чем крупнее выбранный масштаб, в котором построены векторы скоростей точек тела, тем точнее будет решена задача.

Пример решения задачи

Пусть имеется механизм АБВГ, состоящий из стержней, соединённых шарнирами. Пусть скорость точки В известна, и равна 2 м/с. Требуется найти скорость точки Б.

Заметим, что для нахождения скорости точки Б в рассмотренном примере необязательно знать длины звеньев механизма, важно знать только соотношения длин.

Эту же задачу можно решить с использованием понятия мгновенного центра скоростей.

См. также

Литература

Полезное

Смотреть что такое «План скоростей» в других словарях:

план скоростей механизма — Совокупность планов скоростей звеньев механизма с одним общим полюсом … Политехнический терминологический толковый словарь

план скоростей звена — Графическое построение, представляющее собою плоский пучок, лучи которого изображают абсолютные скорости точек звена плоского механизма, а отрезки, соединяющие концы лучей, относительные скорости соответствующих точек при данном положении звена … Политехнический терминологический толковый словарь

ПЛАН — (1) маркшейдерский графическое изображение в определённом масштабе и с достаточной подробностью геометрических элементов всех подземных выработок по отдельным пластам или горизонтам, а также геологических условий залегания пород, состояний… … Большая политехническая энциклопедия

ПОЛЮС — (1) особая, высшая, крайняя точка чего либо; (2) П. географический (Северный и Южный) воображаемая точка пересечения оси вращения Земли с земной поверхностью. Географические П. это единственные точки земной поверхности, не участвующие в суточном… … Большая политехническая энциклопедия

самолёт — летательный аппарат тяжелее воздуха с крылом, на котором при движении образуется аэродинамическая подъёмная сила, и силовой установкой, создающей тягу для полёта в атмосфере. Основные части самолёта: крыло (одно или два), фюзеляж, оперение, шасси … Энциклопедия техники

СССР. Технические науки — Авиационная наука и техника В дореволюционной России был построен ряд самолётов оригинальной конструкции. Свои самолёты создали (1909 1914) Я. М. Гаккель, Д. П. Григорович, В. А. Слесарев и др. Был построен 4 моторный самолёт… … Большая советская энциклопедия

Авиация — (франц. aviation, от латинского avis птица) летание на аппаратах тяжелее воздуха в околоземном воздушном пространстве. В 60 е гг. 20 в. в А. применяют Самолёты, Вертолёты, Планёры. Различают А. гражданскую, осуществляющую перевозки людей… … Большая советская энциклопедия

самолёт — … Энциклопедия «Авиация»

Источник

iSopromat.ru

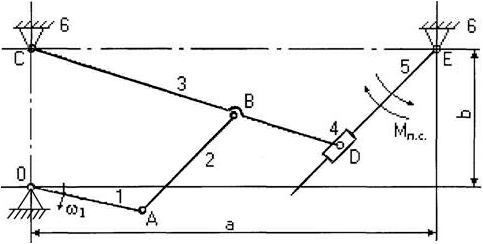
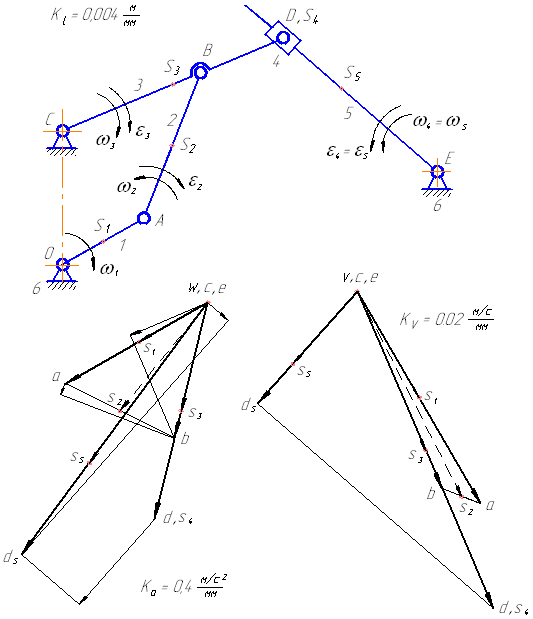
Рассмотрим порядок построения планов скоростей и ускорений точек звеньев на примере кинематического исследования плоского рычажного механизма (рисунок 1).

Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.

Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное – движение данной точки относительно той, движение которой принято за переносное:

На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана.

На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек.

Рисунок 1 – Кинематическая схема плоского рычажного механизма

Рассмотрим построение планов для механизма, представленного на рисунке 1. Вначале рассматривается начальный механизм, а далее решение ведется по группам Ассура в порядке их присоединения.

По вычисленному значению V_A выбираем масштаб плана скоростей K_V и из произвольного полюса откладываем отрезок va изображающий эту скорость:

Можно также назначать отрезок va а масштаб K_V вычислять:

Истинные значения (в м/с) относительных скоростей V_BA и V_BC определяются после построения плана умножением соответствующих отрезков (в мм) на масштаб плана:

а зная их, можно определить и угловые скорости звеньев 2 и 3:

Группа Ассура второго класса 3-го вида (звенья 4,5) :

Примечание: в данном случае размер DE является величиной переменной (т.е. в задании он отсутствует), поэтому в каждом положении механизма он определяется через отрезок на чертеже и масштаб длин.

План ускорений строится в таком же порядке.

Начальный механизм

Ускорение точки A состоит только из нормальной составляющей, т.к. задана постоянная угловая скорость первого звена ( ω₁=соnst ):

По вычисленному значению ускорения точки A выбирается масштаб плана ускорений и определяется отрезок на плане, соответствующий этому ускорению (или вычисляется масштаб плана ускорений по выбранному отрезку, изображающему ускорение точки A):

Здесь точка w – полюс плана ускорений.

Группа Ассура (звенья 2,3) второго класса 1-го вида:

Ускорение точки D определяем по подобию так же, как определяли скорость этой точки:

Рисунок 5 – Планы скоростей и ускорений для заданного положения механизма

Группа Ассура (звенья 4,5) второго класса 3-го вида:

При силовом расчете необходимо иметь ускорения центров масс ( a_si ), которые на плане ускорений определяются методом подобия.

Планы скоростей и ускорений для первого положения заданного механизма приведены на рисунке 5.

Уравнение планов скоростей и ускорений для каждой группы Ассура приведены в таблице 1.

Таблица 1 – Кинематический анализ групп Ассура II класса методом планов

Источник

Кинематическая схема механизма предназначена для определения положений, траекторий, скоростей и ускорений точек и звеньев механизма. Для построения кинематических схем используются условные обозначения согласно ГОСТ 2770 – 68.

Планы положений механизма строятся методом засечек в масштабе (рис.2). В отличие от масштабов, применяемых в машиностроении, в теории механизмов и машин масштабы представляют собой именованные числа. Масштабы обозначаются буквой К с соответствующим индексом:

Масштабы длин и пути 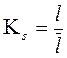, м /мм;

Масштаб скоростей 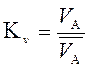, м/с.мм;

Численное значение масштаба должно быть либо десятичной дробью, либо целым числом и включать в себя стандартные цифры или комбинации цифр: 1, 2, 4, 5, 15, 25, 75, 10, 20…….

Для выполнения кинематического анализа данного механизма в задаче № 1 требуется вычертить в выбранном масштабе Кs положение механизма изображенное в задании и для него построить план скоростей и ускорений

1.2.2. Построение планов скоростей и ускорений

Метод построения планов скоростей и ускорений основан на теореме о разложении движения, согласно которой любое движение можно представить как сумму двух простых движений – переносного /поступательного/ и относительного /вращательного/. Тогда для скоростей:

,

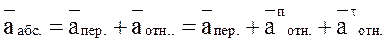
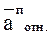
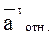
где — нормальная составляющая ускорения в относительном движении /определяется по данным плана скоростей/, на плане ускорений всегда направлена вдоль звена к центру относительного движения;

— касательная составляющая /определяется графически/ на плане ускорений, всегда направлена перпендикулярно к звену /радиусу/ относительного движения.

Для определения скорости или ускорения точки графическим путем не-обходимо составить систему из двух векторных уравнений. При составлении векторных уравнений движение точки рассматривается относительно двух других точек, с которыми эта точка связана и скорости которых уже известны.

Построить план скоростей и план ускорений для заданного положения механизма, изображенного на рисунке 2.

Пусть заданы размеры звеньев механизма: ОА = 150мм; АВ = 450мм и т.д. и частота вращения входного звена / кривошипа/ОА/, соответствующая n = 200 об/мин.

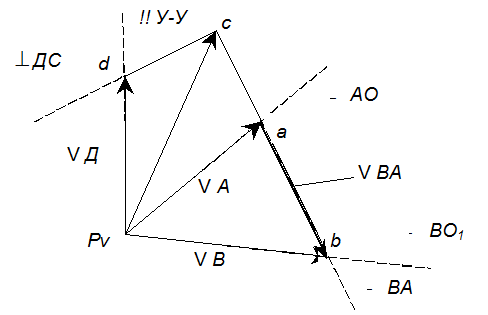
План скоростей рис.3.

Скорость пальца кривошипа /точка А/ определяется по формуле:

,

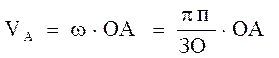
ОА – длина кривошипа, м;

Подставляя данные в формулу, получим:

Задаваясь длиной отрезка /мм/, изображающего на плане скоростей вектор скорости точки А, получим масштаб плана :

Отрезок :

= 62,8 мм

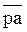
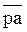
выбран так, чтобы был получен стандартный масштаб скоростей.

Рекомендуется выбирать отрезок 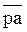не менее 50мм.

Из полюса плата скоростей р отложим вектор скорости точки А 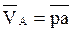перпендикулярно звену ОА/ по касательной к траектории движения точки А/ в сторону ее движения.

Рис.2. План механизма

.

Рис.3. План скоростей

Рис.4. План ускорений

Рассматривая движение точки В относительно точки А, а затем относительно О_I, имеем:

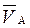
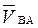
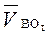
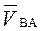
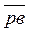
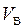
Из конца вектора скорости /точка а/ проводим линию действия вектора относительной скорости перпендикулярно звену АВ, а затем из полюса p /т.к. V₀ = 0/ перпендикулярно звену ВО_I проводим линию действия вектора относительной скорости до пересечения с линией действия вектора в точке в. Отрезокизображает вектор абсолютной скорости точки В .

Скорость точки С /третьей точки звена ВАС/ найдем методом подобия. Можно записать следующее соотношение:

или ,

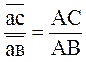
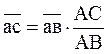
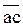
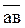
где и — отрезки на плане скоростей;

АС и АВ – размеры звеньев механизма.

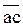
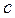
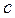
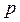
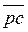
Вычислив отрезок и отложив его на плане скоростей, получим точку . Соединяя точку с полюсом , найдем отрезок , изображающий вектор абсолютной скорости точки С (V_c).

Для определения скорости точки Д рассмотрим движение этой точки относительно точек С и Д_у / точка Д_у принадлежит неподвижным направляющим и в данный момент совпадает с точкой Д /.

Система векторных уравнений имеет вид:

Так как V_ДУ =0, то .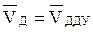

Абсолютные скорости каждой точки равны:

V_В = 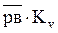, м/с

V_С = 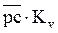, м/с

V_Д = 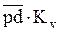, м/с

V_ВА =

=

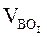
V_ДС =

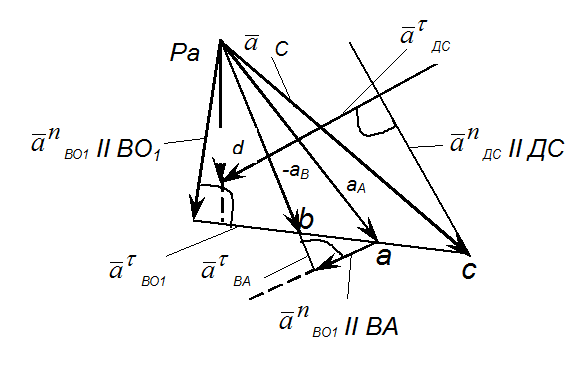
План ускорений рис.4.

Рассматривая движение точки А относительно точки О, можно записать:

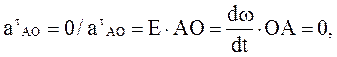
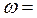
Ускорение а_о = 0, т.к. сonst. Следовательно, точка А при постоянной угловой скорости кривошипа будет иметь только нормальное / центральное/ ускорение:

Величина нормального ускорения:

Подставляя числовые значения, получим:

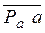
Задаваясь длиной отрезка изображаемого на плане ускорений вектор ускорения точки А, получим масштаб плана ускорений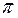

Отрезок 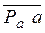выбран равным 65,8 мм, чтобы получить стандартный масштаб ускорений.

Из полюса плана ускорений откладываем вектор ускорения точки А

/отрезок / параллельно звену АО, направляя его от точки А к центру ее вращения – точке О.

Рассматривая движение точки В относительно точки А, а затем относительно точки О_1, имеем:

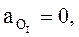
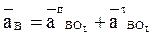
Так как то .

Нормальное ускорение В в ее относительном движении относительно точки А по величине определяется следующим образом:

Удобнее сразу находить величину отрезка, изображаемого вектор нормального ускорения:

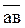
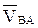
где — отрезок, изображений вектор относительной скорости на плане скоростей, мм;

АВ – длина шатуна, м.

Направлен вектор 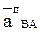по шатуну от точки В к точке А.

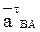
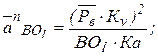
Вектор касательного ускорения известен только по направлению – линия его действия перпендикулярна звену ВА.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник