Что такое планиметрия 7 класс определение
Термины, определения и формулы по геометрии за 7 класс
Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).
В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.
Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Лучи называются сторонами угла, а точка — вершиной угла.
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности.
Радиус окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.
Отрезок, соединяющий две точки окружности, называется ее хордой.
Хорда, проходящая через центр окружности, называется диаметром.
Круг — это часть плоскости, ограниченная окружностью.
Угол называется развёрнутым, если обе его стороны лежат на одной прямой. ( Развёрнутый угол равен 180°).
Две геометрические фигуры называются равными, если их можно совместить наложением.
Середина отрезка — это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
Угол называется прямым, если он равен 90°.
Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.
Перпендикулярные прямые — прямые, которые при пересечении образуют прямой угол.
Параллельные прямые — прямые, лежащие в одной плоскости и не имеющие общих точек.
Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами треугольника.
Сумма углов треугольника равна 180°.
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Если все три угла треугольника острые, то треугольник называется остроугольным.
Если один из углов треугольника тупой, то треугольник называется тупоугольным.
Если один из углов треугольника прямой, то треугольник называется прямоугольным.
Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две стороны, образующие прямой угол — катетами.
(Т. о соотношениях между сторонами и углами треугольника) В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
В прямоугольном треугольнике гипотенуза больше катета.
(Признак равнобедр. треугольника) Если два угла треугольника равны, то треугольник равнобедренный.
(Т. Неравенство треугольника) Каждая сторона треугольника меньше суммы двух других сторон.
Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.
Первый признак равенства треугольников
«Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.»
Сокращенно его называют равенство «по двум сторонам и углу между ними».
На рисунке 1 представлен треугольник ABС. Который имеет три вершины (А, В и С). И стороны – АВ, АС и ВС.
Треугольники считаются равными, когда все их стороны и углы соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны, треугольники называются подобными). Таким образом очевидно, что равные треугольники можно наложить друг на друга – и они полностью совпадут.
Доказательство первого признака равенства треугольников
Два треугольника: ABC и DEF (рисунок 2).
По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т.е. ∠АСВ = ∠EFD).
Доказать, что треугольник ABC равен треугольнику DEF.
Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
При этом отрезки СА и СВ наложатся на отрезки FE и FD.
А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
Это в свою очередь даст совмещение вершин А и D, В и Е.
Следовательно, треугольники полностью совместятся, а значит, они равны.
Теорема доказана.
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Как и в доказательстве первого признака, нужно убедиться, достаточно ли этого для равенства треугольников, можно ли их полностью совместить?
1. Так как MN=PR, то эти отрезки совмещаются, если совместить их конечные точки.
2. Так как∡N=∡R и∡M=∡P, то лучи MK и NK наложатся соответственно на лучи PT и RT.
3. Если совпадают лучи, то совпадают точки их пересечения K и T.
4. Совмещены все вершины треугольников, то есть ΔMNK и ΔPRT полностью совместятся, значит они равны.
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Опять попробуем совместить треугольникиΔMNK и ΔPRT наложением и убедится, что соответственно равные стороны гарантирует и равенство соответственных углов этих треугольников и они полностью совпадут.
Совместим, например, одинаковые отрезки MK иPT. Допустим, что точки N и R при этом не совмещаются.
Пусть O — середина отрезка NR. Соответственно данной информацииMN=PR, KN=TR. Треугольники MNR и KNR равнобедренные с общим основанием NR.
Поэтому их медианы MO и KO являются высотами, значит перпендикулярны NR. Прямые MO и KO не совпадают, так как точки M, K, O не лежат на одной прямой. Но через точку O прямой NR можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.
Доказано, что должны совместиться и вершины N и R.
Третий признак позволяет назвать треугольник очень сильной, устойчивой фигурой, иногда говорят, что треугольник — жёсткая фигура. Если длины сторон не меняются, то углы тоже не меняются. Например, у четырёхугольника такого свойства нет. Поэтому разные поддержки и укрепления делают треугольными.
Перпендикуляр к прямой
Из точки не лежащей на прямой можно провести перпендикуляр к этой прямой и притом только один
Медианы,биссектриссы и высоты треугольника
В любом треугольнике медианы пересекаются в одной точке. Биссектрисы пересекаются в одной точке. Высоты или их продолжения также пересекаются в одной точке
Свойства равнобедренного треугольника
Признаки параллельности двух прямых. Теорема 1
Если при пересечении двух прямых секущей накрест лежащие углы равны то прямые параллельны.
Признаки параллельности прямых.Теорема 2
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Признаки параллельности прямых. Теорема 3.
Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰ то прямые параллельны.
Теорема об углах образованных двумя параллельными прямыми и секущей.
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Аксиома параллельных прямых.
В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.
Теоремы об углах, образованных двумя параллельными прямыми и секущей
Теорема Сумма углов треугольника равна 180°.
Рассмотрим произвольный треугольник KLM и докажем, что ∡K+∡L+∡M=180°.
Проведём через вершину L прямую a, параллельную стороне KM.
Углы, обозначенные 1, являются накрест лежащими углами при пересечении параллельных прямых a и KMсекущей KL, а углы, обозначенные 2 — накрест лежащими углами при пересечении тех же параллельных прямых секущей ML.
Очевидно, сумма углов 1, 2 и 3 равна развёрнутому углу с вершиной L, т. е.
∡1+∡2+∡3= 180°или ∡K+∡L+∡M=180°.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
Следствие 3. В равностороннем треугольнике каждый угол равен 60°.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Из равенств ∡KML+∡BML= 180° и ∡K+∡L+∡KML=180° получаем, что ∡BML=∡K+∡L.
Четырёхугольники
Многоугольник — фигура, состоящая из нескольких точек плоскости, поочередно соединённых между собой непересекающимися отрезками.
Выпуклый многоугольник — это многоугольник, который весь лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Теорема:Сумма внутренних углов выпуклого n-угольника равна (n-2)*1800.
Параллелограмм- это четырёхугольник, у которого противоположные стороны попарно параллельны.
Свойство:в параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство:диагонали параллелограмма точкой пересечения делятся пополам.
Теорема(признакпараллелограмма): Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма): Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма): Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.Параллельные стороны-основания, непараллельные стороны-боковые.
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Прямоугольная трапеция — это трапеция, у которой один из углов прямой.
Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пресекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
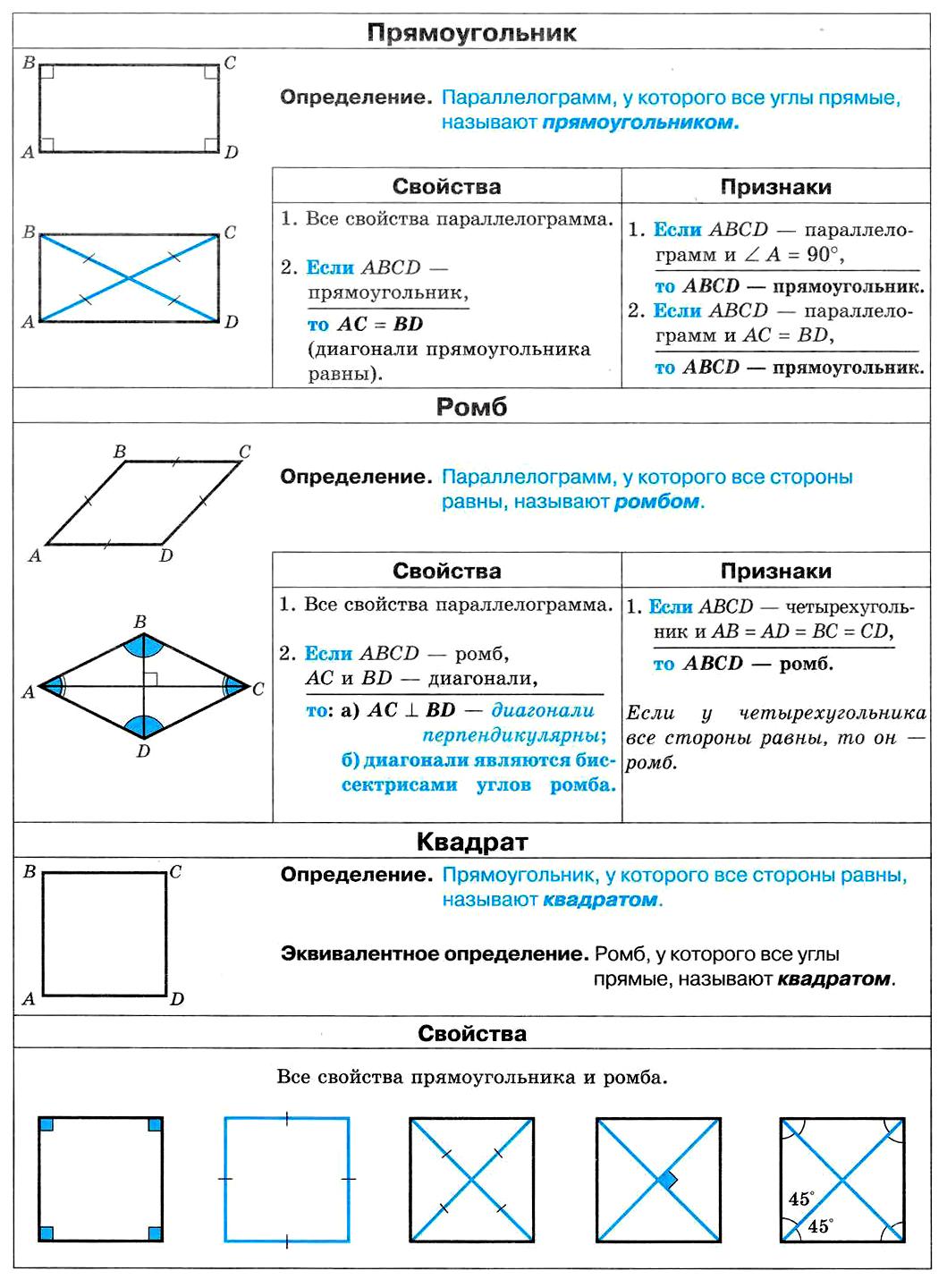
Прямоугольник — это параллелограмм, у которого все углы прямые.
Свойство: диагонали прямоугольника равны.
Теорема(признакпрямоугольника): если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Ромб — это параллелограмм, у которого все стороны равны.
Свойство: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат — это прямоугольник, у которого все стороны равны.
Площадь
Площадь плоской фигуры-это количество единичных квадратов, вмещающихся в данную фигуру.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его смежных сторон.
Площадь параллелограмма равна произведению его основания на высоту.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна произведению его катетов.
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции равна полусумме её оснований на высоту.
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема(обр.): если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.
Подобные треугольники
Отрезки m и n пропорциональны отрезкам m1и n1,если отношения их длин равны m:m1= n: n1.
Подобные треугольники — это треугольники,у которых соответственные углы равны, а сходственные стороны пропорциональны.
Коэффициент подобия — это число, равное отношению сходственных сторон подобных треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Свойство биссектрисы тр-ка: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Теорема(первый признак подобия треугольников): если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Теорема(второй признак подобия треугольников): если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Теорема(первый признак подобия треугольников): если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Среднее пропорциональное(среднее геометрическое)двух величин – это квадратный корень из произведения этих величин.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
С. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,заключённым между катетом и высотой, проведённой из вершины прямого угла.
Синус острого угла прямоугольного треугольника — это отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника- это отношение прилежащего катета к гипотенузе.
Окружность
Касательная к окружности – это прямая, имеющая с окружностью только одну общую точку.
Т. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Т.(обр.) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Центральный угол – это угол с вершиной в центре окружности.
Дуга окружности измеряется центральным углом, который на неё опирается.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Т.Вписанный угол равен половине дуги, на которую он опирается.
С. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
С. Вписанный угол, опирающийся на полуокружность, — прямой.
Т. Если две хорды окружности пересекаются, произведение отрезков одной хорды равно произведению отрезков другой хорды.
Планиметрия
Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости.
Первое систематическое изложение планиметрии впервые было дано Евклидом в его труде «Начала».
Содержание
Изучение в школьном курсе
При систематическом изучении школьного курса геометрии обычно начинают с изучения планиметрии, а затем приступают к изучению стереометрии, изучающей пространственные фигуры. Основными понятиями школьного курса планиметрии являются точка, прямая, плоскость и расстояние (между двумя точками или от точки до точки), а также некоторые общематематические понятия, такие, как множество, отображение множества на множество и некоторые другие.
Содержание школьного курса из года в год несколько меняется, однако его ядро остаётся в целом неизменным. Планиметрия содержит:
Были попытки излагать обе части геометрии (планиметрию и стереометрию) вместе, слитно, изучая плоские и пространственные фигуры одновременно.
Фигуры, изучаемые планиметрией
См. также
Ссылки
Литература
Задачники
| Геометрия | Алгебраическая геометрия • Аналитическая геометрия • Евклидова геометрия • Неевклидова геометрия • Планиметрия • Стереометрия • Тригонометрия |
|---|---|
| Топология | Общая топология • Алгебраическая топология |
| Смежные направления | Дифференциальная геометрия и топология • Геометрическая топология |
Полезное
Смотреть что такое «Планиметрия» в других словарях:
планиметрия — планиметрия … Орфографический словарь-справочник
ПЛАНИМЕТРИЯ — (от лат. planus плоский, и греч. metreo меряю). Часть геометрии, занимающаяся исследованием и измерением фигур на плоскости. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЛАНИМЕТРИЯ от лат. planus, плоский, и… … Словарь иностранных слов русского языка
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, планировать и пр. см. план. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, подраздел ГЕОМЕТРИИ, в которой линии, углы и фигуры представлены в двухмерной форме, т.е. на плоскости. В планиметрии действуют аксиомы ЕВКЛИДА … Научно-технический энциклопедический словарь
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, планиметрии, мн. нет, жен. (от лат. planum плоскость и греч. metreo мерю) (мат.). Отдел элементарной геометрии, изучающий фигуры на плоскости. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, и, жен. Часть геометрии, изучающая фигуры на плоскости. | прил. планиметрический, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
планиметрия — сущ., кол во синонимов: 2 • геометрия (9) • математика (29) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, измерение площадей плоскостных фигур, очень часто применяемое в мед. физиол. исследовательских работах, преиму i щественно по отношению к площадям кривых, записанных на кимографе. Такое измерение можно производить или с помощью… … Большая медицинская энциклопедия
Планиметрия — основные понятия и аксиомы
Представь, что ты вдруг очутился на другой планете, ну или… в компьютерной игре.
Перед тобой набор неизвестных продуктов, а твоя задача – приготовить из этого набора как можно больше вкусных блюд. Что тебе понадобится?
Конечно же, правила, инструкции – что можно делать с теми или иными продуктами. А то вдруг ты сваришь то, что едят только в сыром виде или, наоборот, положишь в салат то, что непременно нужно варить или жарить? Так что, без инструкций – никуда!
Хорошо, но к чему такое вступление? При чем тут геометрия? Понимаешь, великое множество утверждений о всяких фигурах в геометрии и есть то самое множество «блюд», которые мы должны научиться готовить.
Но из чего? Из основных объектов геометрии! А вот инструкция по их «употреблению» называется умными словами «система аксиом».
Планиметрия — коротко о главном
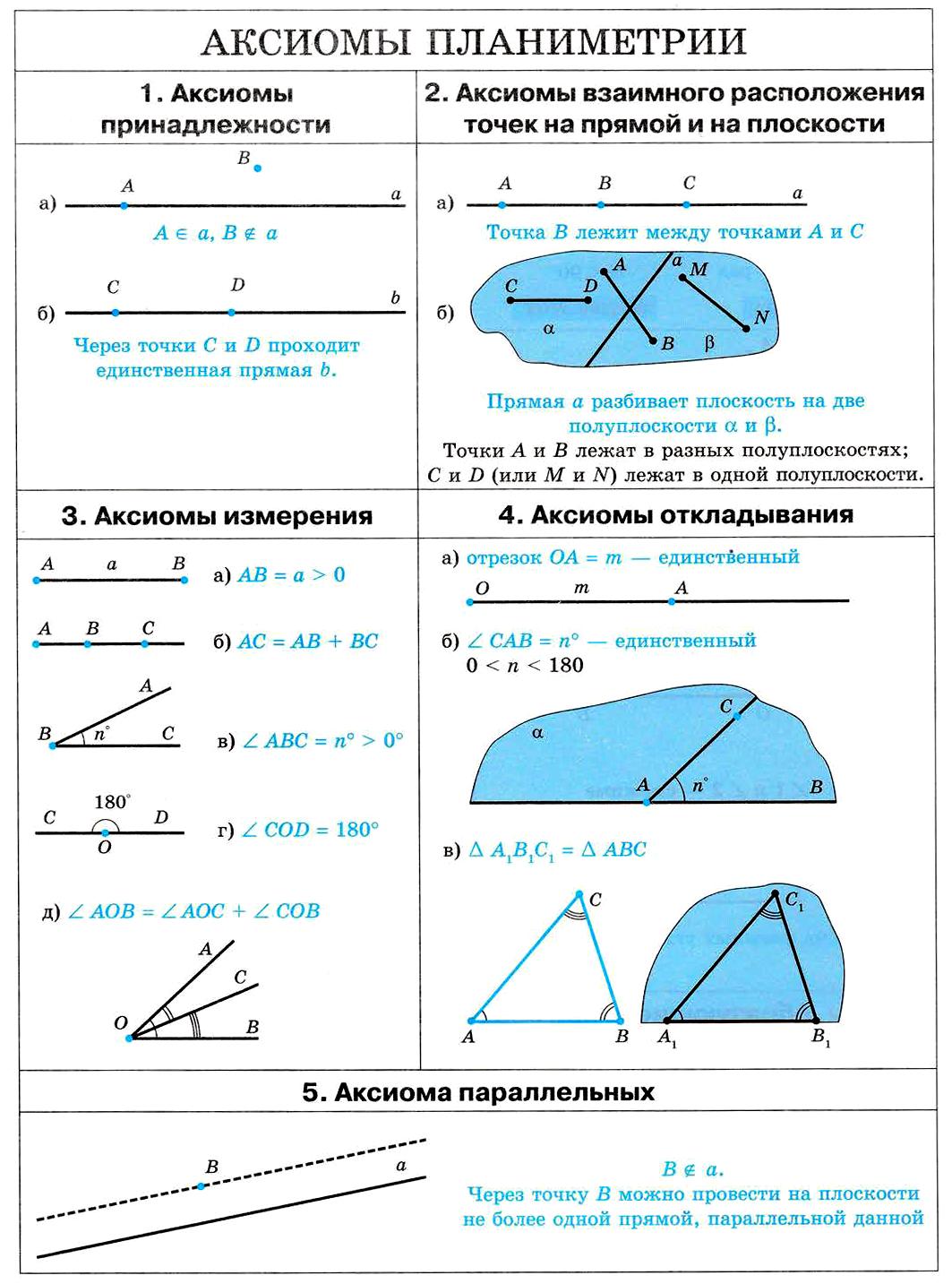
Аксиомы принадлежности:
Аксиомы порядка:
Аксиомы мер для отрезков и углов:
Аксиомы существования треугольника, равного данному:
Следствие 1. От данной точки данной прямой в данную сторону можно отложить отрезок данной длины, причем единственным образом
Следствие 2. От данного луча в данную полуплоскость можно отложить угол данной величины, причем единственным образом
Аксиома параллельных:
Основные факты об углах:
Теорема. Сумма смежных углов равна \( \displaystyle 180<>^\circ \).
\( \displaystyle 180<>^\circ=x_<1>^<<>^\circ >+x_<2>^<<>^\circ >\)
Теорема. Вертикальные углы равны.
\( \displaystyle \angle 1=\angle 2\).
Что такое планиметрия 7 класс определение
Аксиомы принадлежности. Аксиомы взаимного расположения точек на прямой и плоскости. Аксиомы измерения. Аксиомы откладывания. Аксиома параллельных
02. Углы
Смежные углы. Вертикальные углы. Углы при пересечении
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
04. Свойства сторон и углов треугольника
Свойства сторон и углов треугольника. Внешний угол. Свойства. Неравенство треугольника. Равнобедренный треугольник
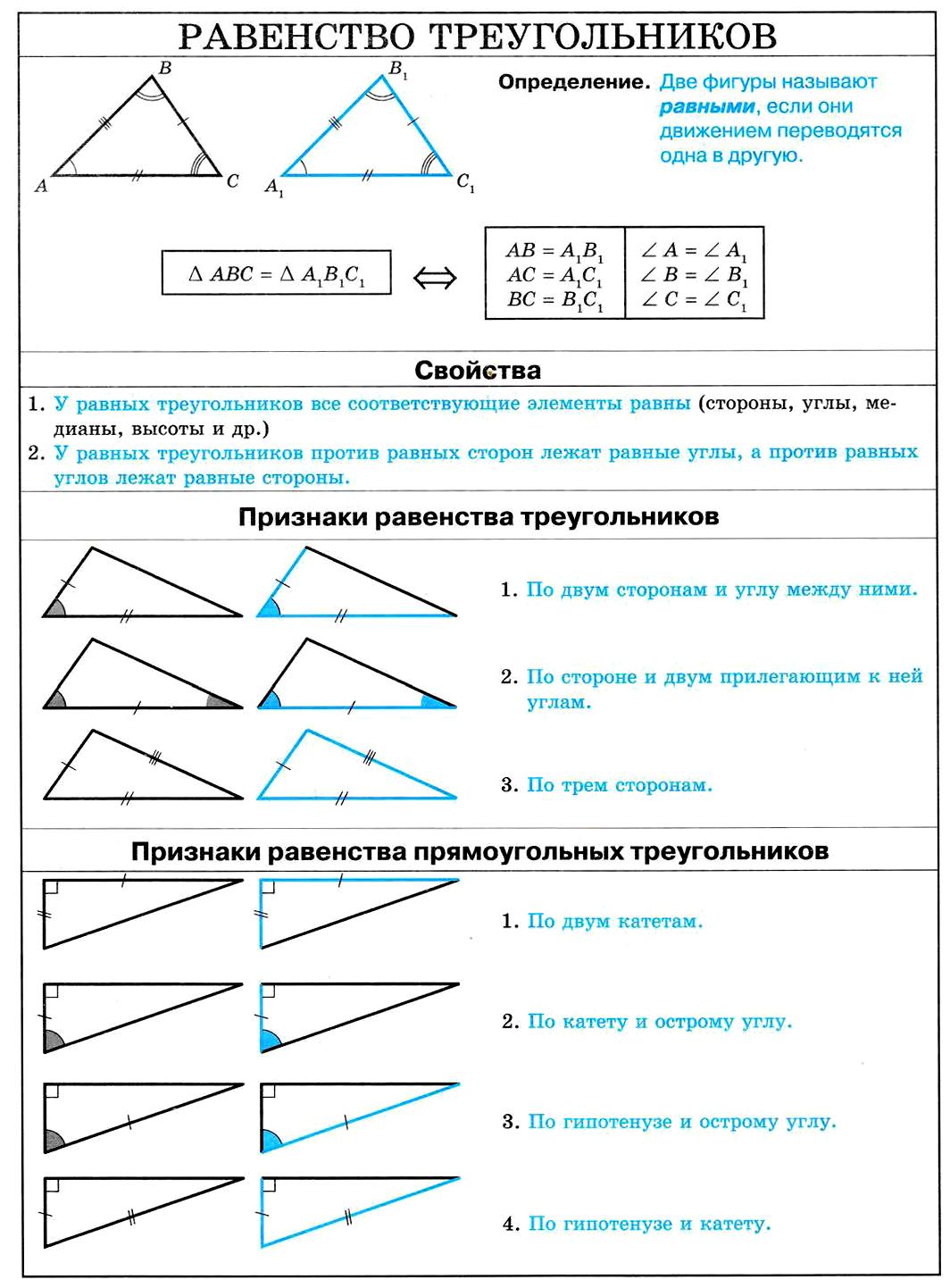
05. Равенство треугольников.
Равенство треугольников. Свойства. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников
06. Медиана треугольника.
Медиана треугольника. Свойства.
07. Биссектриса треугольника.
Биссектриса треугольника. Свойства
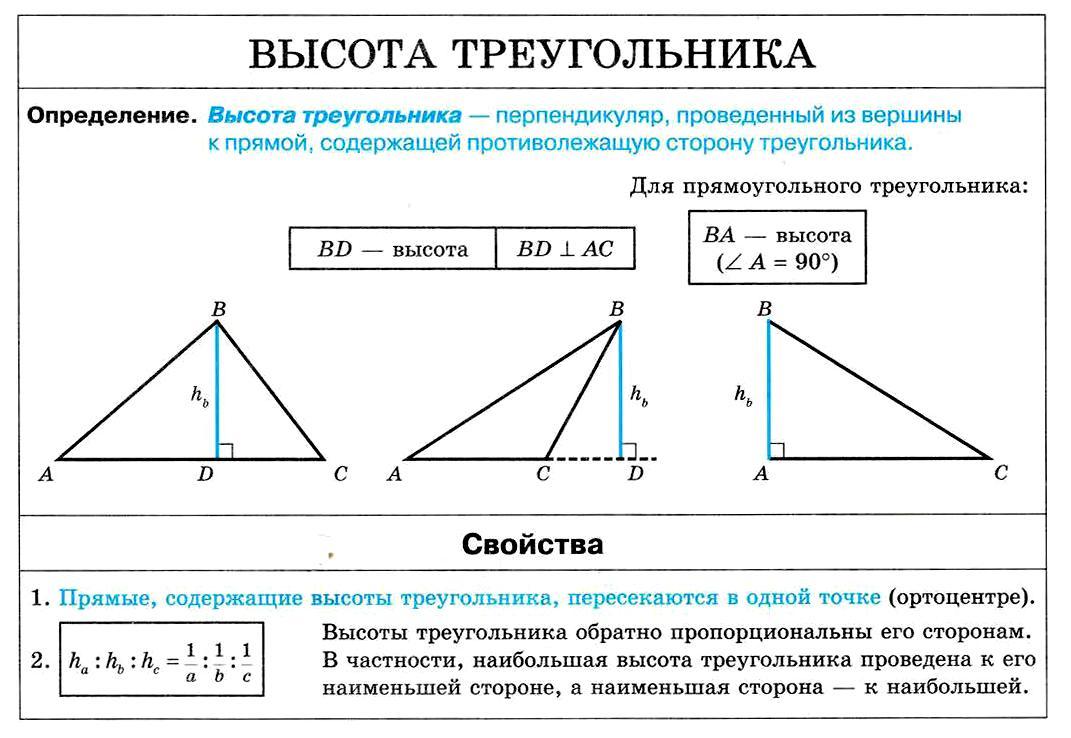
08. Высота треугольника
Высота треугольника. Свойства
09. Средняя линия треугольника
Средняя линия треугольника. Свойства
10. Соотношение между элементами прямоугольного треугольника
Соотношение между элементами прямоугольного треугольника
11. Соотношение между сторонами и углами в произвольном треугольнике
Соотношение между сторонами и углами в произвольном треугольнике
12. Преобразование фигур. Движение
Преобразование фигур. Движение. Симметрия относительно точки. Поворот. Симметрия относительно прямой. Параллельный перенос
13. Преобразование подобия
Преобразование подобия. Свойства. Гомотетия.
14. Подобие треугольников.
Подобие треугольников. Свойства. Признаки подобия треугольников
15. Параллелограмм и его виды.
Параллелограмм и его виды. Свойства. Признаки
Прямоугольник. Ромб. Квадрат.
16. Трапеция
Трапеция. Частные случаи трапеции. Средняя линия трапеции. Дополнительные построения для трапеции
17. Окружность, хорды и дуги
Окружность, хорды и дуги. Свойства
18. Окружность. Касательные и секущие.
Окружность. Касательные и секущие.
19. Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
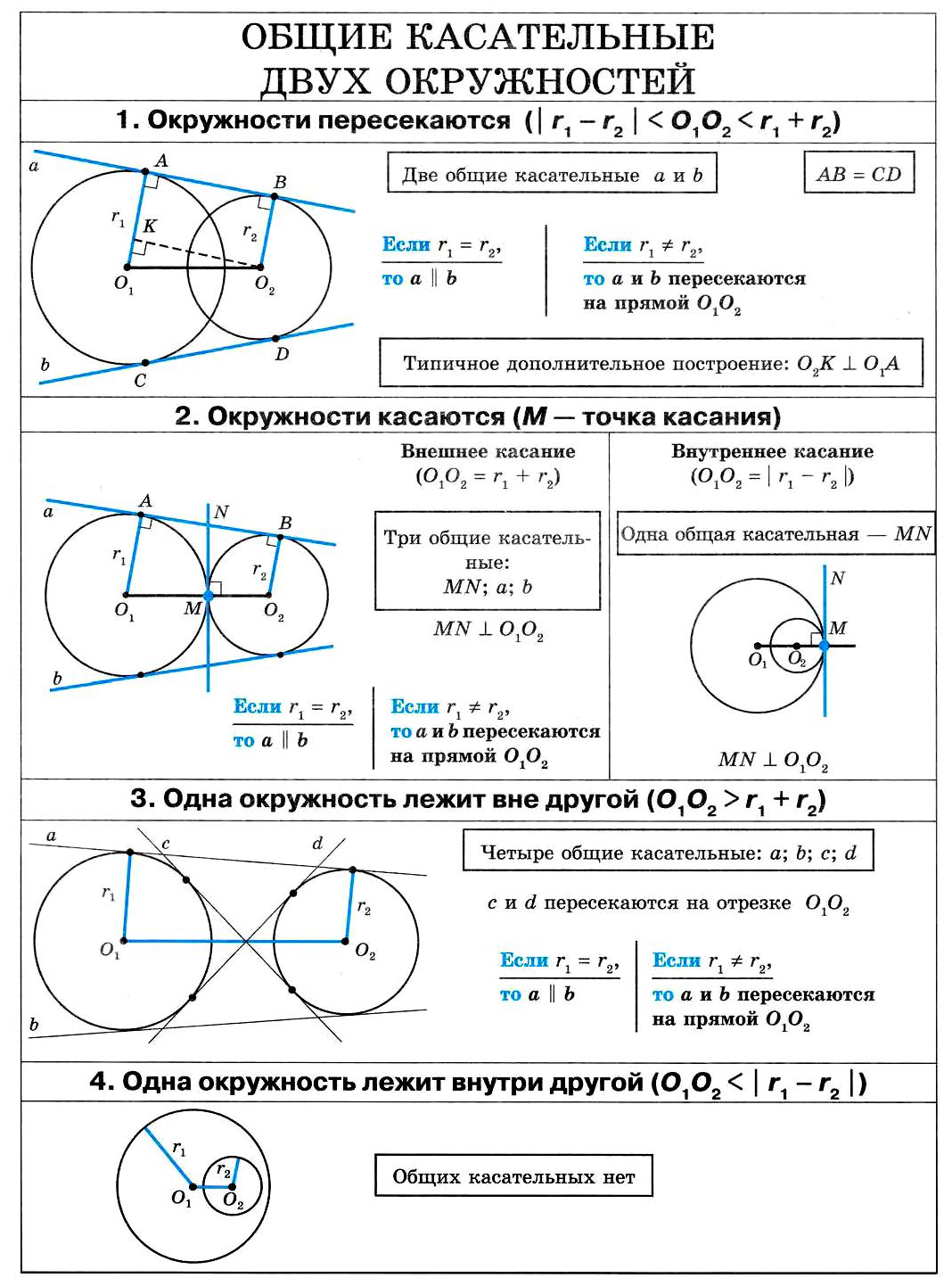
20. Общие касательные двух окружностей.
Общие касательные двух окружностей.
21. Углы в окружности.
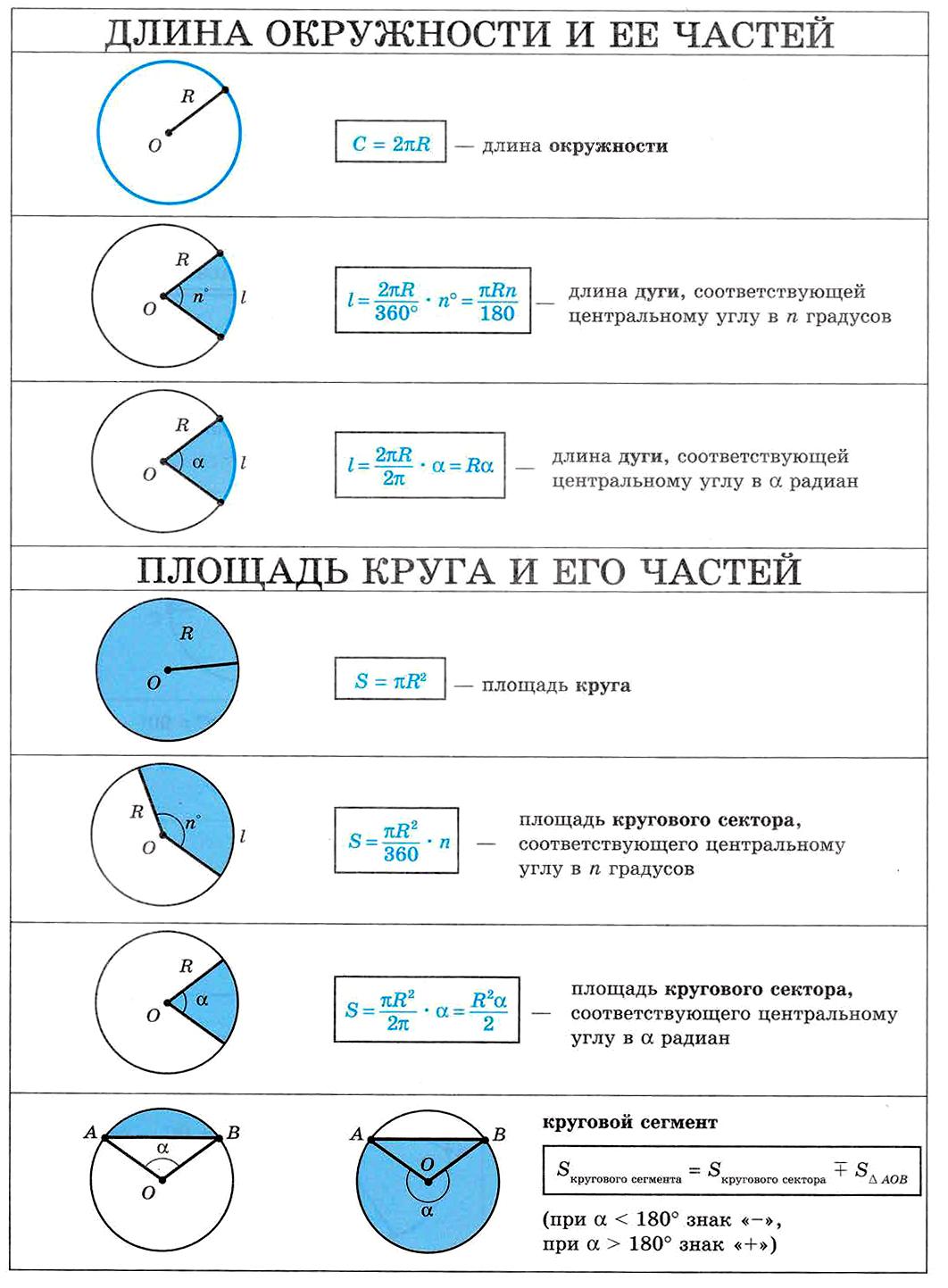
22. Длина окружности и её частей. Площадь круга и его частей
Длина окружности и её частей. Площадь круга и его частей
23. Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
24. Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
25. Окружности, описанные и вписанные в правильные многоугольники
Окружности, описанные и вписанные в правильные многоугольники
26. Площади треугольников.
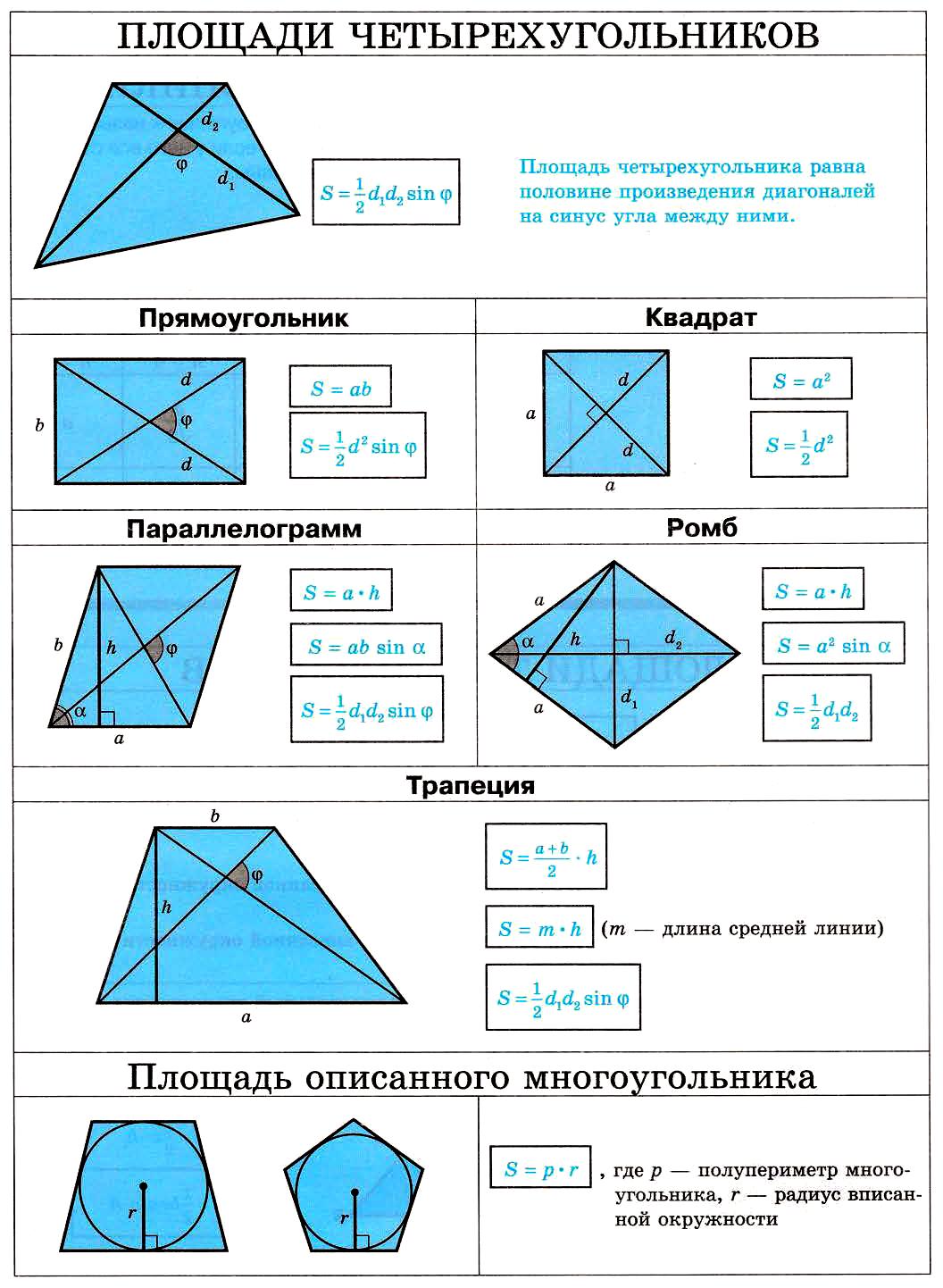
27. Площади четырехугольников.
Площади четырехугольников. Площадь описанного многоугольника
Вы смотрели справочник по геометрии для 7-11 классов «Теоремы и определения по Планиметрии».
2 Комментарии
Огромное спасибо за такую обширную базу по планиметрии. Конечно, сюда можно добавить ещё пару формул, но это самая полная шпаргалка по планиметрии, которую я знаю.
Отличный справочник по планиметрии! Благодарю!
Добавить комментарий Отменить ответ
Конспекты по геометрии:
7 класс
8 класс
9 класс
Найти конспект:
О проекте
Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Возрастная категория: 12+
(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!