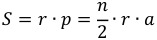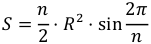Что такое планиметрия кратко
Планиметрия
Смотреть что такое «Планиметрия» в других словарях:
планиметрия — планиметрия … Орфографический словарь-справочник
Планиметрия — (от лат. planum «плоскость», др. греч. μετρεω «измеряю») раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Первое… … Википедия
ПЛАНИМЕТРИЯ — (от лат. planus плоский, и греч. metreo меряю). Часть геометрии, занимающаяся исследованием и измерением фигур на плоскости. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЛАНИМЕТРИЯ от лат. planus, плоский, и… … Словарь иностранных слов русского языка
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, планировать и пр. см. план. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, подраздел ГЕОМЕТРИИ, в которой линии, углы и фигуры представлены в двухмерной форме, т.е. на плоскости. В планиметрии действуют аксиомы ЕВКЛИДА … Научно-технический энциклопедический словарь
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, планиметрии, мн. нет, жен. (от лат. planum плоскость и греч. metreo мерю) (мат.). Отдел элементарной геометрии, изучающий фигуры на плоскости. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, и, жен. Часть геометрии, изучающая фигуры на плоскости. | прил. планиметрический, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
планиметрия — сущ., кол во синонимов: 2 • геометрия (9) • математика (29) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, измерение площадей плоскостных фигур, очень часто применяемое в мед. физиол. исследовательских работах, преиму i щественно по отношению к площадям кривых, записанных на кимографе. Такое измерение можно производить или с помощью… … Большая медицинская энциклопедия
Что такое планиметрия кратко
При решении задач по геометрии помимо всех геометрических формул и свойств, которые будут приведены ниже, нужно очень хорошо помнить основные формулы по тригонометрии. Укажем для начала несколько основных свойств различных типов углов:
Теперь перейдем к свойствам треугольника. Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Запомните также, что сумма любых двух сторон треугольника всегда больше третьей стороны. Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Важно знать: Центр вписанной в треугольник окружности лежит на пересечении биссектрис (все три биссектрисы пересекаются в этой одной точке). Формулы биссектрисы:
Все три высоты в треугольнике пересекаются в одной точке. Положение точки пересечения определяется типом треугольника:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Трапеция
Некоторые свойства трапеций:
Параллелограмм
Площадь параллелограмма через две стороны и угол между ними:
Некоторые свойства параллелограмма:
Квадрат
Площадь квадрата через длину его диагонали:
Свойства квадрата – это все свойства параллелограмма, ромба и прямоугольника одновременно.
Ромб и прямоугольник
Свойства ромба:
Свойства прямоугольника:
Произвольные фигуры
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):
Обобщённая теорема Фалеса: Параллельные прямые отсекают на секущих пропорциональные отрезки.
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Многоугольники
Выпуклым многоугольником называется многоугольник, обладающий тем свойством, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Сумма внутренних углов плоского выпуклого n-угольника равна:
Число диагоналей всякого многоугольника равно (где: n – число сторон):
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны между собой равны и все углы между собой равны. Внутренний угол правильного многоугольника равен:
Центральный угол правильного n-угольника равен:
Площадь правильного многоугольника с числом сторон n, длиной стороны a, радиусом описанной окружности R, полупериметром p и радиусом вписанной окружности r, может быть рассчитана по следующим формулам:
Окружность
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь кругового сегмента:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.
Планиметрия
Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости.
Первое систематическое изложение планиметрии впервые было дано Евклидом в его труде «Начала».
Содержание
Изучение в школьном курсе
При систематическом изучении школьного курса геометрии обычно начинают с изучения планиметрии, а затем приступают к изучению стереометрии, изучающей пространственные фигуры. Основными понятиями школьного курса планиметрии являются точка, прямая, плоскость и расстояние (между двумя точками или от точки до точки), а также некоторые общематематические понятия, такие, как множество, отображение множества на множество и некоторые другие.
Содержание школьного курса из года в год несколько меняется, однако его ядро остаётся в целом неизменным. Планиметрия содержит:
Были попытки излагать обе части геометрии (планиметрию и стереометрию) вместе, слитно, изучая плоские и пространственные фигуры одновременно.
Фигуры, изучаемые планиметрией
См. также
Ссылки
Литература
Задачники
| Геометрия | Алгебраическая геометрия • Аналитическая геометрия • Евклидова геометрия • Неевклидова геометрия • Планиметрия • Стереометрия • Тригонометрия |
|---|---|
| Топология | Общая топология • Алгебраическая топология |
| Смежные направления | Дифференциальная геометрия и топология • Геометрическая топология |
Полезное
Смотреть что такое «Планиметрия» в других словарях:
планиметрия — планиметрия … Орфографический словарь-справочник
ПЛАНИМЕТРИЯ — (от лат. planus плоский, и греч. metreo меряю). Часть геометрии, занимающаяся исследованием и измерением фигур на плоскости. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЛАНИМЕТРИЯ от лат. planus, плоский, и… … Словарь иностранных слов русского языка
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, планировать и пр. см. план. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, подраздел ГЕОМЕТРИИ, в которой линии, углы и фигуры представлены в двухмерной форме, т.е. на плоскости. В планиметрии действуют аксиомы ЕВКЛИДА … Научно-технический энциклопедический словарь
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, планиметрии, мн. нет, жен. (от лат. planum плоскость и греч. metreo мерю) (мат.). Отдел элементарной геометрии, изучающий фигуры на плоскости. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, и, жен. Часть геометрии, изучающая фигуры на плоскости. | прил. планиметрический, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
планиметрия — сущ., кол во синонимов: 2 • геометрия (9) • математика (29) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, измерение площадей плоскостных фигур, очень часто применяемое в мед. физиол. исследовательских работах, преиму i щественно по отношению к площадям кривых, записанных на кимографе. Такое измерение можно производить или с помощью… … Большая медицинская энциклопедия
Что такое планиметрия? Знакомство с геометрией
Геометрия – предмет интересный и, без сомнения, очень полезный. Он заставляет креативно мыслить, находить нестандартные решения, представлять различные фигуры и т. д. Очень часто одну задачу в геометрии можно решить несколькими способами. Но первое, с чем имеют дело школьники, начиная знакомство с геометрией, – это планиметрия. Что такое планиметрия? И почему изучение геометрии начинается с нее?
Что такое планиметрия? Определение в геометрии
Планиметрия – это раздел геометрии, изучающий фигуры, которые можно расположить в пределах одной плоскости. Например, квадрат, начерченный на листке бумаги, будет относиться к планиметрии.
Планиметрия – это первый шаг школьников к близкому знакомству с геометрией. Именно в планиметрии они узнают о существовании таких понятий, как отрезок, прямая, точка, направление, плоскость и т. д. Для дальнейшего движения в освоении геометрии школьники усваивают, что такое планиметрия. Для них это основа основ. Происходит первое знакомство с теоремами, аксиомами, новыми терминами, явлениями.
Происхождение слова
Как и многие другие термины, слово «планиметрия» берет свое начало в латинском языке. В переводе оно означает «плоскость», «измеряю». Еще древнегреческие философы ввели его в употребление и дали ему определение. Что такое планиметрия, сейчас знает каждый школьник, ведь с нее начинается изучение геометрии.
Планиметрию относят к Евклидовой геометрии или, как ее еще называют, элементарной геометрии. Евклид – древнегреческий философ, а его главный труд – «Начало» – считается вершиной античной математики. Работы этого философа определили ход развития математики и были предметом изучения и обсуждений в течение очень многих лет.
Что изучает планиметрия?
Чтобы подробнее разобраться с тем, что такое планиметрия, следует узнать, что она изучает. Основные фигуры, с которыми имеют дело школьники при освоении базового курса геометрии – это точка, прямая, параллелограмм, окружности, различные многоугольники, треугольники. Они подробно изучают данные фигуры и решают различные геометрические задачи, которые развивают мышление. Конечно, с годами школьная программа меняется, дополняется и корректируется. Но в целом суть остается та же.
Во время учебы школьники знакомятся с понятием параллельности, учатся строить треугольники, четырехугольники. Изучают особенности построения углов, знакомятся с различными теоремами. Узнают многое об окружности и круге, о подобии, начинают первое знакомство с тригонометрическими функциями и еще многое другое. Не стоит пугаться такого объема информации. Лучше отнестись к геометрии как к увлекательному путешествию. Решение геометрических задач – это практически творчество.
Школьникам стоит сразу усвоить, что планиметрия – такой фундамент, который становится подготовкой к более сложным темам. Следующим шагом будет изучение стереометрии, т. е. объемных фигур. И то, насколько хорошо усвоена стереометрия, определит, как легко будет даваться дальнейшее обучение. Чем крепче будет фундамент, тем проще будет по кирпичикам строить новые знания.
Что такое планиметрия кратко
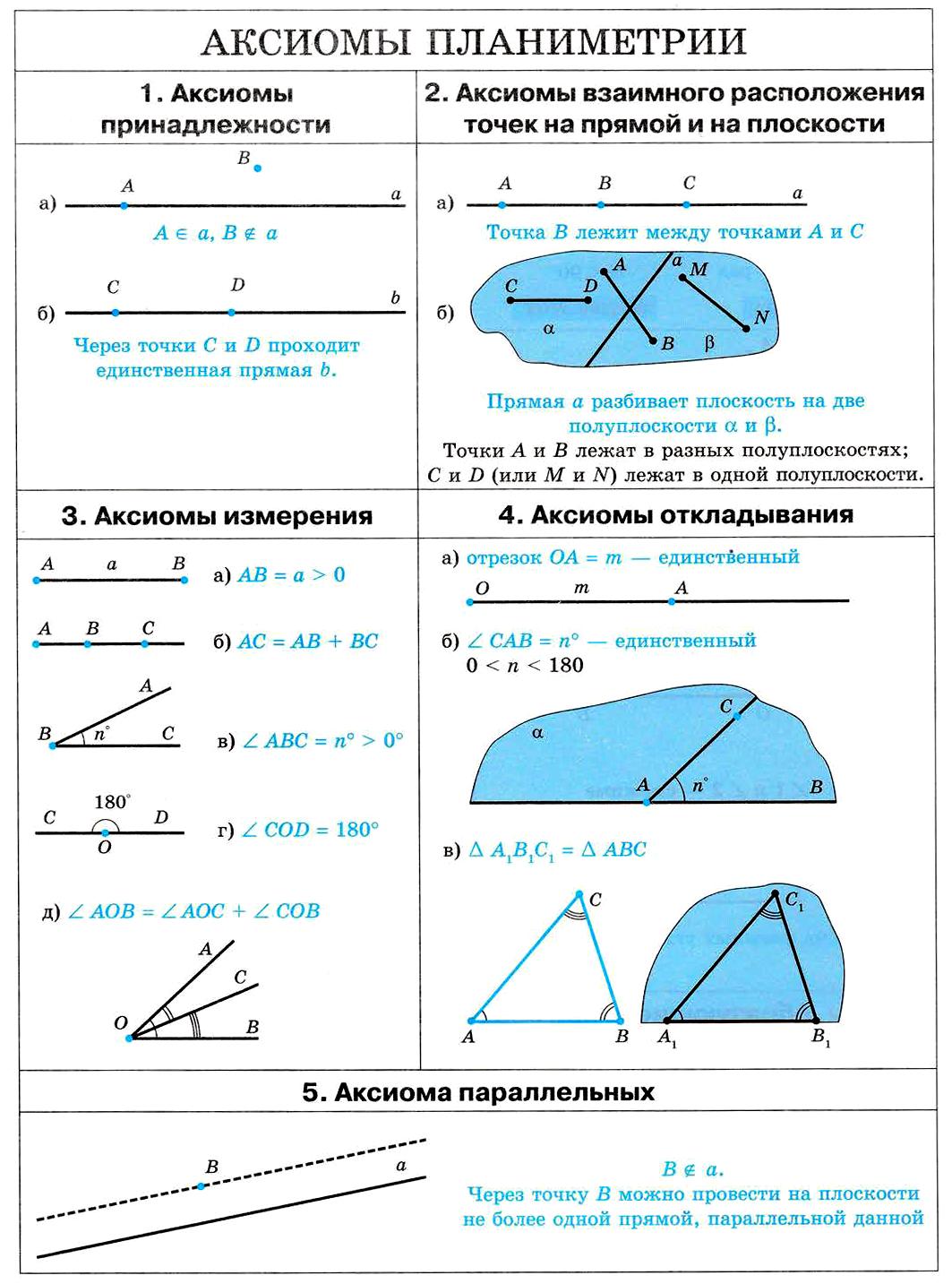
Аксиомы принадлежности. Аксиомы взаимного расположения точек на прямой и плоскости. Аксиомы измерения. Аксиомы откладывания. Аксиома параллельных
02. Углы
Смежные углы. Вертикальные углы. Углы при пересечении
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
04. Свойства сторон и углов треугольника
Свойства сторон и углов треугольника. Внешний угол. Свойства. Неравенство треугольника. Равнобедренный треугольник
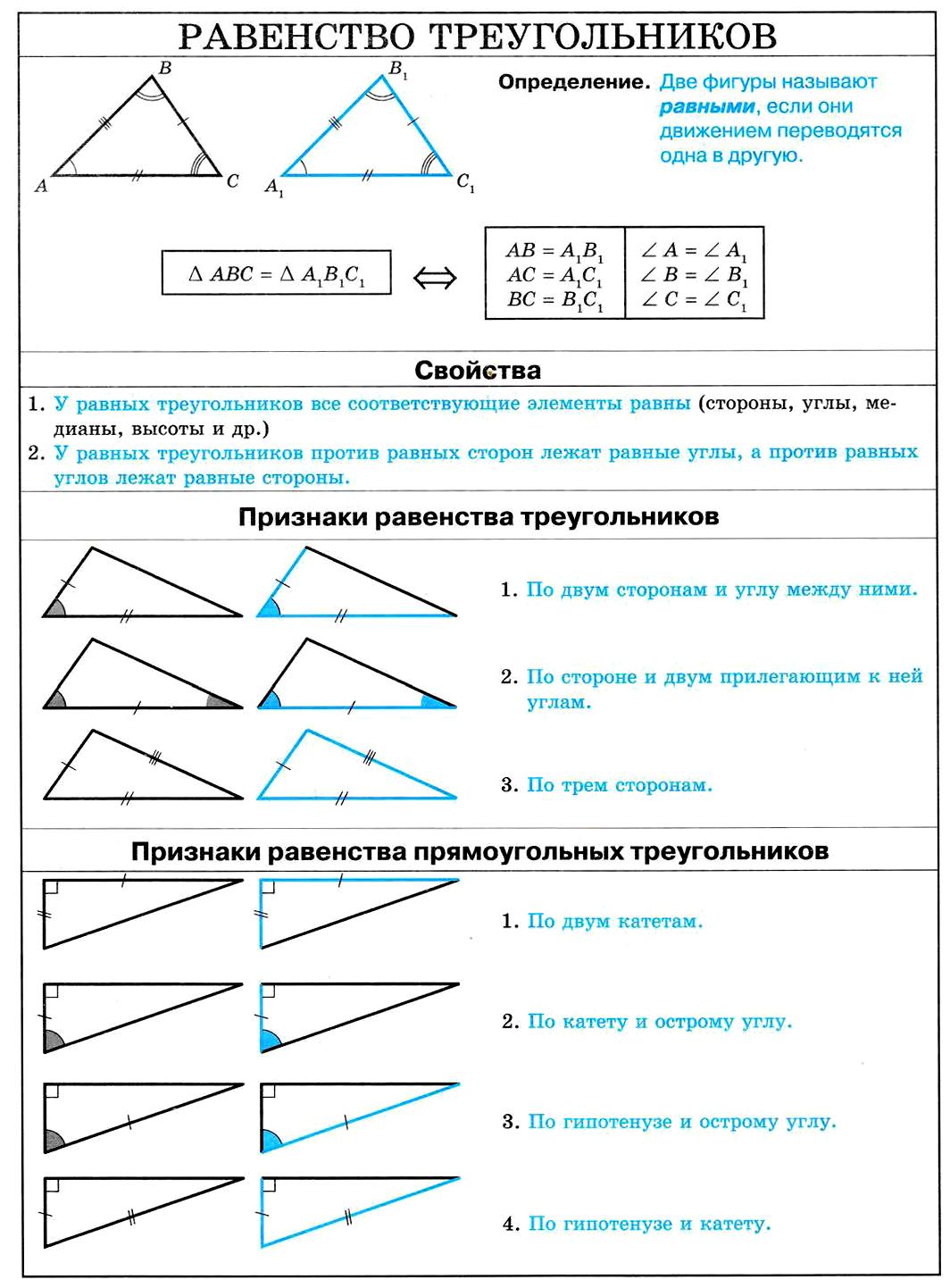
05. Равенство треугольников.
Равенство треугольников. Свойства. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников
06. Медиана треугольника.
Медиана треугольника. Свойства.
07. Биссектриса треугольника.
Биссектриса треугольника. Свойства
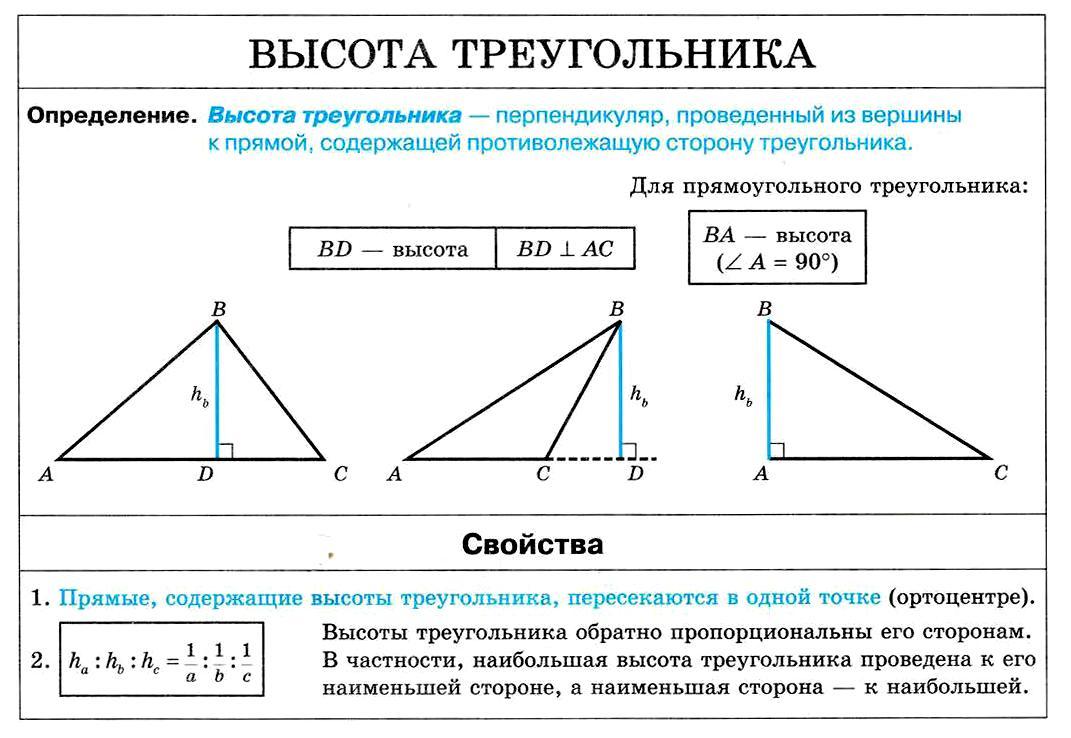
08. Высота треугольника
Высота треугольника. Свойства
09. Средняя линия треугольника
Средняя линия треугольника. Свойства
10. Соотношение между элементами прямоугольного треугольника
Соотношение между элементами прямоугольного треугольника
11. Соотношение между сторонами и углами в произвольном треугольнике
Соотношение между сторонами и углами в произвольном треугольнике
12. Преобразование фигур. Движение
Преобразование фигур. Движение. Симметрия относительно точки. Поворот. Симметрия относительно прямой. Параллельный перенос
13. Преобразование подобия
Преобразование подобия. Свойства. Гомотетия.
14. Подобие треугольников.
Подобие треугольников. Свойства. Признаки подобия треугольников
15. Параллелограмм и его виды.
Параллелограмм и его виды. Свойства. Признаки
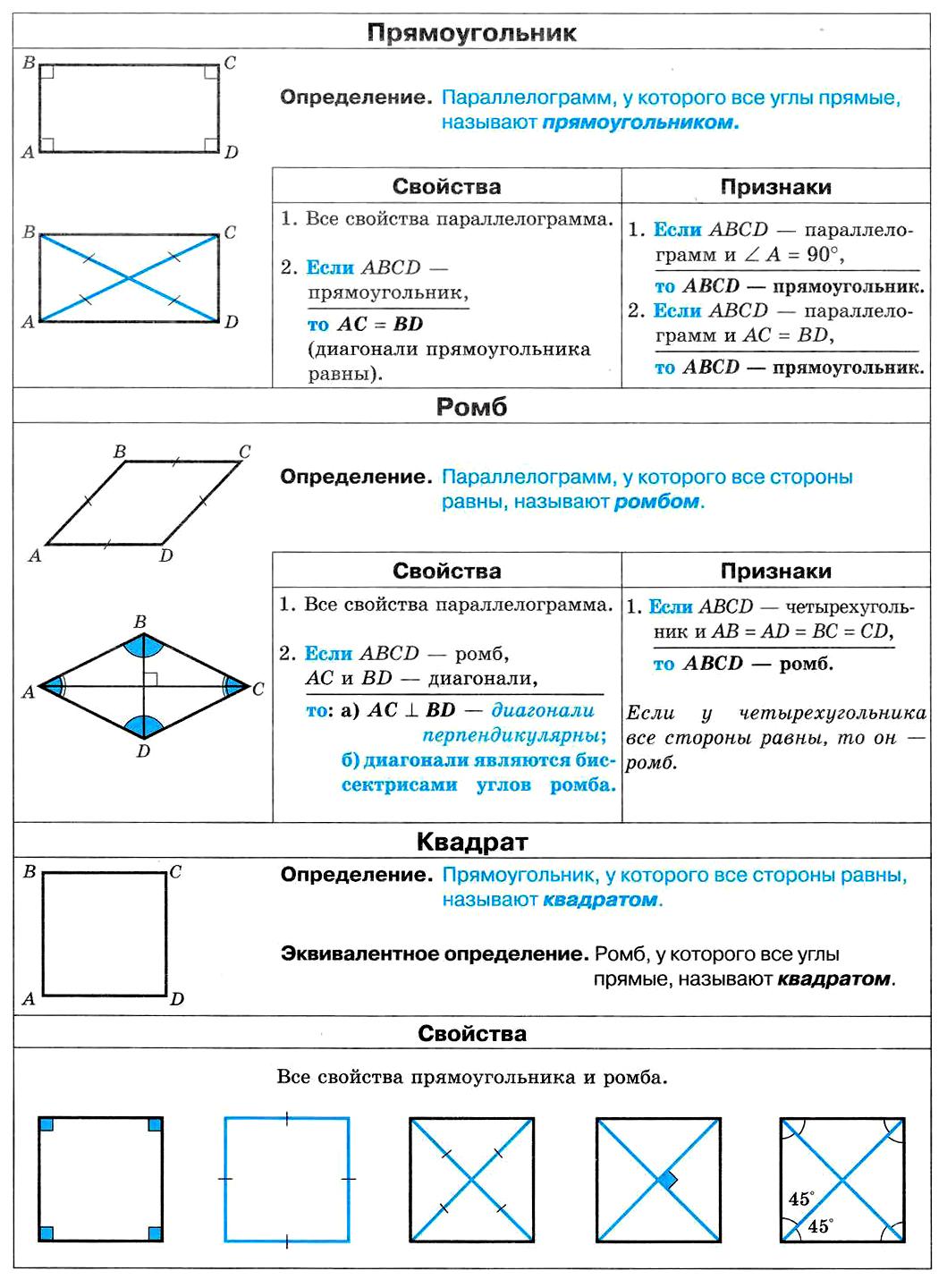
Прямоугольник. Ромб. Квадрат.
16. Трапеция
Трапеция. Частные случаи трапеции. Средняя линия трапеции. Дополнительные построения для трапеции
17. Окружность, хорды и дуги
Окружность, хорды и дуги. Свойства
18. Окружность. Касательные и секущие.
Окружность. Касательные и секущие.
19. Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
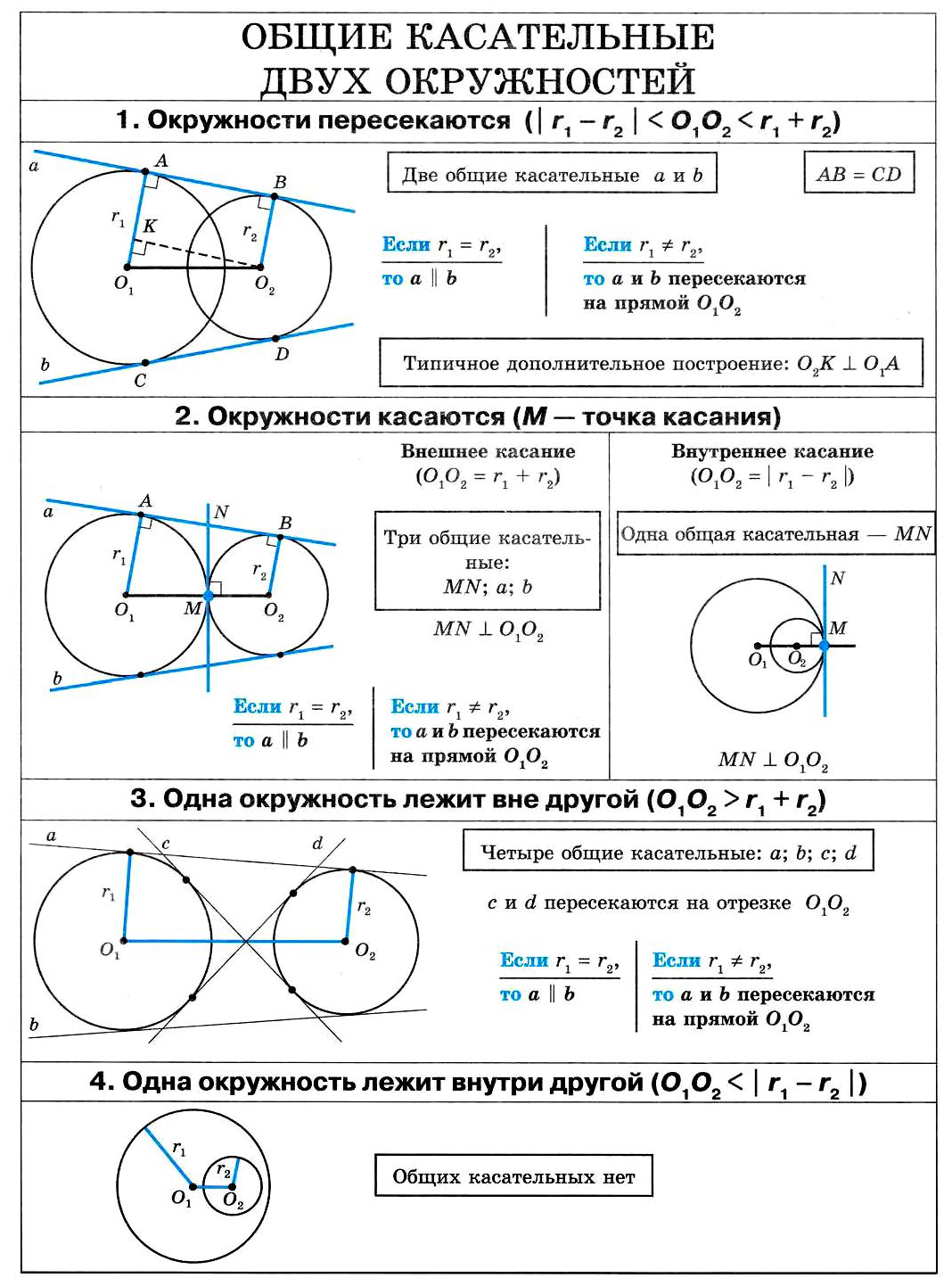
20. Общие касательные двух окружностей.
Общие касательные двух окружностей.
21. Углы в окружности.
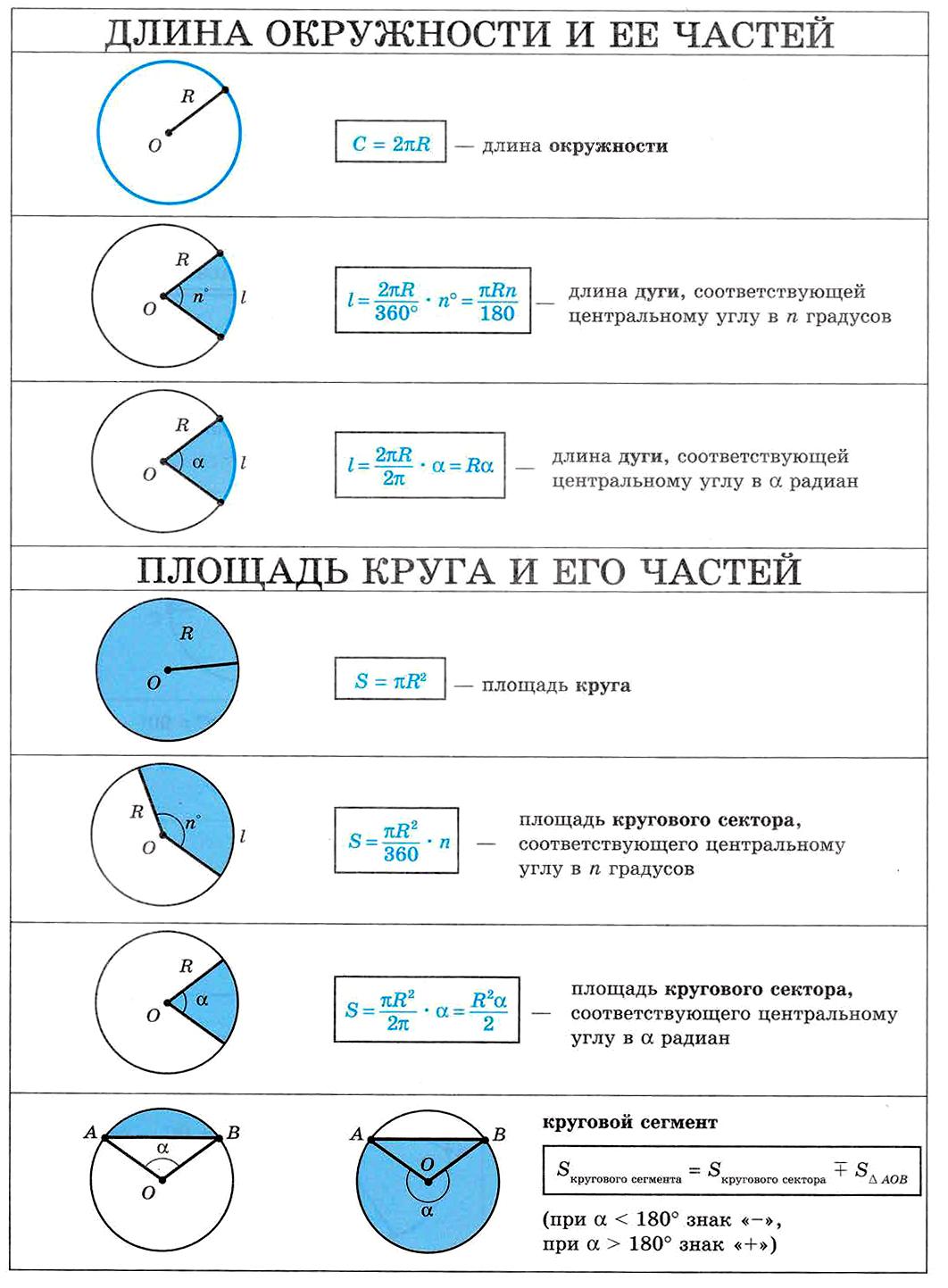
22. Длина окружности и её частей. Площадь круга и его частей
Длина окружности и её частей. Площадь круга и его частей
23. Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
24. Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
25. Окружности, описанные и вписанные в правильные многоугольники
Окружности, описанные и вписанные в правильные многоугольники
26. Площади треугольников.
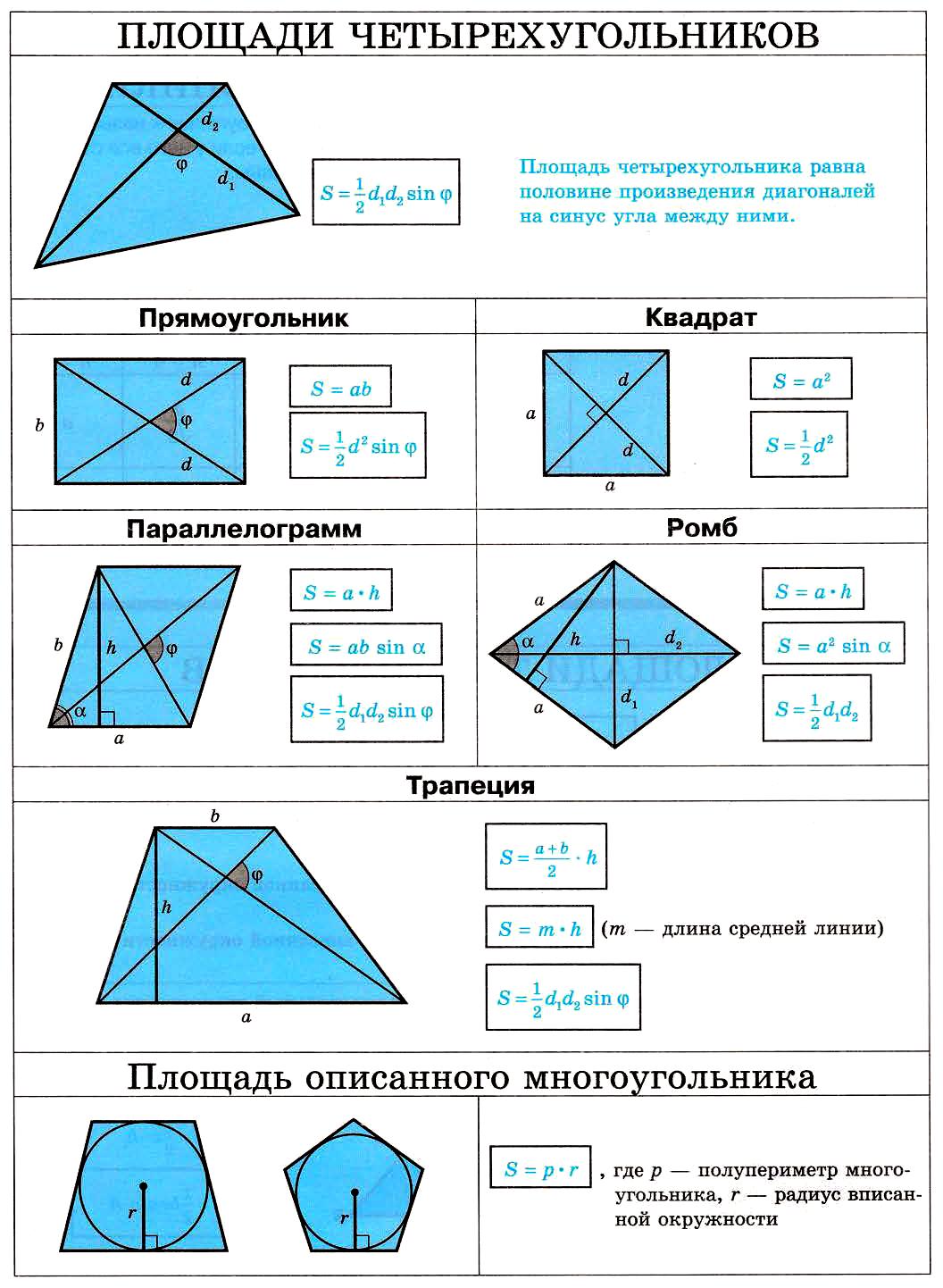
27. Площади четырехугольников.
Площади четырехугольников. Площадь описанного многоугольника
Вы смотрели справочник по геометрии для 7-11 классов «Теоремы и определения по Планиметрии».
2 Комментарии
Огромное спасибо за такую обширную базу по планиметрии. Конечно, сюда можно добавить ещё пару формул, но это самая полная шпаргалка по планиметрии, которую я знаю.
Отличный справочник по планиметрии! Благодарю!
Добавить комментарий Отменить ответ
Конспекты по геометрии:
7 класс
8 класс
9 класс
Найти конспект:
О проекте
Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Возрастная категория: 12+
(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!