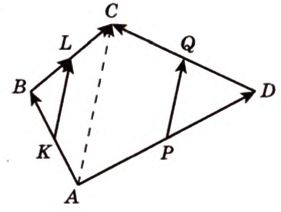
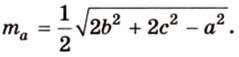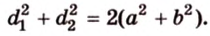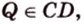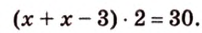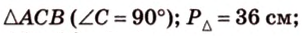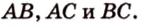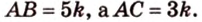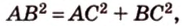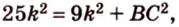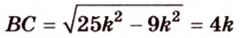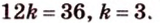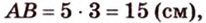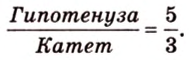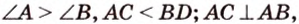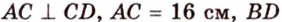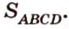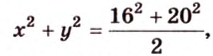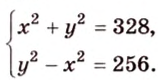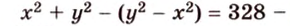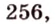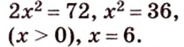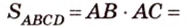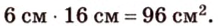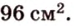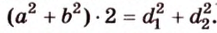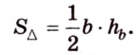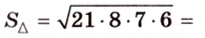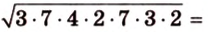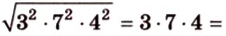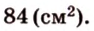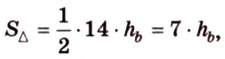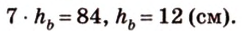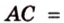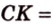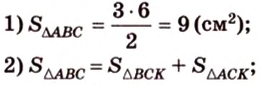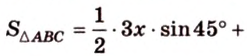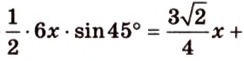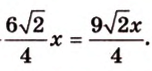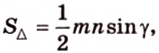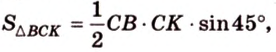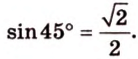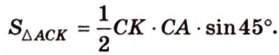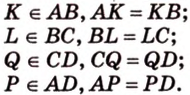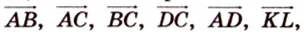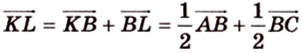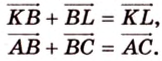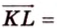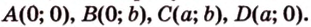Что такое планиметрия в геометрии 7 класс кратко
Планиметрия — основные понятия и аксиомы
Представь, что ты вдруг очутился на другой планете, ну или… в компьютерной игре.
Перед тобой набор неизвестных продуктов, а твоя задача – приготовить из этого набора как можно больше вкусных блюд. Что тебе понадобится?
Конечно же, правила, инструкции – что можно делать с теми или иными продуктами. А то вдруг ты сваришь то, что едят только в сыром виде или, наоборот, положишь в салат то, что непременно нужно варить или жарить? Так что, без инструкций – никуда!
Хорошо, но к чему такое вступление? При чем тут геометрия? Понимаешь, великое множество утверждений о всяких фигурах в геометрии и есть то самое множество «блюд», которые мы должны научиться готовить.
Но из чего? Из основных объектов геометрии! А вот инструкция по их «употреблению» называется умными словами «система аксиом».
Планиметрия — коротко о главном
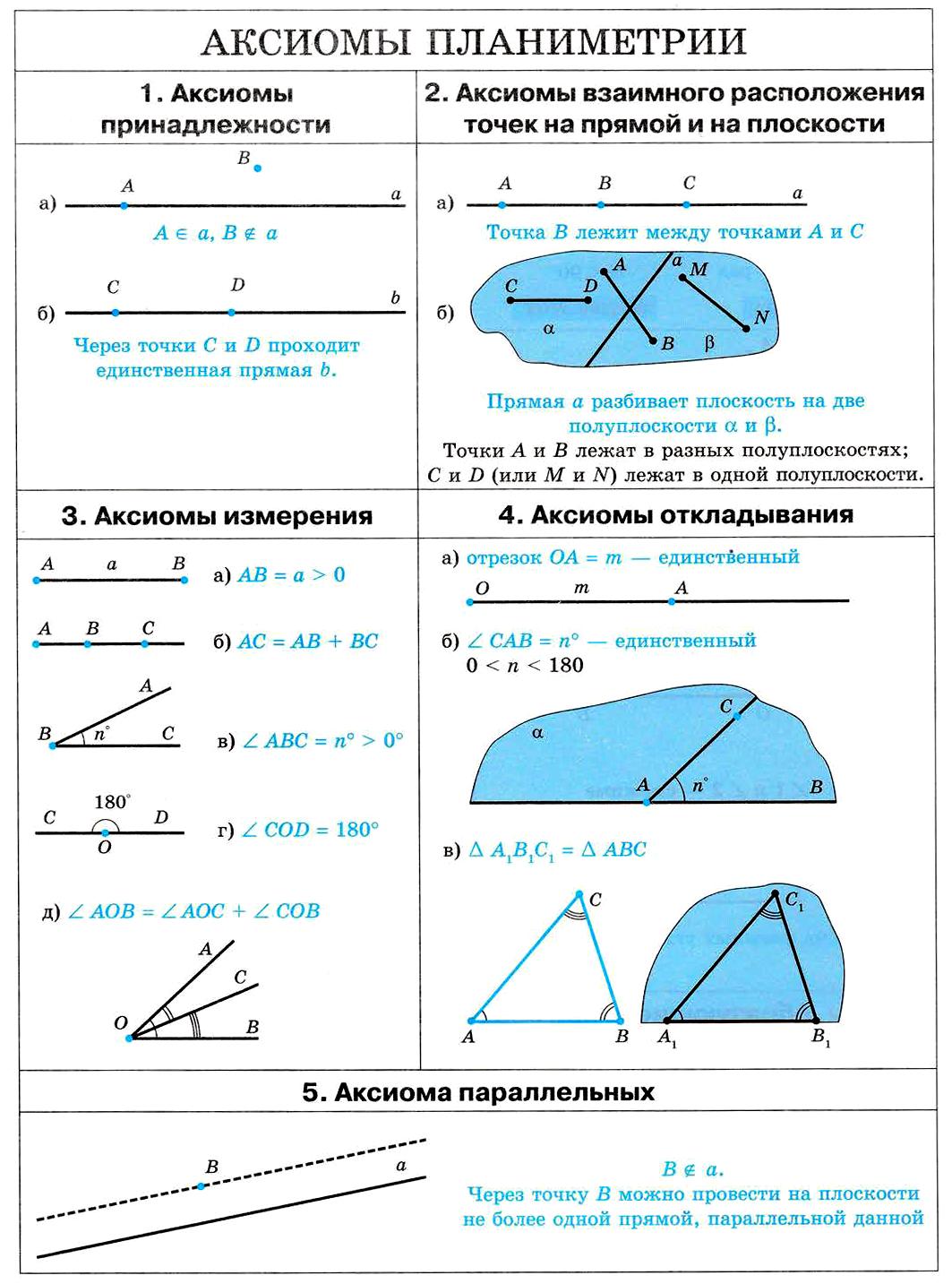
Аксиомы принадлежности:
Аксиомы порядка:
Аксиомы мер для отрезков и углов:
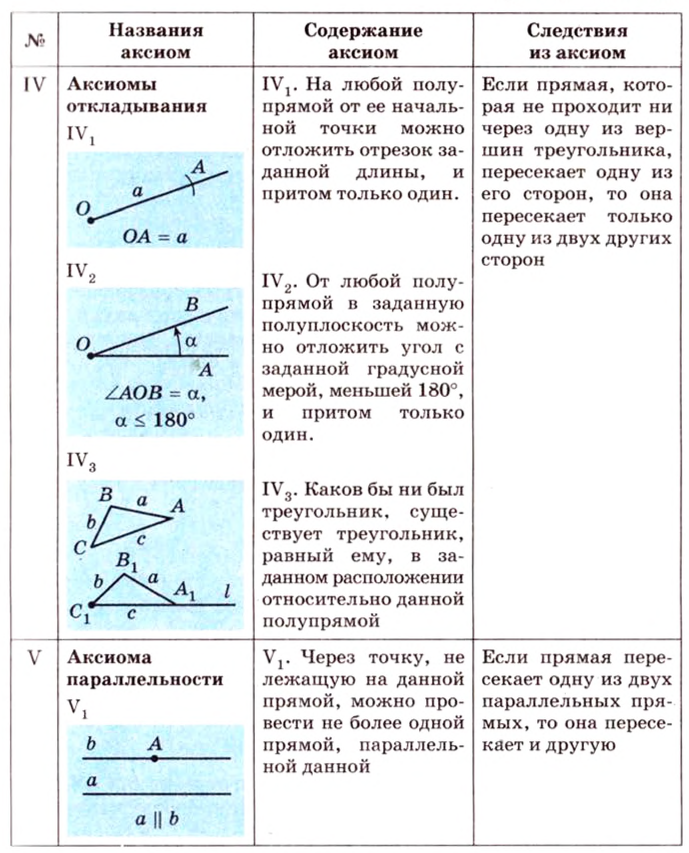
Аксиомы существования треугольника, равного данному:
Следствие 1. От данной точки данной прямой в данную сторону можно отложить отрезок данной длины, причем единственным образом
Следствие 2. От данного луча в данную полуплоскость можно отложить угол данной величины, причем единственным образом
Аксиома параллельных:
Основные факты об углах:
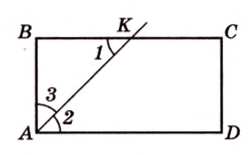
Теорема. Сумма смежных углов равна \( \displaystyle 180<>^\circ \).
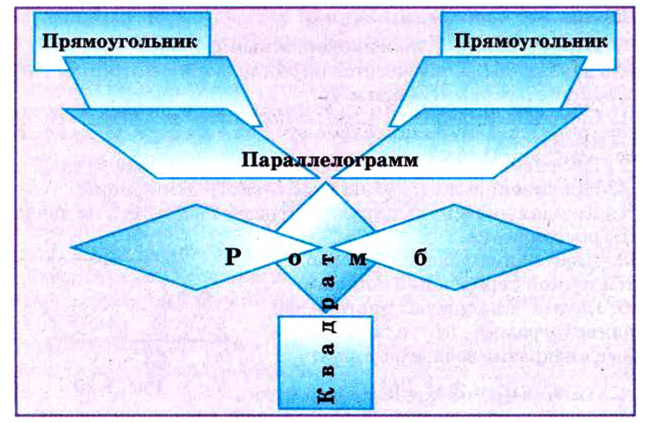
\( \displaystyle 180<>^\circ=x_<1>^<<>^\circ >+x_<2>^<<>^\circ >\)
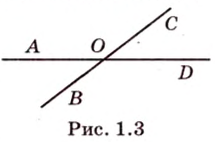
Теорема. Вертикальные углы равны.
\( \displaystyle \angle 1=\angle 2\).
Что такое планиметрия в геометрии 7 класс кратко
Аксиомы принадлежности. Аксиомы взаимного расположения точек на прямой и плоскости. Аксиомы измерения. Аксиомы откладывания. Аксиома параллельных
02. Углы
Смежные углы. Вертикальные углы. Углы при пересечении
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
03. Параллельные прямые. Перпендикулярные прямые. Перпендикуляр к прямой
04. Свойства сторон и углов треугольника
Свойства сторон и углов треугольника. Внешний угол. Свойства. Неравенство треугольника. Равнобедренный треугольник
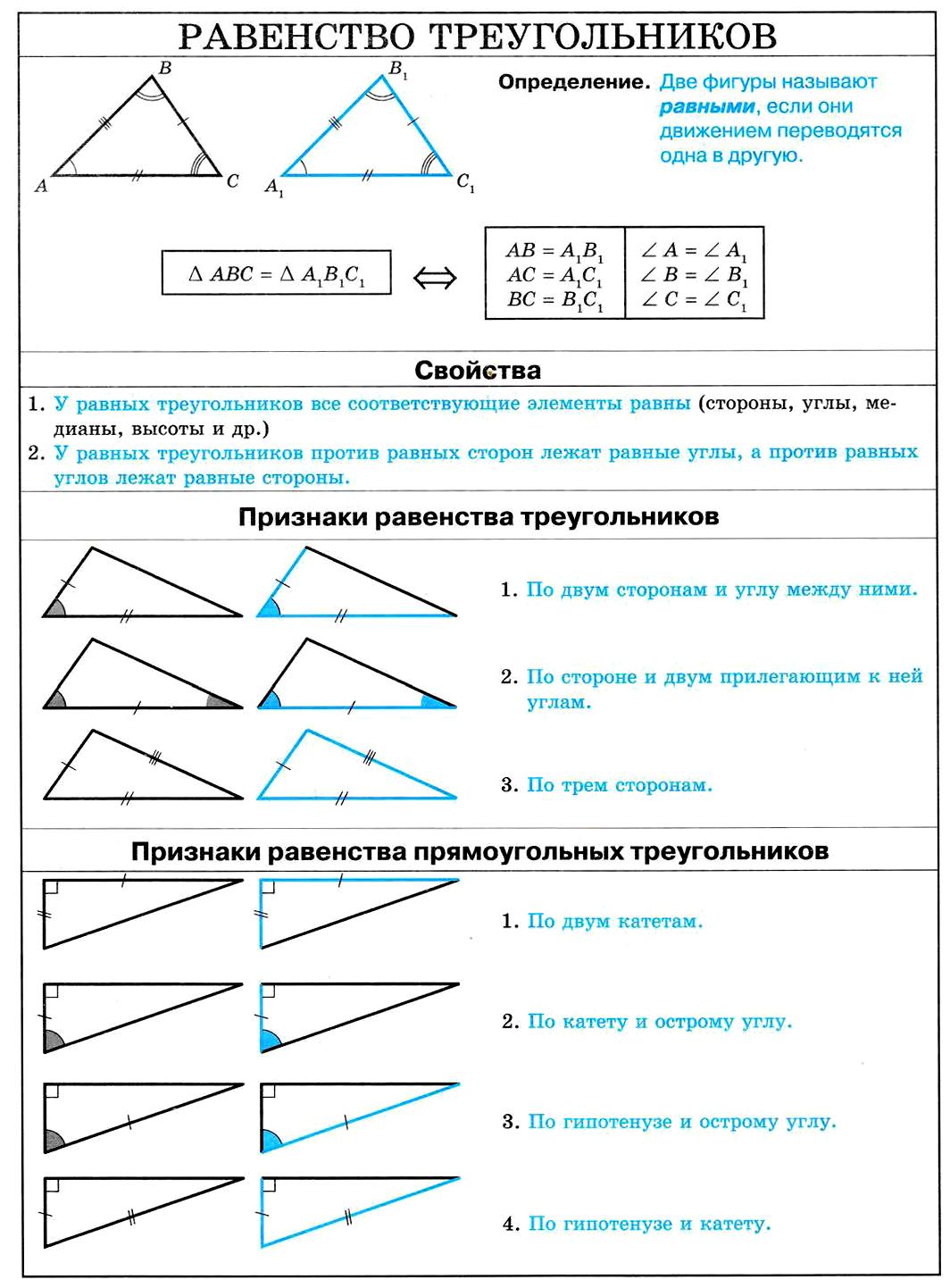
05. Равенство треугольников.
Равенство треугольников. Свойства. Признаки равенства треугольников. Признаки равенства прямоугольных треугольников
06. Медиана треугольника.
Медиана треугольника. Свойства.
07. Биссектриса треугольника.
Биссектриса треугольника. Свойства
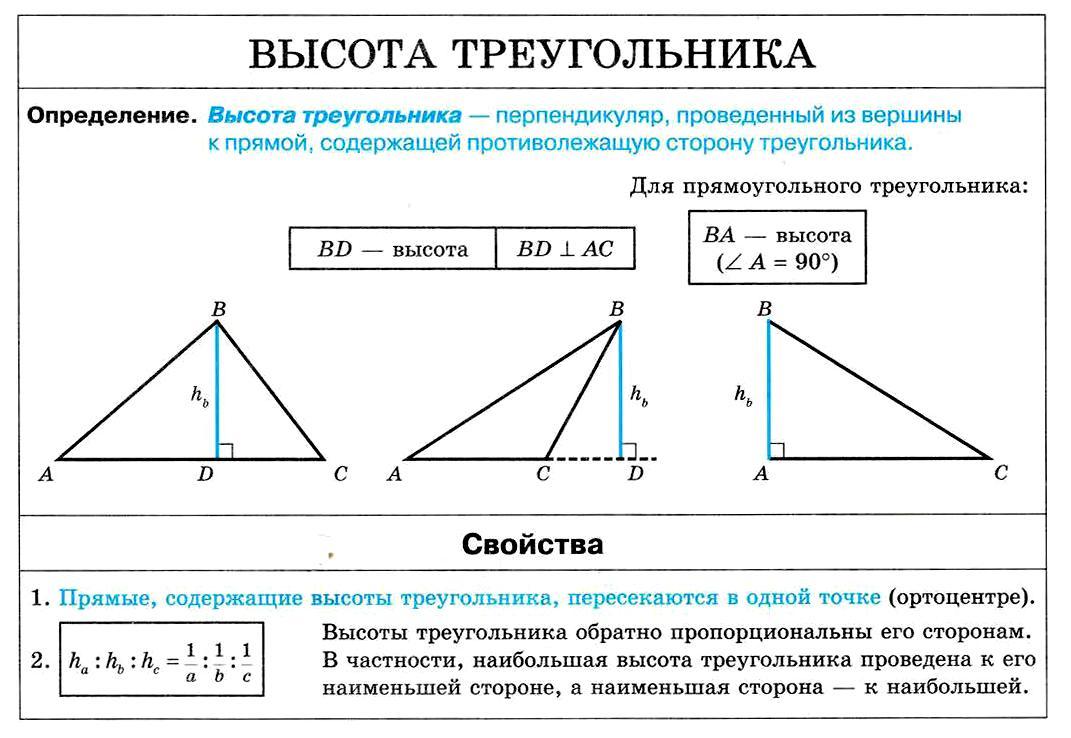
08. Высота треугольника
Высота треугольника. Свойства
09. Средняя линия треугольника
Средняя линия треугольника. Свойства
10. Соотношение между элементами прямоугольного треугольника
Соотношение между элементами прямоугольного треугольника
11. Соотношение между сторонами и углами в произвольном треугольнике
Соотношение между сторонами и углами в произвольном треугольнике
12. Преобразование фигур. Движение
Преобразование фигур. Движение. Симметрия относительно точки. Поворот. Симметрия относительно прямой. Параллельный перенос
13. Преобразование подобия
Преобразование подобия. Свойства. Гомотетия.
14. Подобие треугольников.
Подобие треугольников. Свойства. Признаки подобия треугольников
15. Параллелограмм и его виды.
Параллелограмм и его виды. Свойства. Признаки
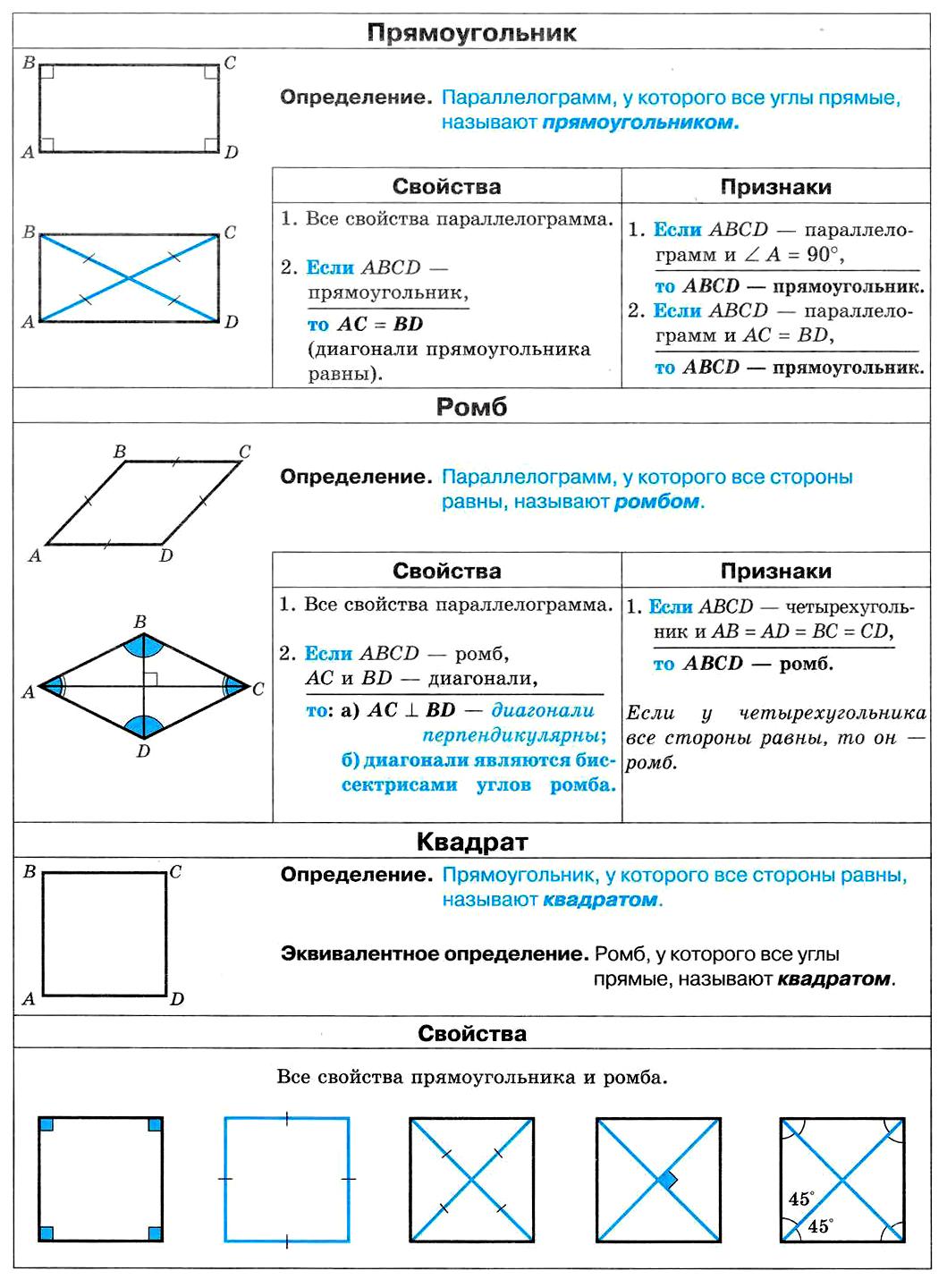
Прямоугольник. Ромб. Квадрат.
16. Трапеция
Трапеция. Частные случаи трапеции. Средняя линия трапеции. Дополнительные построения для трапеции
17. Окружность, хорды и дуги
Окружность, хорды и дуги. Свойства
18. Окружность. Касательные и секущие.
Окружность. Касательные и секущие.
19. Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
Взаимное расположение прямой и окружности. Взаимное расположение двух окружностей.
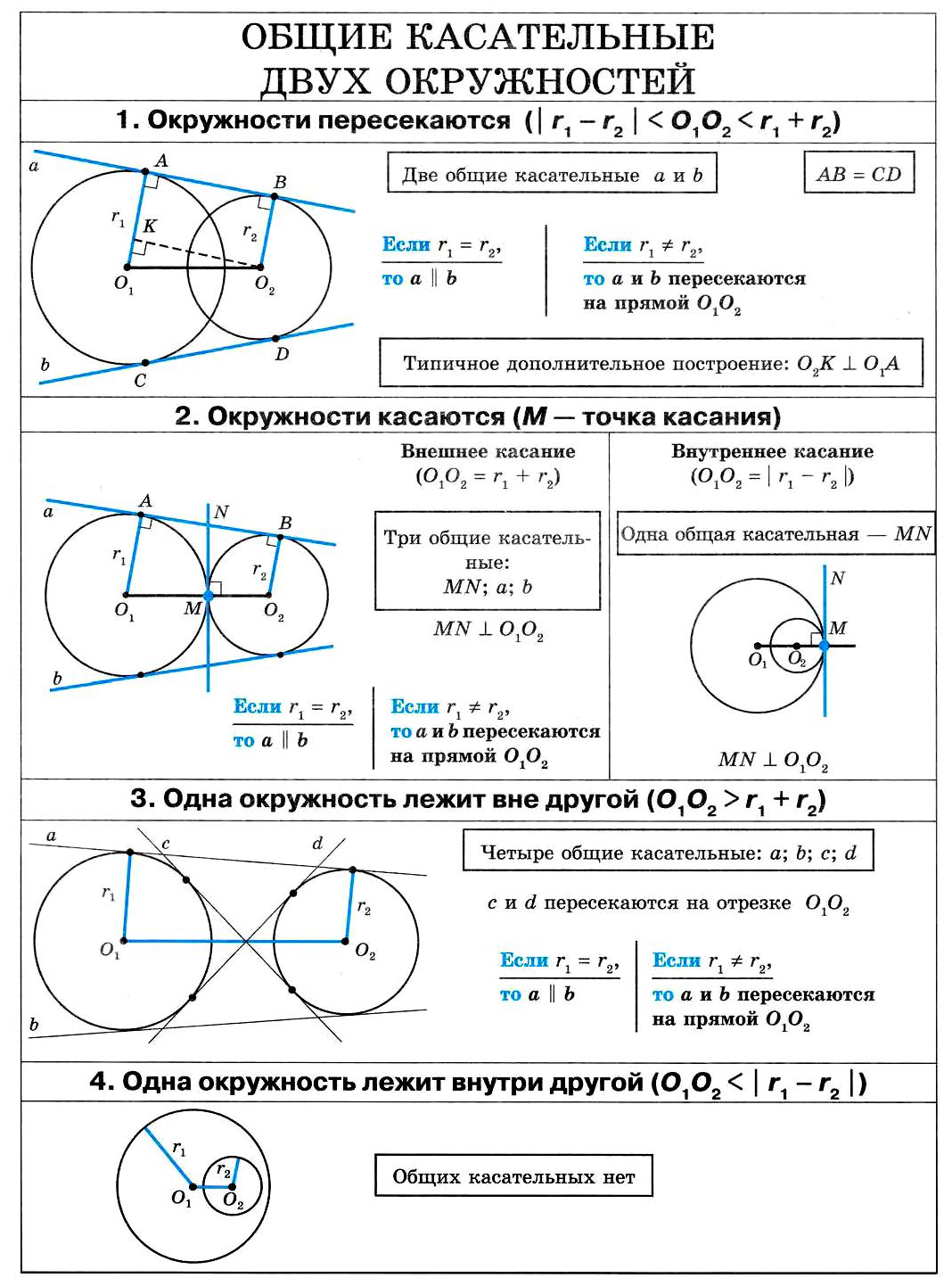
20. Общие касательные двух окружностей.
Общие касательные двух окружностей.
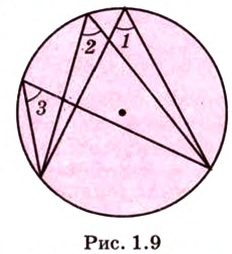
21. Углы в окружности.
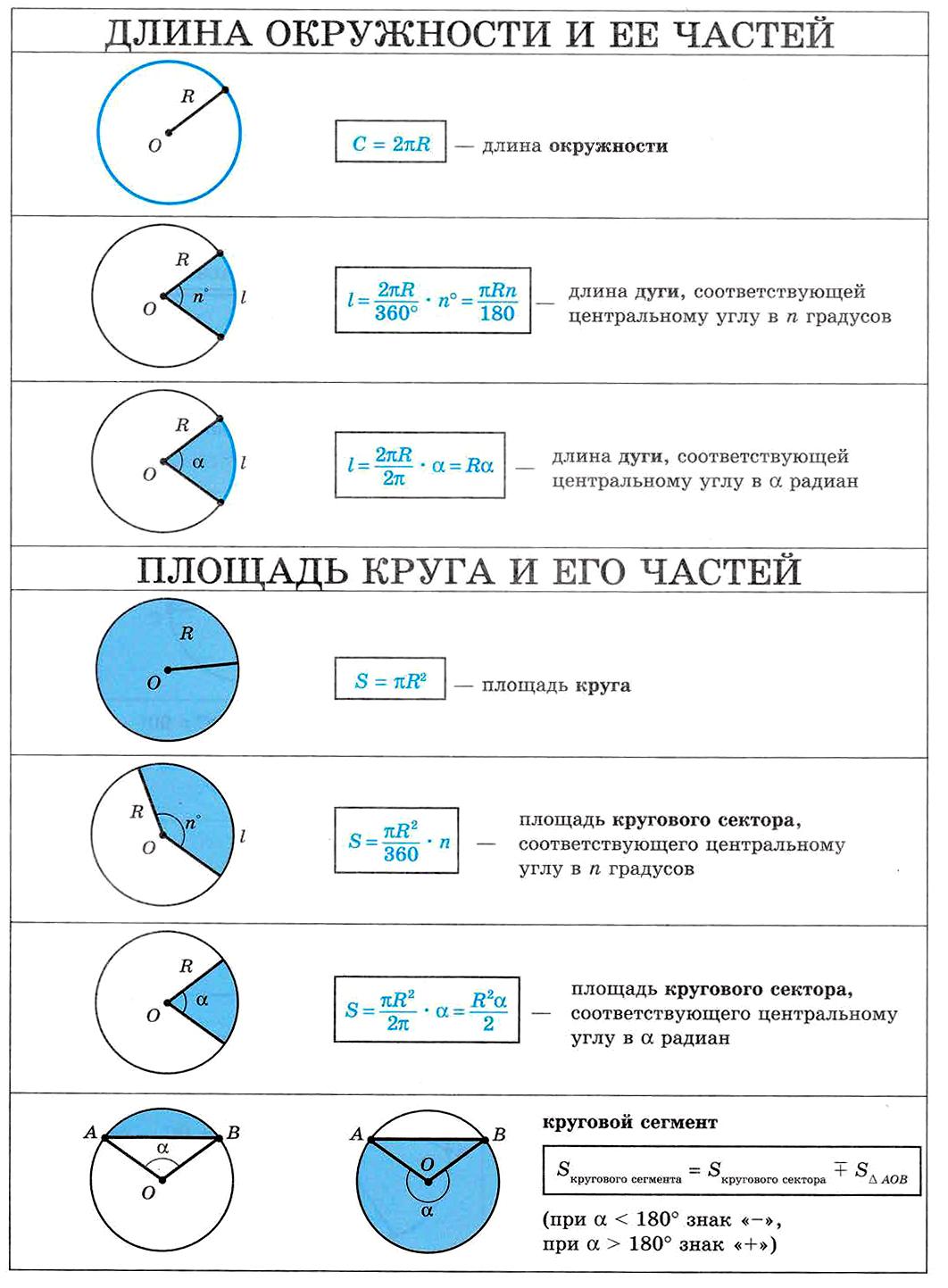
22. Длина окружности и её частей. Площадь круга и его частей
Длина окружности и её частей. Площадь круга и его частей
23. Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
Вписанный и описанный многоугольники. Вписанный и описанный четырехугольники. Прямоугольник. Трапеция и ромб. Квадрат.
24. Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
Окружность, описанная около треугольника, и окружность, вписанная в треугольник.
25. Окружности, описанные и вписанные в правильные многоугольники
Окружности, описанные и вписанные в правильные многоугольники
26. Площади треугольников.
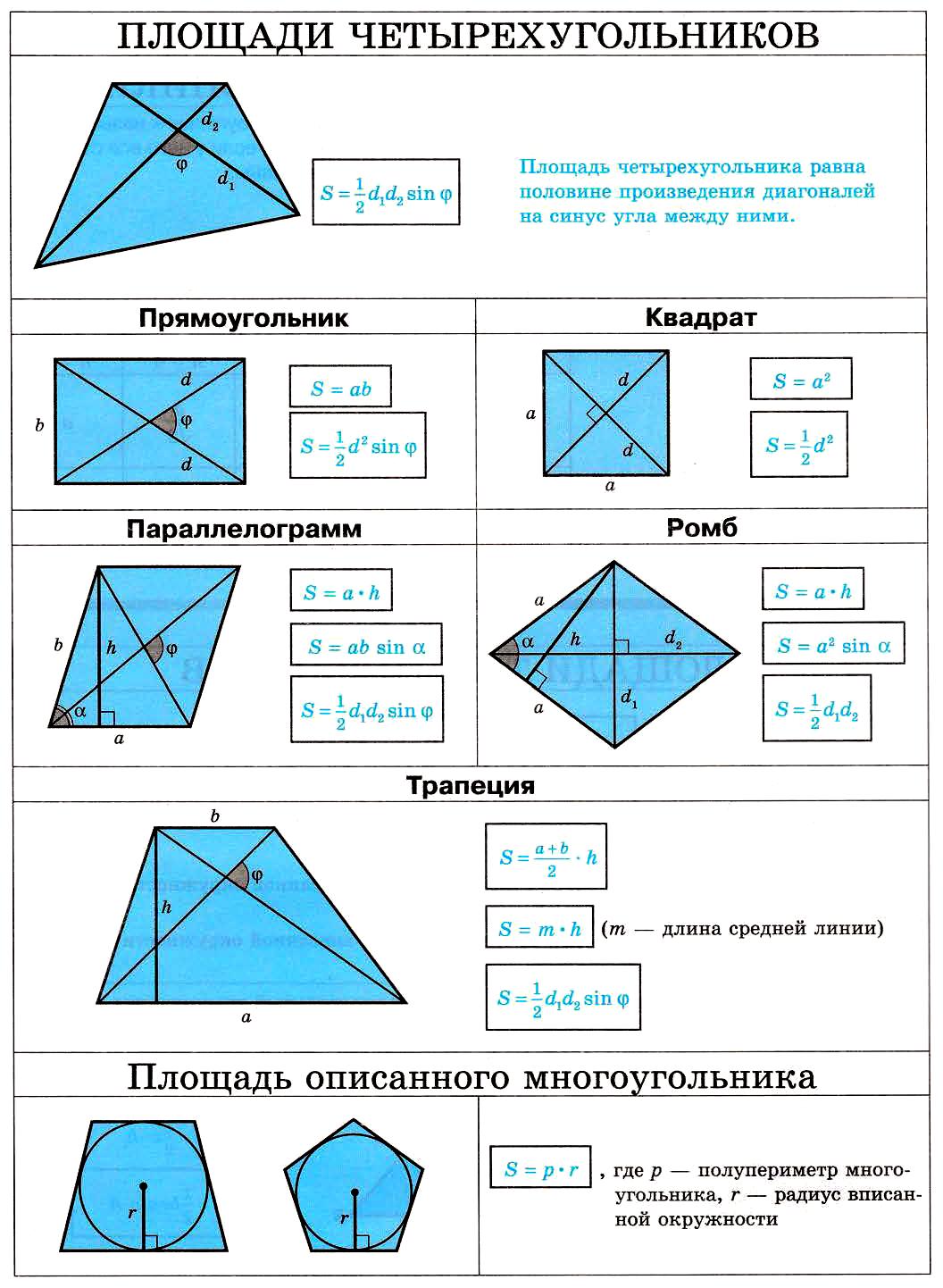
27. Площади четырехугольников.
Площади четырехугольников. Площадь описанного многоугольника
Вы смотрели справочник по геометрии для 7-11 классов «Теоремы и определения по Планиметрии».
2 Комментарии
Огромное спасибо за такую обширную базу по планиметрии. Конечно, сюда можно добавить ещё пару формул, но это самая полная шпаргалка по планиметрии, которую я знаю.
Отличный справочник по планиметрии! Благодарю!
Добавить комментарий Отменить ответ
Конспекты по геометрии:
7 класс
8 класс
9 класс
Найти конспект:
О проекте
Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.
Возрастная категория: 12+
(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!
Что такое планиметрия? знакомство с геометрией
Об аксиомах планиметрии
Что такое планиметрия? Определение в геометрии
Планиметрия – это раздел геометрии, изучающий фигуры, которые можно расположить в пределах одной плоскости. Например, квадрат, начерченный на листке бумаги, будет относиться к планиметрии.
Планиметрия – это первый шаг школьников к близкому знакомству с геометрией. Именно в планиметрии они узнают о существовании таких понятий, как отрезок, прямая, точка, направление, плоскость и т. д. Для дальнейшего движения в освоении геометрии школьники усваивают, что такое планиметрия. Для них это основа основ. Происходит первое знакомство с теоремами, аксиомами, новыми терминами, явлениями.
Аксиомы и теоремы
Подробнее разберемся с аксиомами. В планиметрии это наиважнейшие правила, по которым работает вся наука. Да и не только в ней. По определению, речь идет об утверждениях, не требующих доказательств.
Аксиомы, которые буду рассмотрены ниже, входят в так называемую Евклидовую геометрию.
Это 2 утверждения принято называть аксиомами принадлежности, а следующие – порядка:
На плоскости расположена прямая. Через любую точку, не принадлежащую ей, можно провести лишь одну прямую, параллельную данной.








Теоремы в планиметрии — это уже не совсем фундаментальные утверждения. Обычно их принимают как факт, но каждая из них имеет доказательство, построенное на основных понятиях, упомянутых выше. Кроме того, их очень много. Разобрать все будет довольно трудно, но в представленном материале будут присутствовать некоторые из них.
Со следующими двумя стоит ознакомиться пораньше:
Эти две теоремы могут пригодиться в решении геометрических задач, связанных с n-угольниками. Они довольно просты и интуитивно понятны. Стоит их запомнить.
Происхождение слова
Как и многие другие термины, слово «планиметрия» берет свое начало в латинском языке. В переводе оно означает «плоскость», «измеряю». Еще древнегреческие философы ввели его в употребление и дали ему определение. Что такое планиметрия, сейчас знает каждый школьник, ведь с нее начинается изучение геометрии.
Планиметрию относят к Евклидовой геометрии или, как ее еще называют, элементарной геометрии. Евклид – древнегреческий философ, а его главный труд – «Начало» – считается вершиной античной математики. Работы этого философа определили ход развития математики и были предметом изучения и обсуждений в течение очень многих лет.








Что изучает планиметрия?
Чтобы подробнее разобраться с тем, что такое планиметрия, следует узнать, что она изучает. Основные фигуры, с которыми имеют дело школьники при освоении базового курса геометрии – это точка, прямая, параллелограмм, окружности, различные многоугольники, треугольники. Они подробно изучают данные фигуры и решают различные геометрические задачи, которые развивают мышление. Конечно, с годами школьная программа меняется, дополняется и корректируется. Но в целом суть остается та же.
Во время учебы школьники знакомятся с понятием параллельности, учатся строить треугольники, четырехугольники. Изучают особенности построения углов, знакомятся с различными теоремами. Узнают многое об окружности и круге, о подобии, начинают первое знакомство с тригонометрическими функциями и еще многое другое. Не стоит пугаться такого объема информации. Лучше отнестись к геометрии как к увлекательному путешествию. Решение геометрических задач – это практически творчество.
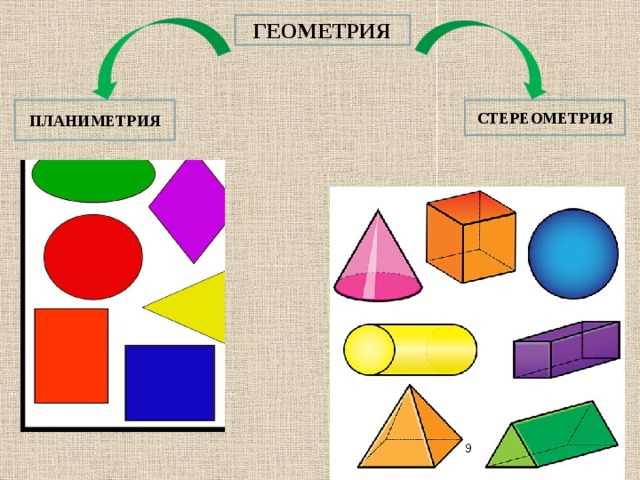
Школьникам стоит сразу усвоить, что планиметрия – такой фундамент, который становится подготовкой к более сложным темам. Следующим шагом будет изучение стереометрии, т. е. объемных фигур. И то, насколько хорошо усвоена стереометрия, определит, как легко будет даваться дальнейшее обучение. Чем крепче будет фундамент, тем проще будет по кирпичикам строить новые знания.
Планиметрия
Планиметрия (от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости.
Первое систематическое изложение планиметрии впервые было дано Евклидом в его труде «Начала».
Содержание
Изучение в школьном курсе
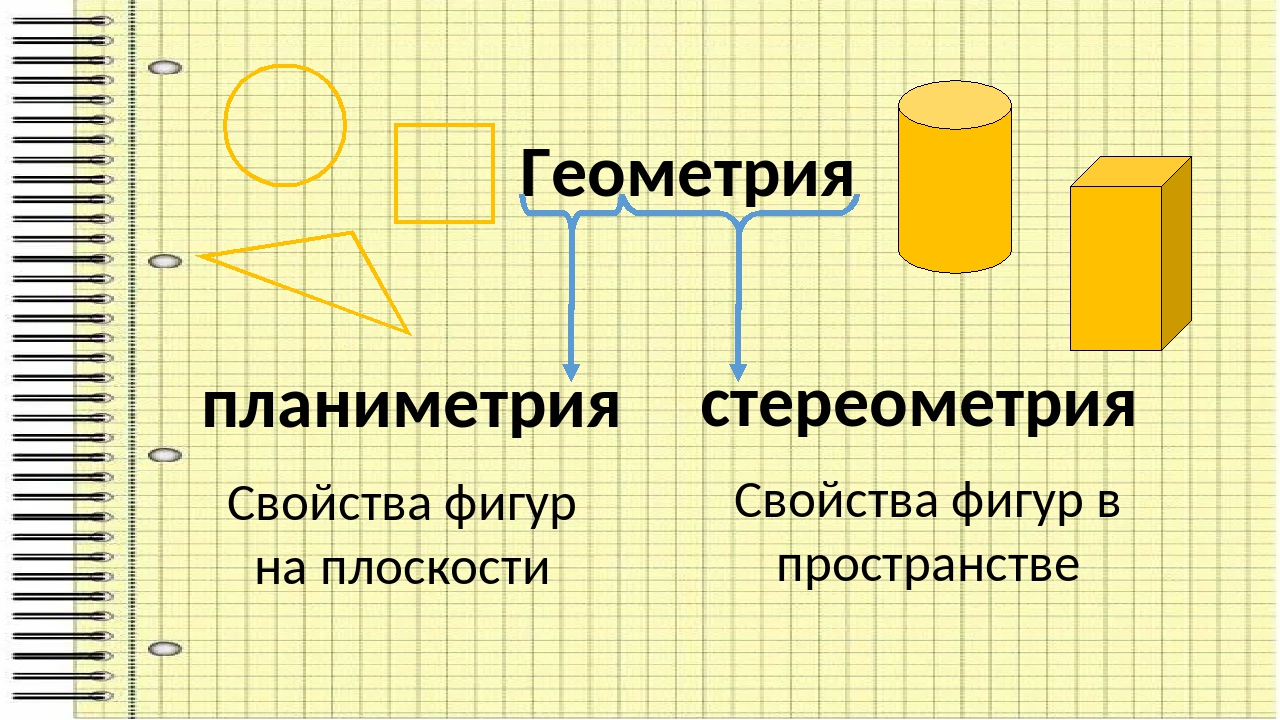
При систематическом изучении школьного курса геометрии обычно начинают с изучения планиметрии, а затем приступают к изучению стереометрии, изучающей пространственные фигуры. Основными понятиями школьного курса планиметрии являются точка, прямая, плоскость и расстояние (между двумя точками или от точки до точки), а также некоторые общематематические понятия, такие, как множество, отображение множества на множество и некоторые другие.
Содержание школьного курса из года в год несколько меняется, однако его ядро остаётся в целом неизменным. Планиметрия содержит:
Были попытки излагать обе части геометрии (планиметрию и стереометрию) вместе, слитно, изучая плоские и пространственные фигуры одновременно.
Фигуры, изучаемые планиметрией
См. также
Ссылки
Литература
Задачники
| Геометрия | Алгебраическая геометрия • Аналитическая геометрия • Евклидова геометрия • Неевклидова геометрия • Планиметрия • Стереометрия • Тригонометрия |
|---|---|
| Топология | Общая топология • Алгебраическая топология |
| Смежные направления | Дифференциальная геометрия и топология • Геометрическая топология |
Полезное
Смотреть что такое «Планиметрия» в других словарях:
планиметрия — планиметрия … Орфографический словарь-справочник
ПЛАНИМЕТРИЯ — (от лат. planus плоский, и греч. metreo меряю). Часть геометрии, занимающаяся исследованием и измерением фигур на плоскости. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПЛАНИМЕТРИЯ от лат. planus, плоский, и… … Словарь иностранных слов русского языка
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, планировать и пр. см. план. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, подраздел ГЕОМЕТРИИ, в которой линии, углы и фигуры представлены в двухмерной форме, т.е. на плоскости. В планиметрии действуют аксиомы ЕВКЛИДА … Научно-технический энциклопедический словарь
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, планиметрии, мн. нет, жен. (от лат. planum плоскость и греч. metreo мерю) (мат.). Отдел элементарной геометрии, изучающий фигуры на плоскости. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, и, жен. Часть геометрии, изучающая фигуры на плоскости. | прил. планиметрический, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
планиметрия — сущ., кол во синонимов: 2 • геометрия (9) • математика (29) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
ПЛАНИМЕТРИЯ — ПЛАНИМЕТРИЯ, измерение площадей плоскостных фигур, очень часто применяемое в мед. физиол. исследовательских работах, преиму i щественно по отношению к площадям кривых, записанных на кимографе. Такое измерение можно производить или с помощью… … Большая медицинская энциклопедия
Содержание:
Что такое планиметрия
Логическое построение планиметрии можно описать как последовательность следующих этапов.
Для школьного курса планиметрии определены:
К определяемым понятиям в геометрии относят отрезок, луч, треугольник и т. п., поскольку для них существуют объяснения «что это такое?». Определяемых понятий много. Приведем пример.
Аксиомы планиметрии
С целью установления правильности утверждения о свойствах той или иной геометрической фигуры прибегают к некоторым рассуждениям. Среди них есть такие, которые требуют доказательства (теоремы, задачи). Утверждение, истинность которого устанавливается путем доказательства и которое используется для доказательства других утверждений, называют теоремой.
Теорема состоит из: условия и вывода. Для доказательства теорем в школьном курсе геометрии в основном используют следующие методы:
Все рассуждения при доказательстве теорем произвольным методом основываются на аксиомах и известных доказанных фактах. Т.е. чтобы доказать теорему, разрешается пользоваться только основными свойствами простейших фигур (аксиомами) и свойствами, доказанными ранее (теоремами). Никакими другими свойствами фигур, даже если они представляются очевидными, пользоваться нельзя. Например, доказывая теоремы, можно использовать рисунки. Однако это лишь геометрическая модель содержания текста, выраженного словами, поэтому делать по рисунку выводы о свойствах фигур не разрешается.
Итак, геометрия, как и другие математические науки, строится по такой схеме: сначала следует ввести основные понятия, задать аксиомы (правила игры), а потом, опираясь на аксиомы, выводить другие факты (проводить игру по определенным правилам, не противоречащим друг другу).
Опорные факты курса планиметрии
Данный параграф предназначен для повторения курса планиметрии. Необходимость в нем обусловлена тем, что многие вопросы планиметрии на первом этапе обучения в школе рассматриваются несколько поверхностно. В следующих классах уровень изучения материала повышается, а вернуться и углубить пройденное удается не всегда. Поэтому мы систематизируем и обобщим основные сведения по планиметрии, условно разбив их на блоки: взаимное расположение прямых на плоскости; окружность и круг; многоугольники; треугольник и его элементы; выпуклые четырехугольники.
Взаимное расположение прямых на плоскости
Расстоянием от точки 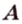
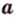
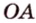
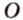
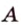
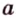
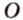
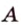
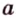
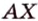
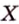
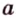
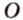
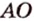
Две различные прямые 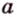
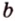
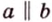
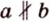
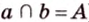
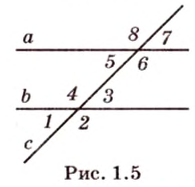
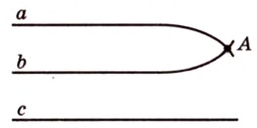
Вследствие пересечения двух прямых третьей прямой образуется восемь углов (рис. 1.5) (прямые а и Ь могут пересекаться, но прямая с через точку их пересечения не проходит):
Признаки параллельности прямых:
Окружность и круг
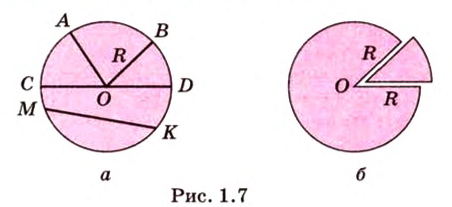
Кругом с центром 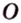
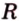
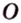
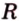
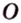
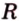
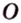
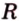
Отрезки, которые соединяют центр с точками окружности и имеют длину 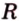
Части круга, на которые он делится двумя радиусами, называют круговыми секторами (рис. 1.7, б).
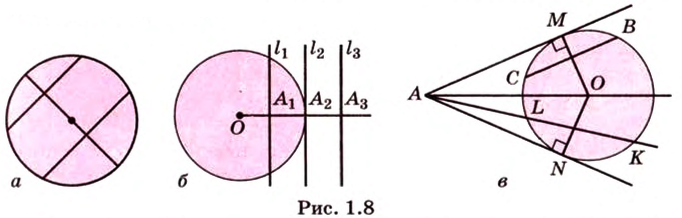
Через три точки, не лежащие на одной прямой, проходит единственная окружность. Диаметр, перпендикулярный к хорде, делит пополам эту хорду и обе дуги, которые стягиваются ею, и наоборот, если диаметр проведен через середину хорды, то он перпендикулярен этой хорде и делит пополам дугу, которую она стягивает (рис. 1.8, а).
Дуги, которые находятся между параллельными хордами, равны между собой. Равные дуги стягиваются равными хордами, и наоборот, равные хорды стягивают равные дуги.
Равные хорды одинаково отдалены от центра, и наоборот, хорды, одинаково отдаленные от центра, равны между собой. Большая из двух хорд меньше отдалена от центра, и наоборот, из двух хорд больше та, которая меньше отдалена от центра (рис. 1.8, а).
Каким может быть взаимное расположение прямой и окружности?
Рассмотрим окружность с центром 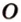
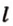
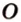
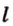
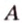
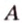
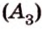
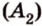
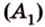
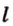
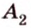
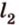
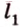
Прямая, проходящая через точку окружности, является касательной к окружности только тогда, когда она перпендикулярна радиусу, проведенному в эту точку. Если касательная параллельна хорде окружности, то точка касания делит пополам дугу, которую стягивает хорда (рис. 1.8, в; 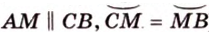
Если из одной точки к окружности проведены две касательные, то отрезки этих касательных (от точек касания до данной точки) равны между собой, а луч, проведенный через данную точку и центр окружности, делит пополам угол между касательными (рис. 1.8, в; 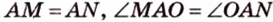
Угол, образованный двумя касательными, называется описанным (рис. 1.8, в; 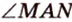
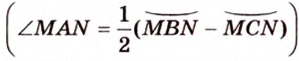
Многоугольники
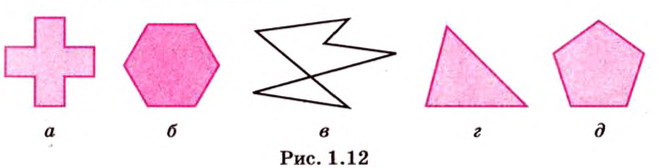
Многоугольник выпуклый, если он лежит в одной полуплоскости относительно каждой прямой, проходящей через две его соседние вершины (рис. 1.12, б, г, д).
Многоугольники называют равными, если при наложении они совмещаются. Для выпуклого 
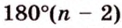

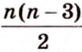

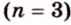
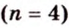
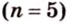
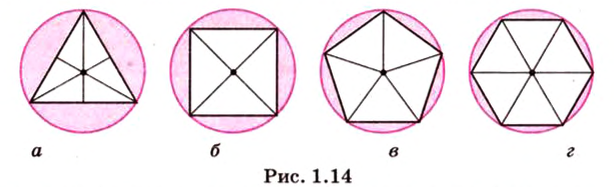
Как построить правильный 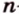
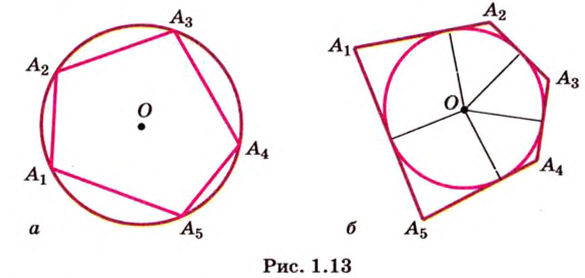
Если окружность разделить на 

Если окружность разделить на 

Вокруг каждого правильного многоугольника можно описать окружность или в каждый правильный многоугольник можно вписать окружность.
В правильном многоугольнике центры описанной и вписанной окружностей совпадают. Общий центр описанной и вписанной окружностей называется центром правильного многоугольника. Радиус вписанной окружности называют апофемой правильного многоугольника.
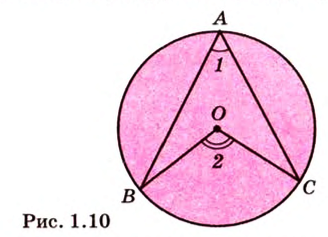
Угол, образованный двумя радиусами, проведенными через смежные вершины правильного многоугольника, называется его центральным углом. Все центральные углы правильного многоугольника равны между собой и составляют 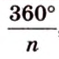

В правильном 

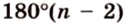
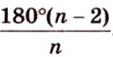
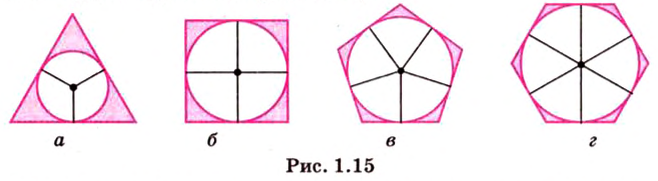
Окружность, вписанная в правильный многоугольник, касается его сторон в их серединах. Центр окружности, вписанной в правильный многоугольник, является точкой пересечения серединных перпендикуляров его сторон (рис. 1.15).
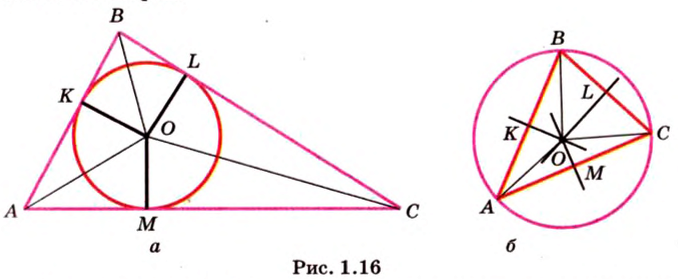
Простейшим многоугольником является треугольник. В любой треугольник можно вписать окружность, причем только одну. На рисунке 1.16, 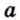
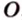

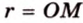
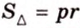
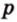
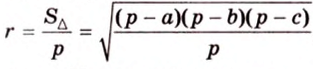
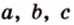
Можно ли в любой четырехугольник вписать окружность?
Ответ. Нельзя. В четырехугольник можно вписать окружность только при условии, что суммы длин его противоположных сторон равны.
Вокруг произвольного треугольника можно описать окружность, притом только одну (см. рис. 1.16, б). Центр окружности, описанной вокруг треугольника, является точкой пересечения серединных перпендикуляров, проведенных к его сторонам. Центр окружности 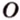
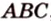
На рисунке 1.16, б изображена окружность с центром 
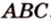
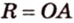
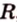
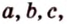
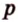
Можно ли описать окружность вокруг произвольного четырехугольника?
Ответ. Нельзя. Вокруг четырехугольника можно описать окружность только тогда, когда суммы противоположных углов равны 180°.
Треугольник и его элементы
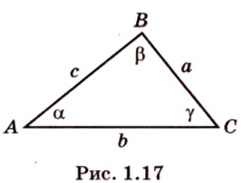
Треугольником называется фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, которые попарно соединяют эти точки. Рассмотрим 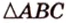
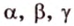
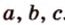
Треугольник называется тупоугольным, прямоугольным или остроугольным, если его наибольший внутренний угол соответственно больше, равен или меньше 90°.
Треугольник называется равнобедренным, если у него две стороны равны (боковые стороны). Основанием равнобедренного треугольника является сторона, которая не равна ни одной из двух других равных сторон.
Треугольник, все стороны которого равны, называется равносторонним, или правильным.
Соотношение между сторонами и углами треугольника:
Треугольник можно определить любой тройкой таких основных элементов: либо двумя сторонами и углом между ними, либо одной стороной и двумя углами, либо тремя сторонами.
Например, 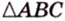
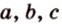
Соотношение между внутренними и внешними углами треугольника: любой внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Из трех отрезков можно образовать треугольник тогда и только тогда, когда любая его сторона меньше суммы и больше разности двух других его сторон. В любом треугольнике можно провести три медианы, три биссектрисы и три высоты.
Свойства биссектрисы угла треугольника: биссектрисы треугольника пересекаются в одной точке, которая лежит в середине треугольника и является центром вписанной
в него окружности.
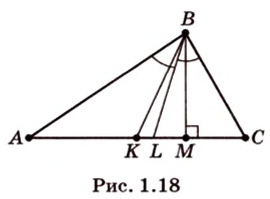
Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим к ней сторонам (рис. 1.18; 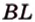
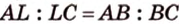
Основные свойства медиан треугольника:
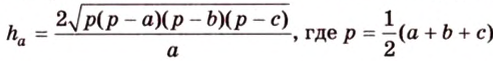
Медиана треугольника 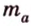
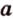
Свойства равнобедренного треугольника: углы при основании треугольника равны; высота, проведенная к основанию, является также биссектрисой и медианой.
Свойства равностороннего треугольника: все углы равны (каждый угол равен 60°); каждая из трех высот является также биссектрисой и медианой; центр окружности, описанной вокруг треугольника, совпадает с центром окружности, вписанной в него.
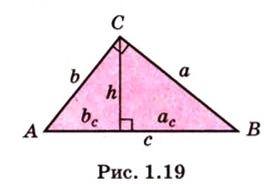
Стороны прямоугольного треугольника 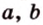
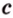
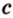
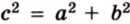
длины гипотенузы равен сумме квадратов длин катетов.
Свойства прямоугольного треугольника:
Выпуклые четырехугольники
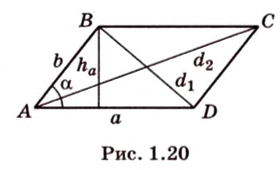
Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом (рис. 1.20).
Если в четырехугольнике исполняется любое из таких условий:
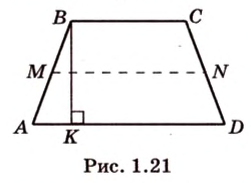
Если боковые стороны трапеции равны между собой, такую трапецию называют равнобокой (рис. 1.21; 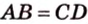
Равнобокая трапеция имеет такие свойства:
Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией (рис. 1.21; 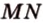
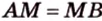
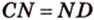
Средняя линия трапеции параллельна ее основаниям и равна их полусумме (рис. 1.21; 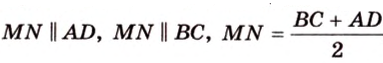
Задачи и методы их решения
Для геометрии закономерным является то, что введенные основные понятия и сформулированная аксиоматика составляют основу для новых утверждений. Однако справедливость последних необходимо доказывать путем определенных рассуждений, основывающихся на ранее доказанных утверждениях или аксиомах. Так формируются математические задачи.
Что такое математическая задача?
Можно ли утверждать, что для успешного решения геометрических задач и доказательства теорем достаточно свободно владеть всем теоретическим материалом?
Нет. Это не так. При хорошем знании теории следует овладеть еще и практическими навыками. А это возможно только в процессе решения задач, начиная с простейших и постепенно переходя к более сложным.
Математические задачи условно разделены на четыре вида, в соответствии с их требованиями: задачи на вычисление, доказательство, исследование и построение. С ними вы уже ознакомились в курсе планиметрии.
Приступая к решению задачи, следует выбрать метод. Методы делят:
Суть синтетического метода заключается в том, что, исходя из условия задачи или теоремы с использованием известных утверждений строится цепочка логических рассуждений, последнее из которых совпадает с требованием задачи. Приведем пример.
Пример №1
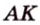
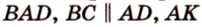
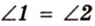
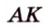
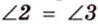
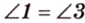
В 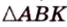
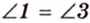
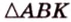
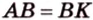
1. Если 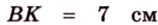
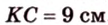
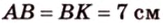
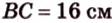
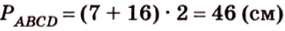
2. Если 
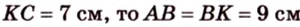
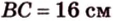
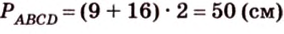
Ответ. 46 см или 50 см.
Эта задача является опорной, поскольку на такой идее строятся многие задачи и для параллелограмма, и для трапеции. У этих фигур биссектриса угла отсекает всегда равнобедренный треугольник.
Отметим, что сокращенное обозначение углов в виде 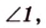
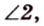
Как видим, в процессе решения задачи 1 используются только известные геометрические утверждения и производятся соответствующие вычисления. Причем для каждой геометрической задачи такие рассуждения свои.
Суть аналитического метода состоит в том, что, исходя из требования (вывода) утверждения (теоремы или задачи) и опираясь на известное утверждение, строится цепочка логических рассуждений, которая показывает, что требование является следствием условия. Приведем пример.
Пример №2
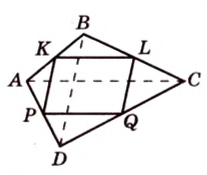
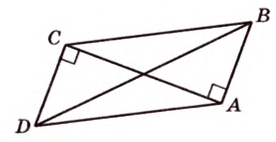
Докажите, что середины сторон любого выпуклого четырехугольника являются вершинами параллелограмма.
Дано: 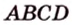

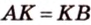
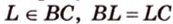

Доказать: 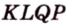
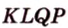
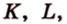
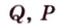
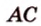
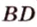
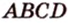
В 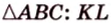
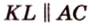
В 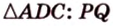

Имеем: 1. 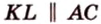
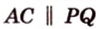
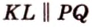
Чтобы решить задачу прямым методом, следует начать с анализа содержания задачи, от которого зависит выбор метода решения. Далее необходимо создать модель в виде рисунка и продолжить рассуждать над каждым действием, которые в совокупности образуют цепочку действий, ведущих либо от условия к требованию, либо от требования к условию.
Суть метода доказательства от противного состоит в том, что, имея утверждение, строим новое, возразив выводу данного. Формулируется утверждение. Исходя из вывода противоположного утверждения, строим цепочку истинных утверждений, пока не получим утверждение, которое противоречит либо условию, либо известной аксиоме или теореме, либо предположению. Таким образом приходим к выводу, что противоположное утверждение ошибочно, а потому исходное является истинным (тут действует логический закон: из двух противоположных утверждений одно истинное, другое ошибочное, третьего не дано). Рассмотрим пример.
Пример №3
Докажите утверждение: если две прямые параллельны третьей, то они параллельны между собой.
Строим противоположное утверждение: существуют две прямые, параллельные третьей и не параллельные между собой.
Математическую задачу считают решенной, если:
Метод от противного называют непрямым методом решения математических задач.
Рассмотрим некоторые другие методы решения геометрических задач, которые делят на виды по использованию математического аппарата.
Алгебраический метод решения задач
Решая задачу алгебраическим методом, следует уделить внимание таким этапам:
Приведем другие примеры решения задач алгебраическим методом.
Пример №4
Периметр прямоугольного треугольника равен 36 см. Гипотенуза относится к катету как 5 : 3. Найдите стороны треугольника.
Дано: 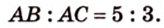
Найти:
Обозначим коэффициент пропорциональности через 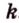
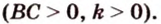
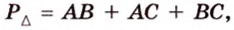
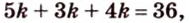
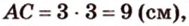
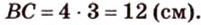
Ответ. 15 см, 9 см и 12 см.
Почему именно так?
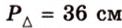
Пример №5
В параллелограмме диагонали равны 16 см и 20 см. Меньшая из них перпендикулярна к его стороне. Найдите площадь этого параллелограмма.
Дано: 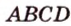
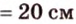
Найти:
Почему именно так?
Пусть 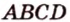
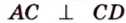
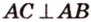
Обозначим стороны параллелограмма: 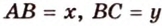
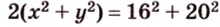
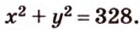
По теореме Пифагора из 
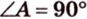
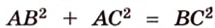
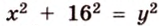
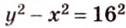
Составим систему уравнений:
Ответ.
В ходе решения этой задачи сначала выбираем формулу для вычисления площади параллелограмма. 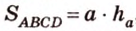
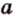
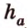
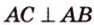
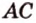
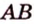
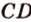
Метод площадей
Пример №6
Стороны треугольника равны 13 см, 14 см и 15 см. Вычислите высоту, проведенную к стороне, которая имеет длину 14 см.
Пусть 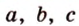
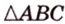
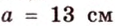
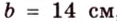
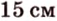
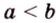
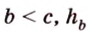
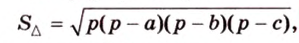
Ответ. 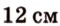
Имея три стороны треугольника 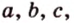
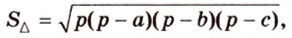
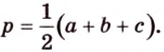
С другой стороны, площадь треугольника можно найти по формулам: 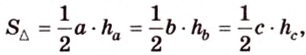
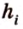

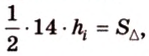
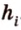
Отметим, что хотя во время решения задачи 6 использовалось алгебраическое уравнение, более существенными в решении этой задачи являются рассуждения о площади фигуры. Поэтому такой метод получил название метод площадей.
Пример №7
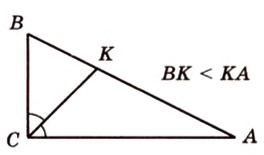
Катеты прямоугольного треугольника равны 3 см и 6 см. Найдите длину биссектрисы прямого угла.
Дано: 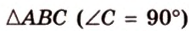
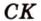
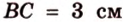
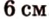
Найти: 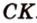
Пусть 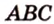
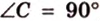
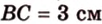
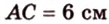
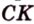
Введем обозначение: 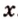
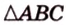
Площадь 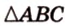
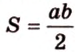
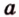
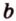
Биссектриса разделила 
где 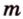
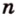
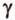
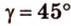
Поскольку 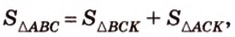
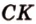
Метод векторов
Чтобы применить метод векторов к решению задачи, необходимо выполнить следующие действия:
Пример №8
Докажите, что середины сторон любого выпуклого четырехугольника являются вершинами параллелограмма.
Дано: 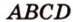
Доказать: 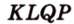
1. Переведем задачу на язык векторов, заменив отрезки векторами: 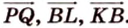
2. Воспользуемся правилом треугольника для сложения векторов: 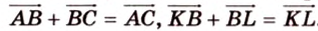
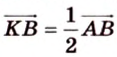
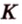
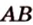
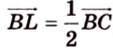
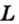
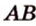
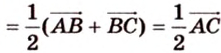
Поэтому 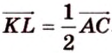
Аналогично 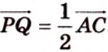
3. Поэтому 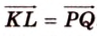
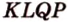
Переведя задачу на язык векторов, получаем требование задачи: доказать равность векторов 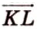
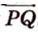
Однако 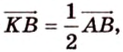
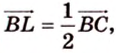
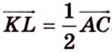
Аналогично получаем, что 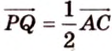
Таким образом, 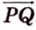
Метод координат
Решая задачу координатным методом, следует выполнить такие действия:
Методом координат чаще всего решают задачи:
Решая задачу методом координат, необходимо рационально выбрать систему координат: данную фигуру следует разместить относительно осей координат таким образом, чтобы как можно больше координат нужных точек равнялось нулю, а также одному и тому же числу. Например, координаты вершин прямоугольника 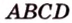
Проиллюстрируем суть метода координат на примере.
Пример №9
Докажите, что когда у параллелограмма диагонали равны, то он прямоугольник.
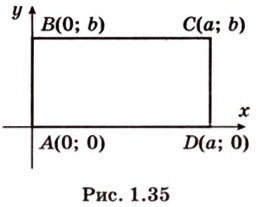
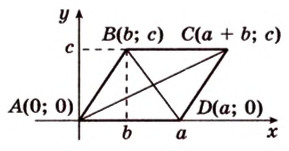
Разместим параллелограмм в системе координат таким образом, чтобы его вершины имели координаты: 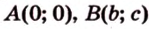
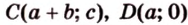
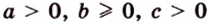
По условию 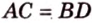
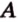
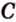
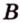
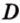
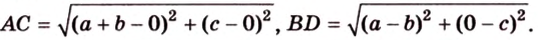
Тогда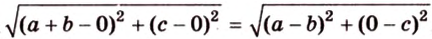
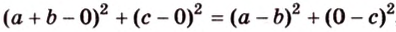
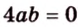
Поскольку 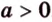
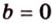
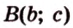
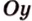
Поэтому угол 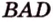
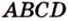
Метод геометрических преобразований: метод поворота, метод симметрии, метод параллельного переноса, метод гомотетии.
Решая задачи методом геометрических преобразований, наряду с данными фигурами рассматривают новые, полученные из данных с помощью определенного преобразования. Выясняют свойства новых фигур, переносят эти свойства на данные фигуры, а затем находят способ решения задачи.
Говорят, что задачи, решенные методами векторов, координат, геометрических преобразований, площадей и другими методами, в которых используется больше свойств геометрических фигур, решены геометрическими методами.
Второй период — формирование геометрии в структурную систему. В VII в. до н.э. центром развития геометрии стала Греция. Древние геометры работали над систематизацией накопленных и новых знаний, устанавливали связи между геометрическими фактами, разрабатывали приемы доказательств. Значительный вклад в развитие математики, в частности геометрии, в этот период сделали Пифагор, Платон, Аристотель, Фалес, Анаксигор, Демокрит, Евклид. В книге «Начала» Евклида сформулированы понятия о фигуре, о геометрическом утверждении и доказательстве. Они остаются актуальными и сегодня.
Особенность начатого Н.И. Лобачевским периода в истории геометрии состоит в том, что после его открытия начали развиваться новые геометрические теории, новые «геометрии» и соответствующие обобщения самого предмета геометрии. В этот период возникло понятие о разновидностях пространства (термин «пространство» в науке может означать как обычное реальное пространство, так и абстрактное, «математическое», пространство). Некоторые теории создавались внутри евклидовой геометрии, как ее особые разделы, а позднее приобретали статус самостоятельных. Другие, подобно геометрии Лобачевского, вводили изменения аксиом и структурировались на основе этих изменений, обобщая и строя науку.
В школьном курсе мы изучаем геометрию Евклида. Перевел труд древнегреческого ученого «Начала» украинский математик Михаил Егорович Ващенко-Захарченко (1825-1912) в 1880 г. На основе этой книги написано множество учебников по геометрии. Например, преподавание геометрии в советской школе почти до 1982 г. осуществлялось по учебнику российского педагога-математика А.П. Киселева (1852-1940). В 1980-х годах украинским математиком А.В. Погореловым было создано новое учебное пособие. Его и сегодня можно найти в библиотеках общеобразовательных учебных заведений.
Современная геометрия является многовекторной и стремительно развивается в совокупностях математических теорий, изучающих различные пространства и их фигуры. Значительный вклад в геометрию сделали и наши соотечественники: М.В. Остроградский, А.М. Астряб, А.П. Киселев, А.Д. Александров, А.Н. Колмогоров, А.В. Погорелов и др.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.