Что такое пластический шарнир

ПЛАСТИЧЕСКИЙ ШАРНИР

Полезное

Смотреть что такое «ПЛАСТИЧЕСКИЙ ШАРНИР» в других словарях:

пластический линейный шарнир пластинки — Сечение, во всех точках которого нормальные напряжения по всей толщине пластинки достигают предела текучести. [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] … Справочник технического переводчика

шарнир пластический — Предельное состояние сечения конструкций, при котором напряжения по всему сечению равны пределу текучести [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] Тематики строительная механика, сопротивление материалов EN … Справочник технического переводчика

ШАРНИР ПЛАСТИЧЕСКИЙ — предельное состояние сечения конструкций, при котором напряжения по всему сечению равны пределу текучести (Болгарский язык; Български) пластична става (Чешский язык; Čeština) plastický kloub (Немецкий язык; Deutsch) plastisches Gelenk (Венгерский … Строительный словарь

ПРОТЕЗЫ — (от греч. protithemi замещаю), механические приборы, приспособления и аппараты, возмещающие различные дефекты и скрадывающие повреждения отдельных частей тела. В большинстве случаев протезы являются функционально косметическими приборами,… … Большая медицинская энциклопедия

Источник

Пластический шарнир

Статически неопределимые балки и плиты железобетонных перекрытий рассчитывают с учетом перераспределения внутренних усилий, которое может происходить вследствие образования трещин, проявления неупругих свойств бетона и арматуры, а также частичного нарушения сцепления арматуры с бетоном. Это позволяет принять наиболее рациональную схему армирования элементов, а в ряде случаев снизить расход арматуры. Рассмотрим сущность такого расчета.

По мере увеличения внешней нагрузки напряжения в сечениях железобетонного элемента увеличиваются. Когда в наиболее напряженном сечении растянутая арматура достигает напряжений, равных пределу текучести, бетон сжатой зоны, имея высокие напряжения, испытывает значительные неупругие деформации. Такое напряженное состояние, возникшее в одном из сечений статически определимого элемента, приводит к повороту двух его частей (расположенных справа и слева от сечения), в результате которого напряжения в бетоне достигают временного сопротивления сжатию и наступает разрушение.

Если напряжения растянутой арматуры достигают предельных в каком-либо сечении статически неопределимого элемента, то разрушения в этом сечении не происходит, так как повороту примыкающих участков элемента препятствуют опорные закрепления, В рассматриваемом сечении происходят значительные местные деформации, но оно воспринимает момент

где A_s – площадь сечения арматуры; z – плечо внутренней пары сил.

Для расчета этот момент принимают равным:

Участок балки, испытывающий указанное напряженное состояние, называют пластическим шарниром. При дальнейшем увеличении нагрузки на элемент момент в пластическом шарнире остается постоянным, а в других сечениях возрастает, т. е. происходит перераспределение моментов.

Пластические шарниры могут образовываться в нескольких сечениях элемента, до тех пор пока он не станет статически определимым, тогда образование еще одного пластического шарнира приведет к разрушению.

Для иллюстрации сказанного рассмотрим однопролетную статически неопределимую балку с защемленными концами пролетом l, загруженную равномерно распределенной нагрузкой q.

Предельные моменты, воспринимаемые пролетными и опорными сечениями балки, равны;

Сумма пролетного и опорного моментов в статически неопределимых балочных системах равна моменту свободно лежащей балки М_о:

При равномерно распределенной нагрузке

В рассматриваемом случае

По упругому расчету такой балки опорные моменты M_оп=q·l 2 /12, а момент в середине пролета M_пр=q·l 2 / 24 (М_пл + М_оп =q·l 2 /8=М_о). Если количество арматуры, поставленное в опорных сечениях балки, будет меньшим, чем это требуется по указанной выше величине опорного момента, то в процессе загружения при нагрузке q₁ 2 /16, в пролете надо поставить арматуру на момент

Дата добавления: 2015-02-03 ; просмотров: 4341 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Пластические шарниры в железобетонных конструкциях

Рассмотрим, что произойдет, если мы постепенно будем увеличивать внешнюю нагрузку, увеличивая тем самым изгибающий момент. При этом напряжения в арматуре будут возрастать, пока не достигнут предела текучести. После достижения предела текучести напряжения в арматуре не будут возрастать, при этом происходит удлинение арматуры без увеличения напряжений (текучесть арматуры или пластические деформации).

Из-за удлинения арматуры будет происходить поворот элементов железобетонной конструкции разделенных трещиной. Данное явление называют пластическим шарниром.

Пластический шарнир – такое напряженно-деформированное состояние сечения элемента, при котором напряжения в растянутой арматуре равны пределу текучести, а напряжения в бетоне сжатой зоны менее предельных.

Сходство пластического шарнира с «обычным» шарниром, принимаемым в теоретической механике и смежных науках, состоит в том, что в сечении с трещиной в данном случае происходит поворот частей конструкции друг относительно друга.

Отличие пластического шарнира от «обычного» состоит в том, что в пластическом шарнире изгибающий момент не равен нулю, так как напряжения в арматуре и бетоне отличны от нуля. Также отличием будет и то, что после снятия нагрузки пластический шарнир не вернется в исходное состояние, так как арматура растянутой зоны претерпевает пластические деформации и сокращается лишь на величину упругих деформаций.

Определить изгибающий момент в пластическом шарнире несложно.

Таким образом, изгибающий момент в сечении железобетонного элемента не может превысить момент образования пластического шарнира ни при каких условиях (если не рассматривать зону упрочнения после площадки текучести).

Подобно тому, как для арматурной стали составляют диаграмму «напряжения-деформации», для сечения железобетонного элемента можно составить диаграмму и «изгибающий момент-кривизна».

Отметим, что поскольку изгибающий момент можно с некоторым приближением считать пропорциональным напряжениям в растянутой арматуре, а кривизну железобетонного элемента с трещиной пропорциональной удлинению данной арматуры, то в целом вид диаграммы «изгибающий момент-кривизна» будет похож на вид диаграммы «напряжения-деформации» для арматурной стали.

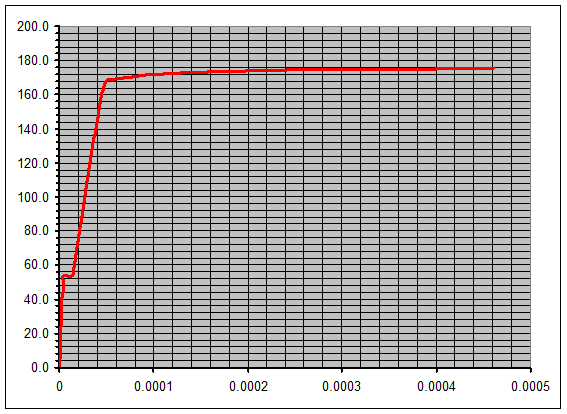
Диаграмма «изгибающий момент-кривизна» для железобетонного элемента.

На диаграмме «изгибающий момент-кривизна» можно выделить 3 характерных участка:

1. Участок работы без трещин. На данном этапе кривизна и изгибающий момент монотонно возрастают, при этом жесткость соответствует жесткости приведенного сечения.

2. Участок работы железобетонного элемента с трещинами в растянутой зоне до достижения напряжениями в арматуре предела текучести.

3. Участок работы железобетонного элемента после достижения напряжениями в арматуре предела текучести.

Отметим, что после образования начала текучести растянутой арматуры на диаграмме заметно некоторое увеличение изгибающего момента. Данное увеличение вызвано тем, что при увеличении раскрытия трещина сжатая зона уменьшается по высоте, что приводит к увеличению расстояния между равнодействующими в растянутой арматуре и сжатой зоне бетона (плеча внутренней пары сил) и, соответственно, увеличению изгибающего момента без увеличения собственно усилия в арматуре. Однако данное увеличение изгибающего момента достаточно мало, в связи с чем им, как правило, пренебрегает.

Подобно тому, как для арматурной стали часто реальную диаграмму «напряжения-деформации» представляют в виде двухлинейной зависимости с идеальной площадкой текучести (диаграмма Прандтля), для железобетонного элемента в большинстве случаев с достаточной для практических целей точности можно принимать двухлинейную диаграмму «изгибающий момент-кривизна».

В этом случае пренебрегают следующими факторами:

1. Участок работы без трещин. В самом деле – в большинстве случаев момент образования трещин значительно меньше момента образования пластического шарнира, поэтому данным участком диаграммы можно пренебречь.

2. Увеличение изгибающего момента после начала текучести рабочей арматуры. Причем изгибающий момент при этом оценивают «сверху», т.е. принимая за момент в пластическом шарнире изгибающий момент разрушения сечения, а не начала текучести арматуры.

Введение данных упрощений позволяет значительно облегчить учет пластических шарниров при расчете статически неопределимых железобетонных конструкций. Отметим, что современные программные комплексы позволяют учитывать диаграммы «изгибающий момент-кривизна» весьма сложного вида, однако в инженерной практике применением таких методов вряд ли оправдано. Кроме того, данные решения трудно поддаются контролю правильности решения и имеют математические трудности решения – «ложное» отсутствие сходимости итераций в случае, когда принципиально решение задачи существует, но программный комплекс в силу определенных настроек алгоритма не может его найти. Поэтому для решения таких задач следует не только хорошо представлять работу железобетонной конструкции, но и быть специалистам по численным методам и, зачастую, специалистом по программированию.

Двухлинейная диаграмма «изгибающий момент-кривизна» для железобетонного элемента.

С учетом введенных ранее предпосылок отметим конструкции, в которых возможно допустить образование пластических шарниров:

1. Конструкции, в которых арматура растянутой зоны имеет ярковыраженную площадку текучести.

2. Конструкции, в которых напряжения в растянутой арматуре раньше достигают предела текучести, чем напряжения в бетоне сжатой зоне достигают предельного значения (точнее говорить «деформации бетона сжатой зоны достигают предельных значений»). Для того, чтобы удлинение растянутой арматуры не вызывало чрезмерное сжатие бетона крайнего сжатого «волокна» вследствие взаимного поворота частей конструкции, граничное значение высоты сжатой зоны рекомендуется снижать умножением на коэффициент 0,7.

Источник

Что такое пластический шарнир

115. Что такое пластический шарнир?

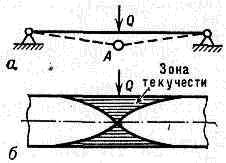
Когда напряжения в растянутой арматуре достигают предела текучести, усилие в ней перестает расти (Ns = Npl = const), по условию статики не растет и усилие в сжатом бетоне (Nb = Ns). Поскольку плечо z внутренней пары сил практически также не меняется, то не растет и момент, воспринимаемый нормальным сечением: Mpl = Nbz = const. Однако деформации арматуры es продолжают увеличиваться (арматура течет), в связи с чем примыкающие к сечению части изгибаемого элемента взаимно поворачиваются (см. узел А на рис. 60) – сечение работает как шарнир, но, в отличие от обычного (в котором момент равен нулю), способный воспринимать изгибающий момент Mpl. Такое состояние сечения назвали «пластическим шарниром» (ПШ).

Понятно, что ПШ может возникнуть только в слабо армированном сечении. В переармированном сечении арматура предела текучести не достигает (см. вопрос 62), а в нормально армированном достижение предела текучести происходит одновременно с разрушением бетона сжатой зоны и о взаимном повороте примыкающих частей речи быть не может.

В статически определимой конструкции (например, в однопролетной балке) образование ПШ превращает ее в механизм и быстро вызывает разрушение (рис. 60,а). Иное дело в статически неопределимых системах: образование ПШ там только устраняет лишнюю связь, и чем больше лишних связей, тем большее число ПШ можно допустить без риска разрушения конструкции (рис. 60,б). Поскольку в ПШ моменты не растут, то при увеличении нагрузки начинают более интенсивно работать другие сечения, происходит т.н. «перераспределение моментов» с одних сечений на другие. Перераспределение продолжается до наступления предельного равновесия, за которым система превращается в механизм.

116. Как происходит перераспределение моментов?

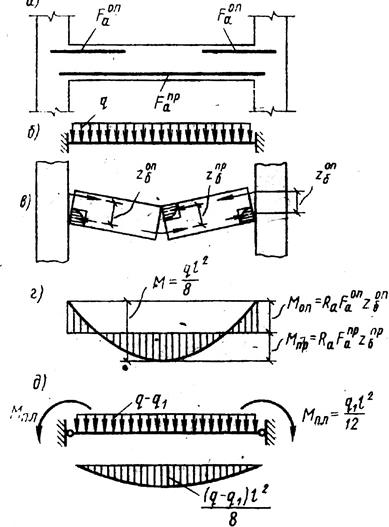
Рассмотрим защемленную балку с одинаковой продольной растянутой арматурой в пролете и на опорах (As = A´s), нагруженную нагрузкой q (рис. 61). На 1-ом этапе нагружения моменты в балке распределяются согласно правилам строительной механики и растут пропорционально нагрузке. Так продолжается до тех пор, пока в опасных сечениях (в данном примере – на опорах) не потечет растянутая арматура S´ и не возникнут ПШ. Тогда моменты в последних достигают величины M´1 = –ql2 /12, а в пролете – величины M1 = ql2/24 – это окончание работы конструкции по упругой статической схеме.

При дальнейшем увеличении нагрузки (2-й этап) в опорных сечениях арматура S´ продолжает течь, опорные моменты не растут (M´1 =–ql2/12 = const), зато растут моменты в пролете, пока не достигают предельного значения:M2=ql2/12 (напомним, что несущая способность пролетного и опорных сечений в данном примере одинакова). Наступает предельное равновесие: в пролете образуется еще один ПШ, вслед за чем балка превращается в механизм (три шарнира на одной прямой) и происходит разрушение.

В результате упруго-пластической работы и перераспределения усилий, пролетный момент увеличился вдвое по сравнению с упругой схемой, а нагрузка q возросла в 1,33 раза. Удостовериться в этом легко, если вспомнить правило строительной механики: суммарное значение пролетного и полусуммы опорных моментов равно моменту в однопролетной свободно опертой балке Мб. Тогда на 1-ом этапе Мб1 = ql2 /12 +ql2/24 = = 3ql2/24 = ql2/8, на 2-м этапе Мб2 = ql2 /12 + ql2 /12 = 4ql2/24 = 1,33 ql2/8.

117. Можно ли заранее планировать перераспределение моментов?

В предыдущем примере показано, как с помощью ПШ удалось выровнять опорные и пролетный моменты и увеличить нагрузку на балку. Такие задачи встречаются не часто, обычно нагрузка известна заранее. Тогда ПШ можно использовать по-другому, а именно: выровнять опорные (M´1 = ql2 /12) и пролетный (M1 = ql2/24) моменты, передвинув параллельно вниз всю эпюру (рис. 62). Поскольку |M´1| + M1=ql2/12 +ql2/24 = =ql2/8, то после выравнивания M2 = –M´2 = ql2 /16. По сравнению с упругой схемой опорные моменты M´2 снизились на 1/4, а пролетныйM2 вырос на 1/2. Очевидно, что эпюра моментов оказалась передвинутой вниз на величину DM = ql2 /48, что равносильно добавлению к существующей упругой эпюре еще одной эпюры DM со знаком«+» (рис. 62).

Именно так и поступают в практике проектирования, а эпюру DM называют «добавочной». Ординаты эпюры DM имеют одно ограничение: они не должны превышать 30 % значений того максимального упругого момента, который предстоит снижать. Таким образом, с помощью добавочных эпюр можно заранее запланировать перераспределение моментов. Форма добавочной эпюры зависит от расчетной схемы конструкции. Например, у двухпролетной свободно опертой неразрезной балки она будет треугольной, так как на крайних опорах моменты возникать не могут.

118. Какой смысл в перераспределении моментов?

Если основываться на предыдущем примере, то, действительно, смысла нет. Ведь уменьшение опорных моментов влечет увеличение пролетного, т.е. экономия опорной арматуры приводит к перерасходу пролетной. Есть, правда, исключение: в многопролетных неразрезных плитах монолитных перекрытий выравнивание моментов дает возможность применять рулонные сетки (т.е. арматуру одного сечения) по всей длине, что значительно упрощает технологию армирования.

Эффект от ПШ и перераспределения моментов проявляется тогда, когда к конструкции приложены временные нагрузки, действующие по разным схемам. Рассмотрим в качестве примера двухпролетную неразрезную балку с равными пролетами по 6 м (рис. 63), испытывающую воздействие постоянной (g = 8 кН/м) и временной (v = 24 кН/м) нагрузок. Нагрузка может быть приложена по одной из трех схем.

Схема 1 – постоянная плюс временная по всей длине: опорный момент составляет –144 кН×м, пролетные моменты +81 кН×м. Схема 2 – постоянная плюс временная на левом пролете: опорный момент – 90 кН×м, пролетный в левом пролете +103 кН×м, в правом пролете +1,1 кН×м. Схема 3 – постоянная плюс временная на правом пролете: эта эпюра зеркальна эпюре 2, потому на рисунке не приведена. Схема 1 создает максимальный (по модулю) опорный момент, схемы 2 и 3 – максимальные пролетные моменты.

Предусмотрим образование ПШ на средней опоре при нагружении по схеме 1 и с помощью добавочной эпюры DM уменьшим опорный момент на 30 %: 144 – 43 =101 кН×м. При этом максимальные пролетные моменты выросли с 81 до 98 кН×м, а опасные пролетные сечения передвинулись с расстояния 2,25 м на 2,48 м от крайних опор. При нагружении по схеме 2 (и 3) вводить ПШ на опоре нет смысла, т.к. упругий опорный момент 90 кН×м и так меньше опорного момента 101 кН×м, полученного после перераспределения по схеме 1. Казалось бы, есть смысл уменьшить пролетные моменты со 103 до 98 кН×м, т.е. «подтянуть» их до уровня перераспределенных моментов по схеме 1 (несколько увеличив опорный момент 90 кН×м). Однако делать этого нельзя вот по какой причине: уменьшение пролетных моментов предусматривает образование в пролетах ПШ, а это означает, что при нагружении по схеме 1 в балке одновременно возникнут три ПШ, она превратится в механизм и разрушится. Чтобы этого не произошло, пролетные моменты по схемам 2 и 3 уменьшать нужно так, чтобы они были больше моментов по схеме 1. В нашем примере можно уменьшить пролетные моменты, например, до 101 кН×м, приравняв их к опорному по схеме 1. Для этого строим добавочную отрицательную эпюру DM, в результате чего опорный момент возрастает до 94,7 кН×м, что меньше перераспределенного момента по схеме 1. В итоге, при нагружении по 1-й схеме ПШ образуется на опоре, по 2-й схеме – в левом пролете, по 3-й схеме – в правом пролете.

Для кого выпускается наша продукция и меры ее эксплуатации.

Источник

Что такое пластический шарнир

В промежуточных стадиях между появлением фибровой текучести (рис. 24, а) и образованием шарнира пластичности (рис. 24, в) пластические деформации занимают только крайние части сечения, оставляя около нейтральной оси упругое ядро (рис. 24, б).

В этом случае изгибающий момент может быть получен как разность предельного момента и момента напряжений, косо заштрихованных на эпюре (рис. 24, г)
(14)

где sт Wa—момент напряжений соответствующей эпюры;

-отношение протяженности упругой зоны к высоте сечения; k—коэффициент, зависящий от формы сечения;

Нетрудно видеть, что для прямоугольного сечения

где b — ширина сечения.

Отсюда k=1/3. Для двутаврового сечения k близко к 0,1. Обычно принимается, что закон плоских сечений сохраняет силу и при пластических деформациях, т. е.

где eт —удлинение при фибровой текучести;e—удлинение на крайней фибре сечения (рис. 24, б).

Следовательно, момент М можно представить как
(15)

Таким образом, момент в пределах упругопластической области работы сечения является гиперболической функцией удлинения крайней фибры e, имея своей асимптотой момент Мпр (рис. 25).

Отсюда следует, что величине Мпр отвечает бесконечно большое удлинение крайней фибры, так что фактически предельный момент и шарнир пластичности полностью проявиться не могут.

Однако можно показать, что на протяжении площадки текучести шарнир пластичности может проявиться в достаточной мере. Действительно, площадка текучести малоуглеродистых сталей имеет протяжение по удлинениям от 0,15 до 3%. Возьмем среднюю точку на площадке текучести и положим e = 1,5%; для начальной точки площадки eт = 0,15%. Тогда изгибающий момент для прямоугольного сечения [см. формулу (15)] будет,

что только на 1/3% меньше предельного момента; для двутаврового сечения он будет меньше предельного на 1/10%.Если материал не имеет площадки текучести, шарнир пластичности образоваться не может и напряжения возрастают до разрушения. Эпюра напряжений при изгибе в упругопластической области имеет вид, указанный на рис. 26, а; в предельном случае при бесконечно больших удлинениях,—на рис. 26, б.

Рис. 25. Зависимость изгибающих моментов от удлинений крайней фибры в упругопластической области

Добавочный треугольник зависит от модуля пластических деформаций и весьма невелик. При что отвечает работе материала из алюминиевых сплавов, увеличение предельного момента получается

6%.

Рис. 26. Распределение напряжений при пластической работе балки и отсутствии площадки текучести

Рис. 27. Зона пластичности около шарнира пластичности при изгибе балки

Когда в балке действуют изгибающие моменты и поперечная сила (т. е. балка работает не на чистый изгиб), шарнир пластичности образуется в точке максимума моментов (в балке постоянного сечения) и там возникает предельный момент . В соседних сечениях, между точками эпюры моментов, в которых величина момента

Мф = sт W отвечает фибровой текучести (рис. 27), пластические деформации занимают часть сечения балки в соответствии с эпюрой напряжений, постепенно проникая внутрь сечения балки и образуя около шарнира пластичности область пластического состояния материала балки.

Источник