Что такое площадь ромба
Как найти площадь ромба
Площадь ромба можно вычислить разными способами.
Например, через половину произведения двух диагоналей
друг на друга, через синус и сторону в квадрате…
Также, площадь ромба равна площади параллелограмма.
Как следствие, так, как ромб является параллелограммом, с
равными сторонами, поэтому площадь ромба
можно найти через площадь параллелограмма.
Для ромба истинны и верны все свойства параллелограмма.
Формула площади ромба и формула
площади параллелограмма одинаковая.
Ромб — параллелограмм, у которого
все четыре стороны равны.
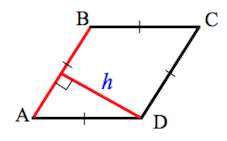
Формулировка площади ромба через параллелограмм:
Формула площади ромба через параллелограмм:
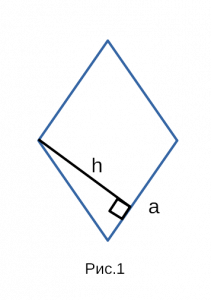
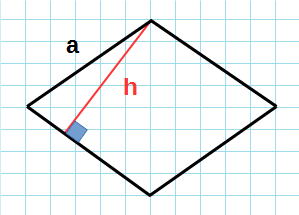
a — основание; h — высота;
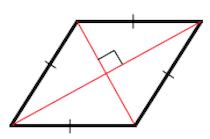
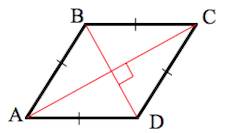
Площадь ромба, можно также найти другим способом. Для
этого мысленно разделим ромба на четыре треугольника,
так чтобы каждая вершина была соединена с противоположной
вершиной. Получившиеся линии называют диагоналями. Если
известны длины двух диагоналей ромба, то можно найти площадь.
Формула площади ромба через две диагонали:
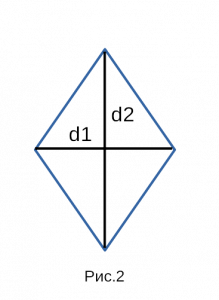
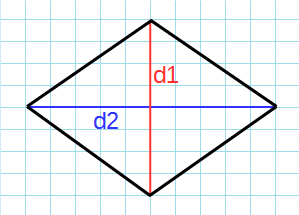
d1 и d2 — диагонали;
В самых редких случаях, если известен синус и одна из сторон,
используют формулу площади ромба через синус и квадрат стороны.
Формулировка площади ромба через синус и сторону в квадрате:
Формула площади ромба через синус и сторону в квадрате:
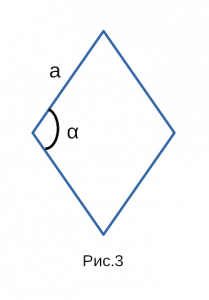
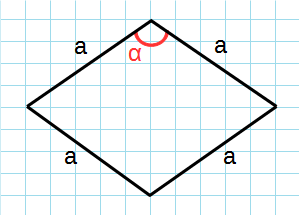
a — сторона; sin α — синус угла;
Рис. 1 — площадь ромба через площадь параллелограмма / основание и высоту.
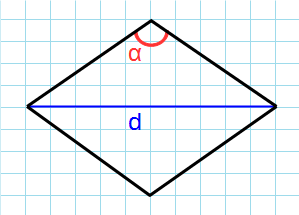
Рис. 2 — площадь ромба через две диагонали
Рис. 3 — площадь ромба через синус и сторону в квадрате
Также, вы можете прочитать про свойства и признаки ромба.
Ромб. Свойства и признаки ромба
Ромб – это параллелограмм, у которого все стороны равны.
Если у ромба – прямые углы, то он называется квадратом.
Свойства ромба
1. Поскольку ромб – это параллелограмм, то все свойства параллелограмма верны для ромба.
Помимо этого:
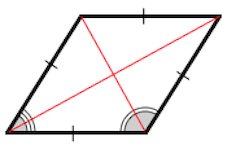
2. Диагонали ромба перпендикулярны.
3. Диагонали ромба являются биссектрисами его углов.
4. Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.
Признаки ромба
Чтобы параллелограмм оказался ромбом, необходимо выполнение одного из следующих условий:
1. Все стороны параллелограмма равны между собой ().
2. Диагонали пересекаются под прямым углом ().
3. Диагонали параллелограмма являются биссектрисами его углов.
Площадь ромба
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Как рассчитать площадь ромба
На данной странице калькулятор поможет рассчитать площадь ромба онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.
Ромб – четырёхугольник, у которого все стороны равны между собой. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом.
Через сторону и высоту
Формула для нахождения площади ромба через сторону и высоту:
Через диагонали
Формула для нахождения площади ромба через диагонали:
Через сторону и угол
Формула для нахождения площади ромба через сторону и угол:
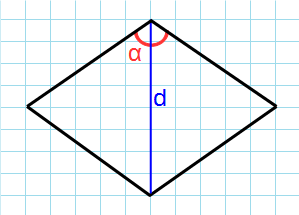
Через угол и диагональ из этого угла
Формула для нахождения площади ромба через угол и диагональ выходящая из этого угла:
Через угол и противолежащию диагональ
Формула для нахождения площади ромба через угол и диагональ противолежащая углу:
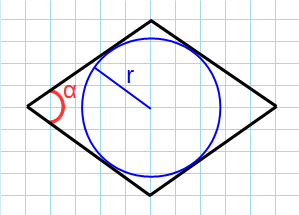
Через угол и радиус вписанной окружности
Формула для нахождения площади ромба через угол и радиус вписанной окружности:
Ромб. Формулы, признаки и свойства ромба
 |  |
| Рис.1 | Рис.2 |
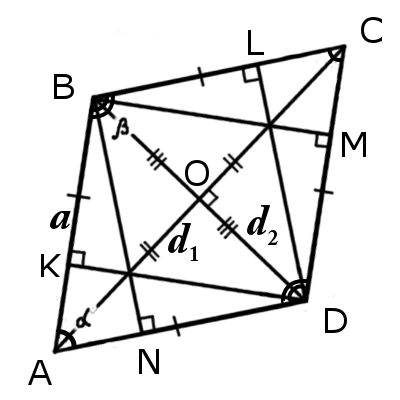
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
Сторона ромба
Формулы определения длины стороны ромба:
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 2 = a √ 2 + 2 · cosβ
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
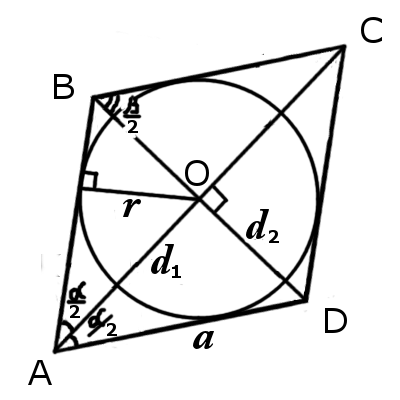
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Площадь ромба – формула, пример расчет, как начертить
Через диагонали
 |  |
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Свойства ромба
В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей. Радиус окружности равен половине высоты ромба:
Формула вычисления площади
1. По длине стороны и высоте:
Площадь ромба (S) равняется произведению длины его стороны и высоты, проведенной к ней:
S = a*h
2. По длине стороны и углу
Площадь ромба равняется произведению квадрата длины его стороны и синуса угла между сторонами:
S = a 2 *sin α
3. По длинам диагоналей
Площадь ромба равна одной второй произведения его диагоналей.
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
Примеры задач
Задание 1
Найдите площадь ромба, если длина его стороны равна 10 см, а высота, проведенная к ней – 8 см.
Задание 2
Найдите площадь ромба, сторона которого равняется 6 см, а острый угол – 30°.
Задание 3
Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно.
Через основание и высоту
 |  |
Площади фигур
Площадь ромба по углу и противолежащей диагонали
Площадь ромба по углу и диагонали проведенной из этого угла
Способ расчета площади ромба
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: 
где a – стороны, h – высота
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: 
где d1, d2 – диагонали
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: 
где a – сторона, α – угол между сторонами
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: 
где r – радиус вписанной окружности, α – угол между сторонами
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: 
где r – радиус вписанной окружности, a – сторона
Формула площади ромба через две стороны и угол между ними
Найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам.
Решение
По формуле получаем:
S = a 2 ⋅ sin ( α ) = 1 0 0 ⋅ sin ( 3 0 ∘ ) = 5 0 (см. кв.)
Ответ: 50 см. кв.
Формула площади ромба через угол и радиус вписанной окружности
Формула площади ромба через сторону и угол
Таблица с формулами площади ромба
В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула |
| 1 | сторона и высота |  |
| 2 | диагонали |  |
| 3 | диагональ и угол между сторонами |  |
| 4 | диагональ и угол между сторонами |  |
| 5 | сторона и угол между сторонами |  |
| 6 | радиус вписанной окружности и угол между сторонами |  |
| 7 | сторона и радиус вписанной окружности |  |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.