Что такое площадь сферы
Формулы площади поверхности геометрических фигур
Применение формулы
Рассмотрим на примере, как вычислить площадь круглого шара, диаметр которого равен 50 см. Следуя формуле, нужно 50 разделить на два (чтобы получить радиус), возвести полученное число в квадрат и умножить всё это дело сначала на 4, затем на 3,14. В итоге получим число в 7 850 квадратных сантиметров.
Формула вычисления площади применяется не только среди учителей в школе и научных сотрудников в лаборатории. Данная формула может пригодиться обычному маляру. Ведь если шар большой, а краски мало, то возникает вопрос – хватит ли ему этой смеси, чтобы покрасить весь объект. И это далеко не единственный бытовой случай, где может пригодиться формула.
Формула вычисления объёма может пригодиться и строительной бригаде, что делает ремонт. И неважно, какой это объект – промышленное здание, небольшой дом или обычная квартира. Этим и отличаются профессионалы – они умеют применять свои знания на практике.
Но как быть, если не представляется возможным измерить объект? Такой вопрос может возникнуть в случае огромных размеров объекта или его недосягаемости. В этом случае могут помочь электронные технологии, в основе работы которых лежит сканирование пространства определёнными частотами и лазерами. С современными технологиями необязательно знать все формулы наизусть. Достаточно иметь подключение к интернету и зайти на любой онлайн-калькулятор.
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x – x 0) 2 + ( y – y 0) 2 + ( z – z 0) 2 = R 2
3. Параметрическое уравнение сферы с центром в точке ( x 0, y 0, z 0):
x = x 0 + R · sin θ · cos φ y = y 0 + R · sin θ · sin φ z = z 0 + R · cos θ
где θ ϵ [0, π ], φ ϵ [0,2 π ].
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда:
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
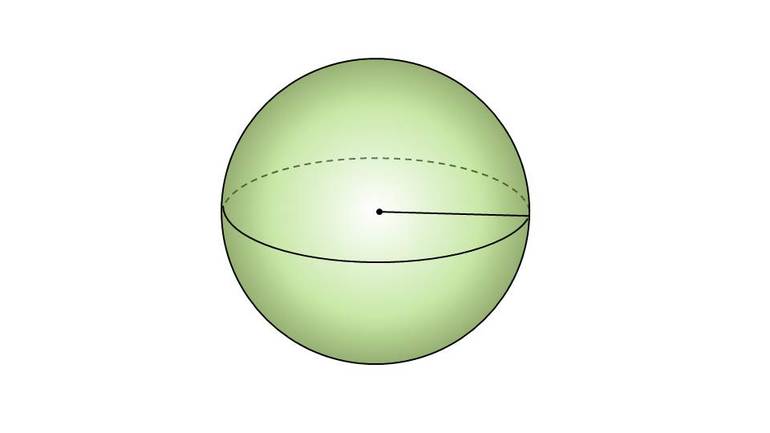
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Трактовка значений
Введите радиус сферы:
Сфера – геометрическое тело, ограниченное поверхностью, все точки которой находятся на равном расстоянии от центра. Это расстояние называется радиусом шара.
Через диаметр
Как известно, диаметр шара равен двум его радиусам: d = 2R. Следовательно, рассчитать площадь фигуры поверхности можно, используя такой вид формулы:
S = 4 π (d/2) 2
Терминология и сферическая геометрия
Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).
Круги на сфере, проходящие параллельно экватору, называются линиями широты. Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).
Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.
Площадь сферы — формулы и примеры вычислений
Идеально круглый геометрический объект, который определяется как множество всех точек, равноудалённых от одной заданной, называется сфера. Площадь ее поверхности, в сравнении с другими трёхмерными телами, имеет наибольший объём. По сути, это шар, имеющий однородную форму, то есть как ни повернуть, он всегда будет выглядеть одинаково.
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.
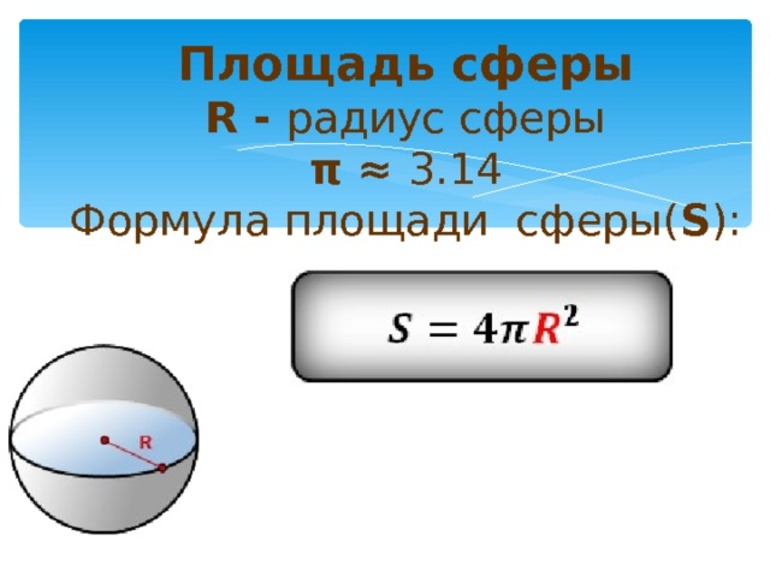
Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
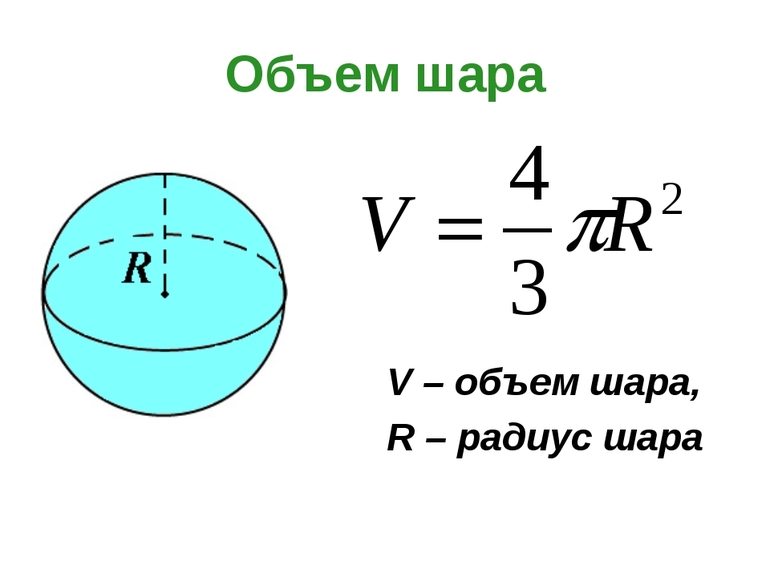
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Сектор сферы — это слой между двумя правильными круговыми конусами, имеющими общую вершину в центре шара и общую ось.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Терминология и сферическая геометрия
Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).
Круги на сфере, проходящие параллельно экватору, называются линиями широты. Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).
Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.
Одиннадцать свойств
В своей книге «Геометрия и воображение» Дэвид Гилберт и Стефан Кон-Фоссен описывают свойства сферы и обсуждают, однозначны ли такие характеристики. Несколько пунктов справедливы и для плоскости, которую можно представить как шар с бесконечным радиусом:
Сфера превращается в себя трёхпараметрическим семейством жёстких движений. Любое вращение вокруг линии, проходящей через начало координат, может быть выражено как комбинация вращений вокруг трёхкоординатной оси.
О шаре и цилиндре
Так называлась работа, опубликованная античным математиком Архимедом. Она вышла в двух томах в 225 году до н. э. Он был первым, кто сделал полный и подробный трактат по основам вычисления площади поверхности сферы, объёма шара и аналогичных значений для таких элементов, как цилиндр. Результатами его деятельности пользуются до сих пор.
Архимед особенно гордился формулой объёма шара, где он доказал, что эта величина составляет две трети объёма описанного цилиндра. Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью.
Аргумент, который Архимед использовал для доказательства формулы V шара, был довольно сложным и сильно вовлечён в его геометрию. Поэтому во многих современных учебниках используется упрощённая версия, основанная на концепции предела, которого, конечно, не было в античные времена. Великий математик создавал в сфере усечённый конус путём построения и вращения геометрических фигур, и только после этого он определил объём.
Сейчас кажется, что он специально выбирал такие оригинальные методы. Однако это был всего лишь лучший из тех, которые были ему доступны в греческой математике. Его основные работы были вновь открыты в XX веке. Например, Метод механических теорем, как он назывался в трактате автора.
Важные измерения
Радиус (обозначается r) — единственное необходимое измерение. Это расстояние от любой точки на поверхности сферы до её центра. Самый длинный отрезок, равный двум r, называется диаметром (d). Земля называется сфероидом, потому что она очень близка к шару, но не идеально круглая. Она немного вытянута на северном и южном полюсах.
Впервые вычислить площадь (S) поверхности шара удалось Архимеду. Именно он установил, что для того, чтобы найти S любого трёхмерного объекта, необходимо измерить его радиус. Для сферы получилась следующая формула: S = 4 * π * r ². Для того чтобы понять, как это работает, следует рассмотреть пример. Известно, что радиус детского мяча 10 см. Остаётся ещё одна неизвестная — число π. Это математическая константа, которая выражает отношение длины окружности к её диаметру и равна примерно 3,14. Далее, следует подставить цифры в уравнение:
Таким образом, можно найти площадь сферы через её радиус по формуле, полученной ещё в античности. Ещё одна важная характеристика — это объём (V) фигуры. Он вычисляется следующим образом: V = (4/3) * π * r³. Если придерживаться условий задачи, то V мяча = (4/3) * 3,14 * 10³ равен ≈ 4187 см ³. Сейчас можно избежать длительных расчётов, если нужно узнать площадь сферы, онлайн-калькуляторы — сервисы, которые очень в этом помогают.
Сектор сферы — это слой между двумя правильными круговыми конусами, имеющими общую вершину в центре шара и общую ось.
Надо сказать, что внутренний конус может иметь основание с нулевым радиусом. Формула, по которой определяют площадь сектора, следующая: S = 2 * π * r * h, где h — высота. К слову, эта же формула применима, если необходимо найти S части шара, отрезанной плоскостью, то есть полусферы. Такая же формула применяется при нахождении S сегмента (часть между двумя параллельными плоскостями) и зоны сферы (изогнутая поверхность сферического сегмента).
Терминология и сферическая геометрия
Окружность на шаре, которая имеет тот же центр и радиус, что и сама фигура, а следовательно, делит её на две части, называется большим кругом. Если конкретную (произвольную) точку этого геометрического тела обозначить как его северный полюс, то соответствующая антиподальная точка будет южным полюсом. А большой круг станет экватором и будет равноудалённым от них. Если он будет проходить через два полюса, тогда это уже линии долготы (меридианы).
Круги на сфере, проходящие параллельно экватору, называются линиями широты. Все эти термины используются для приблизительно сфероидальных астрономических тел. Любая плоскость, которая включает в себя центр шара, делит его на два равных полушария (полусферы).
Многие теоремы из классической геометрии верны и для сферической, но отнюдь не все, потому что сфера не удовлетворяет некоторым аксиомам, например, постулату параллельности. Такая же ситуация складывается и в тригонометрии — отличия есть во многих отношениях. Например, сумма внутренних углов сферического треугольника всегда превышает 180 градусов. Помимо этого, две таких одинаковых фигуры будут конгруэнтными.
Одиннадцать свойств
В своей книге «Геометрия и воображение» Дэвид Гилберт и Стефан Кон-Фоссен описывают свойства сферы и обсуждают, однозначны ли такие характеристики. Несколько пунктов справедливы и для плоскости, которую можно представить как шар с бесконечным радиусом:
Сфера превращается в себя трёхпараметрическим семейством жёстких движений. Любое вращение вокруг линии, проходящей через начало координат, может быть выражено как комбинация вращений вокруг трёхкоординатной оси.
О шаре и цилиндре
Так называлась работа, опубликованная античным математиком Архимедом. Она вышла в двух томах в 225 году до н. э. Он был первым, кто сделал полный и подробный трактат по основам вычисления площади поверхности сферы, объёма шара и аналогичных значений для таких элементов, как цилиндр. Результатами его деятельности пользуются до сих пор.
Архимед особенно гордился формулой объёма шара, где он доказал, что эта величина составляет две трети объёма описанного цилиндра. Он даже попросил сделать чертёж этих предметов на своей надгробной плите. Позже римский философ Цицерон обнаружил такую гробницу, к сожалению, сильно заросшую окружающей растительностью.
Аргумент, который Архимед использовал для доказательства формулы V шара, был довольно сложным и сильно вовлечён в его геометрию. Поэтому во многих современных учебниках используется упрощённая версия, основанная на концепции предела, которого, конечно, не было в античные времена. Великий математик создавал в сфере усечённый конус путём построения и вращения геометрических фигур, и только после этого он определил объём.
Сейчас кажется, что он специально выбирал такие оригинальные методы. Однако это был всего лишь лучший из тех, которые были ему доступны в греческой математике. Его основные работы были вновь открыты в XX веке. Например, Метод механических теорем, как он назывался в трактате автора.
Что такое шар (сфера): определение, свойства, формулы
В публикации мы рассмотрим определение и основные свойства шара и сферы, а также формулы, с помощью которых можно найти площадь поверхности и объем данных геометрических фигур.
Определение шара и сферы
Шар – это совокупность всех точек в трехмерном пространстве, которые находятся на расстоянии не больше заданного от точки, называемой центром шара (на рисунке ниже – это точка O). Другими словами, это совокупность точек, ограниченных сферой.
Шар образуется путем вращения круга вокруг своего диаметра (оси) на 180° или полукруга – на 360°.
Сфера – это поверхность шара. Образуется путем вращения окружности вокруг своего диаметра на 180° или полуокружности – на 360°.
Различают два вида шаров:
Радиус шара (сферы) – расстояние между центром и точками, лежащими на его поверхности. На рисунке выше обозначен буквой R.
Диаметр шара (сферы) – отрезок, проходящий через центр шара и соединяющие две противоположные точки на его поверхности. Совпадает с осью шара, обычно обозначается буквой d.
Полюсы шара (сферы) – точки A и B, расположенные на концах его диаметра.
Свойства шара и сферы
Свойство 1
Любое сечение шара плоскостью является кругом.
Свойство 2
Любое сечение сферы плоскостью является окружностью.
Свойство 3
Все точки сферы равноудалены от ее центра.
Свойство 4
Сфера имеет самый большой объем среди всех фигур в пространстве, имеющих одинаковую площадь поверхности.
Свойство 5
Через две любые диаметрально противоположные точки (максимально отдаленные друг от друга точки на окружности) можно провести неограниченное количество кругов для шара или окружностей для сфер радиусом, равным радиусу шара/сферы.
Примечание: если точки не диаметрально противоположны, то провести можно только один круг (окружность).
Части шара
Сегмент шара – это часть шара, отсекаемая плоскостью. Иногда называется шаровым сегментом. На рисунке ниже окрашен в зеленый цвет.
Срез шара – часть шара между двумя параллельными плоскостями, пересекающими его. Также может называться шаровым слоем. На рисунке ниже закрашен желтым.
Сектор шара – состоит из шарового сегмента и конуса, вершина которого находится центре шара, а основание совпадает с основанием сегмента. На рисунке ниже сектор залит оранжевым.
Формулы для шара/сферы
В формулах ниже используется как радиус (R), так и диаметр фигур (d). Число π в расчетах обычно округляется до двух знаков после запятой и приблизительно равняется 3,14.
Геометрические фигуры. Шар, сфера.
Понятие шара в метрическом пространстве естественным образом обобщает понятие шара в евклидовой геометрии.
Радиус AO и диаметр AB находят тем же способом, что и для окружности.
Сфера является поверхностью (границей) шара с центром и радиусом, как у сферы.
Шар — это тело правильно геометрической формы, ограниченное поверхностью шара. Шар возможно получить, методом вращения полукруга/круга около диаметра.
Любое плоское сечение шара является кругом. Чем ближе секущая плоскость к центру шара, тем радиус круга становится больше. Самый большой круг оказывается при прохождении плоскости через центр O. Этот круг разделяет шар на две равные части и он называется большим кругом. Радиус большого круга равен радиусу шара.
Меридианы шара (сферы).
Сквозь 2 точки шара, которые лежат на концах общего диаметра, возможно провести бесконечное число больших кругов — меридианов. Через 2 точки, которые не на концах общего диаметра шара возможно провести всего лишь 1 большой круг.
Основные геометрические формулы шара (сферы).
Площадь поверхности S и объём V шара радиуса r, диаметра d можно определить по формулам:
Определения, связанные с понятием шара.
Предположим, дано метрическое пространство (X, ρ). Значит:
Замкнутый шар с центром в x0 и радиусом r можно выразить так:
Свойства шара.
Sцил и Vцил – полная поверхность и объём описанного цилиндра вокруг шара.
| Части шара. |
 |  |