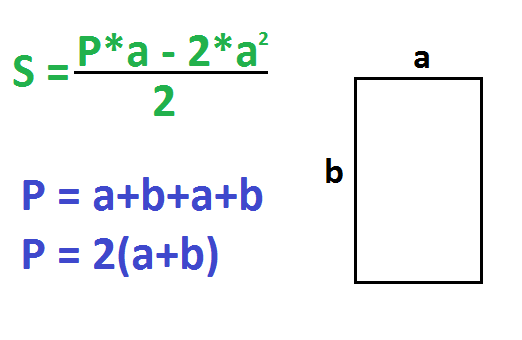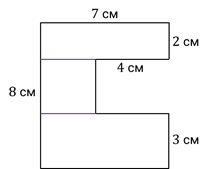Что такое площадь в математике 4 класс прямоугольник

Как найти площадь прямоугольника – 9 способов с формулами и примерами

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

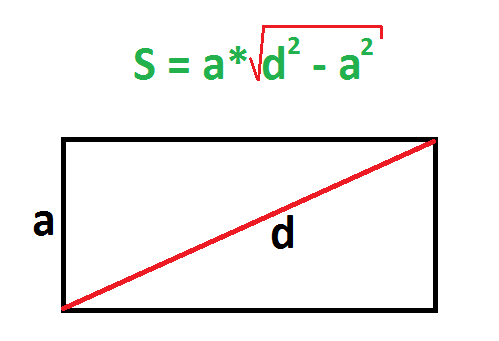
По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

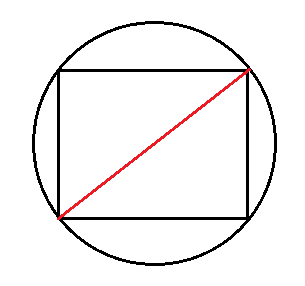
По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

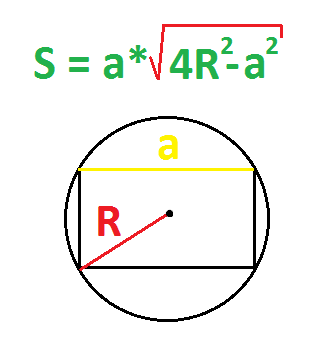
По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.

По стороне и периметру – 2 способ

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

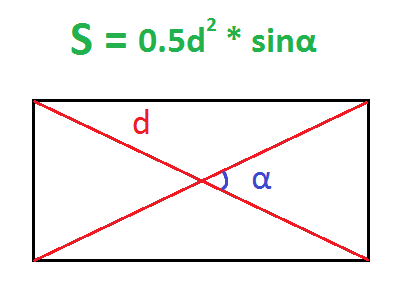
По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

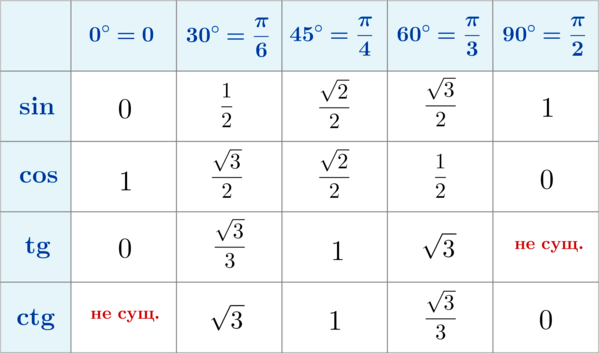
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

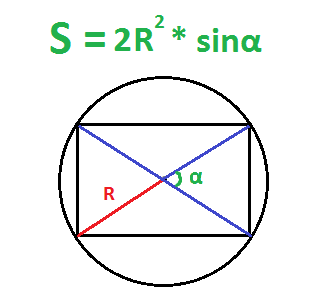
По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

По радиусу описанной окружности и углу между диагоналями – второй способ

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

Источник

Задачи на нахождение периметра и площади для 4 класса с ответами

Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:

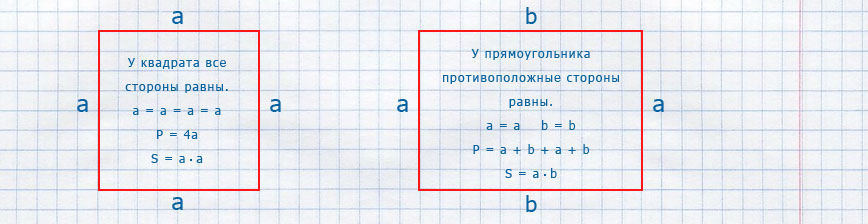
Формулы площади и периметра для квадрата

P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата

Формулы площади и периметра для прямоугольника

P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника

Примеры решения задач разной сложности на нахождение периметра и площади

Задача 1

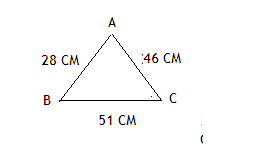
Каков периметр треугольника ABC?

Ответ: периметр треугольника равен 125 см.

Задача 2

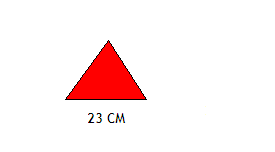
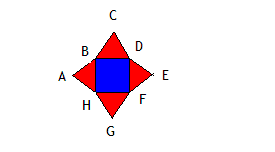
Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?

Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.

Задача 3

Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?

Задача 4

У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?

Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.

Задача 5

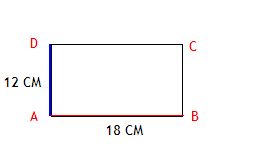
В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?

Ответ: Периметр прямоугольника равен 60 см.

Задача 6

Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?

Ответ: Площадь прямоугольника 56 м².

Задача 7

Площадь витрины квадратной формы 64м². Узнай ее периметр.

Ответ: Периметр витрины равен 32 м.

Задача 8

Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.

Ответ: Площадь прямоугольника равна 630 см².

Задача 9

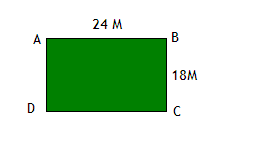
Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?

Задача 10

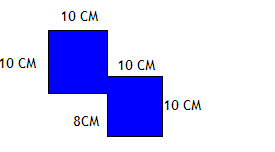
Каков периметр синей фигуры?

Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.

Ответ: Длина второго участка 40 м.

Задача 12

Найди периметр квадрата со стороной 8 см.

Ответ: Периметр квадрата 32 см.

Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.

Решение:

120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)

Ответ: Периметр бассейна 46 метров

Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.

Решение:

8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)

Ответ: Периметр прямоугольника 16 см.

Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?

Решение:

5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)

Ответ: Ученик ошибся на 3 см²

Ответ: Ширина другого участка 24 м.

У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?

Ответ: Площадь квадрата больше на 4 см.

Задача 20

Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.

Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.

У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.

Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.

Задача 22

Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?

1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36

Ответ: Незабудками засажено 36 м².

Задача 23

Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?

1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18

Ответ: Площадь прямоугольника 18 м².

Задача 24

Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?

1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см

Ответ: Периметр стола 280 см.

Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?

1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75

Ответ: Площадь прямоугольника 75 см².

Площадь квадрата 49 кВ дм. Узнайте его периметр.

1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)

Ответ: Периметр квадрата равен 28 дм.

Задача 27

Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.

1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32

Ответ: Площадь окна равна 32 м².

1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152

Ответ: Капустой засадили 1152 м².

Найди периметр квадрата со стороной 16 см.

Ответ: Периметр квадрата 64 см.

Задача 30

Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.

Ответ: Длина прямоугольника 13 см.

Задача 31

Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.

Ответ: Ширина прямоугольника 5 см.

Задача 32

Периметр квадрата 24 см. Найди его площадь.

24 : 4 = 6 (см)
6 · 6 = 36 (см²)

Ответ: Площадь квадрата 36 см².

Задача 33

Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.

Ответ: Площадь прямоугольника 56 см².

Задача 34

Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?

40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)

Ответ: Периметр прямоугольника 28 см.

Задача 35

Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.

Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.

У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).

Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)

Ответ: Площадь всех граней куба равна 24 см².

Задача 36

Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

Ответ: Площадь получившейся фигуры равна 44.

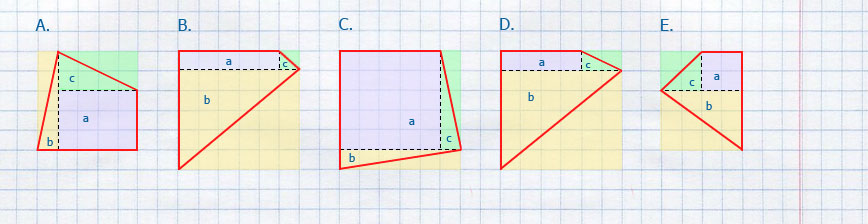
Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².

Задача 38

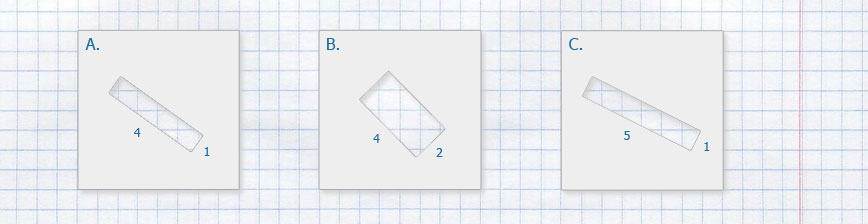
Найдите площади и периметры фигурок. Сделайте вывод.

Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²

Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.

Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.

Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.

Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.

Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.

Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.

Ответ: Периметр красной фигуры равен 27 см.

Задача 40

Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?

Ответ: Периметр равен 36 см.

Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?

Задача 42

Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.

Ответ: Периметр прямоугольника равен 24 см.

Задача 43

Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?

Ответ: Расстояние пройденное улиткой будет равно 28 см.

Задача 44

В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?

Задача 45

Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?

Источник

Задачи на нахождение площади сложных фигур

Урок 21. Математика и игры 3–4 классы

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Задачи на нахождение площади сложных фигур»

Давайте вспомним, как найти площадь прямоугольника. Чтобы найти площадь прямоугольника, надо длину умножить на ширину.

Вот формула для нахождения площади прямоугольника:

В этой формуле латинской буквой S обозначается площадь, буквами a и b – стороны прямоугольника.

Выполним задание, в котором надо найти площадь прямоугольника со сторонами 5 см и 3 см.

Решение. Итак, чтобы найти площадь прямоугольника, надо его длину умножить на ширину.

Произведение чисел 5 и 3 равно 15. Значит, площадь прямоугольника равна 15 квадратным сантиметрам. Не забудьте, что площадь измеряется именно в квадратных единицах. В данной задаче это квадратные сантиметры. Также важно помнить, что длина и ширина должны быть выражены в одинаковых единицах длины.

Теперь давайте найдём площадь квадрата со стороной 4 см.

Решение. У этого квадрата каждая сторона равна 4 см, поэтому умножим 4 на 4 и получится, что площадь квадрата равна 16 квадратным сантиметрам.

Ну а сейчас перейдём к решению задач, в которых нам надо будет найти площадь сложных фигур.

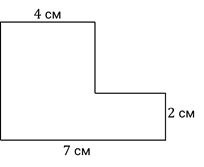
Найдите площадь фигуры, изображённой на рисунке.

Эта фигура не является ни прямоугольником, ни квадратом. Но мы можем разделить эту фигуру на два прямоугольника, например, вот таким образом.

А площади прямоугольников мы легко можем найти с помощью известной формулы.

Напомним, что противоположные стороны прямоугольника равны.

Итак, стороны первого прямоугольника равны 5 см и 4 см.

5 · 4 = 20 (см 2 ) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

Ширина этого прямоугольника равна 2 см.

7 – 4 = 3 (см) – длина второго прямоугольника

3 · 2 = 6 (см 2 ) – площадь второго прямоугольника

Мы нашли площади прямоугольников, из которых состоит сложная фигура. Чтобы найти площадь этой фигуры, надо сложить найденные площади.

20 + 6 = 26 (см 2 ) – площадь сложной фигуры

Площадь этой сложной фигуры найти другим способом. Можно разделить её на два прямоугольника вот таким образом.

Найдём площадь первого прямоугольника.

Одна его сторона равна 4 см.

5 – 2 = 3 (см) – длина стороны первого прямоугольника

4 · 3 = 12 (см 2 ) – площадь первого прямоугольника

Теперь найдём площадь второго прямоугольника.

7 · 2 = 14 (см 2 ) – площадь второго прямоугольника

12 + 14 = 26 (см 2 ) – площадь сложной фигуры

Решим следующую задачу.

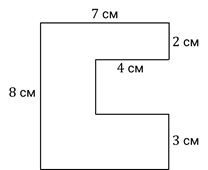
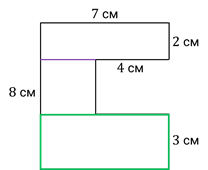
Найдём площадь ещё одной фигуры, изображённой на рисунке.

Чтобы найти площадь этой фигуры, тоже разделим её на простые фигуры. Сделаем это вот таким образом.

Получилось 3 прямоугольника.

Найдём площадь первого прямоугольника.

7 · 2 = 14 (см 2 ) – площадь первого прямоугольника

Найдём площадь второго прямоугольника.

7 – 4 = 3 (см) – длина одной стороны второго прямоугольника

8 – 2 – 3 = 3 (см) – длина другой стороны второго прямоугольника

Получается, что это квадрат, так как длина всех его сторон равна 3 см.

3 · 3 = 9 (см 2 ) – площадь квадрата

И найдём площадь последнего прямоугольника.

Его ширина равна 3 см. Длина равна 7 см.

3 · 7 = 21 (см 2 ) – площадь третьего прямоугольника

Таким образом, мы нашли площади всех трёх фигур, на которые разделили данную сложную фигуру. Площадь этой сложной фигуры найдём как сумму площадей трёх фигур.

14 + 9 + 21 = 44 (см 2 ) – площадь сложной фигуры

Ответ: площадь фигуры, изображённой на рисунке, равна 44 см 2

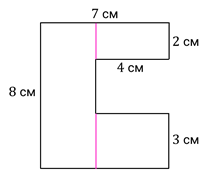
Отметим, что площадь этой фигуры можно было бы найти, разделив её на простые фигуры и вот таким образом:

И решим ещё одну задачу.

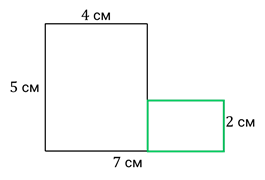
Найдите площадь незаштрихованной фигуры.

На рисунке изображён прямоугольник со сторонами 9 см и 5 см. Внутри этого прямоугольника расположен ещё один прямоугольник со сторонами 5 см и 3 см. Давайте найдём площадь каждого из них.

9 · 5 = 45 (см 2 ) – площадь большего прямоугольника

5 · 3 = 15 (см 2 ) – площадь меньшего прямоугольника

А как найти площадь незаштрихованной фигуры? Площадь этой фигуры найдём, если из площади большего прямоугольника вычтем площадь меньшего прямоугольника.

45 – 15 = 30 (см 2 ) – площадь незаштрихованной фигуры

Источник

Урок математики, 4 класс. «Площадь прямоугольника»

Выбранный для просмотра документ Конспект урока.docx

Урок математики в 4 «Б» классе

учитель Малиновская Н. В.

Тема. Площадь прямоугольника.

Место урока в изучаемой теме: 4-ый урок в теме «Единицы измерения площади».

Цель. Знакомство с формулой площади прямоугольника.

уточнить значение понятия «площадь» фигуры и его отличие от понятия «периметр»;

актуализировать знание учащихся единиц измерения площади и их соотношения, умение выражать значение площади в единицах других наименований;

познакомить с формулой площади прямоугольника;

способствовать формированию способности к интеллектуальной деятельности (логического, знаково-символического мышления), пространственного воображения, математической речи;

вырабатывать умение выбирать аргументации, определять истинность и ложность суждений, строить суждения;

развивать стремление использовать математические знания в повседневной жизни, через практико-ориентированные задания.

Создать условия для формирование коммуникативных умений через организацию групповой формы работы.

Планируемый результат: готовность учащихся на завершающем этапе урока выполнить проверочный тест по теме «Единицы измерения площади».

Тип урока. Урок новых знаний.

Оборудование и обеспечение урока: распечатка урока из «Рабочей тетради» Г. Л. Муравьёвой и др.; палетки, геометрические фигуры – весёлые и грустные; карточки мини-теста и проверочного теста.

I . Организационно-мотивационный этап. Весёлые и грустные геометрические фигуры.

II . Чистописание. На материале домашнего задания.

III . Проверка домашнего задания. Актуализация знаний.

Перевод одних единиц измерения площади в другие.

Проверка решения задачи в группах

для глаз (зелёная точка)

статическая (изображение ГФ в парах)

V . Постановка учебной задачи. Актуализация субъективного опыта учащихся. На базе домашней задачи.

VI . Создание проблемной ситуации. Актуализация ранее изученных (3-4 кл.) способов определения площади.

VII . Определение нового способа вычисления площади. Работа с учебником. Знакомство с понятием «формула», с формулой площади прямоугольника.

Применение полученных знаний и способов действия. ( Работа в парах)

VIII . Создание ситуации успеха. Домашнее задание (дифференцированное по уровням сложности) .

IX . Проверочный тест. Взаимоконтроль (выбор партнёра по желанию). Оценивание.

X . Рефлексия. Подтверждение достижения цели урока. Определение практической значимости урока для каждого учащегося.

I . Организационно-мотивационный этап.

— На любом уроке, в любом деле нам необходимо внимание, собранность, умение логически мыслить и гибкость ума. А ещё –позитивный настрой на результат своего труда. Именно поэтому предлагаю посмотреть на доску: что это? (Геометрические фигуры)

-Что в них необычного? ( На них изображены лица)

-На какие две группы по этому признаку их можно разделить? ( Лица веселые и грустные )

— Посмотрите внимательно, запомните. Закройте глаза. (Убираю грустные лица)

-Что изменилось? ( Остались фигуры веселые, радостные)

-Какое настроение они дарят?

-Я тоже желаю вам хорошего рабочего настроения! Пусть на этом уроке у вас всё получится, и вы сможете проявить себя наилучшим образом!

II . Чистописание. (Написание этих цифр получается хуже всего)

9 – 90 800 – 8 600 – 6 7 – 7000 20 000 – 20 4 – 40 000

III . Проверка домашнего задания. Актуализация знаний.

Внимательно всмотритесь в эту запись и подумайте, где вы могли встречаться уже с такими же парами чисел? (В Д/З) Что нужно было сделать? (Урок 38 рабочей тетради).

— Какие равенства оказались неверными? (Подчеркнуть пары)

Взаимоконтроль, взаимооценка в парах .

— Какие знания и умения вам понадобились, чтобы выполнить это задание без ошибок?

— Обязательно ли всю таблицу перевода одних единиц измерения площади в другие зазубривать? (Это нерационально. Нужно лишь твёрдо знать соотношение единиц длины, а площадь – легко потом вычислить!)

— Кому ещё нужно время и тренировки, чтобы твёрдо усвоить соотношения единиц площади?

— Оценки в журнал ставим по желанию, т.к. перевод единиц площади сложен, а мы лишь 1 урок тренировались.

Проверим решение задачи. Напомните условие.

— Какой из двух планов выбрали? Аргументируйте свой выбор?

— Проверьте решение задачи в группах. Взаимопроверка и взаимооценка.

— У меня получилось так: под свёклой занято 80 м² огорода. Права ли я? (Нет, это оставшаяся часть. Надо 80 : 4, т.к. свёкла занимает ¼ часть)

— На прошлом уроке мы ставили перед собой цель – научиться устанавливать соотношения между различными единицами площади и закрепить умение решать задачи, связанные с площадью. Цель, по-вашему, достигнута? Молодцы, вам удалось продемонстрировать неплохие знания темы. Можем двигаться вперёд!

статическая. Посмотрите на ГФ на доске. Постройте некоторые из них, используя свои руки и руки соседа.

V . Постановка учебной задачи. Актуализация субъективного опыта учащихся.

— Сегодня мы расширим и углубим знания о площади фигур. Научимся определять площадь прямоугольника по-новому. Заодно узнаем, зачем надо уметь определять площадь. К концу урока вы сможете выполнить проверочный тест по теме урока.

— Вернёмся к домашней задаче. Посмотрите на план огорода. (План 1 )

— Что мы сейчас находили? (Периметр) Докажите.

— Совсем недавно внук, Володя, сказал бабуле, что её огород занимает большую площадь, что слишком много сил они с дедом тратят на его обработку, и надо бы уменьщить эту самую площадь огорода, заодно и экономия будет: не надо так много сетки покупать! Что имелл ввиду Володя – что такое площадь?

— Чем площадь отличается от периметра?

VI . Создание проблемной ситуации.

— (Показываю палетки) Что это такое? Для чего? Когда использовали?

— Предлагаю бабушкин огород измерить палеткой. (Нерационально. ) Тогда, на глаз определить. Мы в 3 классе учились сравнивать площади фигур наложением. Подойдёт?

VII . Определение нового способа вычисления площади. Работа с учебником.

(Стр. 76) – анализ теории;

— Итак, мы познакомились с правилом вычисления площади прямоугольника в виде буквенного равенства. Это равенство в математике называют ФОРМУЛОЙ. Данную формулу можно использовать для вычисления площади ЛЮБОГО ПРЯМОУГОЛЬНИКА!

— Как вы думаете, удобнее узнавать площадь прямоугольника с помощью мерок или пользуясь формулой? Почему?

Запись на доске и в тетрадях 3 · 1 = 3 см² 3 · 2 = 6 см² 2 · 1 = 2 см²

Вернёмся к бабушкиному огороду. Как определить его площадь?

— Размеры огорода предположила я. А какими ещё могут быть стороны огорода, чтобы его площадь была 120 м²? (3 м и 40 м; 6 м и 20 м)

— С какой целью мы выполняли это задание? В жизни мы очень часто сталкиваемся с такими ситуациями, когда приходится определять площадь. Можете привести примеры? ( Допустим, чтобы покрасить пол, мы должны знать, сколько краски понадобится. А для этого нужно вычислить площадь. Ламинат или линолеум положить. Обои поклеить. Вагонкой или гипсокартоном обшить стены. ) В строительстве, на дачном участке, в ремонтных работах.

VIII . Создание ситуации успеха. Домашнее задание (дифференцированное по уровням сложности) .

– В будущем мы все должны научиться решать задачи на нахождение периметра и площади только на 10! Дома у вас будет возможность потренироваться в вычислении площади, выполнив №2 (стр. 77), а также не забыть приёмы вычислений с многозначными числами: №1.

– Кто заинтересован в более прочных знаниях и любит выполнять задания поинтересней и посложней, выполнит задания из рабочей тетради (стр. 39)

IX . Проверочный тест. Каждый сейчас определит для себя: научился он вычислять площадь прямоугольника или нет.

Найди единицы измерения площади

Найди верное определение площади:

А) Площадь фигуры – это величина, которая показывает, чему равна сумма длин всех сторон фигуры.

Б) Площадь фигуры – это величина, которая показывает, сколько места занимает фигура на плоскости.

В) Площадь фигуры – это величина, которая показывает, чему равна масса фигуры.

Выбери верное высказывание. Чтобы найти площадь прямоугольника, надо:

А К длине прибавить ширину.

Б) Длину и ширину умножить на 2 и результаты сложить.

В) Длину умножить на ширину.

Выбери формулу вычисления площади прямоугольника:

Длина прямоугольника – 5 см, ширина – 4 см. Чему равна его площадь?

А) 9 см² Б) 18 см² В) 20 см²

Ключ к проверке: 1 Б, 2 Б, 3 В, 4 А, 5 В. Взаимоконтроль (выбор партнёра по желанию)

Оценку получают те, кто ещё не получил на этом уроке.

– Вернёмся к началу урока: какую цель ставили? Достигли?

– Какое задание показалось наиболее трудным? А какое наиболее интересным.

Всегда напоминаю вам: уроки математики учат нас знаниям, навыкам, что нам может пригодиться и найти применение в нашей жизни.

Источник