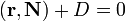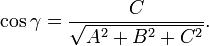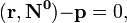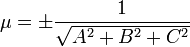Что такое плоскость определение 5 класс
Плоскость. Прямая. Луч
Урок 4. Математика 5 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Плоскость. Прямая. Луч»
На этом уроке мы познакомимся с понятиями «отрезок», «прямая», «луч» и «плоскость». Рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.
На прошлом уроке мы разобрались, как строить отрезок. Мы уже знаем, что отрезок – это прямая линия, ограниченная двумя точками.
Давайте начертим отрезок MN. Если продлить этот отрезок неограниченно за точку N, то мы получим новую фигуру, которая называется луч. У нас получился луч MN.
Точку М называют началом луча.
Если бы мы продлевали отрезок MN неограниченно за точку М, то у нас бы получился луч NМ, у которого точка N – начало луча.
Заметьте: обозначается луч большими заглавными буквами латинского алфавита, первой буквой записывают его начало, а затем букву, обозначающую какую-либо другую точку луча.
Обратите внимание, что луч имеет начало, но не имеет конца, т. е. он бесконечен в одну сторону.
Для того чтобы представить луч в окружающей среде, достаточно сфотографировать след от самолёта в безоблачном небе, где сам самолёт – это начальная точка, а след, оставленный на небе, – это прямая линия, которая бесконечна.
Либо солнечный луч, где начальная точка – это солнце, а конечной точки нет.
Если отрезок MN неограниченно продлевать в обе стороны – как за точку М, так и за точку N, то у нас получится фигура, которая называется прямой.
На рисунке у нас получилась прямая MN, также её можно назвать и прямая NМ. Как кому больше нравится!
Заметьте, что прямая не имеет ни начала, ни конца.
Любая точка прямой разделяет её на 2 луча.
В нашем случае точка О разделяет прямую MN на луч ОМ и луч ОN. Лучи, на которые точка разбивает прямую, называют дополнительными друг другу.
Представление о прямой можно получить, если сложить лист бумаги (линия, которая получилась при сгибе, и будет прямой) или туго натянуть верёвку.
В математике прямая представляется идеально ровной и бесконечной в обе стороны.
Прямую можно обозначить двумя вариантами.
1-й вариант: двумя заглавными буквами латинского алфавита, например MN. В таком случае говорят: «Прямая MN».
2-й вариант: прямую обозначают одной малой буквой, например m, и говорят: «Прямая m».
Давайте попробуем провести ещё одну прямую через эти же две точки.
У нас это не получится. Через любые две точки можно провести только одну прямую!
Точки, отрезки, лучи и прямые располагаются в плоскости. Примеры плоскостей в жизни мы встречаем каждый день. Представление о плоскости дают поверхности стола, оконного стекла или замёрзшего водоёма.
Только эти поверхности имеют границы, а плоскость в математике безгранична во всех направлениях. Мы рисуем фигуры на «кусках» плоскости, например в тетрадном листе или на школьной доске.
Теперь давайте рассмотрим расположение точек, отрезков, прямых и лучей в плоскости.
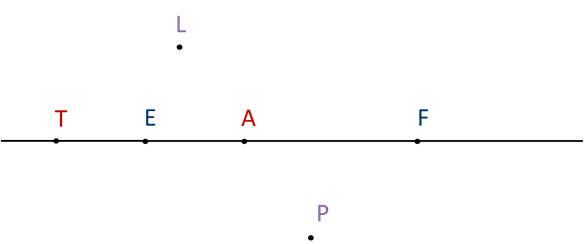
На рисунке изображены прямая EF и точки А, L, P и T. Точки А, E, F лежат на отрезке EF, а точки L, P, T не лежат на этом отрезке. Посмотрите, как это записывается.
Точки А, E, F лежат на луче EF, а точки А, E, F, Т лежат на луче FЕ. Посмотрите запись этих утверждений.
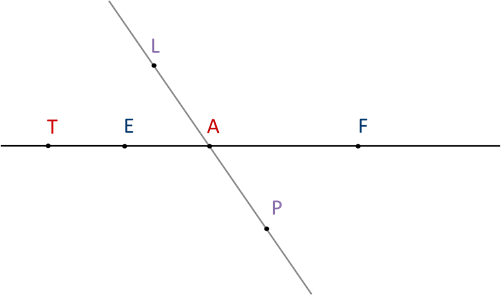
Точки А, E, F, Т лежат на прямой EF, а точки А, P, L – на прямой PL.
Обозначается это так:
Точка А лежит между точками Е и F. Точка L не лежит между точками Е и F, она находится вне отрезка EF. Точка Е лежит между точками А и Т, а точка А – между точками P и L.
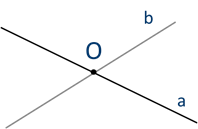
На следующем рисунке изображены прямая a и прямая b.
Если две прямые имеют одну общую точку, то говорят, что они пересекаются в этой точке. В нашем примере прямые а и b пересекаются в точке О. Точка О делит каждую прямую на две части. Точка О – точка пересечения прямых.
Посмотрите на взаимное расположение прямых m и n:
Они не имеют общих точек. Если прямые не имеют общих точек, то говорят, что они параллельны.
· Луч имеет начало, но не имеет конца.
Итак, на уроке мы с вами разобрались в отличиях понятий «отрезок», «прямая», «луч». Научились их строить. Узнали, что такое плоскость, а также рассмотрели расположение точек, отрезков, прямых и лучей в плоскости.
Плоскость (в математике)
Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Уравнение плоскости впервые встречается у А. К. Клеро (1731), уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818), нормальное уравнение ввёл Л. О. Гессе (1861).
Содержание
Некоторые характеристические свойства плоскости
Аналогично отрезку и интервалу, плоскость не включающую крайние точки можно назвать интервальной плоскостью или открытой плоскостью.
Уравнения плоскоcти
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
где A,B,C и D — постоянные, причём A,B и C одновременно не равны нулю; в векторной форме:
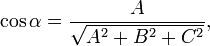
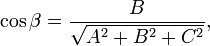
(смешанное произведение векторов), иначе
где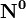 
— единичный вектор, p — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
(знаки μ и D противоположны).
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между параллельными плоскостями
Связанные понятия
Если в векторной форме, то
где α и β — любые числа, не равные одновременно нулю.
Плоскости в четырёхмерном пространстве
Если в четырёхмерном пространстве две плоскости лежат в одной гиперплоскости, то они могут либо быть параллельными (в частности, совпадать), либо пересекаться по линии.
Если же две плоскости не лежат в одной гиперплоскости, то они либо не пересекаются (скрещиваются, подобно тому как в трёхмерном пространстве скрещиваются прямые), либо имеют ровно одну общую точку.
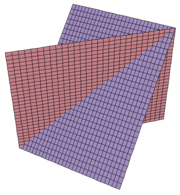
Пересечение двух плоскостей в точке (а не по линии, как в трёхмерном пространстве) можно проиллюстрировать следующим примером. Пусть дана система декартовых координат x y z t. Пусть две плоскости α и β проходят через начало координат, причём плоскость α содержит координатные прямые x и y, а плоскость β содержит координатные прямые z и t. Соответственно у всех точек плоскости α координаты z и t равны 0, а у всех точек плоскости β координаты x и y равны 0. Тогда очевидно, что единственная точка, которая может принадлежать обеим плоскостям — это точка (0,0,0,0).
Литература
Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
Полезное
Смотреть что такое «Плоскость (в математике)» в других словарях:
ПЛОСКОСТЬ — ПЛОСКОСТЬ, в математике плоская поверхность, такая, что любая прямая, соединяющая две ее точки, целиком принадлежит этой поверхности. Общее уравнение плоскости в трехмерной декартовой системе координат выглядит как ах+by+cz=d, где а, b, с и d… … Научно-технический энциклопедический словарь
Плоскость Минковского — В математике, плоскость Минковскогоe двумерное аффинное пространство снабжённое метрикой которая инвариантна относительно параллельных переносов. Названа в честь Минковского. Часто данное аффинное пространство ототожествляют с плоскостью R2.… … Википедия
Плоскость Лобачевского — Геометрия Лобачевского (гиперболическая геометрия) одна из неевклидовых геометрий, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на… … Википедия
Фокус (в математике) — Конические сечения: окружность, эллипс, парабола (плоскость сечения параллельна образующей конуса), гипербола. Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс,… … Википедия
соприкасающаяся плоскость — в точке M кривой l, плоскость, имеющая с l в точке М касание порядка п≥2. См. Соприкосновение,Кручение. * * * СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ в точке M кривой l, плоскость, имеющая с l в точке M касание порядка nі2. См.… … Энциклопедический словарь
Симметрия (в математике) — Симметрия (от греч. symmetria ‒ соразмерность) в математике, 1) симметрия (в узком смысле), или отражение (зеркальное) относительно плоскости a в пространстве (относительно прямой а на плоскости), ‒ преобразование пространства (плоскости), при… … Большая советская энциклопедия
Расстояние в математике — Метрическим пространством называется множество, в котором определено расстояние между любой парой элементов. Содержание 1 Формальное определение 2 Обозначения 3 Примеры … Википедия
Координаты в математике — величины, определяющие положение точки. В Декартовых прямоугольных К. положение точки определяется тремя расстояниями ее от трех взаимно перпендикулярных плоскостей; пересечения этих плоскостей представляют собой три прямые, выходящие из одной… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Координаты, в математике — величины, определяющие положение точки. В Декартовых прямоугольных К. положение точки определяется тремя расстояниями ее от трех взаимно перпендикулярных плоскостей; пересечения этих плоскостей представляют собой три прямые, выходящие из одной… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Плоскость (математика)
Плоскость (математика)
Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Уравнение плоскости впервые встречается у А. К. Клеро (1731), уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818), нормальное уравнение ввёл Л. О. Гессе (1861).
Содержание
Некоторые характеристические свойства плоскости
Аналогично отрезку и интервалу, плоскость не включающую крайние точки можно назвать интервальной плоскостью или открытой плоскостью.
Уравнения плоскоcти
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
где A,B,C и D — постоянные, причём A,B и C одновременно не равны нулю; в векторной форме:
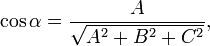
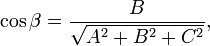
(смешанное произведение векторов), иначе
где 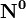— единичный вектор, p — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
(знаки μ и D противоположны).
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между параллельными плоскостями
Связанные понятия
Если в векторной форме, то
где α и β — любые числа, не равные одновременно нулю.
Плоскости в четырёхмерном пространстве
Если в четырёхмерном пространстве две плоскости лежат в одной гиперплоскости, то они могут либо быть параллельными (в частности, совпадать), либо пересекаться по линии.
Если же две плоскости не лежат в одной гиперплоскости, то они либо не пересекаются (скрещиваются, подобно тому как в трёхмерном пространстве скрещиваются прямые), либо имеют ровно одну общую точку.
Пересечение двух плоскостей в точке (а не по линии, как в трёхмерном пространстве) можно проиллюстрировать следующим примером. Пусть дана система декартовых координат x y z t. Пусть две плоскости α и β проходят через начало координат, причём плоскость α содержит координатные прямые x и y, а плоскость β содержит координатные прямые z и t. Соответственно у всех точек плоскости α координаты z и t равны 0, а у всех точек плоскости β координаты x и y равны 0. Тогда очевидно, что единственная точка, которая может принадлежать обеим плоскостям — это точка (0,0,0,0).
Литература
Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
Плоскость. Прямая. Луч
Содержание
Плоскость
Посмотрев вокруг, ты увидишь множество плоских вещей. Поверхность стола, лист бумаги, оконное стекло… А представьте себе, как будто эти поверхности не имеют конца и края, как будто они простираются за пределы Земли!
У математической плоскости нет границ. Она простирается бесконечно в любом направлении.
Прямая
Начертим отрезок АВ (рисунок 1). Он ограничен двумя точками. Теперь проведём по линейке линии таким образом, чтобы он продолжался в обе стороны (рисунок 2). У нас получилась прямая, на которой лежат точки А и В.
Конечно, мы можем приложить линейку и измерить ту линию на рисунке 2. Даже если мы будем чертить прямую не в тетрадке, а, скажем, на полу, и продолжать её в обе стороны до самых стен, её всё равно можно измерить. Но говоря о математической прямой, мы подразумеваем, что она не заканчивается и продолжается до бесконечности.
Прямая бесконечна. Она неограниченно продолжается в обе стороны.
Через любые две точки проходит только одна прямая.
Прямая обозначается двумя буквами, по тем точкам, через которые она проходит. На рисунке 2 – прямая АВ (можно также назвать ВА).
Теперь нарисуем две пересекающиеся прямые, АВ и СD. Та точка, в которой они пересекаются, общая для обеих прямых. Она делит каждую прямую на две части.
Луч
Начертим прямую и поставим на ней точку. Эта точка разделяет прямую на две части, каждую из них называют лучом.
У прямой нет ни начала, ни конца.
У луча тоже нет конца, но есть начало.
Представьте, что у вас в руке фонарик, и из него бьёт луч света. Фонарик и будет началом луча.
Для обозначения луча называют его начало и какую-нибудь из точек, лежащих на этом луче. Но переставлять буквы в названии уже нельзя, первой всегда будет идти буква, обозначающая точку-начало.
Например, луч на рисунке 6 называется ОА.
Лучи, на которые точка разбивает прямую, называются дополнительными друг другу.
Это как бы две половинки одной прямой.
Луч продолжается до бесконечности, и на нём можно поставить бесконечное число точек. Но всё равно будут точки, которые остаются вне этого луча. Представьте, что вы светите фонариком перед собой. То, что находится справа, слева, сзади, сверху – всё остаётся вне луча света.
На рисунке 7 показано, что точки В, С, D лежат на луче, а E и F – нет.
Значение слова «плоскость»
3. перен. Та или иная область, сфера, круг каких-л. явлений, отношений. Рассмотреть вопрос в различных плоскостях. □ Я старался только вывести г. Маркова из плоскости бесполезных исторических рассуждений и объяснить то, чего он не понял. Л. Толстой, Прогресс и определение образования. Основная плоскость, на которой можно было его особенно легко вести за собою, — это плоскость науки; здесь он сам охотно, любовно шел навстречу живым мыслям. Фурманов, Чапаев.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Пло́скость — это поверхность или фигура, образованная кинематическим движением образующей по направляющей, представляющей собой прямую (начертательная геометрия).
ПЛО’СКОСТЬ, и, мн. и, е́й, ж. 1. только ед. Отвлеч. сущ. к плоский (книжн.). П. груди. П. острот. 2. Поверхность, имеющая только два измерения, так что между любыми двумя точками ее можно провести прямую, к-рая целиком сольется с этой поверхностью (мат.). Пересечение плоскостей. || Предмет, представляющий собою такую поверхность, имеющий плоскую форму (спец.). Верхняя и нижняя п. биплана. 3. перен. Область, сфера, круг каких-н. явлений, отношений (книжн.). Эти вопросы лежат в разных плоскостях. || Точка зрения на что-н., способ рассмотрения, обсуждения чего-н. (нов. книжн.). Изучить какой-н. вопрос в плоскости его экономического значения. 4. Плоское замечание (см. плоский в 3 знач.), плоская шутка. Говорить плоскости. ◊
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
пло́скость
1. свойство по значению прилагательного плоский; ровность, отсутствие впадин и выступов
2. геометр. поверхность, имеющая только два измерения, между любыми двумя точками которой можно провести прямую, которая целиком сольется с этой поверхностью
3. техн. крыло самолёта или другого летательного аппарата ◆ Расстилая по земле огненные шлейфы, рванулись с плоскостей наших самолётов реактивные снаряды. В. Л. Гуляев, «В воздухе «ИЛы»»
4. перен. область, сфера, круг явлений, отношений
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: замусоливать — это что-то нейтральное, положительное или отрицательное?