Что такое плоскость проекции

Лекция 1. Методы проецирования

1.1. Центральное проецирование

Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.

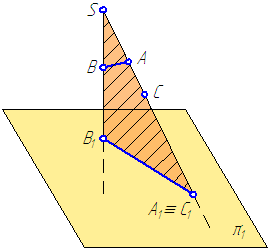
Центральное проецирование заключается в проведении через каждую точку (А, В, С,…) изображаемого объекта и определённым образом выбранный центр проецирования (S) прямой линии (SA, SB, >… — проецирующего луча).

Рисунок 1.1 – Центральное проецирование

Введём следующие обозначения (Рисунок 1.1):

SA, SB – проецирующие прямые (проецирующие лучи).

Примечание: левой клавишей мыши можно переместить точку в горизонтальной плоскости, при щелчке на точке левой клавишей мыши, изменится направление перемещения и можно будет ее переместить по вертикали.

Центральной проекцией точки называется точка пересечения проецирующей прямой, проходящей через центр проецирования и объект проецирования (точку), с плоскостью проекций.

Докажем это утверждение.

На рисунке 1.1: точка А₁ – центральная проекция точки А на плоскости проекций π₁. Но эту же проекцию могут иметь все точки, лежащие на проецирующей прямой. Возьмём на проецирующей прямой SA точку С. Центральная проекция точки С (С₁) на плоскости проекций π₁ совпадает с проекцией точки А (А₁):

Следует вывод, что по проекции точки нельзя судить однозначно о её положении в пространстве.

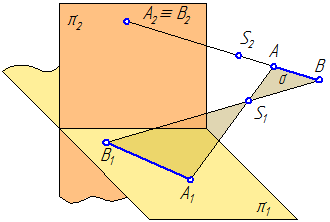
Чтобы устранить эту неопределенность, т.е. сделать чертеж обратимым, введём еще одну плоскость проекций (π₂) и ещё один центр проецирования (S₂) (Рисунок 1.2).

Рисунок 1.2 – Иллюстрация 1-го и 2-го свойств

Построим проекции точки А на плоскости проекций π₂. Из всех точек пространства только точка А имеет своими проекциями А₁ на плоскость π₁ и А₂ на π₂ одновременно. Все другие точки лежащие на проецирующих лучах будут иметь хотя бы одну отличную проекцию от проекций точки А (например, точка В).

Докажем данное свойство.

Соединим точки А и В между собой (Рисунок 1.2). Получим отрезок АВ, задающий прямую. Треугольник ΔSAB задает плоскость, обозначенную через σ. Известно, что две плоскости пересекаются по прямой: σ∩π₁=А₁В₁, где А₁В₁ – центральная проекция прямой, заданной отрезком АВ.

Метод центрального проецирования – это модель восприятия изображения глазом, применяется главным образом при выполнении перспективных изображений строительных объектов, интерьеров, а также в кинотехнике и оптике. Метод центрального проецирования не решает основной задачи, стоящей перед инженером – точно отразить форму, размеры предмета, соотношение размеров различных элементов.

1.2. Параллельное проецирование

Рассмотрим метод параллельного проецирования. Наложим три ограничения, которые позволят нам, пусть и в ущерб наглядности изображения, получить чертёж более удобным для использования его на практике:

Таким образом, наложив эти ограничения на метод центрального проецирования, мы пришли к его частному случаю – методу параллельного проецирования (Рисунок 1.3).Проецирование, при котором проецирующие лучи, проходящие через каждую точку объекта, параллельно выбранному направлению проецирования P, называется параллельным.

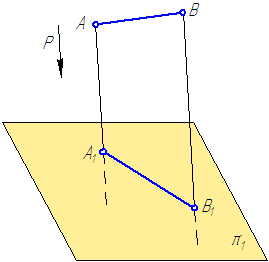
Рисунок 1.3 – Метод параллельного проецирования

Проведём через точки А и В проецирующие лучи, параллельные заданному направлению проецирования Р. Проецирующий луч проведённый через точку А пересечёт плоскость проекций π₁ в точке А₁. Аналогично проецирующий луч, проведённый через точку В пересечет плоскость проекций в точке В₁. Соединив точки А₁ и В₁, получим отрезок А₁ В₁– проекция отрезка АВ на плоскость π₁.

1.3. Ортогональное проецирование. Метод Монжа

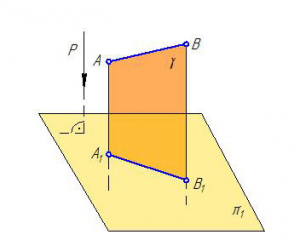
Четырехугольник АА₁В₁В задаёт плоскость γ, которая называется проецирующей, поскольку она перпендикулярна к плоскости π₁ (γ⊥π₁). В дальнейшем будем использовать только прямоугольное проецирование.

Рисунок 1.4 – Ортогональное проецирование

Рисунок 1.5- Монж, Гаспар (1746-1818)

Основоположником ортогонального проецирования считается французский учёный Гаспар Монж (Рисунок 1.5).

До Монжа строители, художники и учёные обладали довольно значительными сведениями о проекционных способах, и, всё же, только Гаспар Монж является творцом начертательной геометрии как науки.

Гаспар Монж родился 9 мая 1746 года в небольшом городке Боне (Бургундия) на востоке Франции в семье местного торговца. Он был старшим из пяти детей, которым отец, несмотря на низкое происхождение и относительную бедность семьи, постарался обеспечить самое лучшее образование из доступного в то время для выходцев из незнатного сословия. Его второй сын, Луи, стал профессором математики и астрономии, младший — Жан также профессором математики, гидрографии и навигации. Гаспар Монж получил первоначальное образование в городской школе ордена ораторианцев. Окончив её в 1762 году лучшим учеником, он поступил в колледж г. Лиона, также принадлежавший ораторианцам. Вскоре Гаспару доверяют там преподавание физики. Летом 1764 года Монж составил замечательный по точности план родного города Бона. Необходимые при этом способы и приборы для измерения углов и вычерчивания линий были изобретены самим составителем.

Во время обучения в Лионе получил предложение вступить в орден и остаться преподавателем колледжа, однако, вместо этого, проявив большие способности к математике, черчению и рисованию, сумел поступить в Мезьерскую школу военных инженеров, но (из-за происхождения) только на вспомогательное унтер-офицерское отделение и без денежного содержания. Тем не менее, успехи в точных науках и оригинальное решение одной из важных задач фортификации (о размещении укреплений в зависимости от расположения артиллерии противника) позволили ему в 1769 году стать ассистентом (помощником преподавателя) математики, а затем и физики, причём уже с приличным жалованием в 1800 ливров в год.

В 1770 году в возрасте 24-х лет Монж занимает должность профессора одновременно по двум кафедрам — математики и физики, и, кроме того, ведёт занятия по резанию камней. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке – начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года, книга вышла под названием Начертательная геометрия (Géométrie descriptive) (стенографическая запись этих лекций была сделана в 1795 году). Изложенный в ней подход к чтению лекций по этой науке и выполнению упражнений сохранился до наших дней. Еще один значительный труд Монжа – Приложение анализа к геометрии (L’application de l’analyse à la géometrie, 1795) – представляет собой учебник аналитической геометрии, в котором особый акцент делается на дифференциальных соотношениях.

В 1780 был избран членом Парижской академии наук, в 1794 стал директором Политехнической школы. В течение восьми месяцев занимал пост морского министра в правительстве Наполеона, заведовал пороховыми и пушечными заводами республики, сопровождал Наполеона в его экспедиции в Египет (1798–1801). Наполеон пожаловал ему титул графа, удостоил многих других отличий.

Метод изображения объектов по Монжу заключается в двух основных моментах:

1. Положение геометрического объекта в пространстве, в данном примере точки А, рассматривается относительно двух взаимно перпендикулярных плоскостей π₁ и π₂ (Рисунок 1.6).

Они условно разделяют пространство на четыре квадранта. Точка А расположена в первом квадранте. Декартова система координат послужила основой для проекций Монжа. Монж заменил понятие координатных осей проекций на линию пересечения плоскостей проекций (ось проекций) и предложил совместить координатные плоскости в одну путем поворота их вокруг координатных осей.

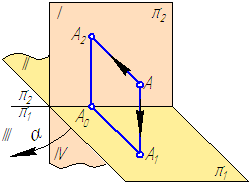
Рисунок 1.6 – Модель построения проекций точки

π₁ – горизонтальная (первая) плоскость проекций

π₂ – фронтальная (вторая) плоскость проекций

Рассмотрим пример проецирования точки А на две взаимно перпендикулярные плоскости проекций π₁ и π₂.

Опустим из точки А перпендикуляры (проецирующие лучи) на плоскости π₁ и π₂ и отметим их основания, то есть точки пересечения этих перпендикуляров (проецирующих лучей) с плоскостями проекций. А₁ – горизонтальная (первая) проекция точки А;А₂ – фронтальная (вторая) проекция точки А; АА₁ и АА₂ – проецирующие прямые. Стрелки показывают направление проецирования на плоскости проекций π₁ и π₂. Такая система позволяет однозначно определить положение точки относительно плоскостей проекций π₁ и π₂:

2. Совместим поворотом вокруг оси проекций π₂/π₁ плоскости проекций в одну плоскость (π₁ с π₂), но так, чтобы изображения не накладывались друг на друга, (в направлении α, Рисунок 1.6), получим изображение, называемое прямоугольным (ортогональным) чертежом (Рисунок 1.7):

Рисунок 1.7 – Ортогональный чертеж

1.4. Прямоугольные проекции точки. Свойства ортогонального чертежа

1. Две прямоугольные проекции точки лежат на одной линии проекционной связи, перпендикулярной к оси проекций.

2. Две прямоугольные проекции точки однозначно определяют её положение в пространстве относительно плоскостей проекций.

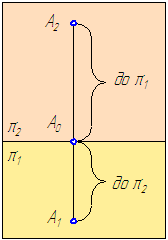
Убедимся в справедливости последнего утверждения, для чего повернём плоскость π₁ в исходное положение (когда π₁⊥π₂). Для того, чтобы построить точку А необходимо из точек А₁ и А₂ восстановить проецирующие лучи, а фактически – перпендикуляры к плоскостям π₁и π₂, соответственно. Точка пересечения этих перпендикуляров фиксирует в пространстве искомую точку А. Рассмотрим ортогональный чертеж точки А (Рисунок 1.8).

Рисунок 1.8 – Построение эпюра точки

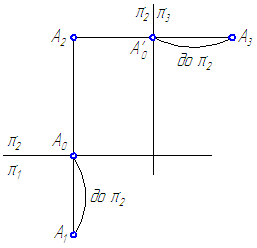
Введём третью (профильную) плоскость проекций π₃ перпендикулярную π₁ и π₂ (задана осью проекций π₂/π₃).

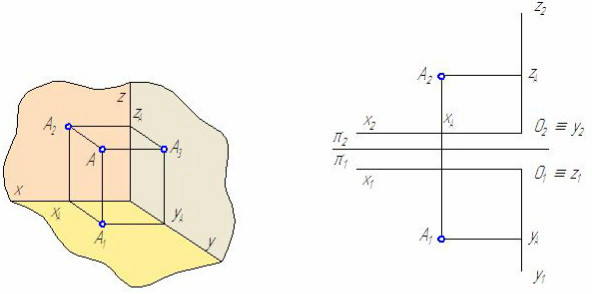
Расстояние от профильной проекции точки до вертикальной оси проекций А‘₀A₃ позволяет определить расстояние от точки А до фронтальной плоскости проекций π₂. Известно, что положение точки в пространстве можно зафиксировать относительно декартовой системы координат с помощью трёх чисел (координат) A(X_A; Y_A; Z_A) или относительно плоскостей проекций с помощью её двух ортогональных проекций (A₁=(X_A; Y_A); A₂=(X_A; Z_A)). На ортогональном чертеже по двум проекциям точки можно определить три её координаты и, наоборот, по трём координатам точки, построить её проекции (Рисунок 1.9, а и б).

а б
Рисунок 1.9 – Построение эпюра точки по её координатам

По расположению на эпюре проекций точки можно судить о её расположении в пространстве:

Для определения в каком квадранте пространства расположена точка, достаточно определить знак координат точки.

Зависимости квадранта положения точки и знаков координат

X	Y	Z
I	+	+	+
II	+	—	+
III	+	—	—
IV	+	+	—

Упражнение

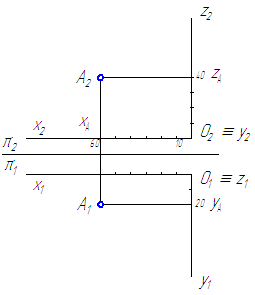
Решение задачи: по оси OX отложить значение координаты X_A=60, затем через эту точку на оси OX восстановить линию проекционной связи, перпендикулярную к OX, по которой вверх отложить значение координаты Z_A=40, а вниз – значение координаты Y_A=20 (Рисунок 1.10). Все координаты положительные, значит точка расположена в I квадранте.

Рисунок 1.10 – Решение задачи

1.5. Задачи для самостоятельного решения

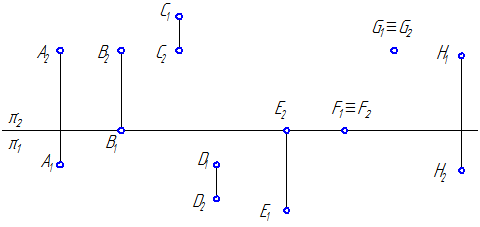
1. По эпюру определите положение точки относительно плоскостей проекций (Рисунок 1.11).

Рисунок 1.11

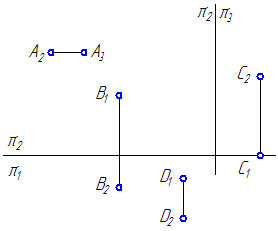
2. Достройте недостающие ортогональные проекции точек А, В, С на плоскости проекций π₁, π₂, π₃ (Рисунок 1.12).

Рисунок 1.12

3. Постройте проекции точки:

4. Постройте ортогональные проекции точки К, расположенной во втором квадранте и удаленной от плоскостей проекций π₁ на 40 мм, от π₂ — на 15 мм.

Источник

Лекция 3. Плоскость

3.1. Способы задания плоскости на ортогональных чертежах

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂ и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

Рисунок 3.6 – Принадлежность прямой плоскости

\left.\begin\alpha=m\parallel n,\\D\in\alpha\\C\in\alpha\\\end\right\> \Longrightarrow CD\in\alpha

Упражнение

Рисунок 3.7 – Решение задачи

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

\alpha=m\cap n\\\left.\begina_2\parallel m_2\\a_1\parallel m_1\\\end\right\> \Rightarrow a\parallel\alpha

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π₂ (рис. 3.15)
Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.
Направление взгляда на π₂ показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.
4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π₁.
Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.
Направление взгляда на π₁ показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.
2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Упражнение

Алгоритм решения задачи :

\left.\beginAB\cap\sigma=K\\AC\cap\sigma=L\\\end\right\> \left.\begin\Rightarrow A_1B_1\cap\sigma_1=K_1 \rightarrow K_2\\\Rightarrow A_1C_1\cap \sigma_1=L_1 \rightarrow L_2\\\end\right.

KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

\left.\begin\alpha\cap\sigma=(4-5)\\\beta\cap\sigma=(3-2)\\\end\right\>\\\left.\begin\alpha\cap\tau=(6-7)\\\beta\cap\tau=(1-8)\\\end\right\>\left.\begin(4_1-5_1)\cap(3_1-2_1)=M_1\rightarrow M_2\\(6_1-7_1)\cap(1_1-8_1)=N_1\rightarrow N_2\\\end\right\>\rightarrow\\\left.\beginM_1N_1\\M_2N_2\\\end\right\>\Rightarrow\alpha\cap\beta=MN

Упражнение

Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π₂, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π₂ (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π₂ и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C₁D₁ должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.

Источник