Что такое плоскость прямая луч
Плоскость. Прямая. Луч.
Размеры тетради не позволяют строить отрезки большой длины. А вообразите себе, что тетрадный лист вырос до размеров стола, теннисного корта, даже футбольного поля. Такой лист является примером, или как еще принято говорить, моделью части плоскости.
Плоскость бесконечна, поэтому ее нельзя отобразить. Эту геометрическую фигуру можно вообразить.
Теперь понятно, что на плоскости можно начертить отрезок очень большой длины. Более того, любой отрезок с помощь линейки можно продлить в обе стороны. Мысленно это можно сделать неограниченно, и тогда мы получим фигуру, которую называют прямой.
Прямая не имеет концов. Она бесконечна. Поэтому на рисунке мы изображаем только часть прямой − отрезок.
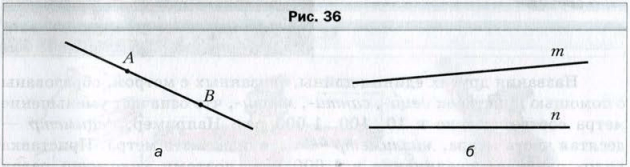
Отметим на листе бумаги две точки A и B. Проведем через них прямую (рис. 36 a). Если попытаемся провести через эти точки еще одну прямую, то нам это не удастся.
Через две точки проходит только одна прямая.
Это свойство позволяет обозначать прямую, называя две любые ее точки. Так, прямую, изображенную на рисунке 36, a, обозначают одним из двух способов : AB или BA. Читают: «прямая AB» или «прямая BA».
Иногда прямые обозначают одной строчной латинской буквой. На рисунке 36, б изображены прямые m и n.
Проведем прямую AB и отметим на ней точку O ( рис. 37, а). Эта точка делит прямую на две части. Каждую из этих частей называют лучом с началом в точке O. Конца у луча нет.
Так же, как и прямую, луч обозначают двумя прописными буквами. Сначала записывают букву, обозначающую начало луча, а потом букву, обозначающую какую−либо другую точку этого луча. Например, луч с началом в точке O ( рис. 37, б) можно обозначить OA или OB.
Луч − это еще один пример геометрической фигуры.
Плоскость. Прямая. Луч
Содержание
Плоскость
Посмотрев вокруг, ты увидишь множество плоских вещей. Поверхность стола, лист бумаги, оконное стекло… А представьте себе, как будто эти поверхности не имеют конца и края, как будто они простираются за пределы Земли!
У математической плоскости нет границ. Она простирается бесконечно в любом направлении.
Прямая
Начертим отрезок АВ (рисунок 1). Он ограничен двумя точками. Теперь проведём по линейке линии таким образом, чтобы он продолжался в обе стороны (рисунок 2). У нас получилась прямая, на которой лежат точки А и В.
Конечно, мы можем приложить линейку и измерить ту линию на рисунке 2. Даже если мы будем чертить прямую не в тетрадке, а, скажем, на полу, и продолжать её в обе стороны до самых стен, её всё равно можно измерить. Но говоря о математической прямой, мы подразумеваем, что она не заканчивается и продолжается до бесконечности.
Прямая бесконечна. Она неограниченно продолжается в обе стороны.
Через любые две точки проходит только одна прямая.
Прямая обозначается двумя буквами, по тем точкам, через которые она проходит. На рисунке 2 – прямая АВ (можно также назвать ВА).
Теперь нарисуем две пересекающиеся прямые, АВ и СD. Та точка, в которой они пересекаются, общая для обеих прямых. Она делит каждую прямую на две части.
Луч
Начертим прямую и поставим на ней точку. Эта точка разделяет прямую на две части, каждую из них называют лучом.
У прямой нет ни начала, ни конца.
У луча тоже нет конца, но есть начало.
Представьте, что у вас в руке фонарик, и из него бьёт луч света. Фонарик и будет началом луча.
Для обозначения луча называют его начало и какую-нибудь из точек, лежащих на этом луче. Но переставлять буквы в названии уже нельзя, первой всегда будет идти буква, обозначающая точку-начало.
Например, луч на рисунке 6 называется ОА.
Лучи, на которые точка разбивает прямую, называются дополнительными друг другу.
Это как бы две половинки одной прямой.
Луч продолжается до бесконечности, и на нём можно поставить бесконечное число точек. Но всё равно будут точки, которые остаются вне этого луча. Представьте, что вы светите фонариком перед собой. То, что находится справа, слева, сзади, сверху – всё остаётся вне луча света.
На рисунке 7 показано, что точки В, С, D лежат на луче, а E и F – нет.
Урок 4 Бесплатно Плоскость. Прямая. Луч
В этом уроке мы продолжим разговор про геометрию, начатый в прошлых уроках.
Мы рассмотрим такие понятия, как плоскость, прямая, луч, поговорим еще раз про отрезки. Также обсудим, как все эти объекты могут располагаться друг относительно друга. Начнем же.
Плоскость
Важно отметить, что в начале разбора приходится некоторые понятия принимать как нечто, что не требует определения, к таким понятиям относятся понятия прямой и точки.
Немецкий учений Гильберт как-то сказал на эту тему, что “точкой можно назвать хоть стул”, тем самым говоря, что вся наша модель строится на некоторых условностях.
С этим пониманием приступим к первой теме урока.
Для начала нам нужно понять, что такое поверхность.
Есть много строгих математических формулировок, но они уместны скорее в высших учебных заведениях, пока будет достаточно обиходного понятия поверхности.
Будем понимать под поверхностью непрерывное множество точек, границу, отделяющую геометрическое тело от внешнего пространства.
Представьте себе поверхность рабочего стола, футбольного мяча или любого другого предмета.
Также известно, что некоторые поверхности, например, рабочего стола, плоские.
Плоская в данном случае обозначает, что если через любые две точки, принадлежащие этой плоскости, провести прямую, то она будет лежать в этой плоскости.
В самом деле, если нарисовать две точки на поверхности стола и соединить их прямой, то эта прямая будет лежать в плоскости стола.
Если же отметить две точки на шаре, то (тут нужен некоторый мысленный эксперимент) прямая, соединяющая их, будет проходить внутри шара, а не по его поверхности. Таким образом, поверхность шара не плоская, не является плоскостью.
Обычно на рисунках плоскость обозначается конечной, в крайнем случае лист бумаги или экран компьютера конечен.
Но это лишь обозначения, сама плоскость бесконечна.
Поверхности и плоскости принято обозначать двумя способами: с помощью трех латинских букв, соответствующих трем точкам плоскости, или одной греческой.
Выше изображена четырехугольная пирамида. В ней можно насчитать 5 плоскостей:
Согласись, две точки слишком мало, чтобы обозначить плоскость: на данном рисунке, например, есть две плоскости, проходящие через точки A и E, а четыре точки уже несут избыточную информацию, поэтому плоскости обозначают тремя точками.
Иногда плоскость обозначают одной строчной греческой буквой, например, так:
Точка может принадлежать плоскости (лежать в ней) или не принадлежать плоскости.
Пройти тест и получить оценку можно после входа или регистрации
Прямая
Проведем отрезок, назовем его AB.
А теперь продолжим его по линейке за концы в обе стороны:
Так мы получим прямую. Прямая, как и плоскость, бесконечна.
Если плоскость простирается во все стороны, то прямая в конкретные два направления.
Как и в случае с плоскостью, невозможно изобразить нечто бесконечное в тетрадях или на мониторах, так как эти объекты имеют границы, поэтому любое изображение будет лишь обозначать прямую.
Для обозначения прямой используются две заглавные латинские буквы, так выше приведенную прямую можно назвать “прямая АВ” или “прямая ВА”.
Также иногда прямые обозначают строчными латинскими буквами:
Вот, например, прямая а.
Через любые две точки проходит единственная прямая.
То есть ситуация, при которой между двумя точками нет ни одной прямой или, напротив, более одной, невозможна.
Так на рисунке выше точки А и В принадлежат прямой АВ.
Рассмотрим другой рисунок:
В данном случае точки С и D не принадлежат прямой АВ.
Мы можем представить себе прямую, нарисованную на плоском листе бумаги.
Так и в математике прямые могут принадлежать плоскостям.
Можно изобразить это так:
На рисунке прямая а, принадлежит плоскости \(\mathbf<\alpha>\)
Обычно такие рисунки сопровождают текстовым описанием для того, чтобы их понимали однозначно.
Также мы можем видеть прямые и на других рисунках.
Мы знаем, что через любые две точки проходит прямая.
Так что смотря на рисунок выше мы можем говорить про прямые AE, ED, DC, AC, AB, EB, DB, CB
Точно также можно видеть прямые не только на объемных рисунках, но и на плоских.
Так на этом рисунке можно говорить про прямые AB, BC и AC
Также отношение “принадлежит” обладает в данном случае таким свойством: если точка принадлежит прямой, а прямая принадлежит плоскости, то верно, что эта точка принадлежит плоскости.
Посмотрим на рисунок:
Если нам известно, что точка А принадлежит прямой а и прямая а принадлежит плоскости \(\mathbf<\alpha>\), то очевидно, что и сама точка А принадлежит прямой \(\mathbf<\alpha>\)
Про прямые надо знать такое определение:
Если две прямые имеют общую точку, то говорят, что они пересекаются в этой точке.
В данном случае это точка О.
Пройти тест и получить оценку можно после входа или регистрации
Любая точка на прямой делит ее на две части.
Каждую из этих частей называют лучом.
Сама такая точка будет называться началом луча.
Точка М является началом обоих лучей.
Лучи МА и МВ называются дополнительными друг другу. Это такие лучи, на которые точка разбивает прямую.
Давая лучам название, первой буквой пишут вершину луча, вторая определяет направление.
Это может быть как точка на соответствующей прямой, так и просто буква, подписанная возле соответствующей части прямой, как на рисунке выше.
Как и в случае с прямой, точки могут лежать и не лежать на луче.
Посмотрим, как лежат точки относительно луча MB.
Точки Р и К не лежат на прямой АВ, значит и на луче, как на части прямой, лежат не могут.
Точка С не лежит на луче МВ, так как находится с другой стороны от точки М, луч уходит в сторону В.
Научимся видеть лучи еще в некоторых ситуациях.
Например, сколько лучей образуются при пересечении прямых?
Обозначим прямые как АВ и CD, точку пересечения назовем точкой О.
Имеем одну точку, которая может стать началом луча, от нее отходят четыре половины прямых.
А полупрямая это и есть луч. Значит, при пересечении двух прямых от точки их пересечения будет отходить 4 луча.
Посмотрим еще раз на картинку с треугольником АВС.
В случае с лучом принципиально, где у него начало, а где продолжение (конца не бывает).
Тогда у нас есть 3 точки-кандидата на начало луча. От каждой точки отходит по два отрезка, но чтобы обозначить луч нам нужна любая точка с продолжения, так что получается, что от каждой вершины отходят по 2 луча и всего на рисунке можно увидеть 6 лучей, если не ставить дополнительных точек.
Пройти тест и получить оценку можно после входа или регистрации
Дополнительная информация
Геометрия, про которую мы сегодня говорили, называется Евклидовой.
Как уже было сказано, часть понятий является фундаментальными. В данном случае первоначальные понятия Евклидовой геометрии предложил, как следует из названия, Евклид, живший в Древней Греции.
Если быть более точным, жил он в Александрии и являлся первым математиком Александрийской школы.
О самом Евклиде, к сожалению, известно крайне мало информации.
Самая его известная книга “Начала” содержала в себе факты о геометрии, а также об арифметике.
Иногда книга издавалась с комментариями. Из одного из таких изданий с комментариями от Прокла мы знаем что-то про Евклида, хотя Прокл жил примерно на 800 лет позже Евклида.
Также существуют скульптуры и портреты, посвященные Евклиду, но есть сомнения в их достоверности.
По сути единственное, что известно более-менее точно, так это то, что ученые занимались вопросами геометрии еще в те времена.
Сохранились и другие работы Евклида, например, ему приписывают “Деление канона” (трактат о теории музыки), но им уделяется меньше внимания.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Опорный конспект по теме Плоскость. Прямая. Луч.
Справочник 3 Плоскость. Прямая. Луч.
Плоскость — понятие, не имеющее значения. Представление о плоскости дают: поверхность стола, оконного стекла, поверхность озера в тихую погоду и т.п. Плоскость – это воображаемая абсолютно ровная и неизменяемая поверхность, которая не имеет толщины, но обладает бесконечными длиной и шириной. Плоскость нельзя измерять, потому что она бесконечная. Плоскость нельзя согнуть, в каком бы положении она ни находилась.
Если две прямые пересекаются в какой-либо точке, то эта точка является точкой пересечения прямых. Точка пересечения прямых является точкой, принадлежащей каждой из прямых. В нашем примере прямые а и в пересекаются в точке О. Точка О делит каждую прямую на две части.
Через две любые точки на плоскости можно провести единственную прямую.
Луч (полупрямая) — часть прямой, состоящая из всех точек этой прямой, которая лежит по одну сторону от данной на ней точки (начало луча). Луч – это часть прямой, которая начинается в определенной точке и длится бесконечно в одну сторону. У луча есть начало, но нет конца. От прямой луч отличается тем, что луч бесконечно продолжается только в одну сторону.
Лучи обозначаются a – строчной (маленькая) буква латинского алфавита; OF – точками, расположенными на луче. При этом на первом месте всегда пишут точку начала луча, а на втором – любую точку, которая принадлежит лучу. Переставлять буквы в названии луча нельзя.
CB и CH – дополнительные друг другу лучи, BC и BH – совпадающие лучи, HC и HB – совпадающие лучи.
При пересечении двух прямых образовалось 4 луча, с общим началом О.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Математика. 5 класс
Конспект урока
Прямая, луч, отрезок
Перечень рассматриваемых вопросов:
— понятия «прямая», «луч», «отрезок»;
— отличия прямой, луча, отрезка;
— прямая, луч, отрезок на чертежах, рисунках и моделях.
Отрезок – часть прямой, ограниченный двумя точками.
Концы отрезка – точки, ограничивающие отрезок.
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф.Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009.–142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы.// И. Ф. Шарыгин, А. В. Шевкин.– М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Основными геометрическими фигурами принято считать плоскость, прямую и точку, все остальные фигуры образуются из них или их частей, поясним сказанное на примерах. Начнём с того, что различные геометрические фигуры располагаются на плоскости. Представление о плоскости даёт нам, например, поверхность стола или школьной доски. Стоит отметить, что эти поверхности имеют края. У плоскости нет краёв. Она безгранично простирается во всех направлениях.
Введём ещё одно понятие – прямая. Её обозначают малой латинской буквой (например, а) или двумя заглавными буквами (например, АВ, если на прямой отмечены соответствующие точки).
Стоит заметить, что прямая линия не имеет ни начала, ни конца, поэтому её изображение можно продолжить в обе стороны. Две различные прямые могут иметь только одну общую точку, в этом случае говорят, что прямые пересекаются.
Две различные прямые на плоскости могут и не пересекаться, сколько бы их не продолжали, такие прямые называют параллельными.
Параллельные прямые можно легко построить с помощью линейки и угольника, передвигая его вдоль линейки так, как показано на рисунке.
Через любые две точки можно провести только одну прямую.
Выполним построение. Для этого отметим две точки А и В и проведём через эти точки прямую b.
Провести через точки А и В другую прямую, отличную от прямой b, нельзя.
Используя прямую и точку в виде деталей геометрического конструктора, можно создавать новые геометрические объекты.
Например, начертим прямую с и отметим на ней точку А. Точка А разделила прямую на две части.
Каждую из этих частей называют лучом, исходящим из точки А.
Итак, луч – это прямая линия, которая имеет начало, но не имеет конца.
Луч следует обозначать двумя заглавными буквами латинского алфавита, при этом на первое место надо ставить обозначение начала луча. Например, АВ, как в нашем случае, где точка А – начало луча.
Переставлять буквы в названии луча нельзя.
Теперь рассмотрим ещё одно важное геометрическое понятие – отрезок.
Отрезком называют часть прямой между двумя точками. Отрезок обозначают АВ или ВА. При этом точки А и В называют концами отрезка АВ.
В отличие от луча, в названии отрезка переставлять буквы допустимо, поэтому его можно обозначить как АВ, так и ВА.
Заметим, что два отрезка называются равными, если они совмещаются при наложении.
Итак, сегодня мы познакомились с понятиями прямая, луч, отрезок, как одними из основополагающих понятий в геометрии.
Помимо геометрии, мы можем встретить слово «луч» и в других научных областях.
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: добавление подписей к изображениям.
Разместите нужные подписи к изображениям.
Для выполнения задания обратитесь к теоретическому материалу урока.
№ 2. Тип задания: подстановка элементов в пропуски в тексте.
Вставьте в текст нужные слова.
Через__________ две____________ можно провести только одну _________.
Слова: любые; точки; прямую; ломаную.
Правильный ответ: через любые две точки можно провести только одну прямую.