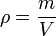Что такое плотность 7 класс физика определение

Плотность (физика)

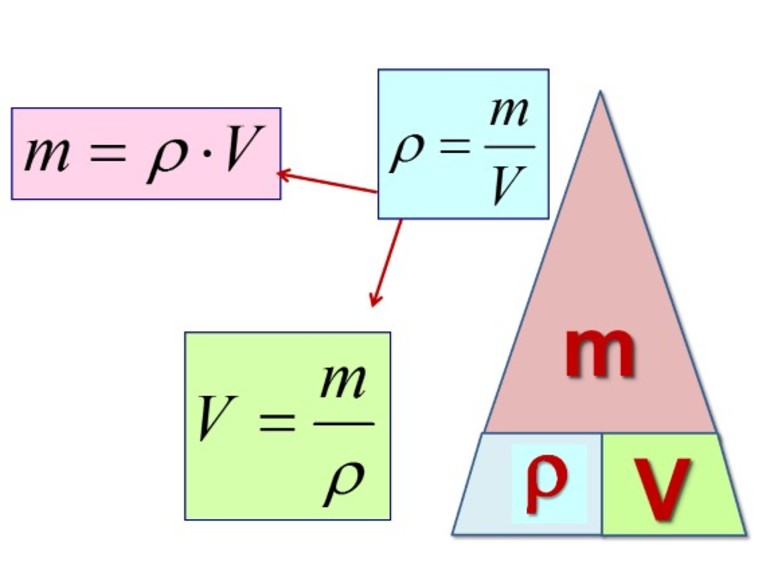
Плотность — физическая величина равная отношению массы тела к его объему, показывает массу единичного объема вещества.

Содержание

Виды плотности и единицы измерения

Плотность измеряется в кг/м³ в системе СИ и в г/см³ в системе СГС.

Для сыпучих и пористых тел различают

Формула нахождения плотности

Плотность находится по формуле:

Зависимость плотности от температуры

Как правило, при уменьшении температуры плотность увеличивается, но есть вещества, чья плотность ведет себя иначе, например, вода, бронза и чугун.

При фазовых переходах, изменении агрегатного состояния плотность вещества меняется скачкообразно.

Самую большую плотность во Вселенной имеют черные дыры (ρ

10 11 кг/м³). Самую низкую плотность имеет межгалактическая среда (ρ

В астрономии большое значение имеет средняя плотность небесных тел, по ней можно приблизительно определить состав этого тела.

Плотности некоторых газов

Плотность газов и паров (0° С, 101325 Па), кг/м³

Азот	1,250	Кислород	1,429
Аммиак	0,771	Криптон	3,743
Аргон	1,784	Ксенон	5,851
Водород	0,090	Метан	0,717
Водяной пар (100° С)	0,598	Неон	0,900
Воздух	1,293	Углекислый газ	1,977
Хлор	3,214	Гелий	0,178
Этилен	1,260

Измерение плотности

Ссылки

Полезное

Смотреть что такое «Плотность (физика)» в других словарях:

ФИЗИКА. — ФИЗИКА. 1. Предмет и структура физики Ф. наука, изучающая простейшие и вместе с тем наиб. общие свойства и законы движения окружающих нас объектов материального мира. Вследствие этой общности не существует явлений природы, не имеющих физ. свойств … Физическая энциклопедия

Физика звёзд — Физика звезд одна из отраслей астрофизики, изучающая физическую сторону звезд (масса, плотность, …). Содержание 1 Размеры, массы, плотность, светимость звезд 1.1 Масса звёзд … Википедия

Плотность состояний — величина, определяющая количество энергетических уровней в интервале энергий на единицу объёма в трёхмерном случае (на единицу площади в двумерном случае). Является важным параметром в статистической физике и физике твёрдого тела. Термин может… … Википедия

ФИЗИКА — наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, св ва и строение материи и законы её движения. Понятия Ф. и её законы лежат в основе всего естествознания. Ф. относится к точным наукам и изучает количеств … Физическая энциклопедия

ФИЗИКА — ФИЗИКА, наука, изучающая совместно с химией общие законы превращения энергии и материи. В основе обеих наук лежат два основных закона естествознания закон сохранения массы (закон Ломоносова, Лавуазье) и закон сохранения энергии (Р. Майер, Джауль… … Большая медицинская энциклопедия

Физика взрыва — (a. explosion physics; н. Physik der Explosion; ф. physique de l explosion; и. fisica de explosion, fisica de estallido, fisica de detonacion) наука, изучающая явление взрыва и механизм его действия в среде. Hарушение механич.… … Геологическая энциклопедия

Физика моря — физика океана, раздел геофизики (См. Геофизика), посвященный изучению физических процессов в Мировом океане. Термин «физическая океанография» иногда используется как синоним Ф. м., но в узком смысле означает часть Ф. м., посвященной… … Большая советская энциклопедия

Физика — I. Предмет и структура физики Ф. – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы её движения. Поэтому понятия Ф. и сё законы лежат в основе всего… … Большая советская энциклопедия

Физика — 1) Ф. и ее задачи. 2) Методы Ф. 3) Гипотезы и теории. 4) Роль механики и математики в Ф. 5) Основные гипотезы Ф.; вещество и его строение. 6) Кинетическая теория вещества. 7) Действие на расстоянии. 8) Эфир. 9) Энергия. 10) Механические картины,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Плотность — У этого термина существуют и другие значения, см. Плотность (значения). Плотность Размерность L−3M Единицы измерения СИ … Википедия

Источник

Плотность вещества

Содержание

Любое физическое тело имеет некоторую массу. Определить массу тела можно с помощью весов — путем взвешивания. А также и более сложным способом — при взаимодействии двух тел, зная их скорости, и массу одного из них. Согласитесь, что первый способ — более легкий и практичный.

Тела имеют разные характеристики: разные размеры и формы, разные материалы, разные состояния и структуру (жидкие, твердые и газообразные), разные массы.

Сегодня мы познакомимся с такой характеристикой как плотность, она покажет и объяснит нам, как может различаться масса тел одинаковой формы и размера.

Опытное подтверждение

Рассмотрим опыт, представленный на рисунке 1.

Рисунок 1. Взвешивание двух одинаковых тел, состоящих из разных веществ.

Возьмем два одинаковых цилиндра: они одинаковой формы и объема, но изготовлены из разных материалов.

Один сделан из алюминия, а другой из свинца. Поместим их на разные чаши весов.

В итоге, мы увидим, что масса цилиндра из алюминия будет почти в 4 раза меньше массы цилиндра из свинца.

Тела, имеющие равные объемы, но состоящие из разных веществ, имеют разные массы.

На рисунке изображены 3 тела массой 100 г: лед, железо и золото.

Рисунок 2. Тела одинаковой массы, но состоящие из разных веществ.

Здесь представлены тела одинаковой массы, но взгляните на их объем. Объем льда будет почти в 8,5 раз больше объема куска железа той же массы. А объем золота будет почти в 3 раза меньше объема железа.

Тела с равными массами, но состоящие из разных веществ, имеют разные объемы.

Определение плотности вещества

Вышерассмотренные свойства веществ, из которых состоят тела, объясняется тем, что разные вещества имеют разную плотность.

На рисунке 3 приведены другие примеры тел равного объема, но состоящих из разных веществ.

Рисунок 3. Тела равного объема, состоящие из разных веществ.

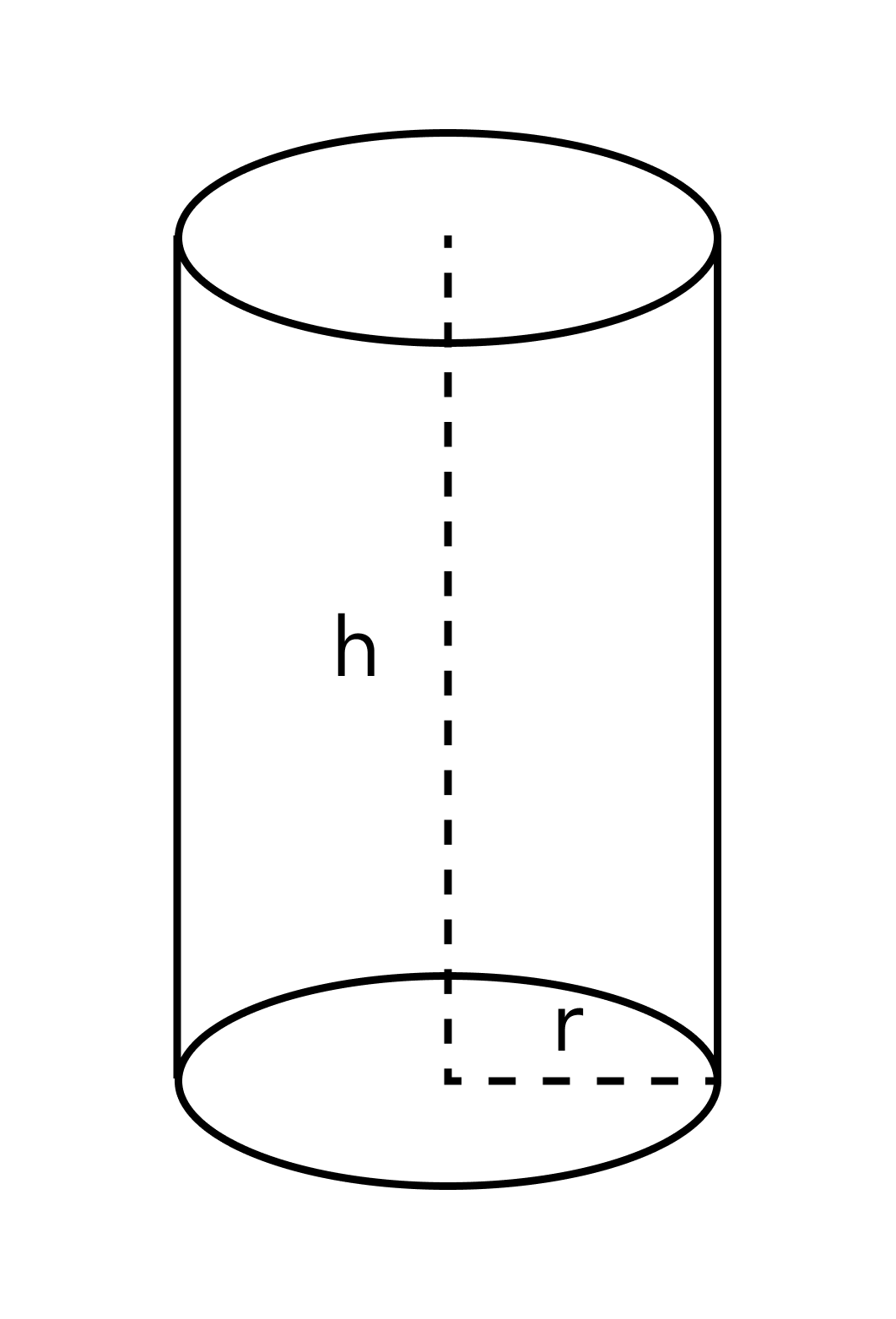
Плотность — это физическая величина, которая равна отношению массы тела к его объему:

$$плотность = \frac<масса><объем>$$

$$\rho = \frac$$

Единицы измерения плотности

В СИ плотность вещества измеряется в килограммах на кубический метр ($1 \frac<кг><м^3>$).

Также часто используется другая единица измерения — граммы на кубический сантиметр ($1 \frac<г><см^3>$) (рисунок 4).

Таблицы плотности некоторых тел и веществ

Плотность одного и того же вещества в твердом, жидком и газообразном состояниях различна.

Рисунок 5. Плотности одного вещества в разных агрегатных состояниях.

Плотности различных твердых тел

Твердое тело	$\rho, \frac<кг><м^3>$	$\rho, \frac<г><см^3>$	Твердое тело	$\rho, \frac<кг><м^3>$	$\rho, \frac<г><см^3>$
Осмий	22 600	22,6	Мрамор	2700	2,7
Иридий	22 400	22,4	Стекло	2500	2,5
Платина	21 500	21,5	Фарфор	2300	2,3
Золото	19 300	19,3	Бетон	2300	2,3
Свинец	11 300	11,3	Кирпич	1800	1,8
Серебро	10 500	10,5	Сахар	1600	1,6
Медь	8900	8,9	Оргстекло	1200	1,2
Латунь	8500	8,5	Капрон	1100	1,1
Сталь, железо	7800	7,8	Полиэтилен	920	0,92
Олово	7300	7,3	Парафин	900	0,90
Цинк	7100	7,1	Лед	900	0,90
Чугун	7000	7,0	Дуб сухой	700	0,70
Корунд	4000	4,0	Сосна сухая	400	0,40
Алюминий	2700	2,7	Пробка	240	0,24

Таблица 1

Плотности различных жидкостей

Плотности различных газов

Примеры расчета плотности вещества

2. Канистра объемом 30 л наполнена бензином. Масса полной канистры составляет 21,3 кг. Рассчитайте плотность бензина.

Переведем литры в кубические метры ($1 л = 0,001 м^3$):

$30 \cdot 0,001 = 0,03 м^3$.

Дано:
$V = 30 л$
$m = 21,3 кг$

Показать решение и ответ

Решение:

Если мы сравним полученное значение с табличным, то получим подтверждение, что задача решена верно.

3. Деревянный брусок из березы имеет следующие размеры: длину 3 м, высоту 10 см, и ширину 50 см. Масса бруска составляет 75 кг. Найдите плотность березы.

Дано:
$а = 3 м$
$b = 10 см$
$c = 50 см$
$m = 75 кг$

Показать решение и ответ

Решение:
Найдем объем бруска:
$V = a \cdot b \cdot c = 3 м \cdot 0,1 м \cdot 0,5 м = 0,15 м^3$.

Источник

Плотность вещества – формула, единицы измерения, состав, что показывает (7 класс)

Как известно из курса физики 7 класса, одной из важнейших характеристик любого тела является его масса. Большие тела, как правило, тяжелы, мелкие — легки. Однако, если тела имеют одинаковые размеры, они вовсе не обязательно будут иметь одну и ту же массу. И это обязательно отразится на физических явлениях с этими телами. Как в физике учитывается различная масса одинаковых по размеру тел?

Масса и плотность вещества

Шарик для настольного тенниса весит 2,7 г.

Но такой же по размеру шарик из дерева будет весить 15–20 г, а из железа — 260 г. Если же шарик изготовить из свинца, его масса достигнет 380 г.

Столь большая разница в массе одинаковых по размеру тел объясняется тем, что элементарные частицы внутри различных веществ имеют различное пространственное расположение, и в одном и том же объёме помещается разное их количество. Например, в ядрах атомов свинца в среднем 208 нуклонов, составляющих основную массу. А в ядрах железа — только 56 нуклонов. В ядрах элементов, из которых состоят молекулы дерева и воздуха, нуклонов ещё меньше.

Мало того, в составе молекул и кристаллических решёток атомы могут находиться на разных расстояниях, и в одном и том же объёме будет помещаться их различное количество. Наконец, в газах молекулы находятся друг от друга на относительно больших расстояниях, это и объясняет лёгкость газов (и малую массу шарика от пинг-понга, на 99 % заполненного воздухом).

Возникает вопрос: как учесть эту разницу?

В физике для этого используется специальная величина — плотность, которая показывает, насколько сильно «упаковано» вещество в данном объёме.

В приведённом примере наивысшая плотность будет у свинцового шарика, наименьшая — у шарика для пинг-понга.

Формула плотности вещества

Из данной формулы можно получить единицу плотности. Поскольку масса измеряется в килограммах, а объём — в кубических метрах, то единицей измерения плотности будет килограмм на кубический метр:

Физический смысл плотности — это масса одного кубического метра данного вещества.

Рис. 1. Плотность вещества

Использование плотности в расчётах

Плотность вещества — это табличная величина, и она позволяет по известной массе вычислить объём тела, или наоборот, получить массу тела известного объёма.

Рис. 2. Таблица плотности разных веществ.

Например, в приведённом примере с шариками из различных веществ не требуется изготавливать шарики, чтобы знать их массу. Достаточно измерить диаметр шарика (для настольного тенниса он составляет 0,04 м) и по геометрическим формулам вычислить его объём (он составит 0,0000335 куб. м). Умножая полученный объём на плотность вещества, взятую из таблицы, можно получить вес шарика, не изготавливая и не взвешивая его. Например, стеклянный шарик такого размера будет весить около 85 г, а золотой шарик — 647 г.

Рис. 3. Взвешивание воздуха.

Что мы узнали?

Плотность — это физическая величина, показывающая, насколько сильно «упаковано» вещество в данном объёме. Она равна отношению массы вещества к объёму, занимаемому этой массой, и измеряется в килограммах на кубический метр.

Источник

Плотность вещества

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Масса

Начнем с самого сложного — с массы. Казалось бы, это понятие мы слышим с самого детства, примерно знаем, сколько в нас килограмм, и ничего сложного здесь быть не может. На самом деле, все сложнее.

В Международном бюро мер и весов в Париже есть цилиндр массой один килограмм. Материал этого цилиндра — сплав иридия и платины. Его масса равна одному килограмму, и этот цилиндр — эталон для всего мира.

Высота этого цилиндра приблизительно равна 4 см, но чтобы его поднять, нужно приложить немалую силу. Необходимость эту силу прикладывать обуславливается инерцией тел и математически записывается через второй закон Ньютона.

Второй закон Ньютона

F = ma

В этом законе массу можно считать неким коэффициентом, который связывает ускорение и силу. Также масса важна при расчете силы тяготения. Она является мерой гравитации: именно благодаря ей тела притягиваются друг к другу.

Закон Всемирного тяготения

F = GMm/R2

M — масса первого тела (часто планеты) [кг]

m — масса второго тела [кг]

R — расстояние между телами [м]

G — гравитационная постоянная

G = 6.67 × 10-11 м3 кг-1 с-2

Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз. Когда думаешь об этом, хочется взвешиваться исключительно на Луне🙃

Откуда берется масса

Физики убеждены, что у элементарных частиц должна быть масса. Доказано, что у электрона, например, масса есть. В противном случае они не могли бы образовать атомы и всю видимую материю.

Вселенная без массы представляла бы собой хаос из различных излучений, двигающихся со скоростью света. Не существовало бы ни галактик, ни звезд, ни планет. Здорово, что это не так, и у элементарных частиц есть масса. Только вот пока непонятно, откуда эта масса у них берется.

Мужчину на этой фотографии зовут Питер Хиггс. Ему мы обязаны за предположение, экспериментально доказанное в 2012 году, что массу всех частиц создает некий бозон.

Бозон Хиггса невозможно представить. Это точно не частица в форме шарика, как обычно рисуют электрон в учебнике. Представьте, что вы бежите по песку. Бежать ощутимо сложно, как будто бы увеличилась масса. Частицы пробираются в поле Хиггса и получают таким образом массу.

Объем тела

Объем — это физическая величина, которая показывает, сколько пространства занимает тело. Это важный навык — уметь объемы соотносить. Например, чтобы посчитать, сколько пластиковых шариков помещается в гигантский бассейн.

Например, чтобы рассчитать объем прямоугольного параллелепипеда, нам нужно перемножить три его параметра.

Формула объема параллелепипеда

V = a*b*c

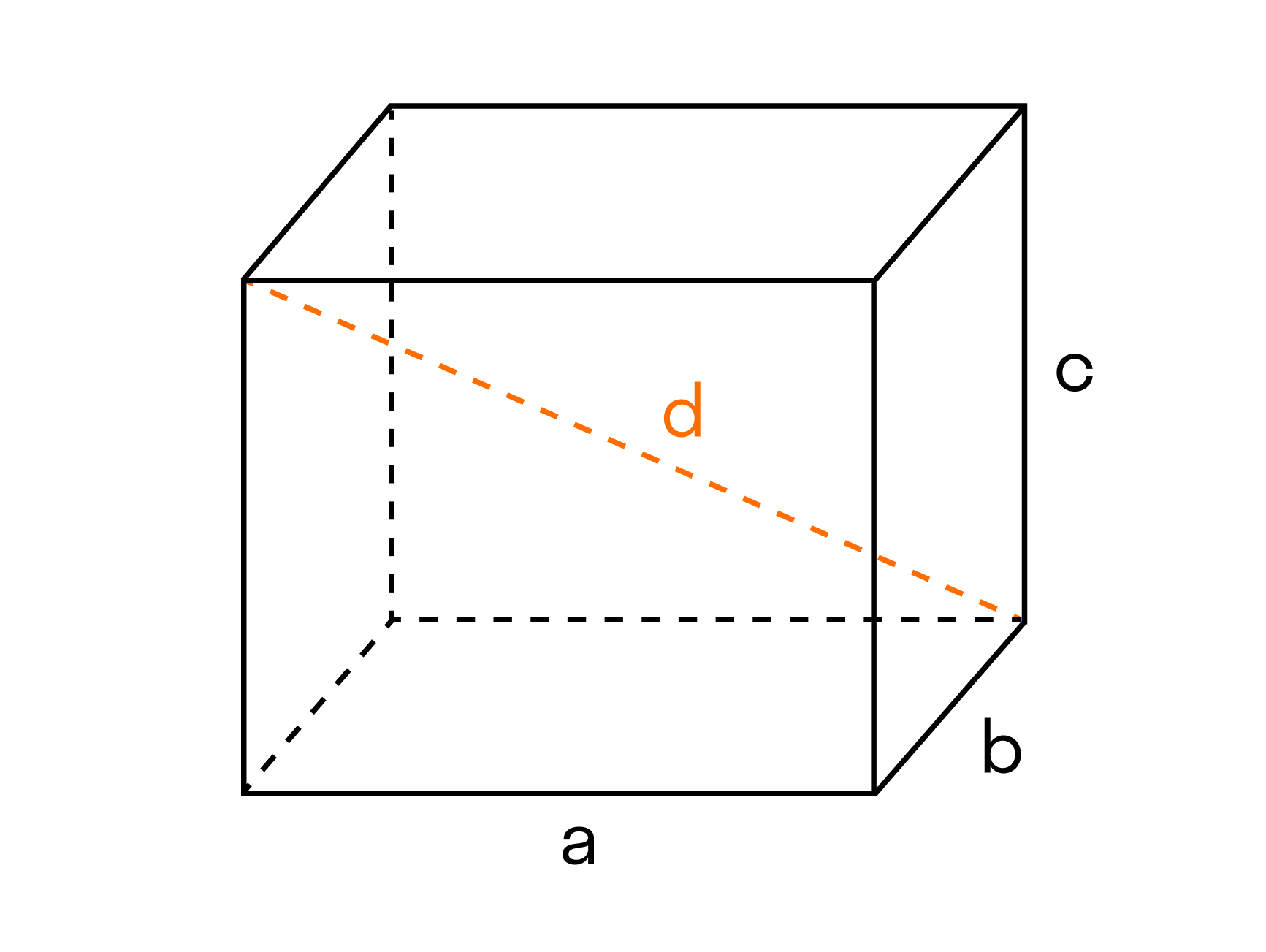
А для цилиндра будет справедлива такая формула:

Формула объема цилиндра

V = S*h

S — площадь основания [м^2]

Плотность вещества

Плотность — скалярная физическая величина. Определяется как отношение массы тела к занимаемому этим телом объёму.

Формула плотности вещества

р — плотность вещества [кг/м^3]

m — масса вещества [кг]

V — объем вещества [м^3]

Плотность зависит от температуры, агрегатного состояния вещества и внешнего давления. Обычно если давление увеличивается, то молекулы вещества утрамбовываются плотнее — следовательно, плотность больше. А рост температуры, как правило, приводит к увеличению расстояний между молекулами вещества — плотность понижается.

Ниже представлены значения плотностей для разных веществ. В дальнейшем это поможет при решении задач.

Источник

Окружающие тела состоят из веществ, масса каждого зависит от размера, объема и других критериев.

Плотность вещества показывает численное выражение массы тела в определенном объеме.

Существуют разные виды скалярной физической величины.

Общая характеристика

Каждый элемент занимает индивидуальную величину. Определение плотности может обозначаться греческой буквой ρ, D или d. Если объемы двух тел одинаковы, а массы различны, тогда плотности не идентичны.

Основные понятия

Определения и характеристики показателя известны с 7 класса школьной программы химии. Плотность представляет собой физическую величину о свойствах вещества. Это удельный вес любого элемента. Существует средняя и относительная плотность. Последняя классификация — это отношение плотности (П) вещества к П эталонного вещества. Часто за эталон принимают дистиллированную воду. Единица измерения П- кг/м3 в интернациональной системе.

Формула нахождения плотности:

Обозначения:

Кроме стандартной формулы плотности, применяемой для твердых состояний веществ, имеется формула для газообразных элементов в нормальных условиях.

Расшифровка:

Для сыпучих и пористых тел различают истинную плотность, вычисляемую без учета пустот, и удельную плотность, рассчитываемую как отношение массы вещества ко всему объему. Истинную П получают через коэффициент пористости — доли объема пустот в занимаемом объеме. Для сыпучих тел удельная П называется насыпной.

Низкие показатели П имеет среда между Галактиками (1033 кг/м3).

Способы измерения:

Вещества состоят из молекулярных структур, масса тела формируется из скопления молекул. Аналогично вес пакета с карамелью складывается из масс всех конфет в мешке. Если все сладости одинаковые, то массу упаковки определяют умножением веса одной конфеты на количество штук.

Молекулярные частицы чистого вещества одинаковы, поэтому вес капли воды равен произведению массы 1 молекулы Н2О на число составляющих молекул в капле. Плотность вещества показывает, чему равна масса одного кубического метра.

П льда составляет 900 кг/м³, это значит, что вес кубического метра льда равна 900 кг. Употребляют единицу измерения плотности г/см3.

При равнозначности физических масс двух тел их объемы различаются. Например, объём льда в девять раз больше объема бруска из металлического сплава. Масса тела распределяется неодинаково, устанавливает П в каждой точке тела.

Влияние факторов

П зависит от давления и температуры. При высоком давлении молекулы плотно прилегают друг к другу, поэтому вещество обладает значительной плотностью.

Зависимость показателей учитывается при расчете П. При повышении температуры П снижается из-за термического расширения, при котором объем вырастает, а масса остается прежней. Если температура снижается, П увеличивается, хотя имеются вещества, П которых при некоторых условиях температурного режима ведет себя иначе. Это вода, бронза, чугун. При фазовом переходе, модифицировании агрегатного состояния П меняется скачками. Условия вычисления зависят от свойств веществ, молекулярных элементов. Для разных природных объектов П изменяется в широком диапазоне.

П воды ниже П льда из-за молекулярной структуры твердой формы жидкости. Вещество, переходя из жидкой в твердую форму, изменяет молекулярную структуру, расстояние между составными частицами сужается и плотность увеличивается. Зимой, если забыть слить воду из труб, их разрывает на части после замерзания. На П Н2О влияют примеси. У морской воды знак П выше, чем у пресной. При соединении в одном стакане двух типов жидкости пресная останется на поверхности. Чем выше концентрация соли, тем больше П воды.

Когда плотность вещества больше П воды, оно полностью погрузится в воду. Предметы, сделанные из материала по низкой П, будут плавать на поверхности воды. На практике эти свойства используются человеком. Сооружая суда, инженеры-проектировщики применяют материалы с высокой П. Корабли, теплоходы, яхты смогут затонуть во время плавания, в корпусах суден создают специальные полости, наполненные воздухом, ведь его П ниже плотности воды.

Чтобы наживка для рыбалки погрузилась в воду, ее обременяют тяжелым по плотности материалом, например, грузиком из металла (чаще свинца). Плотность сплава выше, чем у Н2О.

Жирные пятна масла, нефти, бензина остаются на поверхности воды из-за низкой П маслянистых веществ.

Практическое применение

Из учебников химии и физики вычисляют уровень плотности по формуле. Но также это можно сделать, используя онлайн-систему.

Значение показателя

Окружающий мир состоит из разных веществ.

Скамейка в парке или баня за городом сооружены из древесины, подошва утюга, сковорода выполнены из металла, покрышка колеса, велосипеда — из резины. Каждый предмет имеет свой вес.

Черные дыры Вселенной составляют наибольшую плотность 1014 кг/м3. Самый низкий показатель имеет область между Галактиками (2•10−31—5•10−31 кг/м³).

Таблица плотности веществ

П металлов изменяется от минимального значения у лития, который легче Н2О, до максимального значения у осмия, который тяжелее драгоценных металлов.

Способы расчета и примеры

В сети Интернет существует множество приложений для онлайн-расчета плотности веществ или материалов. В стандартные поля калькулятора вводится основная информация: масса, объем, единицы измерения. Плотность вычисляется автоматически по заданным параметрам и выводится на экран интерфейса. Можно перевести информативные данные в нужную единицу измерения.

Без использования учебной информации показатель П можно определить через физические опыты. Для лабораторных изучений нужны весы, сантиметр, если исследуемое тело находится в твердом состоянии. Для жидкости необходима колба.

Сначала измеряют объем тела, записывая результат по цифровой шкале (в сантиметрах или миллилитрах).

Вычисляя объем деревянного бруска квадратной формы, параметр стороны возводится в третью степень. Измеряя объемные характеристики, тело ставят на весы и записывают значение массы. Рассчитывая жидкое состояние, учитывают массу сосуда, куда помещено исследуемое. В формулу подставляют данные и рассчитывают показатель.

Поскольку П измеряется в кг/л или в г/см³, то иногда приходится пересчитывать одни величины в другие.

Пример 1:

Пример 2:

Нужно перевести см 3 в кубические метры, а граммы — в килограммы.

Показатель имеет большое значение в разных сферах жизни и деятельности. Он определяется по таблице или высчитывается расчетным путем.

Источник

• ← Что такое до нашей эры 4 класс
• Что такое бритва триммер →