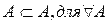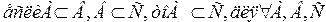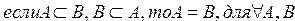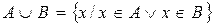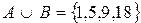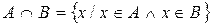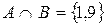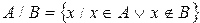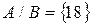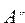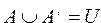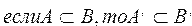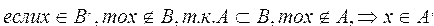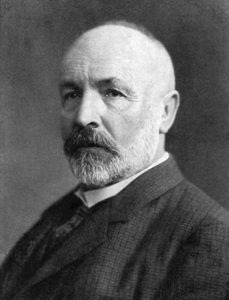Что такое подмножество в информатике

Множества

Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.

Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:

N — множество натуральных чисел,

Z — множество целых чисел.

Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.

Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись

означает, что множество L состоит из четырёх чётных чисел.

Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.

Подмножество

Подмножество — это множество, все элементы которого, являются частью другого множества.

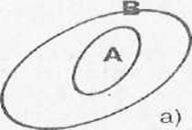
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.

Рассмотрим два множества:

Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂ :

Рассмотрим два множества:

Так как оба множества состоят из одних и тех же элементов, то L = M.

Пересечение и объединение множеств

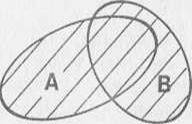
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.

При объединении равных множеств объединение будет равно любому из данных множеств:

Источник

Множество и его элементы. подмножество. пустое множество.

Понятие множества – одно из основных понятий математики. Под множеством понимают совокупность объектов (предметов или понятий), которая рассматривается как единое целое. Например, можно говорить о множестве натуральных чисел, о множестве букв на данной странице, о множестве корней данного уравнения и т. п. Понятие множества принимается как исходное, первичное, т. е. несводимое к другим понятиям. Объекты, входящие в состав множества, называются его элементами. Обычно множества обозначаются большими печатными буквами английского алфавита, например, множество А; а его элементы маленькими прописными буквами, например, элемент а.

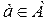
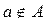
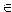
Запись означает, что элемент а принадлежит множеству А. Запись — наоборот, Что элемент а множеству А не принадлежит. Знак называют знаком принадлежности.

Определение 1. Два множества А и В называются равными и пишут А=В, если множества А и В содержат одни и те же элементы.

Например: <2, 4, 6>= <4, 2, 6>– равные множества.

Определение 2. Множество называется непустым, если содержит хотя бы один элемент.

Определение 3. Множество А является подмножеством множества В, если каждый элемент множества А принадлежит множеству В.

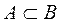
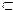
В этом случае пишут , знак называют знаком включения.

Например: <2, 4,>

Рассмотрим свойства отношения включения.

рефлексивно, т.е любое множество является подмножеством самому себе.

транзитивно, т. е. для любых множеств А, В и С, если множество А является подмножеством множества В и множество В является подмножеством множества С, то из этого следует, что множество А является подмножеством множества С.

антисимметрично, т. е. для любых множеств А и В следует, что, если множество А является подмножеством множества В и в то же время множество В является подмножеством множества А, то множества А и В равны.

Определение 4. Множество, не содержащее ни одного элемента, называется пустыммножеством.

Пустое множество обозначают

Пустое множество является подмножеством любого множества.

Определение 5. Множество всех подмножеств множества A называется множеством-степенью и обозначается P(A).

В дальнейшем будем пользоваться следующим утверждением:

Утверждение 1. Число всех подмножеств конечного множества равно 2n.

Пример. Выделим все подмножества множества А =<2, 4, 6>.

Р(А)=<2, 4, 6>, <2, 4>, <4, 6>, <2, 6>, <2>, <4 >, <6>, — всего 23=8.

Операции над множествами

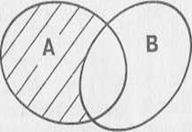
Объединением множеств А и В называется множество, состоящее из тех элементов, которые принадлежат одному из множеств А или В.

Для обозначения объединения множеств используют знак .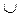

Пример. , ,

Пересечением множеств А и В называются такое множество, элементы которого принадлежат как множеству А, так и множеству В.

Для обозначения пересечения множеств используют знак .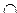

Пример. , ,

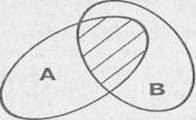
Разностью множеств А и В называется множество, элементы которого являются элементами множества А, не принадлежащие множеству В.

Для обозначения разности множеств используют знак /.

Пример. , ,

Перечислим основные свойства операций над множествами:

1) идемпотентность объединения

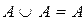
2) идемпотентность пересечения

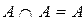
3) коммутативность объединения

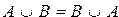
4) коммутативность пересечения

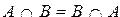
5) ассоциативность объединения

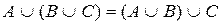
6) ассоциативность пересечения

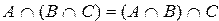
7) дистрибутивность объединения относительно пересечения

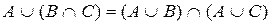
8) дистрибутивность пересечения относительно объединения

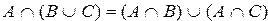
Универсальное множество. Дополнение множества.

Во многих приложениях теории множеств рассматриваются только такие множества, которые содержатся в некотором фиксированном множестве. Например, в геометрии мы имеем дело с множеством точек данного пространства, в арифметике – с множеством целых чисел. Такое фиксированное множество называют универсальным.Для его обозначения используют букву U.

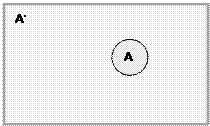
Определение 6. Множество U/А называется дополнением множества А и обозначается (или ).

Дополнение U/ множества обозначается

Справедливы следующие формулы:

=

— закон инволюции.

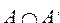
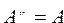
Теорема. Если множество А является подмножеством множества В, то дополнение множества А будет являться подмножеством дополнения множества В.

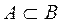
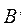
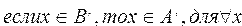
Пусть множество А является подмножеством множества В, , необходимо доказать, что для каждого элемента х из универсального множества U выполняется следующее условие: если элемент х принадлежит множеству , то он принадлежит и множеству .

.

Действительно, если х принадлежит множеству , то он не принадлежит множеству В, а т. к. множество А является подмножеством множества В, то элемент х не принадлежит и множеству А, а это означает его принадлежность множеству .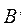

Теорема. Имеют место следующие тождества

— Законы де Моргана для множеств

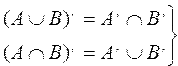
Приведем краткое доказательство первого утверждения.

Второе утверждение докажите самостоятельно.

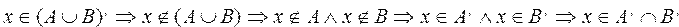
Для графического изображения множеств и их свойств используются так называемые диаграммы Эйлера-Венна.

Объединение множеств Пересечение множеств

Разность множеств Подмножество

Универсальное множество Дополнение

Понятие множества. Элементы множества. Пустое множество. Принадлежность элементов.

Источник

Информатика. 7 класс

Электронное приложение к учебному пособию

Напишите нам

белый — основные материалы, обязательные для изучения;

голубой — примеры, иллюстрирующие основные материалы;

желтый — определения основных понятий;

светло-зеленый — исторические сведения, информация об ученых, внесших вклад в развитие информатики, и другие интересные факты.

В учебном пособии используются следующие условные обозначения:

— вопросы и задания для проверки знаний;

— раздел «Упражнения» содержит задания, при выполнении которых используется компьютер;

— раздел «Упражнения» содержит задания для выполнения в тетради;

— раздел «Упражнения» содержит задания, при выполнении которых может быть использована информация, размещенная на Национальном образовательном портале;

* — задание или пример для любознательных.

§ 5. Множества

5.1. Понятие множества

Рассмотрим высказывание «Все учащиеся нашего класса имеют дома компьютер». Истинно оно или ложно? Для ответа на этот вопрос вам нужно задать каждому из одноклассников вопрос: «У тебя дома есть компьютер?» Если все учащиеся класса ответят утвердительно, то высказывание истинно, если хотя бы один из учащихся ответит «нет», то и высказывание будет ложным. Для разных классов это высказывание будет иметь различные значения, потому что различными будут множества учащихся класса.

Множество — совокупность каких-либо объектов, обладающих общим свойством. Эти объекты называют элементами множества.

Можно говорить о множестве учащихся 7 А класса, множестве отметок в классном журнале, множестве городов Беларуси, множестве букв русского алфавита и т. д. Понятие множества является одним из основных в математике.

Множества, как правило, обозначают прописными латинскими буквами, а элементы множества — строчными. Напомним, что для обозначения принадлежности элемента множеству используют специальные знаки:

Чтобы задать множество, необходимо перечислить его элементы (пример 5.1) или назвать их общее свойство (пример 5.2).

5.2. Понятие подмножества

Рассмотрим множество учащихся какого-либо класса. В этом множестве можно выделить не только отдельного учащегося, но и некоторые группы учащихся. Например, отличники, учащиеся, умеющие играть в теннис, изучающие французский язык и т. д. Каждая из таких групп образует подмножество — часть множества учащихся.

Если множество А является подмножеством множества М, то это записывают так:
А ⊂ М. Запись А ⊄ М обозначает, что множество А не является подмножеством множества М.

Подмножество может содержать все элементы множества, а может не содержать ни одного (пустое множество; обозначается знаком ∅).

Некоторые элементы множества могут принадлежать одновременно разным подмножествам (пример 5.3).

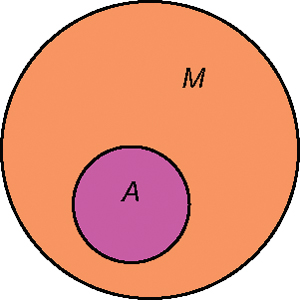
Для наглядной геометрической иллюстрации множеств и отношений между ними используют круги Эйлера. Каждое множество изображается кругом. Если какое-либо множество является подмножеством другого множества, то один круг изображается внутри другого. Например, если M — множество всех хищников, а A — множество всех львов ( A ⊂ M ), то это обозначается таким образом:

Множества, в том числе и бесконечные, в неявной форме использовались в математике со времен Древней Греции.

До XIX в. считалось, что точного определения множества нет. Множеством называли любое скопление, объединение предметов.

В конце XIX в. немецкий математик Георг Кантор (1845—1918) определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством».

Пример 5.1. Пусть множество M — это множество любимых учебных предметов семиклассника Игоря, состоящее из следующих элементов: математика, информатика, английский язык.

Тогда можно записать:

Пример 5.2. Пусть в множество M входят все учебные предметы, которые изучаются в 7-м классе. Перечислить все элементы данного множества можно, например, глядя на страницу школьного дневника.

Тогда можно записать:

Пример 5.3. Пусть М = <Вера, Сергей, Вася, Вика, Лиза, Костя, Надя>— множество учащихся 7 Б класса, занимающихся в драмкружке. Из этого множества можно выделить следующие подмножества:

А = <Вера, Вика, Лиза, Надя>— множество девочек (красная граница).

В = <Сергей, Вася, Костя>— множество мальчиков (синяя граница).

С = <Вера, Вася, Вика>— множество детей, чьи имена начинаются на букву «В» (зеленая граница).

D = <Вера, Сергей, Вася, Вика, Лиза, Костя, Надя>— множество детей, в именах которых по 2 гласных звука (желтая граница).

E = ∅ — множество трехлетних детей.

Леонард Эйлер (1707—1783) — ученый, внесший значительный вклад в развитие математики и механики, а также физики, астрономии и ряда прикладных наук.

1 Что понимают под множеством?

2 Что понимают под подмножеством?

3 Что используется для геометрической иллюстрации множеств?

Признаки: А — множество птиц, В — множество зверей;
2. мяч, стол, стул, коньки, шкаф, клюшка, шайба, комод;
3. сом, уж, карась, окунь, щука, гадюка, кобра, питон.

Источник

Понятие “Множество” в математике и информатике играет очень важную роль. В математике существует целая теория множеств.

Первое знакомство с данной темой может быть у учащихся как в начальной школе, если у них есть курс информатики, так и у учащихся 5-6 классов, которые раньше не изучали информатику. Данный материал подготовлен для учащихся 5-6 классов. Теме “Множества” желательно посвятить как минимум 2 урока. Материал может быть полезен и для преподавания информатики в начальной школе.

В курсе А.В. Горячева “Информатика в играх и задачах”, рассчитанного на учащихся начальной школы, тема “Множества” рассматривается и во 2 классе, и в 3 и в 4 классах. Естественно, что эта тема прорабатывается с детьми не один урок, а задания постепенно усложняются.

1. На первом уроке по теме “Множества” важно сразу же дать четкие определения тех терминов, которые потом будут использоваться в самых различных заданиях. Урок основан на использовании презентации (см. Приложение 1).

Множество произошло от слова “много”. Но в математике понятие “множество” используется более широко.

Множество может объединять любое количество предметов, чисел, существ. Каждый предмет множества называется элементом множества.

Множество, которое не содержит элементов, называется пустым.

Множество может иметь подмножества.

Множества могут пересекаться, не пересекаться, объединяться.

Равными называются множества, состоящие из одинакового числа одинаковых элементов.

(Желательно, чтобы эти определения были записаны учащимися в тетрадь, чтобы потом они могли к ним вернуться.)

Эти определения необходимо закрепить на простейших примерах, например: множество животных имеет несколько подмножеств: рыбы, птицы, звери, насекомые – и они не пересекаются. Если же мы возьмем множество морских животных, то оно будет пересекаться с множеством птиц и множеством зверей (приводятся несколько примеров). В качестве пустого множества можно дать такой пример: в яркий солнечный день на небе нет облаков, поэтому в этот день множество облаков (такое множество естественно существует) – пустое, а в другой день оно уже не будет пустым. Этот пример используется в тетради А.В. Горячева “Информатика в играх и задачах” 3 класс, часть 2. Можно привести и другие примеры, когда какое-то множество в конкретной ситуации будет пустым.

Также для удобства выполнения различных заданий необходимо ввести систему обозначения множеств (геометрические фигуры), подчеркнув, что это только условное обозначение, но оно очень удобно. Элементы множеств обозначаются точками.

Для закрепления понятия “элементы множества” учащимся предлагается следующее задание 1 (приложение 2) (его можно давать как домашнее задание, которое вклеивается в тетрадь).

2. Далее вводятся понятия, связанные с использованием логических связок в названиях множеств.

В названиях множеств и высказываниях могут употребляться логические связки: “и”, “не”, “или” и их комбинация: “не … и”, “не … или”. “не … и не …”

Если в названии множества есть связка “не”, то его элементы находятся за пределами фигуры, обозначающей это множество.

Если в названии множества есть связка “и”, то его элементы находятся на пересечении фигур, обозначающих множества.

Если в названии множества есть связка “или”, то это означает, что его элементы находятся в нескольких фигурах.

Эти схемы также необходимо закрепить с учащимися на разных примерах, включенных в задания в тетради (курс Горячева для начальной школы), а также на тех, где они сами приводят примеры различных множеств. Для закрепления понятий пересечения и объединения множеств учащимся предлагается дополнительное задание 2.

3. На следующем(их) уроке(ах) следует продолжить подробный разбор заданий, например, включив задания на пересечение трех множеств. (Желательно также, чтобы эти схемы были зарисованы учащимися в тетрадях).

При пересечении 2-х множеств образуется IV области: 2 области без пересечения, одна область пересечения множеств и одна область, лежащая за пределами выделенных множеств.

При пересечении 3-х множеств образуется VIII областей: 3 области без пересечения, 4 области пересечения множеств и 1 область, лежащая за пределами выделенных множеств.

При пересечении двух множеств закрашивается вся область пересечения этих множеств. При объединении двух множеств закрашиваются оба множества. При пересечении трех множеств закрашивается общая часть всех трех множеств. При отрицании всех трех множеств закрашивается область, не включающая в себя сами множества.

Данные схемы сделаны для задания, когда надо распределить слова, в состав которых входят буквы “С”, “Т” и “О”. Набор слов должен включать слова только с “Т”, только с “С”, только с “О”, а также одновременно с двумя и тремя буквами. Два-три слова должны быть без букв “С”, “Т”, “О”. (Например: рельсы, купе, проводник, скорость, колесо, электровоз, тамбур, вагон, сумка, место, шпалы, поезд, машинист, билет, состав, дверь, станция).

В курсе информатики А.В. Горячева в тетради 2 класса есть аналогичное задание на множества “Круглые”, “Желтые”, “Шары”.

Закрепление теоретического материала должно сопровождаться решением задач. Простейшие задачи, например, “Про коз и коров”, “Фиалки и подруги”, “Газеты и журналы” могут быть использованы даже во 2 классе (см. приложение 4). Для более сильных учеников и для более старших классов, соответственно, можно подобрать задачи нужного уровня, а можно также использовать какие-то задачи и для проведения конкурсов, КВНов, школьных олимпиад, недели математики и информатики. Подобные задачи удобно решать, используя схему множеств и обозначая элементы просто точками (если числа малые) или указывая число элементов в соответствующей области (в пересечении, без пересечения).

Источник