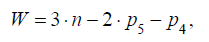Что такое подвижность механизма
Степень подвижности механизмов
Составив кинематическую схему механизма и определив число подвижных звеньев, число и типы кинематических пар, необходимо определить степень подвижности механизма.
Подвижность кинематической цепи – это определенность движения звеньев по отношению к одному из них – неподвижному звену, именуемому стойкой. Определенность движения звеньев предполагает строгую повторяемость их траекторий движения и является обязательным свойством кинематической цепи любого реального устройства, так как в противном случае управление устройством невозможно.
За обобщенную координату в плоских механизмах, как правило, принимают угол поворота входного звена φ и следовательно, если задавать ее изменение во времени, то можно получить вполне определенное движение звеньев такой кинематической цепи, называемой механизмом. Таким образом, количество входных звеньев определяется степенью подвижности механизма.
Понятие о степенях подвижности относится не к реальным механизмам, а к их идеализированным моделям. Идеализация состоит в том, что звенья механизма, являющиеся твёрдыми телами, считают абсолютно твёрдыми, жидкие звенья – несжимаемыми, гибкие – нерастяжимыми. Соединения звеньев (кинематические пары) также принимают идеальными (отсутствие зазоров в шарнирах, качение без скольжения во фрикционных передачах и т.п.). Для такого идеального механизма понятие «степень подвижности» равносильно принятому в теоретической механике понятию «число степенейсвободы». (Числом степеней свободы является число независимых параметров, однозначно определяющих положение всех звеньев механизма в пространстве либо на плоскости).
Степень подвижности плоских механизмов определяется по формуле П.Л. Чебышева:
где: W – степень подвижности механизма;
n – число подвижных звеньев механизма;
Р5 – число кинематических пар пятого класса;
Р4 – число кинематических пар четвёртого класса.
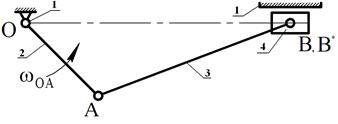
В кривошипно-ползунном механизме (Рис. 5) три подвижных звена:кривошип – 2, шатун – 3, ползун – 4 и три кинематические пары пятого класса: вращательные – О(1-2), А(2-3), В(3-4), и поступательная пара В * (4-1) т.е.n=3;Р5=4;Р4=0.
Рис.5 Схема кривошипно-ползунного механизма.
По формуле (1) получаем: W=l. В данном механизме одно входное звено.
1.8 Структурная классификация механизмов
Структурной классификацией механизмов называется разделение их на группы и классы по общности структуры.
Впервые научно обоснованная, рациональная классификация плоских механизмов была предложена в 1914 году русским учёным Л.В. Ассуром. Дальнейшее развитие структурная классификация плоских механизмов получила в работах И.И. Артоболевского.
Классификация механизмов по Ассуру-Артоболевскому позволяет для механизмов, отнесённых к одному и тому же классу, применять методику кинематического и силового анализа, разработанную специально для этого класса механизмов.
Согласно этой классификации, механизм может быть образован путём присоединения к начальному звену (или начальным звеньям) и стойке некоторых кинематических цепей.
Каждое начальное звено, входящее в кинематическую пару со стойкой (вращательную или поступательную) условно называют начальным механизмом. Начальный механизм принято считать механизмом первого класса и первого порядка.
Кинематические цепи, обладающие нулевой подвижностью относительно внешних кинематических пар и не распадающиеся на более простые цепи, удовлетворяющие этому условию, называются структурными группами Ассура.
Структурные группы Ассура не влияют на подвижность механизма, они изменяют его структуру и законы движения звеньев.
В группы Ассура входят только низшие кинематические пары, поэтому степень подвижности группы определится по формуле:
Отсюда следует, что зависимость числа кинематических пар Р5 от числа звеньев n имеет вид:
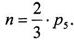
Чтобы из механизма выделить структурные группы, необходимо помнить их основные признаки, вытекающие из определения:
а) число звеньев в группе Ассура должно быть чётным, а число кинематических пар кратно трём, (Табл.3)
Таблица 3. Соотношение числа звеньев и числа кинематических пар в группах Ассура
б) степень подвижности группы всегда равна нулю;
в) степень подвижности оставшейся части механизма при отсоединении групп Ассура не должна изменяться.
Дата добавления: 2018-03-01 ; просмотров: 8851 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Определение степени подвижности механизма



Определение степени подвижности пространственной кинематической цепи
Пусть мы имеем n звеньев, из которых собирается кинематическая цепь. Пока звенья не соединены в кинематические пары, каждое из них имеет шесть степеней свободы (степеней подвижности). Все звенья до соединения в кинематическую цепь следовательно имели 6n степеней подвижности. После сборки звеньев в кинематическую цепь мы получим кинематические пары различных классов (с разными степенями подвижности). Предположим, что наша кинематическая цепь имеет кинематические пары всех пяти классов.
Примем следующие обозначения:
Степенью подвижности механизма называется количество независимых координат, которые необходимо задать для определения положений звеньев механизма в системе координат, жестко связанной со стойкой.
Механизм отличается от кинематической цепи тем, что у него одно звено полностью закреплено. Закрепленное звено потеряло все шесть степеней свободы. Следовательно в механизме число подвижных звеньев равно n-1. Подставив в формулу (1) количество подвижных звеньев n-1, получим формулу для определения степени подвижности механизма:
Формула (2) впервые была получена Малышевым для пространственных механизмов.
Рассмотрим формулу Малышева для определения степени подвижности плоских механизмов. Все звенья плоского механизма могут иметь три степени подвижности, а кинематические пары соответственно могут иметь 1 или 2 степени подвижности. Если плоские кинематические пары рассматривать по классам, то они могут быть только пятого и четвёртого классов. При этом необходимо учесть, что общее количество степеней подвижности всех звеньев плоского механизма равно 3(n-1). Пары пятого класса теряют две степени подвижности, четвёртого –одну. Таким образом степень подвижности плоского механизма может быть определена по формуле:
Формула (3) для определения степени подвижности плоского механизма впервые была получена Чебышевым П. Л.
В зависимости от числа общих условий связей, накладываемых на механизм, механизмы подразделяют на семейства.
Семейства механизмов и их структурные формулы приведены в таблице 1.
Таблица 2.1 Структурные формулы различных семейств механизмов
| Семейство | Структурная формула | Примечание |
| I II III IV | W=6(n-1)-5P5-4Р4-3Р3-2Р2-1P1 W=5(n-1)-4P5-3Р4-2Р3-Р2 W=4(n-1)-3P5-2Р4-Р3 W=3(n-1)-2P5-Р4 W=2(n-1)- P5 | Сомова-Малышева Чебышева Добровольского |
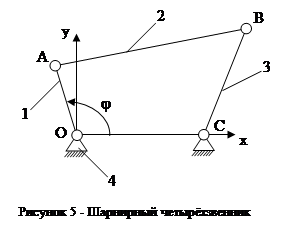
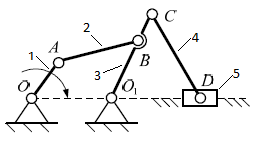
Рассмотрим применение структурной формулы Чебышева П. Л. на конкретном примере. На рисунке 5 изображен шарнирный четырёхзвенник.
Количество звеньев n = 4. Кинематические пары: 4-1, 1-2, 2-3, 3-4. Имеем 4 одноподвижные пары 5 го класса. Относительное движение всех звеньев плоское. Механизм плоский. Определяем степень подвижности его по формуле Чебышева П. Л.:
Механизм имеет степень подвижности равную 1. Это значит, что достаточно задать одну координату любому звену механизма в системе координат, жестко связанной со станиной, чтобы определить положения всех остальных звеньев. Например, в нашем случае достаточно задаться углом поворота кривошипа j1.
Пассивные связи и избыточные звенья
Звенья и кинематические пары, которые не влияют на характер движения механизма в целом, называются избыточными (лишними) звеньями и парами, а обусловленные ими связи называются пассивными связями.
При определении степени подвижности механизма избыточные звенья и кинематические пары не должны учитываться.
В сложных стержневых механизмах не всегда на глаз можно определить степень подвижности. В этих случаях необходимо воспользоваться формулой Чебышева.
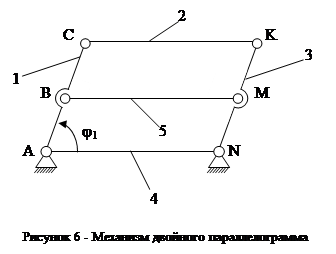
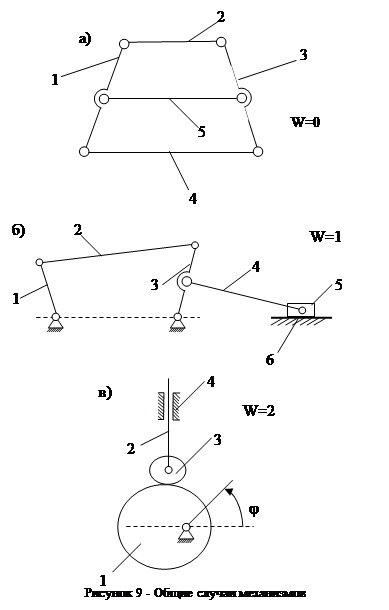
Если W=0, то должен быть не механизм, а жесткая ферма. Мы видим, что механизм может осуществлять движение. Если в этом механизме мысленно убрать звено 5 (или 2), то при этом характер движения остальных звеньев останется неизменным. Механизм превращается в обычный четырёхзвенник, W которого мы уже определили – W=1. При устранении звена 5 одновременно устраняется 2 кинематические пары: 5-1, 5-3. Следовательно, в этом механизме избыточными является одно звено и две кинематические пары.
Определим W по формуле Чебышева:
По схеме механизма видно, что он будет работать и W=1.
Пусть отсутствует непосредственное соединение звеньев 2-3. Звенья 3, 4, 5 всё равно займут положение, соответствующее углу поворота j1 звена 1, т. к. звенья 1, 2, 4 должны быть зафиксированы этим углом. То же самое можно получить, если удалить кинематическую пару 2-4 или 4-3. Здесь одна кинематическая пара избыточная. Её можно не учитывать. Тогда:
При этом замечаем, что устранение звена влечёт за собой устранение некоторых кинематических пар. Устранение кинематических пар (прекращение контакта звеньев) не влечёт за собой как неизбежное устранение входящих в неё звеньев.
Соединение звеньев, где соединяется 3 и более звеньев, называется узлом. В узле на одну кинематическую пару меньше, чем звеньев.
Избыточные кинематические пары и звенья накладывают дополнительные условия на точность изготовления механизма, однако несмотря на это в механизм вводят иногда пассивное звено или лишнюю связь с целью получения каких либо дополнительных необходимых качеств; увеличение прочности, уменьшение трения и др.
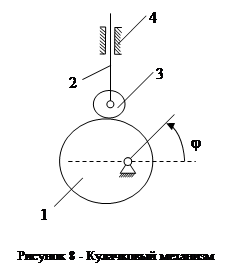
Определим W кулачкового механизма, изображенного на рисунке 2.8. Здесь звенья 1- кулачок, 2- толкатель, 3- ролик, 4- стойка. Количество звеньев n=4. Кинематические пары 1-4, 2-4, 2-3 пятого класса и 3-1 – высшая плоская кинематическая пара 4 го класса. При повороте кулачка на угол j толкатель займёт определённое положение. На первый взгляд W=1.
Определим W по формуле Чебышева:
Здесь есть лишняя степень подвижности. Если бы ролик неподвижно закрепить с толкателем, то W механизма была бы равна единице. Поворот ролика по отношению к остальным звеньям не оказывает никакого влияния. Угол поворота ролика- это и есть лишняя степень свободы механизма.
Лишней степенью свободы называется такая степень свободы в движении некоторых звеньев, устранение которой не вызывает изменений в характере движения других звеньев по кинематическим соображениям.
При этом имеется в виду абсолютное или относительное движение звена. Устранение лишней степени свободы не влечёт за собой устранение звена.
Прежде чем пользоваться формулой Чебышева необходимо мысленно исключать из рассмотрения пассивные связи и лишние степени свободы.
Формула Чебышева в общем случае даёт правильный ответ. В общих случаях пассивные связи и лишние степени свободы не существуют и могут быть только в частных случаях.
Например: механизм двойного параллелограмма является частным случаем такого же механизма, когда звенья не параллельны (рисунок 9а); механизм Маркуса является частным случаем механизма, когда оси шарнирных соединений звеньев 2, 4 не совпадают (рисунок 9б); круглый ролик является более частным случаем геометрической формы ролика не круглой формы (рисунок 9в).
Таким образом формула Чебышева даёт возможность выявить характерные особенности (частности) механизмов.
ОПРЕДЕЛЕНИЕ ПОДВИЖНОСТИ И МАНЕВРЕННОСТИ МЕХАНИЗМА
ЕВРАЗИЙСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ
КАФЕДРА КОСМИЧЕСКАЯ ТЕХНИКА И ТЕХНОЛОГИИ
КУРСОВАЯ РАБОТА
ПО ДИСЦИПЛИНЕ ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
Выполнила: Барлыбаева А. А.
Студентка группы КТиТ-22
2 курса специальности
Космическая техника и технологии
СОДЕРЖАНИЕ
2. СТРУКТУРНЫЙ АНАЛИЗ ПЛОСКИХ МЕХАНИЗМОВ…………………………..………4
3. ОПРЕДЕЛЕНИЕ ПОДВИЖНОСТИ И МАНЕВРЕННОСТИ МЕХАНИЗМА……………..9
4. МЕТРИЧЕСКИЙ СИНТЕЗ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ………………. 12
5. КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКИХ РЫЧАЖНЫХ МЕХАНИЗМОВ…………..16
ВВЕДЕНИЕ
Теория механизмов и машин (ТММ) – это дисциплина, изучающая общие методы проектирования и исследования механизмов и машин. Данная дисциплина является составной частью общеинженерной дисциплины «Механика», закладывающей основы понятия об инженерном проектировании[1].
Инженерноепроектирование – это процесс, в котором научная и техническая информация используется для создания новых или модернизации уже существующих механизмов и машин, приносящих обществу определенную пользу. Проектирование– этопроцесс составления описания, необходимого для создания еще несуществующего объекта путем преобразования первичного описания, оптимизации заданных характеристик объекта, устранения некорректности первичного описания и последовательного представления описаний на различных языках[5].
Специфика дисциплины «Теория механизмов и машин» заключается в том, что вместо общепринятых понятий, таких, как исследование и проектирование, соответственно, используются термины анализ и синтез. При этом под анализом подразумевается исследование или изучение, а под синтезом – проектирование или создание механизмов и машин[5].
Цель ТММ – анализ и синтез типовых механизмов и машин, а также систем, созданных на их основе[5].
Задача ТММ – разработка общих методов синтеза и анализа структуры, кинематики и динамики типовых механизмов и машин, а также систем, созданных на их основе[5].
СТРУКТУРНЫЙ АНАЛИЗ ПЛОСКИХ МЕХАНИЗМОВ
Теоретическое обоснование
Структурный анализ – это процесс исследования структуры механизма, т.е. определение числа звеньев и видов движения, ими совершаемых, числа и вида кинематических пар, структурных групп и кинематических цепей, числа подвижностей и наличия дефектов[1].
Структурный анализ механизмов проводится с целью выявления дефектов их структуры, которые при необходимости устраняются[1].
В общем случае структурный анализ плоских механизмов сводится к решению следующих задач[5]:
1) определение подвижности механизма;
2) анализ состава структуры механизма.
Подвижность механизма – это число независимых обобщенных координат, однозначно определяющих положения звеньев механизма на плоскости или в пространстве в рассматриваемый момент времени[2].
Механизм любой сложности может быть представлен в виде начального механизма (состоящего из стойки и входного звена) и присоединенных к нему структурных групп (групп Ассура)[1].
Структурная группа – это плоская элементарная кинематическая цепь, состоящая из низших кинематических пар и имеющая нулевую подвижность по отношению к системе, к которой она присоединяется (Wгр = 0 в присоединенном состоянии)[1].
Задача 1. Вариант 1
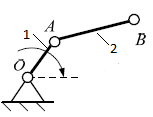
Выполнить структурный анализ кривошипно-ползунного механизма (рис.1).
Рис.1 Схема кривошипно-ползунного механизма
Решение.Схема кривошипно-ползунного механизма представляет собой замкнутую кинематическую цепь, следовательно, данный механизм является плоским механизмом. В этом случае структурный анализ кривошипно-ползунного механизма сводится к решению двух задач:
1) определению подвижности механизма;
2) определению состава структуры.
Рассмотрим каждую задачу в отдельности.
Подвижность кривошипно-ползунного механизма определяется по структурной формуле Чебышева
где р4, р5 – количество кинематических пар четвертого и пятого классов, n – количество подвижных звеньев кинематической цепи.
Структурная схема рассматриваемого механизма состоит из пяти звеньев:
1 – звено ОА– кривошип,
3 – звено O1С– кривошип,
При этом звенья 1 – 5 являются подвижными звеньями, а стойка Ои О1 представлена в структурной схеме шарнирно-неподвижными опорами и являются неподвижными звеньями. Следовательно, n = 5. Для определения значений коэффициентов p4 и p5 выявим все кинематические пары, входящие в состав схемы механизма. Результаты анализа заносим в табл.1.1.
| № п/п | Номера звеньев/название | Схема | Класс/подвижность | Вид контакта/замыкание |
| 1 | 0 – 1/ вращательная |  | 5/1 | Поверхность(низшая)/ геометрическое |
| 2 | 1 – 2/ вращательная | 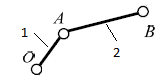 | 5/1 | Поверхность(низшая)/ геометрическое |
| 3 | 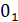 – 3/ Вращательная – 3/ Вращательная | 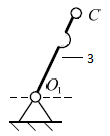 | 5/1 | Поверхность(низшая)/ геометрическое |
| 4 | 2 – 3/ вращательная | 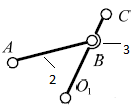 | 5/1 | Поверхность(низшая)/ геометрическое |
| 5 | 3 – 4/ вращательная | 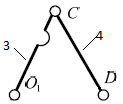 | 5/1 | Поверхность(низшая)/ геометрическое |
| 6 | 4 – 5/ вращательная | 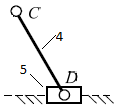 | 5/1 | Поверхность(низшая)/ геометрическое |
| 7 | 0 – 5/ поступательная | 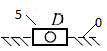 | 5/1 | Поверхность(низшая)/ геометрическое |
Из анализа данных табл. 1.1 следует, что исследуемая схема кривошипно-ползунного механизма представляет собой замкнутую кинематическую цепь, звенья которой образуют между собой семь пар пятого класса. Следовательно, р5 = 7,а р4 = 0.
Подставив найденные значения коэффициентов в структурную формулу Чебышева, получим
W = 3*5 − 2 * 7 − 0 = 15 − 14 =1
Состав структуры кривошипно-ползунного механизма исследуем согласно принципу построения механизмов по Ассуру.
Начиная с выходного звена – ползуна 5, разбиваем рассматриваемую
схему кривошипно-ползунного механизма на группы звеньев.
Группа звеньев 0 – 5 – 4
Подставив выявленные значения коэффициентов в структурную формулу Чебышева, получим
Следовательно, группа звеньев является структурной группой 2-го класса 2-го порядка 2-го вида, структурная формула которой имеет вид ВВП.
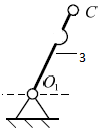
Группа звеньев 01 – 3
Данная группа звеньев состоит из подвижного звена– кривошипа 3,стойки 01, образующих одну кинематическую пару пятого класса; 01 – 3 – вращательная пара, тогда
Подставив выявленные значения коэффициентов в структурную формулу Чебышева, получим
Группа звеньев 01 – 3 не является структурной группой, а представляет собой первичный механизм.
Группа звеньев 0 – 1 – 2
Данная группа звеньев состоит из двух подвижных звеньев – шатуна2, кривошипа 1и стойки 0, образующих три кинематические пары пятого класса; 0 – 1, 1 – 2 – вращательная пара, тогда n = 2,р5 = 3, а р4 = 0.
Подставив выявленные значения коэффициентов в структурную формулу Чебышева, получим
Следовательно, группа звеньев является структурной группой 2-го класса 2-го порядка 2-го вида, структурная формула которой имеет вид ВВП.
Вывод.
ОПРЕДЕЛЕНИЕ ПОДВИЖНОСТИ И МАНЕВРЕННОСТИ МЕХАНИЗМА
Теоретическое обоснование
Степенью подвижности механизма называется количество независимых координат, которые необходимо задать для определения положений звеньев механизма в системе координат, жестко связанной со стойкой[5].
Механизм отличается от кинематической цепи тем, что у него одно звено полностью закреплено. Закрепленное звено потеряло все шесть степеней свободы. Следовательно в механизме число подвижных звеньев равно n-1. Подставив в формулу (1) количество подвижных звеньев n-1, получим формулу для определения степени подвижности механизма[1]:
Степень подвижности механизма определяет число ведущих его звеньев, т.е. количество звеньев, которым необходимо задать движение, чтобы все остальные звенья двигались по вполне определенным законам[5].
Маневренность – это число степеней подвижности механизма при неподвижном (фиксированном) положении выходного звена, подведенного к данной точке. Маневренность зависит не только от вида и числа кинематических пар, но и от их расположения. Под манипулятивностью понимается способность занимать различную ориентацию выходным звеном в заданной точке конфигурационного пространства. Для определения маневренности необходимо остановить выходное звено[1].
Задача 2. Вариант 1
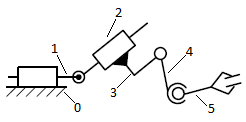
Определить подвижность и маневренность механизма (рис. 2).
Рис. 2 Схема механизма
Решение.
1)Проанализируем схему механизма (рис. 2), выходное звено 5 которого со стойкой 0 не образует кинематических пар, следовательно, схема рассматриваемого механизма является незамкнутой кинематической цепью. Подвижность определяется по формуле Сомова–Малышева.
Для определения значений коэффициентов p1, p2, p3, p4 и p5 выявим все кинематические пары, входящие в состав схемы механизма промышленного манипулятора. Результаты исследования заносим в табл. 2.1
| № п/п | Номера звеньев /название | Схема | Класс/подвижность | Вид контакта/ замыкание |
| 1 | 0-1/ неподвижная | 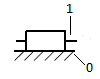 | ||
| 2 | 1-2/ вращательная |  | 5/1 | Поверхность(низшая)/геометрическое |
| 3 | 2-3/ поступательная | 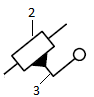 | 5/1 | Поверхность(низшая)/геометрическое |
| 4 | 3-4/ вращательная | 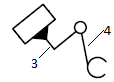 | 5/1 | Поверхность(низшая)/геометрическое |
| 5 | 4-5/ сферическая | 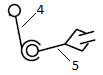 | 3/3 | Поверхность(низшая)/геометрическое |
Из анализа данных табл. 2.1 следует, что исследуемая схема механизма манипулятора промышленного робота представляет собой разомкнутую кинематическую цепь, звенья которой образуют между собой три пары пятого класса: 1 – 2, 2 – 3, 3 – 4 и одну сферическую пару третьего класса: 4 – 5. Следовательно, p5= 3, p4=0, p3=1, p2=0, p1=0.
Подставив найденные значения коэффициентов в структурную формулу Сомова–Малышева получим
n – число подвижных звеньев, р5 – 5 класса, р4 – 4 класса, р3 – 3 класса, р2 – 2 класса.
W = 6 · 4− 5 · 3− 4 · 0 − 3 ·1− 2 · 0 − 0 = 24 – 15 – 3= 6.
Результат свидетельствует о том, что для однозначного описания положений звеньев механизма манипулятора промышленного робота в пространстве необходимо семь обобщенных координат.
2) Маневренность – это подвижность пространственного механизма при неподвижном звене 5. Маневренность обозначают m и определяют по формуле Сомова–Малышева.
Для определения маневренности необходимо остановить (запретить перемещаться) выходное звено. Следовательно, число подвижных звеньев становиться равным трем, т. е. n = 3. Значения всех остальных коэффициентов не изменяются, т. е. p5 = 3, p4 = 0, p3 = 1, p2 = 0, p1 = 0.
Подставив найденные значения коэффициентов в выражение для маневренности, получим
m = 6 · 3 − 5 · 3− 4 · 0 − 3 ·1− 2 · 0 − 0 = 18− 15− 3=0
Результат говорит о том, что для однозначного определения положений звеньев механизма манипулятора промышленного робота, имеющего замкнутую кинематическую цепь, достаточно одной обобщенной координаты. Проверим полученное значение
Вывод.Расчет по обоим выражениям дает одинаковое значение маневренности, которое удовлетворяет условию работоспособности пространственного рычажного механизма, гласящему, что маневренность должна быть больше либо равна единице. Также определили подвижности и маневренности механизма:количества подвижных звеньев n; количества кинематических пар, входящих в его состав р; подвижности каждой кинематической пары S;степени подвижности механизма W; маневренность m.
Дата добавления: 2018-06-01 ; просмотров: 2725 ; Мы поможем в написании вашей работы!