Что такое погрешность округления
Приложение А. Погрешности вычислений
Абсолютная и относительная погрешности
Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.
Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:
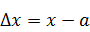
где а – приближенное значение числа х.
Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:
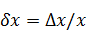
Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность 

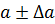
Источники погрешностей
Рассмотрим различные причины возникновения погрешностей.
Математическая модель задачи является неточной
Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций).
Ошибки в исходных данных
Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения.
Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений.
Вычислительные ошибки (ошибки округления)
Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы.
Вычислительные ошибки
Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно.
Представление чисел с плавающей точкой
Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от 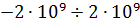
В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок:
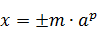
где m – мантисса, p – порядок, а – основание степени.
Например, число 273.9 можно 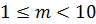
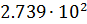
В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности.
| Точность | Одинарная | Двойная |
| Размер (байты) | 4 | 8 |
| Наименьшее значение | 1.2·10 −38 | 2.3·10 −308 |
| Наибольшее значение | 3.4×10 +38 | 1.7×10 +308 |
| Размеры степени и мантиссы (биты) | 8-23 | 11-52 |
Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой
Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что 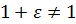
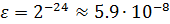
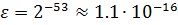
Погрешность округления
При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность 
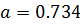
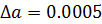
Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например:
Погрешность арифметических действий над приближенными числами
При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются:
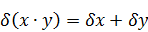
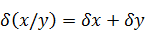
При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени:
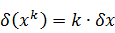
При сложении или вычитании чисел их абсолютные погрешности складываются:
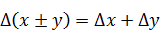
Относительная погрешность суммы положительных слагаемых вычисляется как:
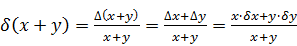
Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых:
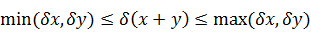
На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность 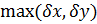
При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению:
1234 + 0.005678 = 1234.00005678
или в компьютерном представлении:
1.234Е+03 + 5.678Е-03 = 1.234005678Е+03
После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении.
Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях 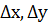
Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются.
Правила округления. Обработка и представление результатов измерений. Процедура
Обработка и представление результатов измерений. Процедура
1. Назначение и область применения
1.1. Процедура устанавливает единые требования к обработке и представлению результатов измерений, полученных в лаборатории (центре).
1.2. Представление результатов измерений в лабораторных журналах и в документах, выдаваемых лабораторией, осуществляется согласно методикам измерений и данной процедуре.
1.3. Требования настоящей процедуры распространяются на всех специалистов лаборатории (центра).
2. Нормативные ссылки
2.1. СТ СЭВ 543-77 «Числа. Правила записи и округления» (настоящий стандарт является обязательным в рамках Конвенции о применении стандартов СЭВ);
2.2. ГОСТ 8.736-2011 «Государственная система обеспечения единства измерений (ГСИ). Измерения прямые многократные. Методы обработки результатов измерений. Основные положения»;
2.3. МР 18.1.04-2005 «Система контроля качества результатов анализа проб объектов окружающей среды»;
2.4. ПМГ 96-2009 «Государственная система обеспечения единства измерений (ГСИ). Результаты и характеристики качества измерений. Формы представления» (правила по межгосударственной стандартизации введены в действие для добровольного применения в РФ в качестве рекомендаций по метрологии РФ).
Примеры
1) Число 12,0 – имеет три значащие цифры;
2) Число 30 – имеет две значащие цифры;
3) Число 120 × 10 3 – имеет три значащие цифры;
4) Число 0,514 × 10 – имеет три значащие цифры;
5) Число 0,0056 × 10 – имеет две значащие цифры;
6) Число 0,704 – имеет три значащие цифры;
7) Число 68 – имеет две значащие цифры.
Таким образом, нули вначале числа всегда незначимы; нули в середине числа между ненулевыми цифрами значимы; нули в конце числа могут быть значимыми и незначимыми.
По количеству значащих цифр осуществляется запись приближенных чисел (согласно СТ СЭВ 543-77).
Пример
Следует различать числа 2,4 и 2,40.
Запись 2,4 означает, что верны только цифры целых и десятых; истинное значение числа может быть, например, 2,43 и 2,38.
Запись 2,40 означает, что верны и сотые доли числа; истинное число может быть, например, 2,403 и 2,398, но не 2,421 и не 2,382.
3.2. Округление числа – это отбрасывание значащих цифр справа до определенного разряда с возможным изменением цифры этого разряда (согласно СТ СЭВ 543-77).
В случае, если первая из отбрасываемых цифр (считая слева направо) меньше 5, то последняя сохраняемая цифра не меняется.
В случае, если первая из отбрасываемых цифр (считая слева направо) равна или больше 5, то последняя сохраняемая цифра увеличивается на единицу.
Округление следует выполнять сразу до желаемого числа значащих цифр, поэтапное округление может привести к ошибкам.
Примеры
1) Если число 12,364 требуется округлить до сотых долей, после округления получаем число 12,36; если число 12,364 требуется округлить до десятых долей, после округления получаем число 12,4.
2) Если число 0,703 требуется округлить до сотых долей, получаем число 0,70; если число 0,703 требуется округлить до десятых долей, после округления получаем число 0,7.
3) Если число 0,703 требуется округлить до двух значащих цифр, после округления получаем число 0,70; если число 0,703 требуется округлить до одной значащей цифры, после округления получаем число 0,7.
4) Если число 0,429 требуется округлить до двух значащих цифр, после округления получаем число 0,43; если число 0,429 требуется округлить до одной значащей цифры, после округления получаем число 0,4.
5) Если число 8,574 требуется округлить до двух значащих цифр, после округления получаем число 8,6; если число 8,574 требуется округлить до одной значащей цифры, после округления получаем число 9.
6) Поэтапное округление результата измерения 227,46 дает на первом этапе 227,5 и на втором этапе 228, в то время как правильный результат округления 227.
3.3. Окончательный результат – это результат измерения с погрешностью, который вносится испытателями в лабораторные журналы. Окончательный результат выдается лабораторией в протоколе испытаний.
3.4. Промежуточные результаты – это вся информация по анализу от показания приборов до окончательного результата (в том числе расчеты результатов единичных определений; расчет результата измерения как среднеарифметическое значение результатов единичных определений, полученных в условиях повторяемости; контроль повторяемости; расчет погрешности). Промежуточные результаты заносятся испытателями в лабораторные журналы, но в протоколах испытаний не выдаются.
4.1. Требования к промежуточному результату
4.1.1. Число значащих цифр в промежуточных вычислениях при обработке результатов измерений должно быть больше, чем в окончательном результате.
4.1.2. Если значение погрешности (неопределенности) результата измерений представлено числом, содержащим две значащие цифры, то для промежуточных результатов расчета сохраняем не менее трех значащих цифр.
4.1.3. Если значение погрешности (неопределенности) результата измерений представлено числом, содержащим одну значащую цифру, то для промежуточных результатов расчета сохраняем не менее двух значащих цифр.
4.1.4. При проведении промежуточных расчетов в рукописных лабораторных журналах в числовых значениях измеряемой величины и погрешности следует оставлять столько значащих цифр, чтобы в окончательном результате не появлялась ошибка, связанная с поэтапным округлением.
Примеры
| Промежуточные результаты | Окончательные результаты |
| 0,178 ± 0,053 | 0,18 ± 0,05 |
| 0,1784 ± 0,0533 | 0,178 ± 0,053 |
| 1,22 ± 0,18 | 1,2 ± 0,2 |
| 1,224 ± 0,183 | 1,22 ± 0,18 |
| 3,74 ± 0,748 | 3,7 ± 0,7 |
| 3,742 ± 0,748 | 3,74 ± 0,75 |
| 12,83 ± 1,28 | 12,8 ± 1,3 |
| 54,2 ± 5,4 | 54 ± 5 |
| 54,23 ± 5,42 | 54,2 ± 5,4 |
| 177,6 ± 33,7 | 178 ± 34 |
| 2357,4 ± 212,2 | 2357 ± 212 |
| 11624,8 ± 5812,4 | 11624 ± 5812 |
4.2. Требования к окончательному результату
4.2.1. Числовые значения результата измерений и его погрешности (неопределенности) записываются с указанием одной и той же единицы измерения.
Примеры
(5,4 ± 0,5) мг/дм³;
(6,1 ± 0,7) ммоль/ дм³.
4.2.2. Числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и значение его погрешности (неопределенности).
Примеры
| Правильно | Неправильно |
| 0,043 ± 0,004 | 0,043 ± 0,0043 |
| 0,0428 ± 0,0043 | 0,0428 ± 0,004 |
| 17,0 ± 0,2 | 17,00 ± 0,2 или 17 ± 0,2 |
| 12,13 ± 0,17 или 12,1 ± 0,2 | 12,1 ± 0,17 или 12,13 ± 0,2 |
| 46,40 ± 4,64 или 46,4 ± 4,6 | 46,402 ± 4,64 или 46,4 ± 4,64 |
4.2.3. Значение погрешности (неопределенности) результата измерений представляют числом, содержащим одну или две значащих цифры. Если числовое значение погрешности (неопределенности) в целой части числа содержит три и более цифр, то результат и погрешность округляются до целых чисел без подсчета количества значащих цифр.
Примеры
| Результаты измерения |
| 0,14 ± 0,05 |
| 0,164 ± 0,051 |
| 1,1 ± 0,1 |
| 1,18 ± 0,11 |
| 3,6 ± 0,6 |
| 3,28 ± 0,54 |
| 12,4 ± 1,2 |
| 44 ± 4 |
| 44,2 ± 4,4 |
| 168 ± 34 |
| 2357 ± 212 |
| 23684 ± 1184 |
4.2.4. Если заказчик требует другие формы представления результатов измерений, лаборатория оставляет за собой право учитывать эти требования.
Ответственность за правильность обработки и представления результатов измерений несут специалисты лаборатории.
Представление результатов измерений на примере определения обобщенных и химических показателей в воде с учетом требований методик измерений
1. Железо общее (ГОСТ 4011-72)
Округлять результат до двух значащих цифр.
Примеры
| Окончательные результаты, мг/дм³ | Промежуточные результаты, мг/дм³ |
| 0,12 ± 0,03 | 0,116 ± 0,029 |
| 0,18 ± 0,04 | 0,178 ± 0,0445* |
| 0,18 ± 0,05 | 0,183 ± 0,046 |
| 0,31 ± 0,08 | 0,308 ± 0,077 |
| 1,3 ± 0,3 | 1,26 ± 0,32 |
| 1,8 ± 0,3 | 1,77 ± 0,32 |
| 12 ± 2 | 12,4 ± 2,2 |
| 25 ± 5 | 25,3 ± 4,6 |
2. Хлориды (ПНД Ф 14.1:2:3.96-97)
Численные значения результата измерений должны оканчиваться цифрой того же разряда, что и значения характеристики погрешности.
3. Фосфорсодержащие вещества (ГОСТ 18309-2014)
Числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и значение характеристики погрешности, выраженное в мг/дм³ и содержащее не более двух значащих цифр.
4. Взвешенные вещества (ПНД Ф 14.1:2:3.110-97)
Численные значения результата измерений должны оканчиваться цифрой того же разряда, что и значения характеристики погрешности.
5. Цветность (ГОСТ 31868-2012)
В протоколе указывают метод определения цветности по настоящему стандарту, результат с указанием единиц измерения (например, градусов цветности по хром-кобальтовой шкале Cr-Co) и температуру пробы анализируемой воды.
При определении цветности при постоянной комнатной температуре (20 ± 5) °С в конкретной лаборатории допускается по согласованию с заказчиком не указывать в протоколе значение температуры.
6. Металлы (ПНД Ф 14.1:2:4.139-98)
Примеры записи числовых значений:
| Диапазон, мг/дм³ | Точность округления, мг/дм³ |
| от 0,004 до 0,01 вкл. | 0,0001 |
| от 0,01 до 0,1 вкл. | 0,001 |
| от 0,1 до 1 вкл. | 0,01 |
| от 1 до 10 вкл. | 0,1 |
| свыше 10 | 1 |
7. Алюминий (ГОСТ 18165-2014)
Числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и абсолютное значение характеристики погрешности измерений, выраженное в мг/дм³. Абсолютное значение характеристики погрешности измерений представляют двумя значащими цифрами, если первая цифра не превышает 3. В остальных случаях оставляют одну значащую цифру.
Примеры
| Окончательные результаты, мг/дм³ | Промежуточные результаты, мг/дм³ |
| 0,287 ± 0,057 | 0,2872 ± 0,0574 |
| 0,262 ± 0,052 | 0,2623 ± 0,05246* |
| 2,38 ± 0,48 | 2,381 ± 0,476 |
| 13,5 ± 2,7 | 13,47 ± 2,69 |
| 16,6 ± 3,3 | 16,62 ± 3,32 |
| 22 ± 4 | 21,8 ± 4,4 |
| 27 ± 5 | 27,4 ± 5,48* |
| 38 ± 7 | 38,47* ± 7,7 |
| 51 ± 10 | 51,46* ± 10,3 |
8. Нефтепродукты (ПНД Ф 14.1:2:4.128-98)
Примеры записи числовых значений, мг/дм³:
| 0,009 ± 0,005 | 0,08 ± 0,03 |
| 0,65 ± 0,16 | 3,5 ± 0,9 |
| 3,5 ± 0,9 | 25 ± 6 |
9. Анионные поверхностно-активные вещества (ПНД Ф 14.1:2:4.158-2000)
| Примеры записи для питьевой воды, мг/дм³ | Примеры записи для природной и сточной воды, мг/дм³ |
| 0,028 ± 0,010 | 0,080 ± 0,032 |
| 0,44 ± 0,12 | 0,35 ± 0,11 |
| 4,8 ± 1,0 | 71 ± 17 |
10. Щелочность (МП УВК 1.19-2013)
Численные значения результата количественного химического анализа должны оканчиваться цифрой того же разряда, что и численное значение характеристики погрешности. Характеристику погрешности измерения следует выражать числом, содержащим не более двух значащих цифр.
11. Температура, прозрачность, запах (РД 52.24.496-2018)
Численное значение результата измерений должно оканчиваться цифрой того же разряда, что и значение характеристики погрешности.
12. Кальций (РД 52.24.403-2018)
Численные значения результата измерений должны оканчиваться цифрой того же разряда, что и значения погрешности; последние не должны содержать более двух значащих цифр.
13. Перманганатная окисляемость (ПНД Ф 14.1:2:4.154-99)
Результаты измерений округляют с точностью:
| Диапазон, мг/дм³ | Точность округления, мг/дм³ |
| от 0,25 до 1,0 вкл. | 0,01 |
| от 1,0 до 10 вкл. | 0,1 |
| свыше 10 | 1 |
14. Фториды (ПНД Ф 14.1:2:4.270-2012)
Результаты измерений концентрации фторид-ионов при занесении в протокол округляют с точностью:
| Диапазон, мг/дм³ | Точность округления, мг/дм³ |
| от 0,15 до 10 вкл. | 0,01 |
| свыше 10 | 0,1 |
15. Растворенный кислород (ПНД Ф 14.1:2:3.101-97)
Численные значения результата измерений должны оканчиваться цифрой того же разряда, что и значения характеристики погрешности.