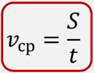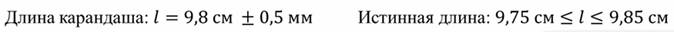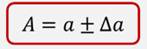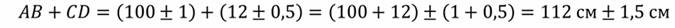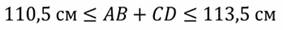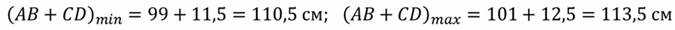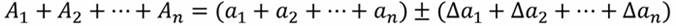Что такое погрешность в физике 7 класс определение кратко и понятно
Точность и погрешность измерений
Содержание
Одна из самых быстрых машин, которую можно встретить на городской дороге, — BMW M8 Competition, — согласно тестированиям автопроизводителя способна разгоняться до 100 км/ч за впечатляющие 2.5 с.
Иными словами, вы успеете моргнуть лишь единожды прежде, чем спидометр стильного немецкого купе выдаст отметку «100» и, озорно светя задними габаритными огнями, улетит в закат.
Рисунок 1: Панель приборов автомобиля. Спидометр располагается справа.
Физические величины различного рода и их измерения так или иначе окружают нас везде.
К примеру, та же вышеупомянутая динамика разгона, то есть время, за которое транспортное средство разгоняется до определенной скорости, является важным параметром для любого автомобилиста, приобретающего новенький спорткар в салоне.
В жару мы то и дело поглядываем на отметку термометра и ужасаемся, когда температура на отметке безжалостно приближается к 40 °C. Если опаздываем, то обязательно держим под рукой часы и проверяем время по минутам.
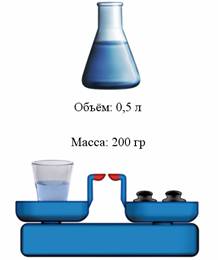
Если худеем, то каждое утро начинаем со взвешивания и фиксируем массу своего тела в килограммах. Если растем, то периодически интересуемся, сколько на этот раз метров и сантиметров покажет настенная линейка.
Правда несмотря на то, что физика относится к наукам точным, как бы удивительно ни было, ни одна ее величина — ни время, ни длина, ни скорость, ни что-либо еще — не может быть выражена с предельной точностью.
Ведь вряд ли вы весите, скажем, ровно 60 килограмм без единого лишнего миллиграмма или имеете рост ровно 170 сантиметров. Точно так же, как и BMW M8 Competition не разгоняется до 100 км/ч абсолютно ровно за две с половиной секунды.
Что такое точность?
Точность измерений характеризует близость результата измерения к фактическому значению измеряемой величины. Строго говоря, ни одна физическая величина не может быть измерена с абсолютной точностью — так, чтобы данные измерительного прибора отображали истинное значение.
Мир и его явления, на самом деле, практически всегда имеют отношение к иррациональным числам, таким, как, к примеру, результат деления десяти на три: наберите данную операцию на калькуляторе и посмотрите на то, как неэстетично в реальности выглядят данные — с кучей знаков после запятой, за которыми не угнаться.
Однако иррациональность чисел не удивляет, да и слишком абстрактна, дабы уловить суть. Что есть деление десяти на три? Тогда, для конкретности, стоит покуситься на святое — на время. Казалось бы, что может быть точнее времени, показываемого самыми точными на свете часами — атомными часами?
И тем не менее, даже если вы зайдете на онлайн-ресурс, официально регистрирующий международное атомное время с точностью до миллисекунд, действительного точного измерения времени там вы не найдете.
Всегда есть условности: задержка передачи данных между сетевыми элементами; ваш мозг, регистрирующий и обрабатывающий информацию, поступающую через органы чувств и т. д. Все это отдаляет нас, хоть и несущественно, от фактического значения величины.
Именно поэтому в физике одним из важнейших понятий является понятие погрешности.
Что такое погрешность?
Представьте, что вас отправили в магазин купить сахар, но вот незадача: фасованный в пачках как раз закончился и остался только на развес. Что делать, вы просите продавца тогда отмерить вам ровно килограмм. Продавец взял лопатку, наполнил пакет, положил его на весы, и они выдают значение — 1.000 кг.
Как удачно положили.
Вы рассчитываетесь и счастливым возвращаетесь домой. А теперь представим, что по необыкновенной случайности у вас дома имеются весы, показывающие массу с точностью до миллиграмма. Вы решаете интереса ради перевесить пакет, чтобы посмотреть, действительно ли его масса равна строго килограмму.
И какого же удивление, когда более точные весы показывают массу не в 1.000 кг, а в 0.999990 кг. Иными словами, вас обсчитали. Обсчитали, между прочим, на десять миллиграмм!
Чем меньше цена деления прибора, тем точнее измерение. Ваши весы с учетом массы до миллиграмма оказались точнее магазинных «граммовых» весов. Однако и это не предел, ведь существуют фармакологические весы, определяющие массу до микрограмма — одной миллиардной килограмма. Так можно продолжать до бесконечности, пока у нас не закончатся технологические возможности сконструировать еще более точные весы.
Однако все измерительные приборы, пусть и самые точные, несовершенны. Несовершенно даже само то, как мы видим, слышим и ощущаем мир вокруг. Это, наряду с прочими факторами, приводит к тому, что при измерении величины получается ее приближенное значение, не истинное.
Разница между приближенным и истинным значениями и называется погрешностью.
Важно. Погрешность не равно ошибке. В обычном, бытовом языке мы привыкли к тому, что слово «погрешность» у нас ассоциируется с просчетом или упущением.
В физике погрешность — обыденное явление, присутствующее внутри практически каждой величины, и мало что имеет общего с ошибкой в привычном понимании слова.
Все величины, которые, к примеру, вы видите в типовых физических задачах на вычисление, так или иначе содержат погрешность. Ее не обозначают для удобства. Поэтому помните о невозможности проводить эксперименты в идеальных условиях и о том, что ни один прибор чаще всего не сможет показать результат таким, каков он есть на самом деле.
Как правило, при однократном проведении измерения определить значение погрешности крайне затруднительно: для ее выявления обычно проводят серию равноточных измерений — измерений, произведенных в одинаковых условиях.
После результаты сличаются, то есть сравниваются между собой и, при необходимости, сопоставляются с различными экспериментальными величинами. На основе данных, полученных в результате измерений и сличения, вычисляется погрешность.
Эксперимент с линейкой
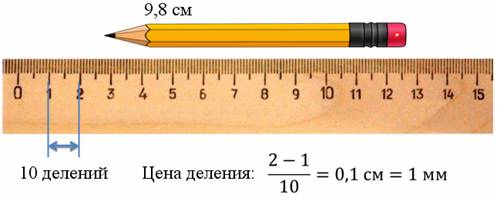
Обнаружить явление погрешности можно самостоятельно вне строгой лабораторной обстановки: достаточно провести простой эксперимент измерения длины с обычной школьной линейкой. В качестве примера, возьмем карандаш и выполним с ним замеры.
Рисунок 2. Замер линейкой с ценой деления 1 см.
Во-первых, необходимо зафиксировать цену деления измерительного прибора. Цена деления определяется разностью двух ближайших отметок. В нашем случае она равна 1 см.
Примечание. На разметке измерительного прибора всегда указываются единицы измерения. К примеру, на стандартной линейке можно увидеть пометку «см», сантиметры.
Довольно часто используемые для измерений приборы не работают с основными единицами СИ — единицы величин либо являются производными, как сантиметр, либо, как миллиметр ртутного столба, являются внесистемными.
Когда вас просят привести ответ в СИ, не забывайте о переводе значений, если измерительный прибор работает с внесистемными или производными единицами. В случае с сантиметровой линейкой, при подобном требовании, обязательно выражение результата в метрах и т. п.
Далее совмещаем конец карандаша с нулевой отметкой. Видим, что второй конец располагается между отметками 12 и 13.
Какой из этих результатов следует принять за длину нашего карандаша?
Очевидно, что тот, который будет ближе к истинному значению — 12 см. Если бы мы провели аналогичный опыт, использовав более точную линейку с ценой деления в миллиметр, мы получили бы значение 12.2 см.
Рисунок 3. Замер линейкой с ценой деления 1 мм.
А какой из этих результатов лучше будет засчитать теперь? Какой правильный?
Оба результата фактически являются верными, их разница заключается лишь в том, что получены они были с разной точностью измерения: длина карандаша во втором варианте была дана с точностью до миллиметра, в первом — до сантиметра. Можно было бы воспользоваться микро́метром, еще более точным измерительными прибором, и получить результат с точностью до микроме́тра. Однако в случае с карандашом точности до миллиметра будет достаточно.
Вычисление погрешности
Но что делать, если бы мы захотели учесть погрешность? Как ее вычислить и обозначить математически?
На самом деле, точно определить погрешность не так просто. Для этого необходимо владение методами математической статистики, для чего требуется уже знание высшей математики. Плюс немаловажно определение комплексных параметров вроде класса точности измерительного прибора.
Поэтому для простоты измерений с погрешностью считается, что обычно она равна половине цены деления прибора. В нашем эксперименте при цене деления линейки в сантиметр погрешность составила 0.5 см. При цене деления в миллиметр — 0.05 см.
$l$ = 12 ± 0.5 cм — в случае, когда цена деления составляла сантиметр;
$l$ = 12.2 ± 0.05 см — в случае, когда цена деления составляла миллиметр.
Математический символ плюс-минус (±) используется для обозначения интервала значений и расшифровывается следующим образом: истинное значение величины заключено в диапазоне «от-до».
Формула погрешности
Таким образом, общая формула для записи величин с погрешностью выглядит следующим образом:
Выходит, что истинное значение длины карандаша располагается в диапазоне значений от 11.5 см до 12.5 см.
При более точных замерах до миллиметра: от 12.15 см до 12.25 см.
Однако остается один последний интересный момент. Несмотря на то, что мы провели замеры и определили длину, философски говоря, вопрос остается вопросом: так какую же точную длину имеет карандаш?
Погрешности измерений, представление результатов эксперимента
п.1. Шкала измерительного прибора
Примеры шкал различных приборов:
 Манометр – прибор для измерения давления, круговая шкала |  Вольтметр – прибор для измерения напряжения, дуговая шкала |  Индикатор громкости звука, линейная шкала |
п.2. Цена деления
Пример определения цены деления:
 | Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале: a = 5 c b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. |
Цена деления: \begin Физическую величину измеряют с помощью прибора Измерение длины бруска линейкой Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений Определение площади столешницы при измеренной длине и ширине Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.) Определяется несовершенством методов и допущениями в методике. Погрешность теории (модели) Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности. Определяется субъективным фактором, ошибками экспериментатора. Примеры значащих цифр: В простейших измерениях инструментальная погрешность прибора является основной. Пример получения результатов прямых измерений с помощью линейки: Второе измерение точнее, т.к. его относительная погрешность меньше. Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки). Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений. Пример расчета истинного значения и погрешности для серии прямых измерений: Составим расчетную таблицу: Сначала находим среднее значение всех измерений: \begin Как найти результат прямого измерения, мы рассмотрели выше. Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса. Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно? Составим таблицу для расчета цены деления: Инструментальная точность мензурки равна половине цены деления. Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке. Ответ: Мерой точности является относительная погрешность измерений. Получаем: \begin Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч. Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины. При изучений физических явлений проводят различные измерения. При изучении падение тела, надо измерить высоту, с которой падает тело, массу тела, его скорость и время падения. Измерить какую-либо физическую величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины. Измерить длину стола — значит сравнить ее с другой длиной, которая принята за единицу длины, например с метром. 2. Какие бывают единицы имерения? Для каждой физической величины приняты свои единицы измерения. Очень удобно пользоваться одинаковыми единицами физических величин во всех странах мира. единица длины — 1 метр (1м), Кроме того, используются кратные единицы (кратные основной единице), которые в 10, 100, 1000 и т. д. раз больше. Используются и дольные единицы, которые в 10, 100, 1000 и т. д. раз меньше принятых единиц величин. Некоторые приставки к названиям единиц: г — гекто (100 или 10 2 ) 3. Что такое измерителный прибор? Для измерения физических величин нужны измерителные приборы. Есть измерителные приборы для простых измерений. Например, измерительная линейка, рулетка, мензурка, применяемая для измерения объема жидкости. У измерительных приборов есть измерительная шкала, на которой штрихами нанесены деления и написаны значения величин. Между двумя большими штрихами могут быть дополнительно нанесены несколько делений, не обозначенных числами. Значение измеряемой величины между ближайшими штрихами называется ценой деления прибора. Например, у обычной школьной линейки расстояние между двумя ближайшими штрихами составляет 1 мм, это цена деления линейки. 4. Как определить цену деления измерительной шкалы прибора? Прежде чем использовать измерительный прибор, надо определить цену деления этого прибора. Для того чтобы определить цену деления, необходимо: 5. Примеры определения цены деления а) Определение цены деления секундомера. Секундомер показывает 22 с. Любое измерение может быть выполнено с большей или меньшей точностью. Из этого примера видно, что точность измерений зависит от цены деления шкалы прибора. При записи величин, с учетом погрешности, пользуются формулой: где А — измеряемая величина, Если длина книги 20 см, а цена деления линейки 1 мм, то погрешность измерения будет равна 0,5 мм, или 0,05 см. Главное: Измерить какую-либо величину — это значит сравнить ее с однородной величиной, принятой за единицу этой величины. Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге. Физические величины. Точность и погрешность измерений Измерять – значит, познавать Данная тема посвящена физическим величина и их измерениям. В физике часто приходится измерять те или иные величины. Измерить можно высоту дома или длину улицы. Можно измерить объём воды в колбе или массу воды в стакане. Но что означают эти измерения? Измерить какую-либо величину – значит сравнить её с однородной величиной, принятой за единицу. Из приведённых выше примеров, можно заметить, что, например, единицей объёма является литр, а единицей массы является грамм. Для удобства была введена международная система единиц, которая называется СИ. Известно что, иногда применяются единицы измерения, которые в десятки, сотни, тысячи и так далее раз больше принятых единиц измерения. Такие единицы измерения называются кратными. У каждого ученика имеется линейка, длина которой измеряется в сантиметрах, то есть в единицах, которые в сто раз меньше метра. Поэтому, если длина линейки составляет 15 сантиметров, мы можем сказать, что её длина 0,15 метра. Линейка – это прибор для измерения длины. Конечно, линейка относится к самым простым измерительным приборам. Существуют значительно более сложные приборы: например, термометр, который применяется для измерения температуры, гигрометр, который используется для измерения влажности или амперметр, который используется для измерения силы электрического тока. Важно знать, как пользоваться измерительными приборами и насколько могут быть точны те или иные измерения. У каждого ученика есть линейка и карандаш. Можно попытаться измерить длину карандаша. В первую очередь нужно определить, какова цена деления измерительного прибора. Для этого необходимо найти два ближайших штриха шкалы, возле которых указаны значения величины (например, 1 см и 2 см). Далее нужно сосчитать число делений, заключенных между цифрами 1 и 2. При подсчёте получается, что количество этих делений равно 10. Таким образом, между отметками 1 см и 2 см заключено десять делений. Вычитаем из большего числа меньшее и делим на количество делений между ними. В результате вычислений получаем, что цена деления линейки составляет 0,1 см или 1 мм. Данный пример объясняет, как определить цену деления любого измерительного прибора. Как видно из рисунка, длина карандаша чуть меньше десяти сантиметров. Если бы на этой линейке не было миллиметровых делений, то можно было сказать, что длина карандаша равна десяти сантиметрам. Но это было бы не совсем точное измерение. Такую неточность называют погрешностью измерения. В представленном случае, на линейке есть миллиметровые деления, поэтому можно измерить длину карандаша с более высокой точностью – 9,8 см. Это говорит о том, что чем меньше цена деления, тем больше точность измерения. Ну а большая точность измерения означает меньшую погрешность. Однако абсолютно точных измерений не существует. Если дать один и тот же карандаш каждому ученику из класса и попросить измерить длину карандаша, не у всех получится одинаковый результат. Тем не менее, погрешность измерения не может быть больше цены деления. Например, если видно, что длина карандаша не точно 9,8 см, а чуточку больше, то понятно, что длина карандаша находится в промежутке от 9,8 см до 9,9 см. Погрешность измерений принято считать равной половине цены деления измерительного прибора. То есть, в рассмотренном случае, погрешность измерений составляет 0,5 мм. Поэтому, после того, как измерили карандаш и записали, что его длина равна 9,8 см, следует записать погрешность. Знак «±» означает, что указанная длина может быть на полмиллиметра больше или на полмиллиметра меньше. Таким образом, истинное значение длины карандаша находится в промежутке от 9,75 см до 9,85 см. В общем случае запись измеряемых величин с учетом погрешности имеет следующий вид: где А – измеряемая величина; а – результат измерения; Da – погрешность измерений. Необходимо отметить, что при сложении или вычитании величин с погрешностью, погрешность результата равна сумме погрешностей каждой величины. В этом легко убедиться на примере. На рисунке показаны два отрезка AB и CD, длины которых измерены с определенной погрешностью. Рассчитаем сумму длин этих отрезков. Из рисунка видно, что отрезок AB равен 1 м ± 1 см. Истинная длина этого отрезка находится в промежутке 99 см ≤ АВ ≤ 101 см. Отрезок CD равен 12 см ± 0,5 см. Истинная длина этого отрезка находится в промежутке от 11,5 см ≤ CD ≤ 12,5 см. Поэтому, сумма длин этих отрезков будет иметь еще большую погрешность. Прежде чем производить вычисления, необходимо перевести обе длины в одинаковые единицы измерения. Таким образом, получаем, что сумма длин отрезков AB и CD равна Важно отметить, что этот же промежуток мы бы получили, если бы сложили наименьшие и наибольшие длины отрезков AB и CD. Следовательно, при сложении или вычитании величин, измеренных с погрешностями, погрешность результата равна сумме погрешностей каждой из величин. Упражнение 1. Заполните таблицу, указав, что из перечисленных слов является физическим телом, единицей измерения, физической величиной или физическим явлением: ветер, Луна, килограмм, дерево, длина, скорость, испарение. Упражнение 2. Родители измерили рост братьев Димы и Васи с помощью рулетки, цена деления которой 1 см. Подсчитайте, насколько см Дима выше, чем Вася. Упражнение 3. Найдите суммарную массу животных с погрешностью. – Для описания физических тел или физических явлений вводится физическая величина, которую можно измерить с помощью измерительных приборов или вычислить по формуле. – Измерение величины – это сравнение её с однородной величиной, принятой за единицу. – Кратные приставки – это приставки означающие увеличение в десятки, сотни, тысячи и так далее раз. – Дольные приставки – это приставки, означающие уменьшение в десятки, сотни, тысячи и так далее раз. – Погрешность измерений – неточность допускаемая при измерении. За погрешность измерений данного прибора принимают половину цены деления этого прибора. – При сложении или вычитании величин с погрешностями, погрешность результата вычислений равна сумме погрешностей каждой величины.п.3. Виды измерений
п.4. Погрешность измерений, абсолютная и относительная погрешность
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:п.5. Абсолютная погрешность серии измерений
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.№ опыта 1 2 3 Сумма Масса, г 99,8 101,2 100,3 301,3 Абсолютное отклонение, г 0,6 0,8 0,1 1,5
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin
Поэтому абсолютная погрешность измерения массы: \begin п.6. Представление результатов эксперимента
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.п.7. Задачи
№ мензурки a, мл b, мл n \(\triangle=\frac 1 20 40 4 \(\frac<40-20><4+1>=4\) 2 100 200 4 \(\frac<200-100><4+1>=20\) 3 15 30 4 \(\frac<30-15><4+1>=3\) 4 200 400 4 \(\frac<400-200><4+1>=40\)
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):№ мензурки Объем \(V_0\), мл Абсолютная погрешность
\(\triangle V=\frac<\triangle><2>\), млОтносительная погрешность
\(\delta_V=\frac<\triangle V>1 68 2 3,0% 2 280 10 3,6% 3 27 1,5 5,6% 4 480 20 4,2%
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.Что такое погрешность в физике 7 класс определение кратко и понятно
Физики измеряют физические величины.
Чтобы узнать, например, зависит ли объем воды или другой жидкости от ее температуры и как зависит, нужно, нагревая воду, измерять и объем, и температуру.
Объем и температура, время и длина, площадь, скорость, масса, сила — это физические величины.
1. Что значит измерить?
В результате измерения величины получаем ее числовое значение, выраженное в принятых единицах.
Поэтому с 1963 г. применяется Международная система единиц — СИ (система интернациональная).
единица времени — 1 секунда (1с),
единица массы — 1 килограмм (1 кг).
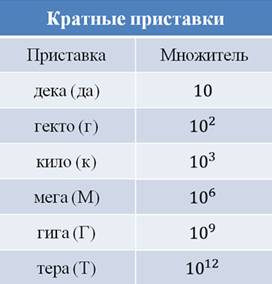
Эти единицы получили наименования с приставками, взятыми из греческого языка.
«Дека» — 10, «гекто» — 100, «кило» — 1000 и др.
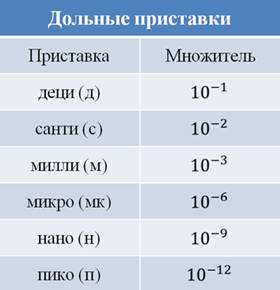
В них применяют приставки, также взятые из латинского языка. «Деци» — 0,1, «санти» — 0,01, «милли» — 0,001 и др.
к — кило (1000 или 10 3 )
М — мега (1 000 000 или 10 6 )
Есть сложные измерительные приборы: секундомеры, термометры и другие.
По мере развития физики и техники приборы усложнялись и появились, например, приборы, при помощи которых изучают строение вещества.
Надо установить, какому значению величины соответствует каждое самое малое деление.
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.
Используем любые два штриха, около которых нанесены значения измеряемой величины (времени), например штрихи с обозначениями 5 и 10 с.
Расстояние между этими штрихами разделено на 10 делений. Значит, цена каждого деления равна:
6. Что такое точность и погрешность измерений?
В физике допускаемую при измерении неточность называют погрешностью измерения.
Погрешность измерения не может быть больше цены деления измерительного прибора.
Чем меньше цена деления, тем больше точность измерения.
При измерении принято считать, что: погрешность измерений равна половине цены деления шкалы измерительного прибора.
а — результат измерений,
дельта а — погрешность измерений (треуголник — греч. буква «дельта»).
Следовательно, длину книги можно записать так:
L = (20 ±0,05) см,
где L — длина книги.
Истинное значение длины книги находится в интервале от 19,95 см до 20,05 см.
Основные единицы системы СИ: метр, килограмм, секунда.
Для того чтобы определить цену деления, необходимо:
— найти два ближайших штриха шкалы, возле которых написаны значения величины;
— вычесть из большего значения меньшее и полученное число разделить на число делений, находящихся между ними.Физические величины. Точность и погрешность измерений
Урок 2. Физика 7 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Получите невероятные возможности
Конспект урока «Физические величины. Точность и погрешность измерений»