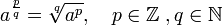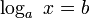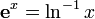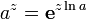Что такое показатель функции

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №21. Показательная функция.

Перечень вопросов, рассматриваемых в теме:

— какая функция называется показательной;

— какие свойства имеет показательная функция в зависимости от ее основания;

— какой вид имеет график показательной функции в зависимости от ее основания;

— примеры реальных процессов, описываемых показательной функцией.

Функция вида , a>0, а≠1 называется показательной функцией с основанием а.

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Определение, свойства и график показательной функции

Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.

Для положительного основания значение степени а х можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.

Сформулируем основные свойства показательной функции.

1. Область определения.

Как мы уже сказали, степень а х для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D_(y)=R.

2. Множество значений.

Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.

3. Корни (нули) функции.

Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.

При a>1 функция монотонно возрастает.

Рисунок 1 – График показательной функции при a>1

При 0 1 при х стремящемся к минус бесконечности.

2. Рассмотрим пример исследования функции y=–3 х +1.

1) Область определения функции – любое действительное число.

2) Найдем множество значений функции.

Так как 3 х >0, то –3 х х +1 х +1 представляет собой промежуток (-∞; 1).

3) Так как функция y=3 х монотонно возрастает, то функция y=–3 х монотонно убывает. Значит, и функция y=–3 х +1 также монотонно убывает.

4) Эта функция будет иметь корень: –3 х +1=0, 3 х =1, х=0.

Рисунок 3 – График функции y=–3 х +1

6) Для этой функции горизонтальной асимптотой будет прямая y=1.

3. Примеры процессов, которые описываются показательной функцией.

6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.

Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.

Рисунок 4 – График функции y=2 х – изменение количества информации

Примеры и разбор решения заданий тренировочного модуля

Выберите показательные функции, которые являются монотонно убывающими.

Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: , используя свойство степеней.

Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:

2) 4) 5)

Найдите множество значений функции y=3 x+1 – 3.

Так как 3 x+1 >0, то 3 x+1 – 3>–3, то есть множество значений:

Найдите множество значений функции y=|2 x – 2|

2 x –2>–2, но, так как мы рассматриваем модуль этого выражения, то получаем: |2 x – 2|0.

Источник

11.3.1. Показательная функция, ее свойства и график

Показательная функция — одна из основных функций, изучаемая в школе и в ВУЗе. Познакомимся с основными понятиями и свойствами показательной функции, построим ее график.

Справедливы все свойства степенной функции:

Примеры.

x=0, y=2 0 =1; Точка А.

x=1, y=2 1 =2; Точка В.

x=2, y=2 2 =4; Точка С.

x=3, y=2 3 =8; Точка D.

Большему значению аргумента х соответствует и большее значение функции у. Функция y=2 x возрастает на всей области определения D (y)=R, так как основание функции 2>1.

x=0, y=(½) 0 =1; Точка A.

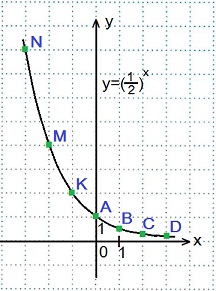
x=1, y=(½) 1 =½=0,5; Точка B.

x=2, y=(½) 2 =¼=0,25; Точка C.

x=3, y=(½) 3 =1/8=0,125; Точка D.

График функции у=2 х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.

Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R₊).

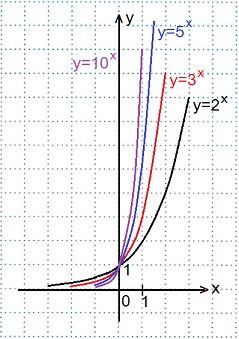
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.

4) В одной координатной плоскости построить графики функций:

Смотрите построение графика функции y=( 1 /₂) x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.

Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R₊.

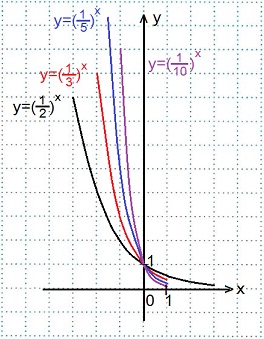
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.

Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.

Решить графически уравнения:

1) 3 x =4-x.

В одной координатной плоскости построим графики функций: у=3 х и у=4-х.

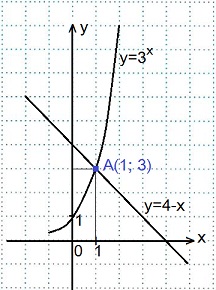
Графики пересеклись в точке А(1; 3).

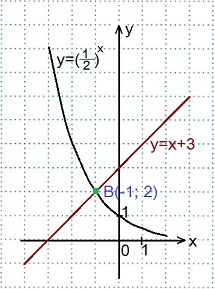
2) 0,5 х =х+3.

В одной координатной плоскости строим графики функций: у=0,5 х

Графики пересеклись в точке В(-1; 2).

1) y=-2 x

Область значений показательной функции y=2 x – все положительные числа, т.е.

0+ 1 1 /₃) x + 1 1 ;

Запишем функцию в виде: у=3 х ∙3-5.

0∙ 3 x ∙ 3 3 ;

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №21. Показательная функция.

Перечень вопросов, рассматриваемых в теме:

— какая функция называется показательной;

— какие свойства имеет показательная функция в зависимости от ее основания;

— какой вид имеет график показательной функции в зависимости от ее основания;

— примеры реальных процессов, описываемых показательной функцией.

Функция вида , a>0, а≠1 называется показательной функцией с основанием а.

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Определение, свойства и график показательной функции

Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.

Для положительного основания значение степени а х можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.

Сформулируем основные свойства показательной функции.

1. Область определения.

Как мы уже сказали, степень а х для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D_(y)=R.

2. Множество значений.

Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.

3. Корни (нули) функции.

Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.

При a>1 функция монотонно возрастает.

Рисунок 1 – График показательной функции при a>1

При 0 1 при х стремящемся к минус бесконечности.

2. Рассмотрим пример исследования функции y=–3 х +1.

1) Область определения функции – любое действительное число.

2) Найдем множество значений функции.

Так как 3 х >0, то –3 х х +1 х +1 представляет собой промежуток (-∞; 1).

3) Так как функция y=3 х монотонно возрастает, то функция y=–3 х монотонно убывает. Значит, и функция y=–3 х +1 также монотонно убывает.

4) Эта функция будет иметь корень: –3 х +1=0, 3 х =1, х=0.

Рисунок 3 – График функции y=–3 х +1

6) Для этой функции горизонтальной асимптотой будет прямая y=1.

3. Примеры процессов, которые описываются показательной функцией.

6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.

Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.

Рисунок 4 – График функции y=2 х – изменение количества информации

Примеры и разбор решения заданий тренировочного модуля

Выберите показательные функции, которые являются монотонно убывающими.

Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде: , используя свойство степеней.

Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:

2) 4) 5)

Найдите множество значений функции y=3 x+1 – 3.

Так как 3 x+1 >0, то 3 x+1 – 3>–3, то есть множество значений:

Найдите множество значений функции y=|2 x – 2|

2 x –2>–2, но, так как мы рассматриваем модуль этого выражения, то получаем: |2 x – 2|0.

Источник

Что такое показатель функции

График функции имеет следующий вид:

Рассмотрим свойства функции:

Примеры решения задач

Задача 1.

В одной координатной плоскости построить графики функций:

Решение.

x	-3	-2	-1	0	1	2	3
y(x)				1	2	4	8

Отметим полученные точки на координатной плоскости, соединив их плавной линией.

Большему значению аргумента х соответствует и большее значение функции у. Функция y = 2 x возрастает на всей области определения D(y)=R, так как основание функции 2 > 1.

Подобным образом построим графики остальных функций.

Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).

Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.

Задача 2.

В одной координатной плоскости построить графики функций:

Решение.

Для начала построим график функции . Для этого найдем значения функции при x = 0, ±1, ±2, ±3.

x	-3	-2	-1	0	1	2	3
y(x)	8	4	2	1

Отметим полученные точки на координатной плоскости, соединив их плавной линией.

Большему значению аргумента х соответствует меньшее значение функции y. Функция убывает на всей своей области определения: D(y)=R, так как основание функции 0

Подобным образом построим графики остальных функций.

Переменная х может принимать любое значение: D(y)=R, при этом область значений функции: E(y)=R+.

Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.

Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.

Задание 3.

Найти область значений функции:

Решение.

Область значений показательной функции y = 2 x – все положительные числа, т. е. 0 x x

2. y = +1

умножаем все части двойного неравенства на 3:

из всех частей двойного неравенства вычитаем 5:

Источник

Показатель степени

Число a b называется степенью с основанием a и показателем b.

Содержание

Натуральная степень

Число с называется n-ной степенью числа а, если .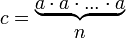

Существует алгоритм быстрого возведения в степень, выполняющий возведение в степень за меньшее, чем в определении, число умножений.

Целая степень

не определён

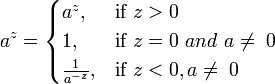
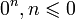
Рациональная степень

По определению,

Действительная степень

Пусть .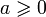

Другой подход основан на теории рядов и логарифмов. (см. определение комплексной степени)

Потенцирование

Потенцирование — это нахождение числа по известному значению его логарифма, то есть решение уравнения:

Комплексная степень

Определим некоторые функции:

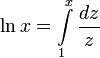
теперь для вычисления a z можно использовать свойства степеней и логарифмов:

Степень как функция

Поскольку в выражении x y принимает участие две переменных, то его можно рассматривать как:

См. также

Ссылки

Полезное

Смотреть что такое «Показатель степени» в других словарях:

Показатель степени — по техн. правилам набора должен набираться шрифтом, кегль которого в два раза меньше кегля шрифта символов и цифр, но без ущерба для удобочитаемости: Кегль символа или цифры Показатель степени 1 го порядка 2 го порядка 12 6 4 или 6 10 5 или 6 4… … Издательский словарь-справочник

показатель степени — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN power exponentsuperscript … Справочник технического переводчика

показатель степени — laipsnio rodiklis statusas T sritis fizika atitikmenys: angl. potenz vok. Exponent, m; Potenz, f rus. показатель степени, m pranc. exposant, m … Fizikos terminų žodynas

показатель степени — Syn: степень … Тезаурус русской деловой лексики

показатель степени сосредоточенности источников информации в сети — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN locality … Справочник технического переводчика

показатель степени числа — порядок числа — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы порядок числа EN number exponent … Справочник технического переводчика

показатель степени опасности компонента отхода — 3.1.9 показатель степени опасности компонента отхода: Интегральный показатель, характеризующий степень опасности компонента отхода при воздействии его на окружающую природную среду; Источник: СТО Газпром 12 2005: Каталог отходов производства и… … Словарь-справочник терминов нормативно-технической документации

ПОКАЗАТЕЛЬ СТЕПЕНИ СЖАТИЯ ГРУНТА — величина, характеризующая уменьшение объема породы по отношению к начальному объему осадки. Определяется по формуле где еf коэффициент пористости грунта при верхнем пределе пластичности; е коэффициент пористости при естественной влажности и… … Словарь по гидрогеологии и инженерной геологии

ЭКСПОНЕНТА, ПОКАЗАТЕЛЬ СТЕПЕНИ — (exponent) Одно из названий показателя степени; если у = хn, n является экспонентой. Экспонента не обязательно должна быть целым числом; если z – натуральный логарифм х, т. е., х = еz, мы получаем у = хn = (еz)n = ezn, значение которого может… … Экономический словарь

дробный показатель степени — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN fractional exponent … Справочник технического переводчика

Источник