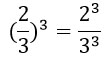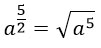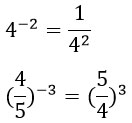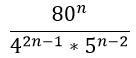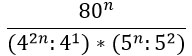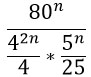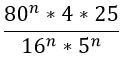Что такое показатель степени в алгебре

Свойства степеней. Действия со степенями

Что такое степень числа

В учебниках по математике можно встретить такое определение:

«Степенью n числа а является произведение множителей величиной а n раз подряд»

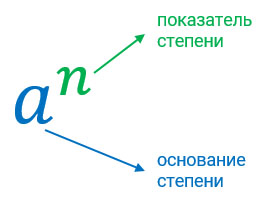
a — основание степени;

n — показатель степени.

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:

2 — основание степени;

3 — показатель степени.

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. За один год вы заработали на нем еще два. Еще через год каждый миллион принес еще два и т. д. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени 2) и куб (показатель степени 3).

Источник

Что такое степень числа

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

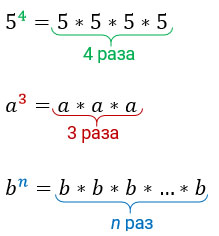
Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4 6

Выражение 4 6 называют степенью числа, где:

В общем виде степень с основанием « a » и показателем « n » записывается с помощью выражения:

Исключение составляют записи:

Конечно, выражения выше можно читать и по определению степени:

Степенью числа « а » с показателем n = 1 является само это число:
a 1 = a

Любое число в нулевой степени равно единице.
a 0 = 1

Ноль в любой натуральной степени равен нулю.
0 n = 0

Единица в любой степени равна 1.
1 n = 1

Выражение 0 0 (ноль в нулевой степени) считают лишённым смысла.

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Пример. Возвести в степень.

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Квадрат любого числа есть положительное число или нуль, то есть:

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.

В то время как найти « −5 4 » означает, что пример нужно решать в 2 действия:

Пример. Вычислить: −6 2 − (−1) 4

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.

Для облегчения решения примеров полезно знать и пользоваться таблицей степеней, которую вы можете бесплатно скачать на нашем сайте.

Для проверки своих результатов вы можете воспользоваться на нашем сайте калькулятором «Возведение в степень онлайн».

Источник

Степени и их свойства

Данная тема очень легкая, если выучить все свойства степеней. Они, кстати, достаточно просты для запоминания.

Перед тем, как перейти в свойствам степеней, разберемся, что такое степень.

Показатель степени показывает (масло масляное) сколько раз мы умножаем основание на себя. Это очень хорошо проглядывается на следующих примерах:

Вроде бы ничего сложного нет, правда?

Что ж, время перейти к свойствам.

Свойства степеней.

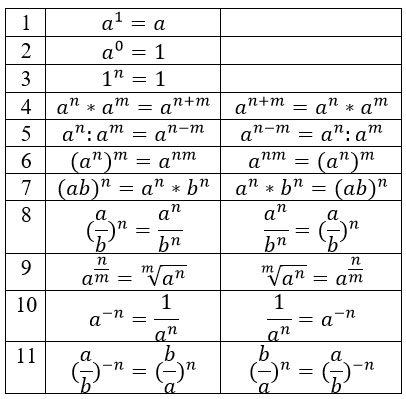
1. Любое число в первой степени равно самому себе: a 1 = a.

Сразу рассмотрим примеры.

2. Любое число в нулевой степени равно 1: а 0 = 1.

3. Единица в любой степени равна 1: 1 n = 1.

Это свойство легко доказать на числовом примере.

Конечно, так никто не расписывает, а сразу пользуется готовой формулой. Вот еще несколько примеров:

3 4 · 3 9 · 3 15 = 3 4 + 9 + 15 = 3 2 8 ;

Еще парочка примеров:

(2 2 ) 3 = 2 2 · 3 = 2 6 ;

8. Чтобы возвести дробь в степень надо и числитель, и знаменатель возвести в эту степень:.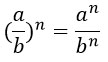

9. Степень с дробным показателем можно представить в виде корня некоторой степени по формуле 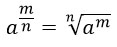(а > 0, n ≥ 2).

10. Чтобы возвести число, отличное от нуля, в степень с отрицательным показателем надо взять число, обратное данному, и возвести его в ту же степень, только без минуса: 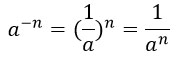(a ≠ 0).

Это же правило работает и для дробей: 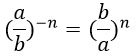(a ≠ 0, b ≠ 0).

Все эти свойства срабатывают как в одну сторону, так и в другую. Соберем их в аккуратную табличку.

Нам нужно сократить такую дробь:

Преобразуем знаменатель дроби, дважды использовав формулу по номером 5 из второго столбика таблицы.

Получившиеся частные в знаменателе запишем в виде дробей.

Получилась трехярусная дробь (можно произведение дробей в знаменателе переписать под одну черту). Нижний ярус этой дроби перейдет в верхний. Это не магия вне Хогвартса, но описывать эти преобразования текстом очень грустно. Если коротенько, то при делении на дробь мы ее переворачиваем и получается, что знаменатель заползает наверх 🙂

Переходим к финалу. Преобразуем знаменатель по свойству 7 из второго столбика таблицы (снова) и, наконец-таки, сокращаем дробь!

Источник

Алгебра. 7 класс

Конспект урока

Перечень вопросов, рассматриваемых в теме:

Понятие степени числа.

Степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.

Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований.

Произведение степеней с одним и тем же основанием – это степень с тем же основанием и показателем, равным сумме показателей этих степеней.

Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней.

1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.

1. Макарычев Ю. Н. Алгебра: 7 класс. // Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. – М.: Просвещение, 2019. – 256 с.

2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.

3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.

Теоретический материал для самостоятельного изучения.

Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

При этом число 8 называют основанием степени, а число 6 – показателем степени.

А теперь давайте сформулируем общее определение степени числа, опираясь на предыдущий пример:

степенью числа a с натуральным показателем n, бóльшим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.

Запись a n читается как: а в степени n, или n-ая степень числа a.

А вот следующие записи можно произносить по-разному:

a 2 – её можно произносить «а в квадрате» или «а во второй степени»;

a 3 – её можно произносить «а в кубе» или «а в третьей степени».

Стоит отметить, что особые случаи возникают, если показатель степени равен нулю или единице:

степенью числа а с показателем n = 1 является само это число:

любое число в нулевой степени равно единице:

ноль в любой натуральной степени равен нулю:

единица в любой степени равна 1:

Выражение 0 0 (ноль в нулевой степени) считают неопределенным.

Примеры. Возведём в степени:

При решении задач, нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Рассмотрим несколько примеров.

Возведём в степень

2 5 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 = 32

2,5 3 = 2,5 ∙ 2,5 ∙ 2,5 = 15,625

Основание степени может быть любым числом – положительным, отрицательным или нулём.
При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа, в результате может получиться как положительное число, так и отрицательное число. Это зависит от того, чётным или нечётным числом был показатель степени.

(-5) 4 = (-5) ∙ (-5) ∙ (-5) ∙ (-5) = 625.

Рассмотрим такой пример: 4 2 ∙ 5 2 = 4 ∙ 4 ∙ 5 ∙ 5 = (4 ∙ 5) ∙ (4 ∙ 5) = (4 ∙ 5) 2 = 20 2 = 400.

Данный пример подтверждает справедливость следующего свойства степеней:

Произведение степеней с одним и тем же показателем равно степени с тем же показателем и основанием, равным произведению оснований:

Этот пример подтверждает справедливость следующего свойства степеней:

Произведение степеней с одним и тем же основанием это степень с тем же основанием и показателем, равным сумме показателей этих степеней, т.е.

Наконец, рассмотрим равенство:

Это равенство подтверждает справедливость следующего свойства степеней:

Степень степени числа равна степени того же числа с показателем, равным произведению показателей этих степеней, т.е.

Разбор решения заданий тренировочного модуля

№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Источник

Степень числа: определения, обозначение, примеры

В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.

Степени с натуральными показателями: понятие квадрата и куба числа

Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).

Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.

Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.

Что такое степени с целым показателем

В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.

Степень числа с целым положительным показателем можно отобразить в виде формулы: .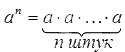

При этом n – любое целое положительное число.

Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:

Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0

При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.

Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).

Проиллюстрируем нашу мысль конкретными примерами:

В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:

Что такое степени с рациональным показателем

Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.

Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.

Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.

Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как

При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.

Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.

Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.

Объединим все данные выше определения в одной записи:

Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.

Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.

При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:

Что такое степени с иррациональным и действительным показателем

Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.

и так далее (при этом сами приближения являются рациональными числами).

Источник