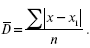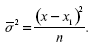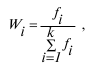Что такое показатели вариации в статистике

ЛЕКЦИЯ № 8. Показатели вариации

ЛЕКЦИЯ № 8. Показатели вариации

1. Понятие вариации

Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по–разному сочетаются в каждом отдельном случае.

Колебания отдельных значений характеризуют показатели вариации.

Термин «вариация» произошел от лат. variatio – «изменение, колеблемость, различие». Под вариацией понимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую.

Систематическая вариация помогает оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов.

Абсолютные и средние показатели вариации и способы их расчета

Для характеристики колеблемости признака используется ряд показателей, такие как размах вариации, определяемый как разность между наибольшим (х мах ) и наименьшим (х т щ) значениями вариантов:

Среднее линейное отклонение исчисляют для того, чтобы дать обобщающую характеристику распределению отклонений, которое учитывает различия всех единиц изучаемой статистической совокупности. Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней без учета знака этих отклонений:

На практике меру вариации более объективно отражает показатель дисперсии ( 2 – средний квадрат отклонений), определяемый как средняя из отклонений, возведенных в квадрат (х – х 1) 2 :

Среднее квадратическое отклонение – это мерило надежности средней.

Свойства дисперсии (доказываемые в математической статистике), которые позволяют упростить расчеты:

2) если все значения вариант разделить на какое–то постоянное число А, то средний квадрат отклонений уменьшится от этого в А 2 раз, а среднее квадратическое отклонение – в А раз

Показатели относительного рассеивания

Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах, которые позволяют сравнивать характер рассеивания в различных распределениях. Расчет показателей меры относительного рассеивания осуществляют отношением абсолютного показателя рассеивания к средней арифметической и умножают на 100%. Виды дисперсий и закон сложения дисперсий При помощи группировок, подразделив изучаемую совокупность на группы, однородные по признаку–фактору, можно определить три показателя колеблемости признака в совокупности: общую дисперсию, межгрупповую дисперсию и среднюю из внут–ригрупповых дисперсий.

Общая дисперсия характеризует вариацию признака, зависящую от всех условий в изучаемой статистической совокупности. Исчисляется общая дисперсия по формуле:

где х 0 – общая средняя для всей изучаемой совокупности.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

Вариации на тему

Вариации на тему У невероятных сделок и фантастических возможностей есть лишь одна проблема: они слишком часто кажутся заслуживающими внимания и доверия.Способность создавать иллюзии присуща любому успешному продавцу. Один успешный и совершенно честный трейдер,

26. Показатели вариации

26. Показатели вариации Вариационными называют ряды распределени построенные по количественному признаку. Значени количественных признаков у отдельных единиц сов купности непостоянны, более или менее различают между собой. Такое различие в величине признака н сит

ЛЕКЦИЯ № 2. Макроэкономические показатели

ЛЕКЦИЯ № 2. Макроэкономические показатели 1. Система национальных счетов Впервые термин «национальное счетоводство» был принят голландским ученым Ван Клиффом в 1950 г. Предпосылками развития системы национального счетоводства (СНС) послужили великая экономическая

ЛЕКЦИЯ № 5. Показатели развития национальной экономики и социально-трудовые отношения

ЛЕКЦИЯ № 5. Показатели развития национальной экономики и социально-трудовые отношения 1. Понятие экономического роста и развития национальной экономики Ведущим экономическим показателем является экономический рост, так как он отражает способность национальной

ЛЕКЦИЯ № 4. Статистические величины и показатели

ЛЕКЦИЯ № 4. Статистические величины и показатели 1. Назначение и виды статистических показателей и величин Природа и содержание статистических показателей соответствуют тем экономическим и социальным явлениям и процессам, которые их отражают. Все экономические и

ЛЕКЦИЯ №5. Средние величины и показатели вариации

ЛЕКЦИЯ №5. Средние величины и показатели вариации 1. Средние величины и общие принципы их исчисления Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на

3. Показатели вариации

3. Показатели вариации Целью статистического исследования является выявление основных свойств и закономерностей изучаемой статистической совокупности. В процессе сводной обработки данных статистического наблюдения строят ряды распределения. Различают два типа рядов

32. Понятие вариации

32. Понятие вариации Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов

Как построить правильную систему показателей: результирующие показатели и показатели‑факторы

Как построить правильную систему показателей: результирующие показатели и показатели?факторы Если вы до сих пор внимательно читали книгу, то, возможно, скажете: «Понятно, в чем главная ошибка этих грешников: они просто не измеряют эффективность своих процессов». И вы

Вопрос 58. Показатели равномерности и ритмичности поставок продукции. Показатели статистики перевозок грузов

Вопрос 58. Показатели равномерности и ритмичности поставок продукции. Показатели статистики перевозок грузов Равномерностью называется соблюдение сроков и размеров поставки, оговоренных контрактом.Оценку степени равномерности поставок можно получить с помощью

ЛЕКЦИЯ № 6. Обобщающие статистические показатели

ЛЕКЦИЯ № 6. Обобщающие статистические показатели 1. Виды и значение обобщающих показателей Обобщающие статистические показатели отражают количественную сторону изучаемой совокупности общественных явлений. Они представляют собой статистическую величину, выраженную

1. Понятие вариации

1. Понятие вариации Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов

Приложение Вариации на тему (играем несколько ролей, но не все сразу!)

Приложение Вариации на тему (играем несколько ролей, но не все сразу!) Далеко не всегда, описывая менеджера или команду в системе кодировки PAEI, мы можем использовать заглавные буквы. Выдающийся продавец может оказаться Р; посредственный продавец, имеющий некоторые

Вариации на тему

Источник

3. Показатели вариации

3. Показатели вариации

Целью статистического исследования является выявление основных свойств и закономерностей изучаемой статистической совокупности. В процессе сводной обработки данных статистического наблюдения строят ряды распределения. Различают два типа рядов распределения – атрибутивные и вариационные – в зависимости от того, является ли признак, взятый за основу группировки, качественным или количественным.

Вариационными называют ряды распределения, построенные по количественному признаку. Значения количественных признаков у отдельных единиц совокупности непостоянны, более или менее различаются между собой. Такое различие в величине признака носит название вариации. Отдельные числовые значения признака, встречающиеся в изучаемой совокупности, называют вариантами значений. Наличие вариации у отдельных единиц совокупности обусловлено влиянием большого числа факторов на формирование уровня признака. Изучение характера и степени вариации признаков у отдельных единиц совокупности является важнейшим вопросом всякого статистического исследования. Для описания меры изменчивости признаков используют показатели вариации.

Другой важной задачей статистического исследования является определение роли отдельных факторов или их групп в вариации тех или иных признаков совокупности. Для решения такой задачи в статистике применяются специальные методы исследования вариации, основанные на использовании системы показателей, с помощью которых измеряется вариация. В практике исследователь сталкивается с достаточно большим количеством вариантов значений признака, что не дает представления о распределении единиц по величине признака в совокупности. Для этого проводят расположение всех вариантов значений признака в возрастающем или убывающем порядке. Этот процесс называют ранжированием ряда. Ранжированный ряд сразу дает общее представление о значениях, которые принимает признак в совокупности.

Недостаточность средней величины для исчерпывающей характеристики совокупности заставляет дополнять средние величины показателями, позволяющими оценить типичность этих средних путем измерения колеблемости (вариации) изучаемого признака. Использование этих показателей вариации дает возможность сделать статистический анализ более полным и содержательным и тем самым глубже понять сущность изучаемых общественных явлений.

Самыми простыми признаками вариации являются минимум и максимум – это наименьшее и наибольшее значение признака в совокупности. Число повторений отдельных вариантов значений признаков называют частотой повторения.

Частость – относительный показатель частоты, который может быть выражен в долях единицы или процентах, позволяет сопоставлять вариационные ряды с различным числом наблюдений. Формально имеем:

где f i – число вариантов.

Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся среднее линейное отклонение, размах вариации, дисперсия, среднее квадратическое отклонение.

Размах вариации (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности, формально имеем:

Этот показатель дает лишь самое общее представление о колеблемости изучаемого признака, ибо показывает разницу только между предельными значениями вариантов. Он совершенно не связан с частотами в вариационном ряду, т. е. с характером распределения, а его зависимость только от крайних значений признака может придавать ему неустойчивый, случайный характер. Размах вариации не дает никакой информации об особенностях исследуемых совокупностей и не позволяет оценить степень типичности полученных средних. Область применения этого показателя ограничена достаточно однородными совокупностями. Точнее характеризует вариацию признака показатель, основанный на учете изменчивости всех значений признака.

Для характеристики вариации признака нужно уметь обобщить отклонения всех этих значений от какой-либо типичной для изучаемой совокупности величины. Такие показатели вариации, как среднее линейное отклонение, дисперсия и среднее квадра-тическое отклонение, основаны на рассмотрении отклонений значений признака отдельных единиц совокупности от средней арифметической.

Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической:

где d– среднее линейное отклонение;

Первая формула применяется, если каждый из вариантов встречается в совокупности только один раз, а вторая – в рядах с неравными частотами.

Существует и другой способ усреднения отклонений вариантов от средней арифметической. Этот очень распространенный в статистике способ сводится к расчету квадратов отклонений вариантов от средней с их последующим усреднением. При этом мы получаем новый показатель вариации – дисперсию.

Дисперсия (? 2 ) – средняя из квадратов отклонений вариантов значений признака от их средней величины:

Вторая формула применяется при наличии у вариантов своих весов (или частот вариационного ряда).

В экономико-статистическом анализе вариацию признака принято оценивать чаще всего с помощью среднего квадратического отклонения. Среднее квадратическое отклонение (?) представляет собой корень квадратный из дисперсии:

Среднее линейное и среднее квадратическое отклонения показывают, на сколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражаются в тех же единицах измерения, что и варианты.

В статистической практике часто возникает необходимость сравнения вариации различных признаков. Например, большой интерес представляет сравнение вариаций возраста персонала и его квалификации, стажа работы и размера заработной платы и т. д. Для подобных сопоставлений показатели абсолютной колеблемости признаков (среднее линейное и среднее квадртиче-ское отклонение), конечно, непригодны. Нельзя, в самом деле, сравнивать колеблемость стажа работы, выражаемую в годах, с колеблемостью заработной платы, выражаемой в рублях и копейках.

При сравнении изменчивости различных признаков в совокупности удобно применять относительные показатели вариации. Эти показатели вычисляются как отношение абсолютных показателей к средней арифметической (или медиане). Используя в качестве абсолютного показателя вариации размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, получают относительные показатели колеблемости:

Коэффициент вариации – наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% для распределений, близких к нормальному.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

Вариации на тему

Вариации на тему У невероятных сделок и фантастических возможностей есть лишь одна проблема: они слишком часто кажутся заслуживающими внимания и доверия.Способность создавать иллюзии присуща любому успешному продавцу. Один успешный и совершенно честный трейдер,

Показатели

Показатели Эффективность – показатель выпуска товаров и услуг (результата) в расчете на единицу затрат.Дисконтированный денежный поток – будущая стоимость ожидаемых денежных поступлений и выплат на конкретную дату.Срок окупаемости – период полного возврата

26. Показатели вариации

26. Показатели вариации Вариационными называют ряды распределени построенные по количественному признаку. Значени количественных признаков у отдельных единиц сов купности непостоянны, более или менее различают между собой. Такое различие в величине признака н сит

ЛЕКЦИЯ №5. Средние величины и показатели вариации

ЛЕКЦИЯ №5. Средние величины и показатели вариации 1. Средние величины и общие принципы их исчисления Средние величины относятся к обобщающим статистическим показателям, которые дают сводную (итоговую) характеристику массовых общественных явлений, так как строятся на

32. Понятие вариации

32. Понятие вариации Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов

Как построить правильную систему показателей: результирующие показатели и показатели‑факторы

Как построить правильную систему показателей: результирующие показатели и показатели?факторы Если вы до сих пор внимательно читали книгу, то, возможно, скажете: «Понятно, в чем главная ошибка этих грешников: они просто не измеряют эффективность своих процессов». И вы

Вопрос 58. Показатели равномерности и ритмичности поставок продукции. Показатели статистики перевозок грузов

Вопрос 58. Показатели равномерности и ритмичности поставок продукции. Показатели статистики перевозок грузов Равномерностью называется соблюдение сроков и размеров поставки, оговоренных контрактом.Оценку степени равномерности поставок можно получить с помощью

Вопрос 92. Обобщающие показатели уровня жизни населения. Показатели обеспеченности жильем населения и качества жилья

Вопрос 92. Обобщающие показатели уровня жизни населения. Показатели обеспеченности жильем населения и качества жилья Основным обобщающим показателем уровня жизни населения является индекс развития человеческого потенциала (ИРЧП). Данный индекс является составным,

ЛЕКЦИЯ № 8. Показатели вариации

ЛЕКЦИЯ № 8. Показатели вариации 1. Понятие вариации Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным

1. Понятие вариации

1. Понятие вариации Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов

Приложение Вариации на тему (играем несколько ролей, но не все сразу!)

Приложение Вариации на тему (играем несколько ролей, но не все сразу!) Далеко не всегда, описывая менеджера или команду в системе кодировки PAEI, мы можем использовать заглавные буквы. Выдающийся продавец может оказаться Р; посредственный продавец, имеющий некоторые

Показатели

Показатели Выполнение чрезвычайного плана затронуло все структуры Caterpillar и изменило сам способ ведения бизнеса в компании. Среди наиболее заметных корректировок, внесенных CAT в свою деятельность, были следующие:• Уровень занятости в целом по компании на конец года упал

Вариации на тему

Источник

Показатели вариации

Поможем написать любую работу на аналогичную тему

Показатели вариации. При изучении варьирующего признака у единиц совокупности нельзя ограничиваться лишь расчетом средней величины из отдельных вариантов, так как одна и та же средняя может относиться далеко не к одинаковым по составу совокупностям.

Вариацией признака называется различие индивидуальных значений признака внутри изучаемой совокупности.

Термин «вариация» произошел от латинского variatio – изменение, колеблемость, различие. Однако не всякие различия принято называть вариацией.

Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Колеблемость отдельных значений характеризуют показатели вариации. Чем больше вариация, тем дальше в среднем отдельные значения лежат друг от друга.

Различают вариацию признака в абсолютных и относительных величинах.

К абсолютным показателям относятся: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсия. Все абсолютные показатели имеют ту же размерность, что и изучаемые величины.

К относительным показателям относятся коэффициенты осцилляции, линейного отклонения и вариации.

Показатели абсолютные. Рассчитаем абсолютные показатели, характеризующие вариацию признака.

Размах вариации, представляет собой разность между максимальным и минимальным значением признака.

Показатель размаха вариации не всегда применим, так как он учитывает только крайние значения признака, которые могут сильно отличаться от всех других единиц.

Более точно можно определить вариацию в ряду при помощи показателей, учитывающих отклонения всех вариантов от средней арифметической.

Таких показателей в статистике два: среднее линейное и среднее квадратическое отклонение.

Среднее линейное отклонение (L) представляет собой среднее арифметическое из абсолютных значений отклонений отдельных вариантов от средней.

– для несгруппированных данных;

– для сгруппированных данных.

Практическое использование среднего линейного отклонения заключается в следующем, с помощью этого показателя анализируется состав работающих, ритмичность производства, равномерность поставок материалов.

Недостаток этого показателя заключается в том, что он усложняет расчеты вероятного типа, затрудняет применение методов математической статистики.

Среднее квадратическое отклонение () является наиболее распространенным и общепринятым показателем вариации. Оно несколько больше среднего линейного отклонения. Для умеренно асимметричных распределений установлено следующее соотношение между ними

=1,25L

Для его исчисления каждое отклонение от средней возводится в квадрат, все квадраты суммируются (с учетом весом), после чего сумма квадратов делится на число членов ряда и из частного извлекается корень квадратный.

Все эти действия выражает следующая формула

– для несгруппированных данных,

– для сгруппированных данных.

т.е. среднее квадратическое отклонение представляет собой корень квадратный из средней арифметической квадратов отклонений от средней.

Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше σ, тем лучше среднее арифметическое отражает собой всю представляемую совокупность.

Средняя арифметическая из квадратов отклонений вариантов значений признака от средней величины носит название дисперсии (), которая рассчитывается по формулам

– для несгруппированных,

– для сгруппированных.

Отличительной особенностью данного показатели является то, что при возведении в квадрат () удельный вес малых отклонений уменьшается, а больших увеличивается в общей сумме отклонений.

Дисперсия обладает рядом свойств, некоторые из них позволяют упростить её вычисление:

1. Дисперсия постоянной величины равна 0.

Если , то и .

Тогда .

2. Если все варианты значений признака (x) уменьшить на одно и то же число, то дисперсия не уменьшится.

Пусть , но тогда в соответствии со свойствами средней арифметической и .

Дисперсия в новом ряду будет равна

, т.е. дисперсия в ряду равна дисперсии первоначального ряда .

3. Если все варианты значений признака уменьшить в одно и то же число раз (k раз), то дисперсия уменьшится в k2 раз.

Пусть , тогда и .

Дисперсия же нового ряда будет равна

Выше был рассмотрен расчет показателей вариации для количественных признаков, но в экономических расчетах может ставиться задача оценки вариации качественных признаков. Например, при изучении качества изготовленной продукции, продукцию можно разделить на качественную и бракованную.

В таком случае речь идет об альтернативных признаках.

Альтернативными признаками называются такие, которыми одни единицы совокупности обладают, а другие нет. Например, наличие производственного стажа у абитуриентов, ученая степень у преподавателей ВУЗов и т.д. Наличие признака у единиц совокупности условно обозначаем через 1, а отсутствие – 0. Тогда, если долю единиц, обладающих признаком (в общей численности единиц совокупности), обозначить через р, а долю единиц, не обладающих признаком, через q, дисперсию альтернативного признака можно рассчитать по общему правилу. При этом p + q = 1 и, значит, q = 1– p.

Сначала рассчитываем среднее значение альтернативного признака:

Рассчитаем среднее значение альтернативного признака

,

т.е. среднее значение альтернативного признака равно доле единиц, обладающих данным признаком.

Дисперсия же альтернативного признака будет равна:

Таким образом, дисперсия альтернативного признака равняется произведению доли единиц, обладающих данным признаком, на долю единиц, не обладающих данным признаком.

А среднее квадратическое отклонение будет равно =.

Показатели относительные. Для целей сравнения колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях представляют интерес показатели вариации, выраженные в относительных величинах. Базой для сравнения служит средняя арифметическая. Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане.

Чаще всего они выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%. Различают следующие относительные показатели вариации:

1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней.

.

2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отношений от средней величины.

.

3. Коэффициент вариации оценивает типичность средних величин.

.

Чем меньше , тем однороднее совокупность по изучаемому признаку и типичнее средняя. Если ≤33%, то распределение близко к нормальному, а совокупность считается однородной. Из приведенного примера вторая совокупность однородна.

Виды дисперсий и правило сложения дисперсий. Наряду с изучением вариации признака по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.

При этом можно определить три показателя колеблемости признака в совокупности:

1. Общую вариацию совокупности, которая является результатом действия всех причин. Эта вариация может быть измерена общей дисперсией (), характеризующей отклонения индивидуальных значений признака совокупности от общей средней

.

2. Вариацию групповых средних, выражающих отклонения групповых средних от общей средней и отражающих влияние того фактора, по которому произведена группировка. Эта вариация может быть измерена так называемой межгрупповой дисперсией (δ2)

,

где — групповые средние, а -общая средняя для всей совокупности, и — численность отдельных групп.

3. Остаточную (или внутригрупповую) вариацию, которая выражается в отклонении отдельных значений признака в каждой группе от их групповой средней и, следовательно, отражает влияние всех прочих факторов кроме положенного в основу группировки. Поскольку вариацию в каждой группе отражает групповая дисперсия

,

то для всей совокупности остаточную вариацию будет отражать средняя из групповых дисперсий. Эту дисперсию называют средней из внутригрупповых дисперсий () и рассчитывается она по формуле

.

Общая вариация признака в совокупности должна определяться как сумма вариации групповых средних (за счет одного выделенного фактора) и остаточной вариации (за счет остальных факторов). Это равенство находит свое выражение в сложении дисперсий

.

Это равенство, имеющее строго математическое доказательство, известно, как правило сложения дисперсий.

Правило сложения дисперсий позволяет находить общую дисперсию по её компонентам, когда индивидуальные значения признака неизвестны, а в распоряжении имеются только групповые показатели.

Коэффициент детерминации. Правило сложения дисперсии позволяет выявить зависимость результатов от определенных факторов при помощи коэффициента детерминации.

,

Этот коэффициент показывает долю (удельный вес) общей вариации изучаемого признака, обусловленную вариацией группировочного признака.

Корень квадратный из коэффициента детерминации носит название корреляционного отношения ():

Оно характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака. Корреляционное отношение изменяется в пределах от 0 до 1. Если , то группировочный признак не оказывает влияния на результативный. Если , то результативный признак изменяется только в зависимости от признака, положенного в основание группировки, а влияние прочих факторных признаков равно нулю.

Показатели асимметрии и эксцесса. В области экономических явлений строго симметричные ряды встречаются крайне редко, чаще приходится иметь дело с асимметричными рядами.

В статистике для характеристики асимметрии пользуются несколькими показателями. Если учесть, что в симметричном ряду средняя арифметическая совпадает по значению с модой и медианой, то наиболее простым показателем асимметрии () будет разность между средней арифметической и модой, т.е. =.

Если ()>0, то на графике такой ряд будет иметь вытянутость вправо (правосторонняя асимметрия).

Если () 0, то эксцесс считают положительным (распределение островершинно), если

Источник