Что такое показательные неравенства
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №23. Показательные неравенства.
Перечень вопросов, рассматриваемых в теме
Показательным называется неравенство, в котором переменная входит только в показатели степеней, при постоянном основании.
Неравенства вида 
, 
называются простейшими показательными неравенствами.
Метод рационализации для решения показательных неравенств – переход от неравенства, содержащего показательные выражения, к равносильному рациональному неравенству (или равносильной системе рациональных неравенств).
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс. 216—220, 223-230.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
1. Рассмотрим показательные неравенства.
Показательным называется неравенство, в котором переменная входит только в показатели степеней, при постоянном основании.
Неравенства вида 
, 
называются простейшими показательными неравенствами.
Множество решения неравенства будет зависеть и от знака неравенства, и от основания степени, и от значения b.
Так как множество значений показательной функции 
– множество положительных чисел, то при 
неравенства: 
и 
решений не имеют, независимо от значения основания а. В то же время множеством решения неравенств 
и 
является все множество действительных чисел, независимо от значения основания а (см. Рисунок 1).
Рисунок 1 – иллюстрация решения простейшего показательного неравенства при b 0, a>1.
В том случае, когда основание степени a>1, то при переходе от исходного неравенства к неравенству с показателями знак неравенства не изменяется (см. Рисунки 2 и 3).
Рисунок 2 – иллюстрация решения простейшего показательного неравенства 
или 
при b>0, a>1.
Рисунок 3 – иллюстрация решения простейшего показательного неравенства 
или 
при b>0, a>1.
Теперь рассмотрим случай b>0, 0
В том случае, когда основание степени 0
Рисунок 4 – иллюстрация решения простейшего показательного неравенства 
или 
при b>0, 0 0, 0 3/7.
Рассмотрим еще один пример: 
.
Перепишем его в виде
.
Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменяется на противоположный:
,
,
.
Ответ: 
.
2. Теперь перейдем к решению более сложных показательных неравенств.
2.1) Рассмотрим пример: 
.
Преобразуем показатель первого слагаемого: 
.
Теперь в левой части вынесем за скобку общий множитель: 
.
Разделим обе части неравенства на 4: 
. Получили простейшее показательное неравенство. Так как основание степени больше 1, то при переходе к показателям знак неравенства сохраняется, получаем: 
. Решение этого неравенства является полуинтервал (0; 1].
2.2) Рассмотрим еще один пример: 
.
Заметим, что 
, поэтому введем новую переменную 
. Получим вспомогательное неравенство: 
.
.
Вернемся к исходной переменной:
, 
.
Так как основание степени меньше 1, то при переходе к показателям знак неравенства изменится на противоположный:
.
Ответ: 
.
2.3) Рассмотрим еще одной показательное неравенство, которое решается методом замены переменной.
.
Видим, что неравенство зависит от выражения 
, поэтому введем новую переменную 
и запишем вспомогательное неравенство: 
.
Решение показательных неравенств: основные способы
Многие считают, что показательные неравенства — это что-то такое сложное и непостижимое. И что научиться их решать — чуть ли не великое искусство, постичь которое способны лишь Избранные.
Полная брехня! Показательные неравенства — это просто. И решаются они всегда просто. Ну, почти всегда.:)
Сегодня мы разберём эту тему вдоль и поперёк. Этот урок будет очень полезен тем, кто только начинает разбираться в данном разделе школьной математики. Начнём с простых задач и будем двигаться к более сложным вопросам. Никакой жести сегодня не будет, но того, что вы сейчас прочитаете, будет достаточно, чтобы решить большинство неравенств на всяких контрольных и самостоятельных работах. И на этом вашем ЕГЭ тоже.
Как всегда, начнём с определения. — это любое неравенство, содержащее в себе показательную функцию. Другими словами, его всегда можно свести к неравенству вида
Конечно, в некоторых случаях неравенство может выглядеть более сурово. Вот, например:
Решение простейших показательных неравенств
Рассмотрим что-нибудь совсем простое. Например, вот это:
Как видим, чем большее число стоит в показателе степени, тем больше получается число на выходе. «Спасибо, кэп!» — воскликнет кто-нибудь из учеников. Разве бывает по-другому? К сожалению, бывает. Например:
Тут тоже всё логично: чем больше степень, тем больше раз число 0,5 умножается само на себя (т.е. делится пополам). Таким образом, полученная последовательность чисел убывает, а разница между первой и второй последовательностью состоит лишь в основании:
Суммируя эти факты, мы получаем самое главное утверждение, на котором и основано всё решение показательных неравенств:
Другими словами, если основание больше единицы, его можно просто убрать — знак неравенства при этом не поменяется. А если основание меньше единицы, то его тоже можно убрать, но при этом придётся поменять и знак неравенства.
С отрицательными основаниями всё ещё интереснее. Рассмотрим для примера вот такое неравенство:
На первый взгляд, всё просто:
В общем, ещё раз запомните главное правило: если основание в показательном уравнении больше единицы, его можно просто убрать; а если основание меньше единицы, его тоже можно убрать, но при этом поменяется знак неравенства.
Примеры решения
Итак, рассмотрим несколько простых показательных неравенств:
Что здесь можно сделать? Ну, слева у нас и так стоит показательное выражение — ничего менять не надо. А вот справа стоит какая-то хрень: дробь, да ещё и в знаменателе корень!
Однако вспомним правила работы с дробями и степенями:
Что это значит? Во-первых, мы легко можем избавиться от дроби, превратив её в степень с отрицательным показателем. А во-вторых, поскольку в знаменателе стоит корень, было бы неплохо превратить и его в степень — на этот раз с дробным показателем.
Применим эти действия последовательно к правой части неравенства и посмотрим, что получится:
Не забываем, что при возведении степени в степень показатели этих степеней складываются. И вообще, при работе с показательными уравнениями и неравенствами совершенно необходимо знать хотя бы простейшие правила работы со степенями:
Собственно, последнее правило мы только что и применили. Поэтому наше исходное неравенство перепишется следующим образом:
Теперь избавляемся от двойки в основании. Поскольку 2 > 1, знак неравенства останется прежним:
Вот и всё решение! Основная сложность — вовсе не в показательной функции, а в грамотном преобразовании исходного выражения: нужно аккуратно и максимально быстро привести его к простейшему виду.
Рассмотрим второе неравенство:
Так, так. Тут нас поджидают десятичные дроби. Как я уже много раз говорил, в любых выражениях со степенями следует избавляться от десятичных дробей — зачастую только так можно увидеть быстрое и простое решение. Вот и мы избавимся:
Перед нами вновь простейшее неравенство, да ещё и с основанием 1/10, т.е. меньшим единицы. Что ж, убираем основания, попутно меняя знак с «меньше» на «больше», и получаем:
Важное замечание. Данное неравенство можно было решить и по-другому — путём приведения обеих частей к степени с основанием, большим единицы. Взгляните:
После такого преобразования мы вновь получим показательное неравенство, но с основанием 10 > 1. А это значит, что можно просто зачеркнуть десятку — знак неравенства при этом не поменяется. Получим:
Как видите, ответ получился точь-в-точь такой же. При этом мы избавили себя от необходимости менять знак и вообще помнить какие-то там правила.:)
Идём далее. Рассмотрим чуть более сложное неравенство — в нём в показателе появляется квадратичная функция:
Ура! Мы получили обычное квадратное неравенство! Знак нигде не менялся, поскольку в основании стоит двойка — число, большее единицы.
Нули функции на числовой прямой
Наконец, рассмотрим ещё одно неравенство:
Опять видим показательную функцию с десятичной дробью в основании. Переводим эту дробь в обыкновенную:
В данном случае мы воспользовались приведённым ранее замечанием — свели основание к числу 5 > 1, чтобы упростить себе дальнейшее решение. Точно так же поступим и с правой частью:
Перепишем исходное неравенство с учётом обоих преобразований:
Основания с обеих сторон одинаковы и превосходят единицу. Никаких других слагаемых справа и слева нет, поэтому просто «зачёркиваем» пятёрки и получаем совсем простое выражение:
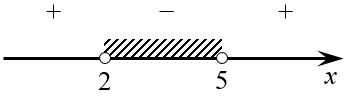
Однако работать с модулями — не самое приятное занятие, правда? Вот и мы не будем работать. А вместо этого просто перенесём все слагаемые влево и решим обычное неравенство методом интервалов:
Вновь отмечаем полученные точки на числовой прямой и смотрим знаки:
Обратите внимание: точки закрашены
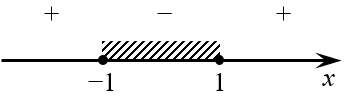
В целом хотел бы заметить, что ничего сложного в показательных неравенствах нет. Смысл всех преобразований, которые мы сегодня выполняли, сводится к простому алгоритму:
По сути, это универсальный алгоритм решения всех таких неравенств. А всё, что вам ещё будут рассказывать по этой теме — лишь конкретные приёмы и хитрости, позволяющие упростить и ускорить преобразования. Вот об одном из таких приёмов мы сейчас и поговорим.:)
Метод рационализации
Рассмотрим ещё одну партию неравенств:
Ну и что в них такого особенного? Они же лёгкие. Хотя, стоп! Число π возводится в какую-то степень? Что за бред?
Получается, что все эти «устрашающие» неравенства ничем не отличаются решаются от простых, рассмотренных выше? И решаются точно так же? Да, совершенно верно. Однако на их примере я хотел бы рассмотреть один приём, который здорово экономит время на самостоятельных работах и экзаменах. Речь пойдёт о методе рационализации. Итак, внимание:
Вот и весь метод.:) А вы думали, что будет какая-нибудь очередная дичь? Ничего подобного! Но этот простой факт, записанный буквально в одну строчку, значительно упростит нам работу. Взгляните:
Вот и нет больше показательных функций! И не надо помнить: меняется знак или нет. Но возникает новая проблема: что делать с грёбаным множителем \[\left( \text< >\!\!\pi\!\!\text< >-1 \right)\]? Мы ведь не знаем, чему равно точное значение числа π. Впрочем, капитан очевидность как бы намекает:
\[\text< >\!\!\pi\!\!\text< >\approx 3,14. \gt 3\Rightarrow \text< >\!\!\pi\!\!\text< >-1 \gt 3-1=2\]
Решаем неравенство методом интервалов
Перейдём к следующей задаче:
Тут вообще всё просто, потому что справа стоит единица. А мы помним, что единица — это любое число в нулевой степени. Даже если этим числом является иррациональное выражение, стоящее в основании слева:
Что ж, выполняем рационализацию:
\[\begin
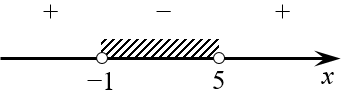
Получается, что второй множитель — не просто константа, а отрицательная константа! И при делении на неё знак исходного неравенства поменяется на противоположный:
Случай, когда нас интересуют боковые интервалы
Нас интересуют интервалы, отмеченные знаком «плюс». Осталось лишь записать ответ:
Переходим к следующему примеру:
Ну, тут совсем всё очевидно: в основаниях стоят степени одного и того же числа. Поэтому я распишу всё кратко:
Далее «причёсываем» выражения с обеих частей неравенства и применяем метод рационализации:
Как видим, в основании снова стоит иррациональное число, а справа снова стоит единица. Поэтому перепишем наше показательное неравенство следующим образом:
\[\begin
Переход к другому основанию
Отдельной проблемой при решении показательных неравенств является поиск «правильного» основания. К сожалению, далеко не всегда при первом взгляде на задание очевидно, что брать за основание, а что делать степенью этого основания.
Но не переживайте: здесь нет никакой магии и «секретных» технологий. В математике любой навык, который нельзя алгоритмизировать, можно легко выработать с помощью практики. Но для этого придётся решать задачи разного уровня сложности. Например, вот такие:
Сложно? Страшно? Да это же проще, чем цыплёнка об асфальт! Давайте попробуем. Первое неравенство:
Ну, я думают, тут и ежу всё понятно:
Переписываем исходное неравенство, сводя всё к основанию «два»:
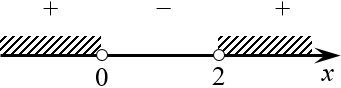
Да, да, вы всё правильно поняли: я только что применил метод рационализации, описанный выше. Теперь нужно работать аккуратно: у нас получилось дробно-рациональное неравенство (это такое, у которого в знаменателе стоит переменная), поэтому прежде чем что-то приравнивать к нулю, необходимо привести всё к общему знаменателю и избавиться от множителя-константы.
Более сложный случай: три корня
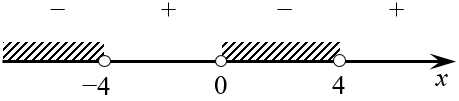
Как нетрудно догадаться, штриховкой отмечены те интервалы, на которых выражение слева принимает отрицательные значения. Поэтому в окончательный ответ пойдут сразу два интервала:
Концы интервалов не входят в ответ, поскольку исходное неравенство было строгим. Никаких дополнительных проверок этого ответа не требуется. В этом плане показательные неравенства намного проще логарифмических: никаких ОДЗ, никаких ограничений и т.д.
Переходим к следующей задаче:
Обратите внимание: в третьей строчке я решил не мелочиться и сразу разделить всё на (−2). Минул ушёл в первую скобку (теперь там везде плюсы), а двойка сократилась с множителем-константой. Именно так и стоит поступать при оформлении реальных выкладок на самостоятельных и контрольных работах — не надо расписывать прям каждое действие и преобразование.
Идём далее. В следующем задании нас поджидают десятичные дроби:
А что нужно делать с десятичными дробями в показательных неравенствах? Правильно: избавляться от них, переводя в обыкновенные. Вот и мы переведём:
Ну и что мы получили в основаниях показательных функций? А получили мы два взаимно обратных числа:
Таким образом исходное неравенство можно переписать так:
Разумеется, при умножении степеней с одинаковым основанием их показатели складываются, что и произошло во второй строчке. Кроме того, мы представили единицу, стоящую справа, тоже в виде степени по основанию 4/25. Осталось лишь выполнить рационализацию:
Наконец, последнее неравенство из текущего «комплекта»:
В принципе, идея решения тут тоже ясна: все показательные функции, входящие в состав неравенства, необходимо свести к основанию «3». Но для этого придётся немного повозиться с корнями и степенями:
С учётом этих фактов исходное неравенство можно переписать так:
Но вернёмся к нашей задаче. Попробуем в этот раз обойтись без рационализации. Вспоминаем: основание степени больше единицы, поэтому тройки можно просто зачеркнуть — знак неравенства при этом не поменяется. Получим:
Выделение устойчивого выражения и замена переменной
В заключение предлагаю решить ещё четыре показательных неравенства, которые уже являются довольно сложными для неподготовленных учеников. Чтобы справиться с ними, необходимо вспомнить правила работы со степенями. В частности — вынесение общих множителей за скобки.
Но самое главное — научиться понимать: что именно можно вынести за скобки. Такое выражение называется устойчивым — его можно обозначить новой переменной и таким образом избавиться от показательной функции. Итак, посмотрим на задачи:
Начнём с самой первой строчки. Выпишем это неравенство отдельно:
Вот примерно так и нужно оформлять решение на настоящих контрольных и самостоятельных работах.
Что ж, попробуем что-нибудь посложнее. Например, вот такое неравенство:
Первое, на что следует обратить внимание — это, конечно, десятичная дробь в основании первой степени. От неё необходимо избавиться, а заодно привести все показательные функции к одному и тому же основанию — числу «2»:
\[\begin
То же самое и с тройкой (числа 9, 27, 81 и 243 являются её степенями), и с семёркой (числа 49 и 343 тоже было бы неплохо запомнить). Ну, и у пятёрки тоже есть «красивые» степени, которые нужно знать:
Конечно, все эти числа при желании можно восстановить в уме, просто последовательно умножая их друг на друга. Однако, когда вам предстоит решить несколько показательных неравенств, причём каждое следующее сложнее предыдущего, то последнее, о чём хочется думать — это степени каких-то там чисел. И в этом смысле данные задачи являются более сложными, нежели «классические» неравенства, которые решаются методом интервалов.
Надеюсь, этот урок помог вам в освоении данной темы. Если что-то непонятно — спрашивайте в комментариях. И увидимся в следующих уроках.:)