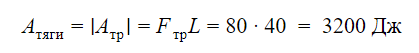Что такое полезная работа полная работа

Что такое полезная работа полная работа

При перемещении тела с помощью простых механизмов (рычагов, блоков, наклонной плоскости) приложенной силе приходится преодолевать не только вес самого груза.

Надо поднять груз с помощью подвижного блока на высоту.
Для поднятия груза человек прикладывает к веревке силу (F тяги).
Какую работу он при этом совершает?

Надо поднять непосредственно груз весом Р.
Кроме груза надо поднять еще веревку и блок весом Р бл.
Надо преодолеть трение о воздух и в осях блока, мешающее подьему.

1. Какую работу называют полной?

1. Какую работу называют полезной?

Совершаемая с помощью механизма полная работа всегда больше полезной работы.
Часть затрачиваемой работы расходуется на преодоление трения в оси механизма и сопротивления воздуха, а также на движение самого механизма.

3. Что такое коэффициент полезного действия механизма?

Отношение полезной работы к полной работе называется коэффициентом полезного действия.

Сокращенно коэффициент полезного действия обозначается КПД.

КПД обычно выражают числом или в процентах и обозначают греческой буквой, которая читается как «эта».

4. Может ли КПД быть больше единицы?

Полезная работа всегда меньше затраченной работы.

Поэтому КПД любого механизма всегда меньше 100% ( или меньше 1).

Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их вес.

4. Пример решения задачи на расчет КПД.

Задача.
На коротком плече рычага подвешен груз массой 100 кг.
Для его подъема к длинному плечу приложили силу 250 Н.
Груз подняли на высоту h₁ = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h₂ = 0,4 м.
Найти КПД рычага.

Источник

Понятие КПД: определение, формула и применение в физике

Физика — это наука, которая изучает процессы, происходящие в природе. Наука эта очень интересная и любопытная, ведь каждому из нас хочется удовлетворить себя ментально, получив знания и понимание того, как и что в нашем мире устроено. Физика, законы которой выводились не одно столетие и не одним десятком ученных, помогает нам с этой задачей, и мы должны только радоваться и поглощать предоставленные знания.

Но в то же время физика — наука далеко непростая, как, собственно, и сама природа, но разобраться в ней было бы очень интересно. Сегодня мы будем говорить о коэффициенте полезного действия. Мы узнаем, что такое КПД и зачем он нужен. Рассмотрим все наглядно и интересно.

Определение и расшифровка КПД

Расшифровка аббревиатуры — коэффициент полезного действия. Однако и такое толкование с первого раза может оказаться не особо понятным. Этим коэффициентом характеризуется эффективность системы или какого-либо отдельного тела, а чаще — механизма. Эффективность характеризуется отдачей или преобразованием энергии.

Этот коэффициент применим практически ко всему, что нас окружает, и даже к нам самим, причём в большей степени. Ведь совершаем мы полезную работу все время, только вот как часто и насколько это важно, уже другой вопрос, с ним и используется термин «КПД».

Важно учесть, что этот коэффициент — величина неограниченная, она, как правило, представляет собой либо математические значения, к примеру, 0 и 1, либо же, как это чаще бывает — в процентах.

В физике этот коэффициент обозначается буквой Ƞ, или, как её привыкли называть, Эта.

Полезная работа

При использовании каких-либо механизмов или устройств мы обязательно совершаем работу. Она, как правило, всегда больше той, что необходима нам для выполнения поставленной задачи. Исходя из этих фактов различается два типа работы: это затраченная, которая обозначается большой буквой, А с маленькой з (Аз), и полезная — А с буквой п (Ап). Для примера, возьмем такой случай: у нас есть задача поднять булыжник определенной массой на определенную высоту. В этом случае работа характеризует только преодоление силы тяжести, которая, в свою очередь, действует на груз.

В случае когда для подъема применяется какое-либо устройство, кроме силы тяжести булыжника, важно учесть еще и силу тяжести частей этого устройства. И кроме всего этого, важно помнить, что, выигрывая в силе, мы всегда будем проигрывать в пути. Все эти факты приводят к одному выводу, что затрачиваемая работа в любом варианте окажется больше полезной, Аз > Ап, вопрос как раз заключается в том, насколько её больше, ведь можно максимально сократить эту разницу и тем самым увеличить КПД, наш или нашего устройства.

Полезная работа — это часть затрачиваемой, которую мы совершаем, используя механизм. А КПД — это как раз та физическая величина, которая показывает, какую часть составляет полезная работа от всей затраченной.

Итог:

Физическая формула КПД

Существует определенная формула для нахождения КПД. Она звучит следующим образом: чтобы найти КПД в физике, нужно количество энергии разделить на проделанную системой работу. То есть КПД — это отношение затраченной энергии к выполненной работе. Отсюда можно сделать простой вывод, что тем лучше и эффективнее система или тело, чем меньше энергии затрачивается на выполнение работы.

Сама формула выглядит кратко и очень просто Ƞ будет равняться A/Q. То есть Ƞ = A/Q. В этой краткой формулы и фиксируют нужные нам элементы для вычисления. То есть A в этом случае является использованной энергией, которая потребляется системой во время работы, а большая буква Q, в свою очередь, будет являться затраченной A, или опять же затраченной энергией.

В идеале КПД равен единице. Но, как это обычно бывает, он её меньше. Так происходит по причине физики и по причине, конечно же, закона о сохранении энергии.

Все дело в том, что закон сохранения энергии предполагает, что не может быть получено больше А, чем получено энергии. И даже единице этот коэффициент будет равняться крайне редко, поскольку энергия тратится всегда. И работа сопровождается потерями: к примеру, у двигателя потеря заключается в его обильном нагреве.

Ƞ=А/Q, где

Применение в разных сферах физики

Примечательно, что КПД не существует как понятие нейтральное, для каждого процесса есть свой КПД, это не сила трения, он не может существовать сам по себе.

Рассмотрим несколько из примеров процессов с наличием КПД.

К примеру, возьмем электрический двигатель. Задача электрического двигателя — преобразовывать электрическую энергию в механическую. В этом случае коэффициентом будет являться эффективность двигателя в отношении преобразования электроэнергии в энергию механическую. Для этого случая также существует формула, и выглядит она следующим образом: Ƞ=P2/P1. Здесь P1 — это мощность в общем варианте, а P2 — полезная мощность, которую вырабатывает сам двигатель.

Нетрудно догадаться что структура формулы коэффициента всегда сохраняется, меняются в ней лишь данные, которые нужно подставить. Они зависят от конкретного случая, если это двигатель, как в случае выше, то необходимо оперировать затрачиваемой мощностью, если работа, то исходная формула будет другая.

Теперь мы знаем определение КПД и имеем представление об этом физическом понятии, а также об отдельных его элементах и нюансах. Физика — это одна из самых масштабных наук, но её можно разобрать на маленькие кусочки, чтобы понять. Сегодня мы исследовали один из этих кусочков.

Видео

Это видео поможет вам понять, что такое КПД.

Источник

Механическая работа

Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.

Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.

Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.

Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.

Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.

Механическая работа

А = FScosα

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

α — угол между векторами силы и перемещения []

Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.

Для совершения работы необходимы два условия:

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Полезная и затраченная работа

Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».

Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.

Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.

Потенциальная энергия

Е_п = mgh

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

h — высота [м]

На планете Земля g ≈ 9,8 м/с 2

Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).

Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

Мощность

На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.

Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.

Мощность

N = A/t

N — мощность [Вт]

A — механическая работа [Дж]

t — время [с]

Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.

Также для мощности справедлива другая формула:

Мощность

N = Fv

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.

Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:

Мощность

N = Fvcosα

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

α — угол между векторами силы и скорости []

Примеры решения задач

Задача 1

Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:

Решение

Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.

Ответ: 3.

Задача 2

Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?

Решение

Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:

Ответ: 3200 Дж.

Задача 3

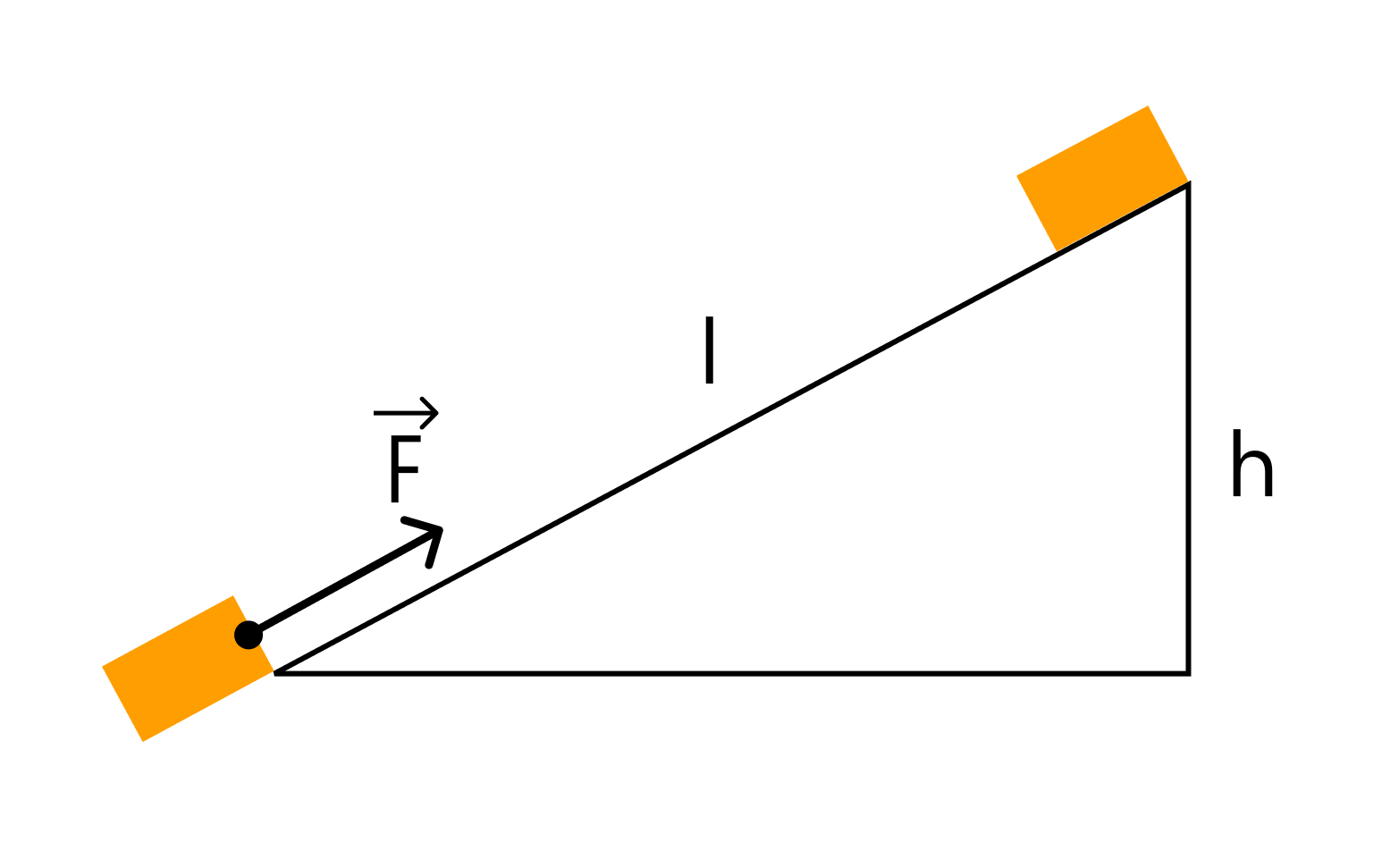
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?

Решение

В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.

Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:

A = Fl = 30 * 5 = 150 Дж

Ответ: 150 Дж.

Задача 4

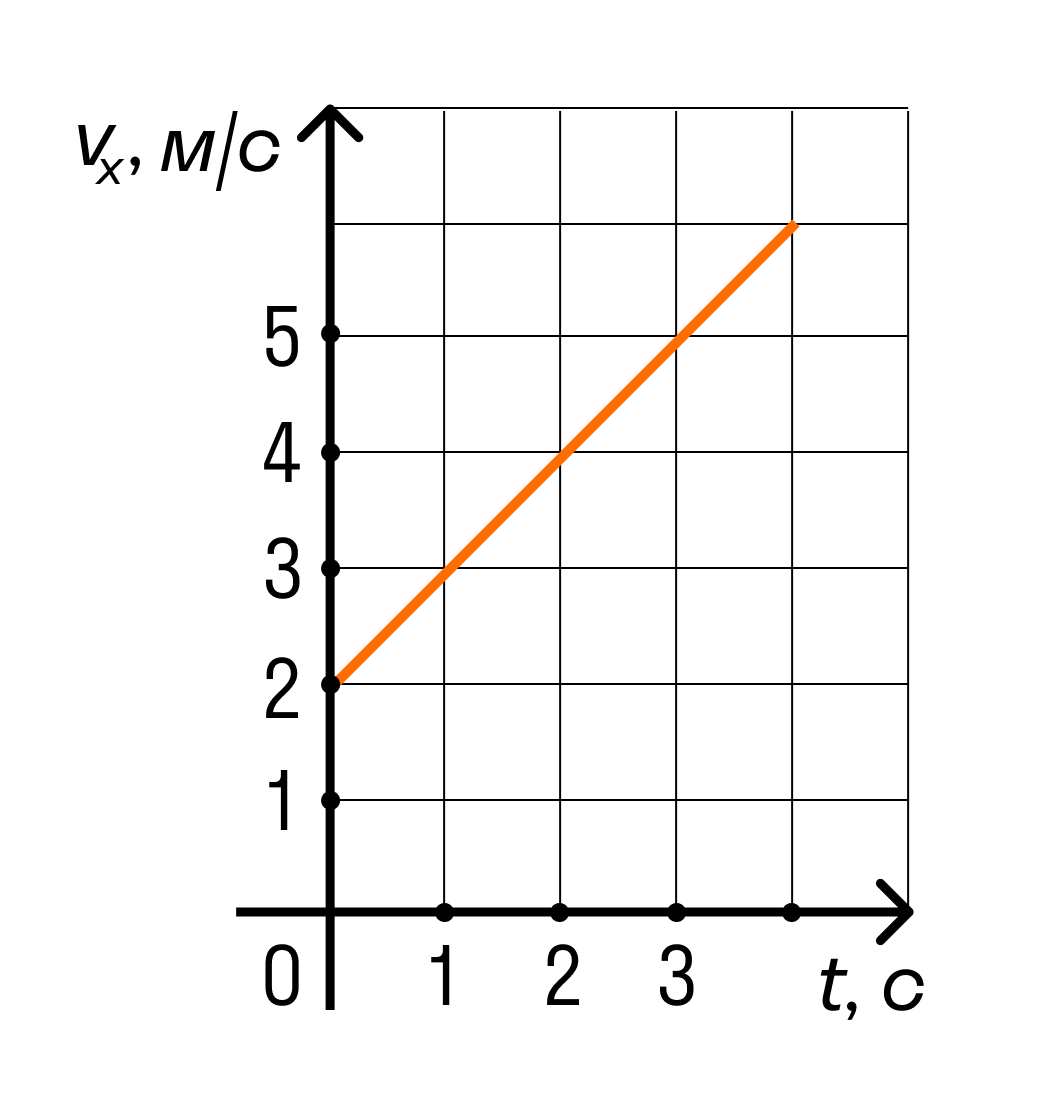
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?

Решение

На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.

Мощность можно найти по формуле N = Fv.

N = FV = 2×5 = 10 Вт

Ответ: 10 Вт.

Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!

Источник

КПД простых механизмов

п.1. Полезная работа и затраченная работа

Примеры полной и полезной работы

Затраченная работа равна сумме:

п.2. КПД механизма

Следовательно КПД реальных механизмов \(\eta\lt 100\text<%>\).

Только в идеальном механизме, в котором нет потерь на трение, и все составные элементы не имеют веса, \(A_\text<п>=A_\text<з>\) и \(\eta=100\text<%>\).

КПД никогда не может быть выше \(100\text<%>\).

КПД реальных механизмов можно увеличить за счет снижения трение в подвижных узлах и уменьшения веса всех составных элементов конструкции.

Для этого нужны новые смазочные вещества и лёгкие, но прочные конструкционные материалы.

п.3. Задачи

Задача 1. По наклонной плоскости поднимают груз массой 50 кг, прикладывая к нему силу 250 Н, направленную вдоль плоскости. Чему равен КПД плоскости, если её длина 10 м, а высота 3 м?

Полезная работа по подъему груза \begin A_\text<п>=mgh. \end Затраченная работа на перемещение груза вдоль наклонной плоскости \begin A_\text<з>=FL. \end КПД плоскости: \begin \eta=\frac>>\cdot 100\text<%>=\frac\cdot 100\text <%>\end Получаем: \begin \eta=\frac<50\cdot 10\cdot 3><250\cdot 10>\cdot 100\text<%>=60\text <%>\end Ответ: 60%

Задача 2. С помощью подвижного блока поднимают груз массой 200 кг, прикладывая силу 1200 Н. Чему равен КПД блока?

Полезная работа по подъему груза на высоту \(h\): \begin A_\text<п>=mgh. \end Подвижный блок дает выигрыш в силе в 2 раза и проигрыш в расстоянии. Т.е. при работе нужно вытянуть трос длиной \(2h\). Затраченная работа: \begin A_\text<з>=F\cdot 2h. \end КПД блока \begin \eta=\frac>>\cdot 100\text<%>=\frac<2Fh>\cdot 100\text<%>=\frac<2F>\cdot 100\text <%>\end Получаем: \begin \eta=\frac<200\cdot 10><2\cdot 1200>\cdot 100\text<%>\approx 83,3\text <%>\end Ответ: 83,3%

Задача 3. Груз массой 245 кг с помощью рычага равномерно подняли на высоту 6 см. При этом к длинному плечу рычага была приложена сила 500 Н, а точка приложения силы опустилась на 30 см. Найдите КПД рычага.

Полезная работа по подъему груза на высоту \(h_2\): \begin A_\text<п>=mgh_2. \end Затраченная работа по опусканию длинного плеча рычага: \begin A_\text<з>=F_1h_1. \end КПД рычага \begin \eta=\frac>>\cdot 100\text<%>=\frac\cdot 100\text <%>\end Получаем: \begin \eta=\frac<245\cdot 10\cdot 0,06><500\cdot 0,3>\cdot 100\text<%>=\frac<147><150>\cdot 100\text<%>=98\text <%>\end Ответ: 98%

Задача 5*. Груз массой 12 кг поднимают с помощью подвижного блока массой 3 кг. Чему равен КПД блока?

Полезная работа по подъему груза на высоту \(h\): \begin A_\text<п>=Mgh. \end Подвижный блок дает выигрыш в силе в 2 раза. Поэтому достаточно приложить силу, равную половине суммы весов груза и блока: \begin F=\frac 12(M+m)g \end При этом будет проигрыш в расстоянии. Потребуется вытянуть трос длиной \(2h\). Затраченная работа, приложенная к тросу: \begin A_\text<з>=F\cdot 2h=\frac 12(M+m)g\cdot 2h=(M+m)gh. \end КПД подвижного блока \begin \eta=\frac>>\cdot 100\text<%>=\frac<(M+m)gh>\cdot 100\text<%>=\frac\cdot 100\text <%>\end Получаем: \begin \eta=\frac<12><12+3>\cdot 100\text<%>=80\text <%>\end Ответ: 80%

Задача 6. Сколько воды можно поднять из колодца глубиной 36 м за 1 ч, если мощность электродвигателя равна 5 кВт, КПД всей установки равно 70%?
Дано:
\(N=5\ \text<кВт>=5\cdot 10^3\ \text<Вт>\)
\(\eta=70\text<%>=0,7\)
\(h=36\ \text<м>\)
\(t=1\ \text<ч>=3600\ \text<с>\)
\(g\approx 10\ \text<м/с>^2\)
__________________
\(m-?\)

Полезная работа по подъему груза на высоту \(h\): \begin A_\text<п>=Mgh. \end Затраченная работа электродвигателя: \begin A_\text<з>=Nt. \end КПД установки \begin \eta=\frac>>=\frac \end Масса воды \begin m=\frac<\eta Nt> \end Получаем: \begin m=\frac<0,7\cdot 5\cdot 10^3\cdot 3600><10\cdot 36>=35\cdot 10^3\ (\text<кг>)=35\ \text <т>\end Ответ: 35 т

Задача 7*. КПД подвижного блока при подъеме первого груза равен 80%, а при подъеме второго груза – 90%. Масса какого груза больше и во сколько раз? Трением в блоке можно пренебречь.
Дано:
\(\eta_1=80\text<%>=0,8\)
\(\eta_2=90\text<%>=0,9\)
__________________
\(\frac-?\)

КПД подвижного блока массой \(m\), с помощью которого поднимают груз массой \(M\) \begin \eta=\frac \end (см. Задачу 5 выше). Масса груза \begin \eta(M+m)=M\Rightarrow \eta m=(1-\eta)M\Rightarrow M=\frac<\eta><1-\eta>m \end Получаем: \begin M_1=\frac<0,8><1-0,8>m=4m,\\[6pt] M_2=\frac<0,9><1-0,9>m=9m \end Масса второго груза больше.
Отношение масс \begin \frac=\frac<9m><4m>=2,25\ (\text<раз>) \end Ответ: масса второго груза больше в 2,25 раз

п.4. Лабораторная работа №13. Определение КПД наклонной плоскости

Цель работы
Научиться проводить измерения и рассчитывать КПД простого механизма на примере наклонной плоскости. Исследовать зависимость КПД наклонной плоскости от высоты.

Вес \(P\) и сила \(F\) определяются в работе с помощью динамометра с ценой деления \(d=0,1\ \text<Н>\).

Сила \(F\) определяется в серии из пяти опытов с вычислением средних величин.

Высота наклонной плоскости \(h\) и длина наклонной плоскости \(L\) определяются с помощью мерной ленты с ценой деления \(d=5\ \text<мм>\). Абсолютная погрешность \(\Delta_L=2,5\ \text<мм>\).

Относительные погрешности измерений вычисляются как обычно.

Приборы и материалы
Доска длиной от 70 см, штатив с муфтой и лапкой, брусок массой не менее 300 г, мерная лента, динамометр.

Ход работы
1. Измерьте мерной лентой длину доски \(L\).
2. Определите вес бруска \(P\) с помощью динамометра.
3. Соберите наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около \(h=\frac L3.\)
4. Положите брусок на наклонную плоскость, прикрепите к нему динамометр и равномерно тяните по наклонной плоскости. Следите, чтобы динамометр располагался параллельно наклонной плоскости. Запишите измеренное значение \(F\). Повторите измерение \(F\) в серии из пяти опытов.
5. Соберите новую наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около \(h=\frac L4\). Перейдите на шаг 4 и повторите серию опытов для определения \(F\).
6. Рассчитайте КПД для двух исследованных наклонных плоскостей. Найдите относительные и абсолютные погрешности расчетов КПД.
7. Для каждой из наклонных плоскостей укажите величину полезной и затраченной работы, найдите силу трения.
8. Сделайте выводы о зависимости силы трения и КПД от высоты наклонной плоскости.

Результаты измерений и вычислений

Длина наклонной плоскости (доски) \begin L=80\ \text<см>=800\ \text<мм>,\\[7pt] \Delta_L=2,5\ \text<мм>,\\[6pt] \delta_L=\frac<\Delta_L>=\frac<2,5><800>\approx 0,0031=0,31\text <%>\end

Вес бруска \begin P=4,4\ \text<Н>,\\[7pt] \Delta_P=0,05\ \text<Н>,\\[6pt] \delta_P=\frac<\Delta_P>

=\frac<0,05><4,4>\approx 0,0011=1,1\text <%>\end

1. Наклонная плоскость высотой \(h=27\ \text<см>\)

Высота наклонной плоскости \begin h=27\ \text<см>=270\ \text<мм>,\\[7pt] \Delta_h=2,5\ \text<мм>,\\[6pt] \delta_h=\frac<\Delta_h>=\frac<2,5><270>\approx 0,0093=0,93\text <%>\end

Определение силы тяги \(F\) в серии опытов

2. Наклонная плоскость высотой \(h=20\ \text<см>\)

Высота наклонной плоскости \begin h=20\ \text<см>=200\ \text<мм>,\\[7pt] \Delta_h=2,5\ \text<мм>,\\[6pt] \delta_h=\frac<\Delta_h>=\frac<2,5><200>\approx 0,013=1,3\text <%>\end

Определение силы тяги \(F\) в серии опытов

Выводы
На основании полученных результатов можно сделать следующие выводы.

В работе проводился расчет КПД наклонной плоскости постоянной длины, но разной высоты.

Для высоты около \(h=\frac L3\):

Для высоты около \(h=\frac L4\):

Таким образом, с уменьшением высоты:

Все задачи, поставленные перед исследованием, успешно выполнены.

Источник