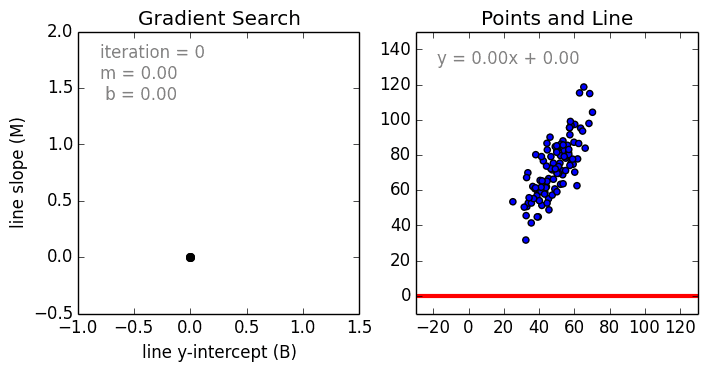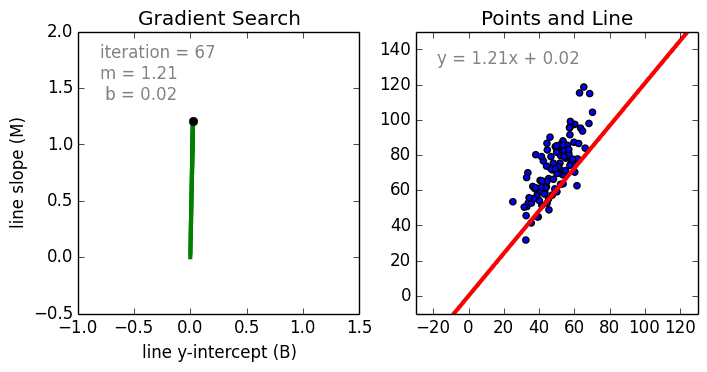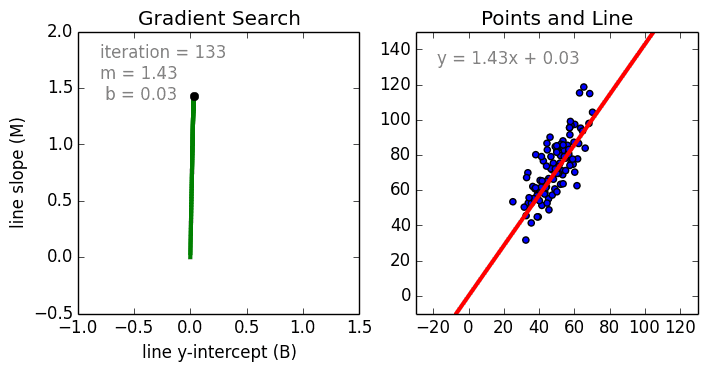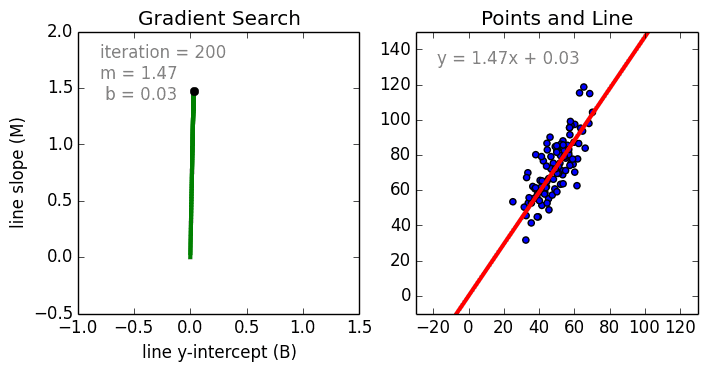
Что такое полиномиальная регрессия

5 видов регрессии и их свойства

Jan 16, 2019 · 5 min read

Линейная и логистическая регрессии обычно являются первыми видами регрессии, которые изучают в таких областях, как машинное обучение и наука о данных. Оба метода считаются эффективными, так как их легко понять и использовать. Однако, такая простота также имеет несколько недостатков, и во многих случаях лучше выбирать другую регрессионную модель. Существует множество видов регрессии, каждый из которых имеет свои достоинства и недостатки.

Мы познакомимся с 7 наиболее распростран е нными алгоритмами регрессии и опишем их свойства. Также мы узнаем, в каких ситуация и с какими видами данных лучше использовать тот или иной алгоритм. В конце мы расскажем о некоторых инструментах для построения регрессии и поможем лучше разобраться в регрессионных моделях в целом!

Линейная регрессия

Регрессия — это метод, используемый для моделирования и анализа отношений между переменными, а также для того, чтобы увидеть, как эти переменные вместе влияют на получение определенного результата. Линейная регрессия относится к такому виду регрессионной модели, который состоит из взаимосвязанных переменных. Начнем с простого. Парная (простая) линейная регрессия — это модель, позволяющая моделировать взаимосвязь между значениями одной входной независимой и одной выходной зависимой переменными с помощью линейной модели, например, прямой.

Более распространенной моделью является множественная линейная регрессия, которая предполагает установление линейной зависимости между множеством входных независимых и одной выходной зависимой переменных. Такая модель остается линейной по той причине, что выход является линейной комбинацией входных переменных. Мы можем построить модель множественной линейной регрессии следующим образом:

Y = a_1*X_1 + a_2*X_2 + a_3*X_3 ……. a_n*X_n + b

Несколько важных пунктов о линейной регрессии:

Полиномиальная регрессия

Для создания такой модели, которая подойдет для нелинейно разделяемых данных, можно использовать полиномиальную регрессию. В данном методе проводится кривая линия, зависимая от точек плоскости. В полиномиальной регрессии степень некоторых независимых переменных превышает 1. Например, получится что-то подобное:

Y = a_1*X_1 + (a_2)²*X_2 + (a_3)⁴*X_3 ……. a_n*X_n + b

У некоторых переменных есть степень, у других — нет. Также можно выбрать определенную степень для каждой переменной, но для этого необходимы определенные знания о том, как входные данные связаны с выходными. Сравните линейную и полиномиальную регрессии ниже.

Несколько важных пунктов о полиномиальной регрессии:

Гребневая (ридж) регрессия

В случае высокой коллинеарности переменных стандартная линейная и полиномиальная регрессии становятся неэффективными. Коллинеарность — это отношение независимых переменных, близкое к линейному. Наличие высокой коллинеарности можно определить несколькими путями:

Сначала можно посмотреть на функцию оптимизации стандартной линейной регрессии для лучшего понимания того, как может помочь гребневая регрессия:

Где X — это матрица переменных, w — веса, y — достоверные данные. Гребневая регрессия — это корректирующая мера для снижения коллинеарности среди предикторных переменных в регрессионной модели. Коллинеарность — это явление, в котором одна переменная во множественной регрессионной модели может быть предсказано линейно, исходя из остальных свойств со значительной степенью точности. Таким образом, из-за высокой корреляции переменных, конечная регрессионная модель сведена к минимальным пределам приближенного значения, то есть она обладает высокой дисперсией.

Гребневая регрессия добавляет небольшой фактор квадратичного смещения для уменьшения дисперсии:

Такой фактор смещения выводит коэффициенты переменных из строгих ограничений, вводя в модель небольшое смещение, но при этом значительно снижая дисперсию.

Несколько важных пунктов о гребневой регрессии:

Регрессия по методу «лассо»

В регрессии лассо, как и в гребневой, мы добавляем условие смещения в функцию оптимизации для того, чтобы уменьшить коллинеарность и, следовательно, дисперсию модели. Но вместо квадратичного смещения, мы используем смещение абсолютного значения:

Существует несколько различий между гребневой регрессией и лассо, которые восстанавливают различия в свойствах регуляризаций L2 и L1:

Регрессия «эластичная сеть»

Эластичная сеть — это гибрид методов регрессии лассо и гребневой регрессии. Она использует как L1, так и L2 регуляризации, учитывая эффективность обоих методов.

min || Xw — y ||² + z_1|| w || + z_2|| w ||²

Практическим преимуществом использования регрессии лассо и гребневой регрессии является то, что это позволяет эластичной сети наследовать некоторую стабильность гребневой регрессии при вращении.

Несколько важных пунктов о регрессии эластичной сети:

Вывод

Вот и все! 5 распространенных видов регрессии и их свойства. Все данные методы регуляризации регрессии (лассо, гребневая и эластичной сети) хорошо функционирует при высокой размерности и мультиколлинеарности среди переменных в наборе данных.

Источник

Полиномиальная регрессия

Дата публикации Oct 8, 2018

Это мой третий блог в серии машинного обучения. Этот блог требует предварительных знаний о линейной регрессии. Если вы не знаете о линейной регрессии или нуждаетесь в обновлении, просмотрите предыдущие статьи этой серии.

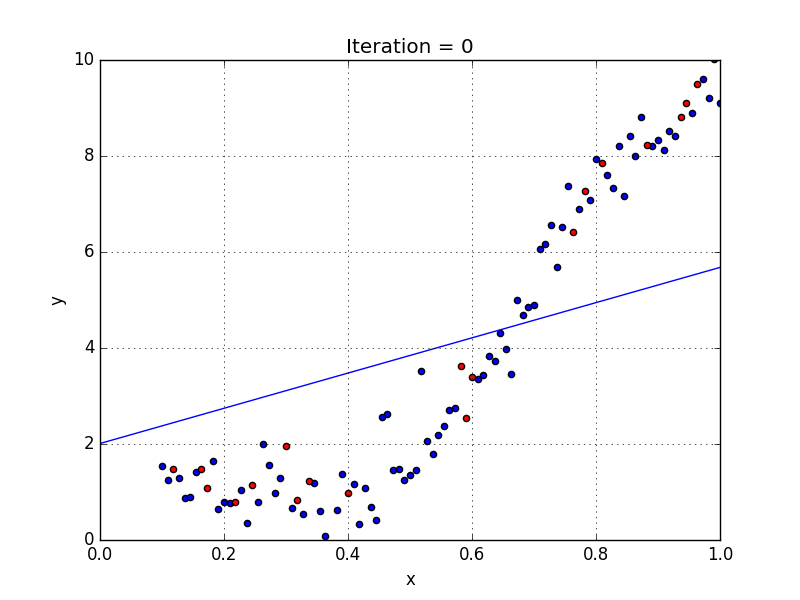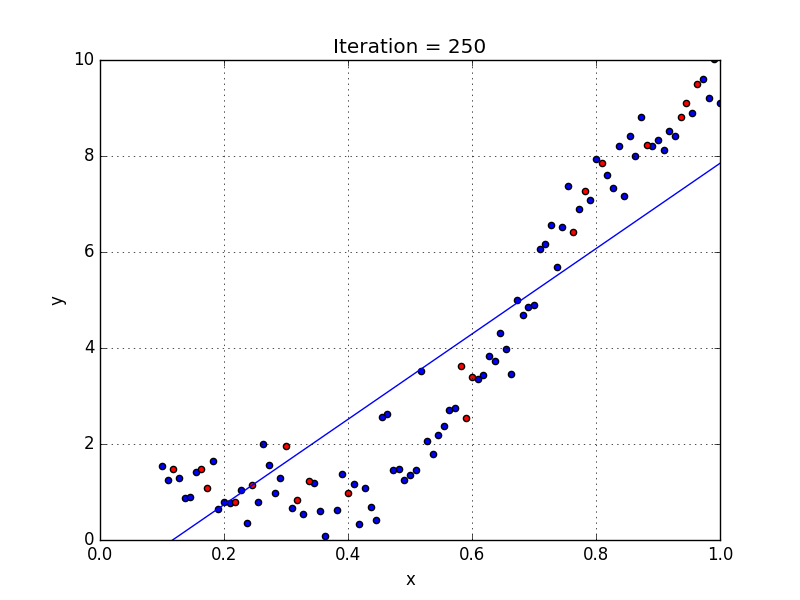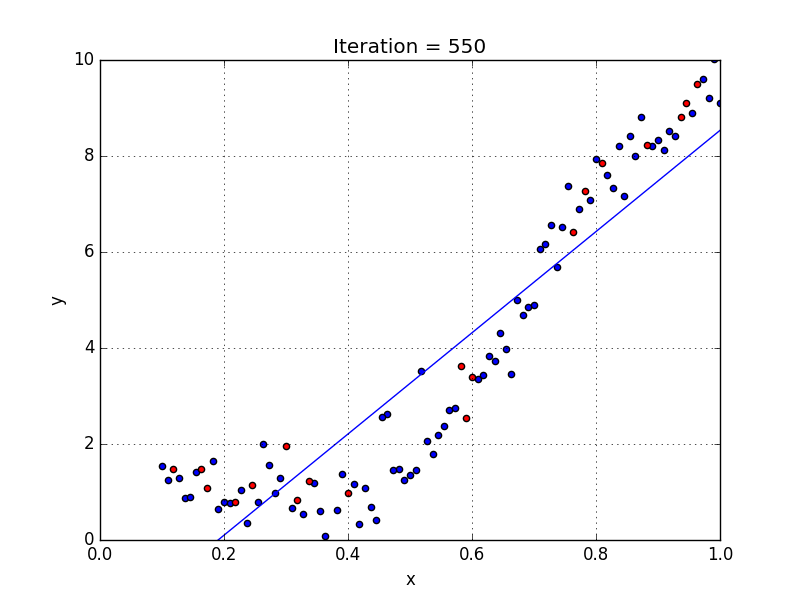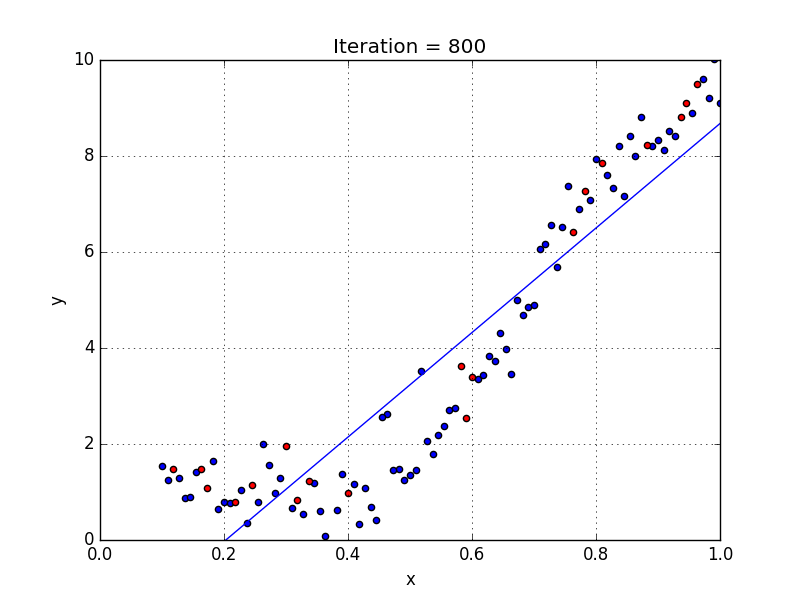
Линейная регрессия требует, чтобы отношение между зависимой переменной и независимой переменной было линейным. Что если распределение данных было более сложным, как показано на рисунке ниже? Можно ли использовать линейные модели для подбора нелинейных данных? Как мы можем создать кривую, которая лучше всего отражает данные, как показано ниже? Что ж, мы ответим на эти вопросы в этом блоге.

Оглавление

Почему полиномиальная регрессия?

Чтобы понять необходимость полиномиальной регрессии, давайте сначала сгенерируем случайный набор данных.

Сгенерированные данные выглядят как

Давайте применим модель линейной регрессии к этому набору данных.

Сюжет самой подходящей линии

Мы можем видеть, что прямая линия не может захватить шаблоны в данных. Это примерпод-фитинга, Вычисление RMSE и R²-показателя линейной линии дает:

Чтобы преодолеть несоответствие, нам нужно увеличить сложность модели.

Чтобы сгенерировать уравнение более высокого порядка, мы можем добавить мощности оригинальных функций в качестве новых. Линейная модель,

может быть преобразован в

Это все еще считаетсялинейная модельпоскольку коэффициенты / веса, связанные с признаками, все еще линейны. x² это только особенность. Однако кривая, которая нам подходитквадратныйв природе.

Подгонка модели линейной регрессии к преобразованным объектам дает график ниже.

Из графика совершенно ясно, что квадратичная кривая может соответствовать данным лучше, чем линейная линия. Вычисление RMSE и R²-балла квадратичного графика дает:

Мы можем видеть, что среднеквадратичное отклонение уменьшилось, а показатель R² увеличился по сравнению с линейной линией

Если мы попытаемся подогнать кубическую кривую (степень = 3) к набору данных, мы увидим, что он проходит через больше точек данных, чем квадратичный и линейный графики.

Метрика кубической кривой

Ниже приведено сравнение подгонки линейных, квадратичных и кубических кривых к набору данных.

Если мы продолжим увеличивать степень до 20, мы увидим, что кривая проходит через большее количество точек данных. Ниже приведено сравнение кривых для степени 3 и 20.

Для степени = 20 модель также фиксирует шум в данных. Это примернад-фитинга, Даже если эта модель проходит через большую часть данных, она не сможет обобщить невидимые данные.

Чтобы избежать перестройки, мы можем добавить больше обучающих выборок, чтобы алгоритм не распознавал шум в системе и мог стать более обобщенным.(Примечание: добавление дополнительных данных может быть проблемой, если данные сами по себе являются помехами).

Как выбрать оптимальную модель? Чтобы ответить на этот вопрос, нам нужно понять компромисс между компромиссом и дисперсией.

Компромисс против дисперсии

предвзятостьотносится к ошибке из-за упрощенных предположений модели при подборе данных. Высокое смещение означает, что модель не может захватить шаблоны в данных, и это приводит кпод-фитинга,

отклонениеотносится к ошибке из-за сложной модели, пытающейся соответствовать данным. Высокая дисперсия означает, что модель проходит через большинство точек данных, и это приводит кнад-фитингаданные.

На картинке ниже представлены результаты нашего обучения.

Из рисунка ниже мы можем наблюдать, что с увеличением сложности модели смещение уменьшается, а дисперсия увеличивается, и наоборот. В идеале модель машинного обучения должна иметьнизкая дисперсия и низкий уклон, Но практически невозможно иметь оба. Поэтому, чтобы получить хорошую модель, которая хорошо работает как на поездах, так и на невидимых данных,компромисссделан.

До сих пор мы рассмотрели большую часть теории полиномиальной регрессии. Теперь давайте реализуем эти концепции в наборе данных Boston Housing, который мы проанализировали впредыдущийблог.

Применение полиномиальной регрессии к набору данных Housing

Давайте определим функцию, которая преобразует исходные элементы в полиномиальные элементы заданной степени, а затем применяет к ним линейную регрессию.

Далее мы вызываем вышеуказанную функцию со степенью 2.

Производительность модели с использованием полиномиальной регрессии:

Это лучше, чем мы достигли с помощью линейной регрессии впредыдущийблог.

Вот и все для этой истории. Это GithubСделки рЕПОсодержит весь код для этого блога, и можно найти полный блокнот Jupyter, используемый для набора данных жилья в БостонеВот,

Вывод

В этой серии машинного обучения мы рассмотрели линейную регрессию, полиномиальную регрессию и реализовали обе эти модели в наборе данных Boston Housing.

Мы расскажем о логистической регрессии в следующем блоге.

Источник

Полиномиальная регрессия и метрики качества модели

Давайте разберемся на примере. Скажем, я хочу спрогнозировать зарплату специалиста по данным на основе количества лет опыта. Итак, моя целевая переменная (Y) — это зарплата, а независимая переменная (X) — опыт. У меня есть случайные данные по X и Y, и мы будем использовать линейную регрессию для прогнозирования заработной платы. Давайте использовать pandas и scikit-learn для загрузки данных и создания линейной модели.

Из приведенного выше графика мы видим, что существует разрыв между прогнозируемыми и фактическими точками данных. Получается, что линейная функция не может достаточно хорошо описать наши данные. Исходя из жизненного опыта, мы так же можем предположить, что увеличение зарплаты сотрудника происходит не линейно, а в зависимости от опыта работы: чем больше опыт – тем больше повышение!

Статистически разрыв / разница между графиками называется остатками и обычно является ошибкой в RMSE и MAE.

Среднеквадратичная ошибка (RMSE) и средняя абсолютная ошибка (MAE) — это метрики, используемые для оценки работы модели регрессии. Эти показатели говорят нам, насколько точны наши прогнозы и какова величина отклонения от фактических значений.

Технически, RMSE — это корень среднего квадрата ошибок, а MAE — это среднее абсолютное значение ошибок. Здесь ошибки — это различия между предсказанными значениями (значениями, предсказанными нашей регрессионной моделью) и фактическими значениями переменной. По своей сути разница лишь в том, что RMSE из-за квадрата в формуле будет сильнее наказывать нас за ошибку, т.е. будет увеличивать вес / значение самой ошибки. Метрики рассчитываются следующим образом:

Yi – настоящее значение

Yp – предсказанное значение

n – кол-во наблюдений

Scikit-learn предоставляет библиотеку показателей для расчета этих значений. Однако мы будем вычислять RMSE и MAE, используя приведенные выше математические выражения. Оба метода дадут одинаковый результат.

Давайте попробуем составить полиномиальное преобразование (X) и совершить предсказание с той же моделью, чтобы посмотреть, уменьшатся ли наши ошибки. Для этого используем Scikit-learn PolynomialFeatures

То же действие можно сделать вручную и для любой степени полинома:

На этот раз они намного ниже. Давайте построим графики y и yp (как мы делали раньше), чтобы проверить совпадение:

Разрыв между двумя строками уменьшился, а метрики качества модели стали лучше!

Давайте разберем подобную задачу не на искусственных, а на реальных данных. Посмотрим на уже предобработанные данные по входам в систему онлайн трейдинга.

В переменной y_train хранится количество людей, зашедших во время x_train. Вполне обычная задача, решаемая линейной регрессией:

Модель отработала с ошибками MAE и RMSE в 0.602 и 0.616 соответственно. Такое высокое число ошибок связанно с тем, что данные имеют сильный разброс относительно линии регрессии. Однако, мы можем предположить, что для такого примера так же недостаточно лишь функции линейной регрессии. Давайте проверим эту гипотезу и попробуем применить полиномиальную регрессию и посмотреть метрики качества модели для полинома 2 степени:

Данная же модель отработала с ошибками MAE и RMSE в 0.498 и 0.543 соответственно, и визуально мы можем интерпретировать, что наша модель лучше стала описывать данные.

Почему же не использовать функцию большего количества степеней, 3, 15, 100? Ведь тогда метрики качества модели будут лишь улучшаться! Но не все так просто. Конечно, модель лучше станет описывать наши данные, а при совсем большом количестве степеней график станет аналогичен изначальному графику, но обобщающая способность модели сильно снизится, и она будет работать хорошо только лишь в данном наборе данных и не сможет должным образом сделать predict новых значений.

Таким образом мы разобрались в основных метриках качества работы модели и на их примере показали, что использование полиномиальной регрессии зачастую дает лучшие результаты, чем линейная. Однако всегда нужно отталкиваться от поставленной задачи.

Хочу отметить, что повысить метрики качества модели MAE и RMSE можно и другими способами. Некоторые из методов, которые мы можем использовать, включают в себя:

Источник

Русские Блоги

Основы машинного обучения-6. Полиномиальная регрессия

1. Полиномиальная регрессия

1. Мысль

Ограничение линейной регрессии заключается в том, что ее можно применять только к данным, имеющим линейную связь, но в реальной жизни многие данные имеют нелинейную связь. Хотя линейную регрессию также можно использовать для подбора нелинейной регрессии, эффект будет очень слабым. В настоящее время необходимо улучшить модель линейной регрессии, чтобы она могла соответствовать нелинейным данным.

2. Реализация кода

Подготовьте данные и введите случайный шум.

Во-первых, используется линейная регрессия.

Теперь используется полиномиальная регрессия.

3.sklearn

sklearn также инкапсулирует инструменты для добавления элементов функций в образцы в модуле предварительной обработки данных.

Когда PolynomialFeatures (степень = 3), выборка из 10 элементов будет сгенерирована для выборки с изначально двумя функциями. Конкретный метод генерации можно нарисовать из рисунка ниже, и он не будет здесь резюмирован.

4.pipeline

Конвейер может инкапсулировать тот же процесс для упрощения кода.

Два, переоборудованные и недогруженные

Переобучение относится к переобучению данных. Хотя полученная модель обучения очень хорошо соответствует обучающим данным, она будет плохо работать с данными тестирования. Причина в том, что переобучение приведет к Также сильно присутствует шум.

Теперь продолжайте изменять значение градуса и наблюдайте за результатом настройки.

Степень = 30, можно обнаружить, что, хотя данные хорошо подогнаны, на самом деле они не соответствуют фактическому тренду данных.

Недостаточная подгонка означает, что данные недостаточно обучены, а подгонка слишком проста, чтобы полностью выразить взаимосвязь данных, как показано на рисунке ниже.

3. Способность модели к обобщению.

При избыточной и недостаточной подгонке обученная модель будет иметь большое отклонение между прогнозируемым значением и истинным значением для новой выборки данных. В это время способность модели к обобщению невысока, то есть способность прогнозирования низкая; После надлежащего обучения и, наконец, способности делать более точные прогнозы для новых выборок данных, можно сказать, что способность модели к обобщению лучше. Цель состоит в том, чтобы обучить модель с хорошей способностью к обобщению, а не модель, которая хорошо соответствует обучающим данным.

Как правило, набор данных делится на набор обучающих данных и набор тестовых данных. Модель, обученная на наборе обучающих данных, также дает хорошие результаты на наборе обучающих данных. В настоящее время можно сказать, что способность модели к обобщению высока. Затем среднеквадратическая ошибка используется для измерения способности модели к обобщению. Чем меньше среднеквадратичная ошибка, тем сильнее способность к обобщению.

1. Линейная регрессия

Окончательный результат: 2.2199965269396573.

2. Полиномиальная регрессия

Окончательный результат: 0.8035641056297901. Когда степень = 30, результат будет 16,91453591949335, и способность к обобщению значительно снижается.

3. Кривая обучения

Кривая обучения может показать: по мере постепенного увеличения обучающих выборок производительность модели, обученной алгоритмом.

Из кривой обучения можно определить, что при непрерывном увеличении обучающих выборок среднеквадратичная ошибка обучающих данных сначала возрастает, а затем уменьшается, а среднеквадратичная ошибка тестовых данных продолжает расти, и в итоге обе имеют стабильное значение.

Инкапсулируйте приведенный выше код.

Для алгоритмов линейной регрессии.

Для алгоритмов полиномиальной регрессии.

Четыре, перекрестная проверка

1. Причины перекрестной проверки

как показано на картинке. Чтобы получить модель с сильной способностью к обобщению, данные делятся на тестовые данные и обучающие данные.Когда модель также хорошо подгоняет тестовые данные, можно сказать, что обобщающая способность модели сильна. Однако проблема все еще существует. Если модель, полученная на основе обучающих данных, не оказывает хорошего влияния на тестовые данные, необходимо настроить параметры тестовых данных. Другими словами, это фактически делается для того, чтобы модель лучше соответствовала набору тестовых данных. Проблема в том, что модель, вероятно, будет превосходить набор тестовых данных. Для этого набор данных делится на три части, и вводится набор проверочных данных. Данные обучения используются для обучения, а данные проверки используются для проверки качества модели и корректировки гиперпараметров.Тестовые данные используются в качестве последнего критерия.

Но существует также проблема чрезмерной подгонки данных проверки, поэтому необходима случайная обработка, поэтому вводится перекрестная проверка. Как показано на рисунке ниже, обучающие данные делятся на несколько частей (например, 3 части), разделенные данные объединяются и интегрируются в обучающие данные и данные проверки. Каждая интеграция обучает другую модель, и три модели Индекс производительности усредняется и используется в качестве меры индекса производительности модели, полученной с помощью текущего алгоритма.

2. Реализация кода

Сначала используйте метод разделения.

Используйте перекрестную проверку.

Можно обнаружить, что это не то же самое, что лучшее значение, полученное с помощью приведенного выше разделения.Простой метод разделения, описанный выше, может быть только моделью с избыточной подгонкой. После получения лучших параметров теперь необходимо использовать данные x_test для проверки.

Таким образом, можно сказать, что точность окончательной модели, полученной с помощью трехсторонней перекрестной проверки, составляет 98, что является очень надежным.

Вот обзор поиска по сетке. CV здесь означает перекрестную проверку.

Перекрестная проверка может быть преобразована в перекрестную проверку с исключением по одному (loo-cv, cross-validation с исключением по одному). То есть имеется m выборок, m-1 выборок используется в качестве обучающих данных, и только одна остается в качестве окончательного прогноза. В настоящее время он не будет зависеть от случайности и будет максимально приближен к реальному показателю производительности модели, но недостатки очевидны, и объем вычислений будет очень большим.

Пятерка, компромисс смещения и дисперсии

Ошибка модели = дисперсия + отклонение + неизбежная ошибка (например, потеря точности и шум, вызванный измерением)

Причина расхождения обычно заключается в том, что модель слишком сложна, и небольшое дрожание данных повлияет на результаты. Переобучение является основной причиной высокой дисперсии.

Непараметрическое обучение обычно отличается высокой дисперсией, поскольку на основании данных не делается никаких предположений. Например, KNN и деревья решений сильно зависят от выборочных данных.

Изучение параметров обычно представляет собой алгоритм с высокой систематической погрешностью из-за сильных допущений о данных, таких как линейная регрессия.

Смещение и дисперсия обычно противоречат друг другу, уменьшение смещения увеличивает дисперсию, а уменьшение дисперсии увеличивает смещение. В области алгоритмов основная проблема заключается в дисперсии.

Решения: снизить сложность модели, уменьшить размер данных и уменьшить шум; увеличить количество выборок; использовать наборы проверки, регуляризацию модели и т. Д.

Шесть, регуляризация модели

1. Регуляризация хребтовой регрессии

Как показано на рисунке ниже, когда степень велика, модель склонна к переобучению. Конкретным проявлением является то, что определенные значения коэффициентов θ будут очень большими. Следовательно, модель необходимо регуляризовать: ограничьте размер параметров.

Примечание. Когда модель регуляризована, θ начинается с 1 вместо 0. Причина в том, что θ0 влияет только на общую высоту кривой и не ограничивается. α является гиперпараметром и может быть изменен. Такой способ ограничения размера параметра θ обычно называютРегрессия хребта。

2. Реализация кода регрессии Риджа

Во-первых, используя полиномиальную регрессию, вы можете увидеть переобучение.

Затем используйте полиномиальную регрессию с регуляризацией гребневой регрессии.

Измените значение альфа на 1,100,100000 соответственно. Видно, что линии постепенно становятся гладкими.Когда альфа большой, чтобы сделать целевую функцию маленькой, коэффициент будет близок к 0, так что будет получена прямая линия, которая почти параллельна.

3. регуляризация LASSO

Полное написание лассо: наименьшее абсолютное сжатие и регрессия оператора выбора.

4. реализация кода в лассо

Нарисованное изображение показывает, что изображение, аппроксимированное регрессией лассо, ближе к прямой линии. лассо стремится сделать часть значения θ равной 0, поэтому его можно выбрать как функцию, что является значением оператора выбора. Вот краткое введение в причины.

Как показано на рисунке выше, для гребневой регрессии при решении минимального значения целевой функции, предполагая, что альфа приближается к бесконечности, начальной точкой коэффициента является синяя точка, и она будет стремиться к 0 вдоль красной линии. В этом процессе θ всегда стоило того.

Для регрессии лассо, поскольку θ не дифференцируемо, его можно записать только как кусочную функцию, как показано на рисунке выше.

Семерка, L1, L2 и эластичная сеть

1. Сравните регрессию гребня и регрессию лассо.

Здесь мы возвращаемся к дистанции Минковского.

Вышеупомянутая формула обобщается и выражается в следующей форме, и получаются регулярные члены L1 и L2, которые соответствуют лассо и регрессии гребня (но без квадратного корня, но также называемого L2).

На самом деле существует регулярный член L0, то есть есть надежда, что θ будет как можно меньше, и обычно он используется редко.

2. Эластичная сетка.

Значение эластичной сетки относительно просто, то есть регрессия гребня и регрессия лассо рассматриваются вместе, объединяя преимущества двух элементов и регулируя соотношение этих двух элементов с помощью r.

Интеллектуальная рекомендация

Измените имя хоста, сопоставьте IP-адрес и имя хоста, закройте вход в систему без пароля и пароля по selinux и SSH.

После изменения перезапустите виртуальный, и все будет в порядке. Чтобы мы могли соединяться друг с другом, не вводя IP-адрес в каждой виртуальной машине, мы должны сопоставить IP-адрес и имя хоста. З.

Уханьский университет предложил самый большой в мире набор данных масок, закрывающих лица (ссылка для скачивания прилагается): RMFD

Предисловие НедавниеПолучить COVID-19(Новая коронавирусная пневмония) Пострадавшие от эпидемии научные круги и промышленность последовательно использовали технологии искусственного интеллекта, чтобы п.

Источник