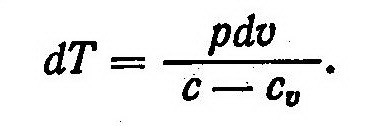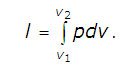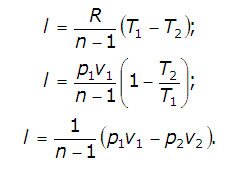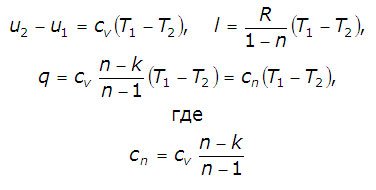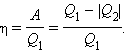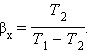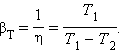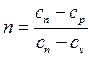Что такое политропа с переменным показателем

Политропный процесс

Здравствуйте! В процессах изменения состояния газа переменными часто являются все параметры состояния (температура, давление, удельный объем), причем в некоторых процессах может изменяться и теплоемкость. Для того чтобы рассчитать такой процесс, необходимо знать зависимость теплоемкости от параметров процесса. Расчет значительно упрощается, если теплоемкость считать постоянной. Политропным называют процесс, происходящий при постоянной теплоемкости и вызываемый подводом тепла к рабочему телу или отводом тепла от него (название происходит от греческих слов «поли» — много и «тропос» — путь). В политропном процессе в общем случае могут изменяться все параметры и функции состояния.

Для вывода уравнения политропного процесса продифференцируем уравнение Клапейрона :

Из выражений dq=du+pdυ и du=cudT найдем

Подставив в это соотношение равенство dq = cdT, будем иметь

Из выражения (3) найдем

После подстановки этого равенства в выражение (1) получим

Величину газовой постоянной определим из уравнения Майера cp = cυ + R.

Подставив величину R в выражение (4), и выполнив некоторые преобразования, найдем

Разделив уравнение (5) на pυ и введя обозначение

Интегрирование этого выражения возможно при условии n = const, то есть c=const. После интегрирования уравнения (7) получим

Выражение (8) называют уравнением политропы. Оно определяет связь между параметрами состояния p и υ в политропном процессе. Величина n, которая находится из соотношения (6), называется показателем политропы. Показатель n является функцией теплоемкости и, как и теплоемкость зависит от характера процесса. Для анализа частных случаев процесса требуется знать соответствующий показатель политропы n.

При изохорном процессе (c=cυ) функция (6) претерпевает бесконечный разрыв, изменяясь от n = +∞ до n — ∞. При изобарном процессе (с = ср) показатель n = 0. Следовательно, показатель политропы n в зависимости от характера процесса может изменяться в широких пределах, принимая любые значения от —∞ до +∞.
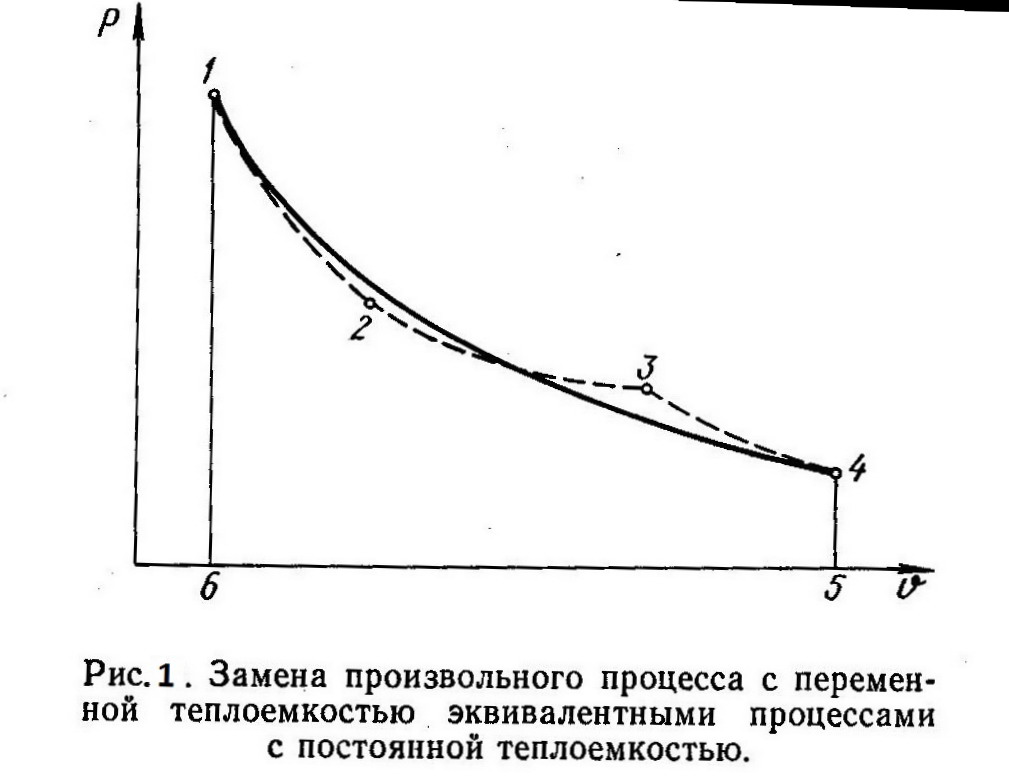
С помощью политропного процесса можно приближенно описать и рассчитать любой процесс изменения состояния 1—4 (рис. 1), для которого теплоемкость является переменной величиной. При этом произвольный процесс 1—4 необходимо заменить несколькими эквивалентными политропными процессами (процессы 1—2, 2—3 и 3—4), которые отличаются друг от друга постоянными значениями теплоемкости.

Замена должна производиться таким образом, чтобы работа в процессе 1—4 была равна работе на пути 1—2 — 3—4, то есть, чтобы были равны площади, ограниченные соответствующими кривыми процессов и ординатами 1—6 и 4—5. Так как изменение внутренней энергии ∆u на участке 1—4 не зависит от пути процесса (∆u=const), то, согласно уравнению q = ∆u + l первого закона термодинамики, количество теплоты в обоих случаях будет также одинаково. Погрешности, обусловленные такой заменой, окажутся тем меньшими, чем большим числом эквивалентных политропных участков будет заменен произвольный процесс 1—4, протекающий при переменной теплоемкости. Исп. литература: 1) Теплотехника, под общей ред. И.Н. Сушкина, Москва, «Металлургия», 1973. 2) Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,»Вышейшая школа», 1976.

Источник

Политропический процесс

Вы будете перенаправлены на Автор24

Что такое политропический процесс

Уравнение политропы для идеального газа

Получим уравнение политропы для идеального газа, следуя тому, что теплоемкость должна быть постоянна.

Из соотношения Майера:

\[C_p-C_V=\nu R\ \left(5\right).\]

Подставим (5) в (4), получим:

Очевидно, что если теплоемкость процесса постоянная, то

Уравнение интегрируем, потенцируем, получаем:

Запишем первое начало термодинамики:

\[CdT=\frac<2>\nu RdT+pdV\ \left(1.1\right).\]

Запишем уравнение процесса:

Подставим в (1.2) результаты преобразований (1.4) и (1.5), получим:

Готовые работы на аналогичную тему

Задание: Можно ли вычислить работу газа по формуле:

для адиабатного, изотермического и изобарного процессов?

Сравним с уравнением работы для адиабатного процесса, которое было рассмотрено в разделе, посвященном этому процессу, имеем:

Если учесть, что из уравнения Менделеева-Клайперона:

то получаем, что выражения (2.3) и (2.4) эквивалентны.

\[pV^0=const\ \to p=const\ \left(2.8\right).\]

Выражение (2.9) соответствует формуле вычисления работы для изобарного процесса.

Ответ: Данная формула подходит для вычисления работы в процессах: адиабатном и изобарном, не подходит для вычисления работы в изотермическом процессе.

Уравнение политропы имеет вид:

Подставим (3.3) вместо p (3.2), получим:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 26 11 2021

Источник

Политропный процесс

Содержание

Частные случаи [ править ]

Некоторые конкретные значения n соответствуют конкретным случаям:

Кроме того, когда применяется закон идеального газа :

Эквивалентность коэффициента политропы и отношения передачи энергии [ править ]

Для идеального газа в замкнутой системе, претерпевающего медленный процесс с незначительными изменениями кинетической и потенциальной энергии, процесс является политропным, так что

p v ( 1 − γ ) K + γ = C <\displaystyle pv^<(1-\gamma )K+\gamma >=C>

Отношение к идеальным процессам [ править ]

Для определенных значений индекса политропы этот процесс будет синонимом других общих процессов. Некоторые примеры влияния различных значений индекса приведены в следующей таблице.

Когда индекс n находится между любыми двумя из первых значений (0, 1, γ или ∞), это означает, что кривая политропы будет пересекать ( ограничиваться ) кривыми двух ограничивающих индексов.

Для идеального газа 1 γ = c p c v = c v + R c v = 1 + R c v = c p c p − R <\displaystyle \gamma =<\frac >>>=<\frac +R>>>=1+<\frac >>=<\frac >-R>>> .

Другое [ править ]

Источник

Политропный процесс

Политропным называется процесс, который описывается уравнением:

Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:

Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

представляет собой теплоемкость идеального газа в политропном процессе.

При c_v, k и n = const c_n = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

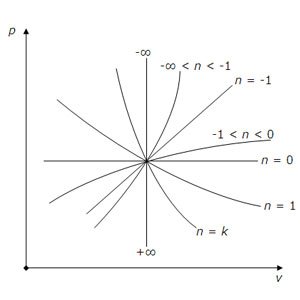
Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.

pv 0 = const (n = 0) – изобара;

pv = const (n = 1) – изотерма;

p 0 v = const, p 1/∞ v = const, pv ∞ = const – изохора;

pv k = const (n = k) – адиабата.

n > 0 – гиперболические кривые,

n

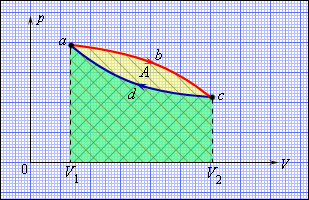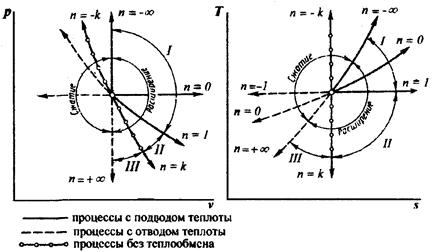
Рисунок 3.11.1. Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd

Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q₁ > 0 и отдает холодильнику количество теплоты Q₂

Коэффициент полезного действия указывает, какая часть тепловой энергии, полученной рабочим телом от «горячего» теплового резервуара, превратилась в полезную работу. Остальная часть (1 – η) была «бесполезно» передана холодильнику. Коэффициент полезного действия тепловой машины всегда меньше единицы (η 0, A > 0, Q₂ T₂

В двигателях, применяемых в технике, используются различные круговые процессы. На рис. 3.11.3 изображены циклы, используемые в бензиновом карбюраторном и в дизельном двигателях. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.

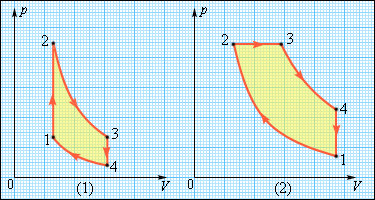Рисунок 3.11.3. Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2)

В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).

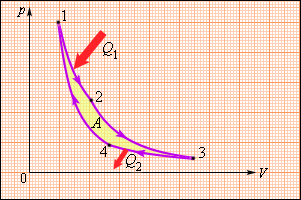Рисунок 3.11.4. Цикл Карно

Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T₁. Газ изотермически расширяется, совершая работу A₁₂, при этом к газу подводится некоторое количество теплоты Q₁ = A₁₂. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A₂₃ > 0. Температура газа при адиабатическом расширении падает до значения T₂. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T₂ 0, T₁ > T₂

Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q₂| от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением

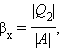т. е. эфективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении β_х может быть и больше, и меньше единицы. Для обращенного цикла Карно

Если полезным эффектом является передача некоторого количества тепла |Q₁| нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность β_Т теплового насоса может быть определена как отношение

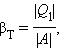т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:

следовательно, β_Т всегда больше единицы. Для обращенного цикла Карно

42. Холодильные машины

В основе работы холодильников лежит холодильный цикл. Простой паровой цикл механической холодильной машины реализуется с помощью четырех элементов, образующих замкнутый холодильный контур, – компрессора, конденсатора, дроссельного вентиля и испарителя или охладителя (рис. 1). Пар из испарителя поступает в компрессор и сжимается, вследствие чего его температура повышается. После выхода из компрессора пар, имеющий высокие температуру и давление, поступает в конденсатор, где охлаждается и конденсируется. В некоторых конденсаторах используется режим переохлаждения, т.е. дальнейшее охлаждение сконденсировавшейся жидкости ниже ее температуры кипения. Из конденсатора жидкость проходит через дроссельный вентиль. Поскольку температура кипения (насыщения) для данного давления оказывается ниже температуры жидкости, начинается ее интенсивное кипение; при этом часть жидкости испаряется, а температура оставшейся части опускается до равновесной температуры насыщения (тепло жидкости расходуется на ее превращение в пар). Процесс дросселирования иногда называют внутренним охлаждением или самоохлаждением, поскольку в этом процессе температура жидкого хладагента снижается до нужного уровня. Таким образом, из дроссельного вентиля выходят насыщенная жидкость и насыщенный пар. Насыщенный пар не может эффективно отводить тепло, поэтому он перепускается мимо испарителя и подается прямо на вход компрессора. Между дросселем и испарителем установлен сепаратор, в котором пар и жидкость разделяются.

Источник

Политропный процесс

Политропный процесс характеризуется тем, что он протекает в идеальном газе при постоянном значении теплоемкости, которая может иметь любое числовое значение от – ∞ до + ∞.

Для политропного процесса доля количества теплоты, расходуемой на из­менение внутренней энергии, остается неизменной:

. (4.36)

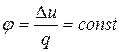
Выведем уравнение политропы. Пусть с_n – теплоемкость политропного процесса. В соответствии с уравнениями (dL = pdV, dq = du + dL, dq_v = du = с_vdT) получим:

. (4.37)

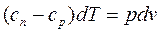
Используя уравнение (dh = du + pdv + vdp = dq + vdp), после ряда преобразований будем иметь:

. (4.38)

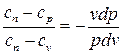
Так как из определения политропного процесса следует, что теплоемкость – величина постоянная, то обозначив

, (4.39)

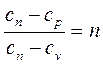
после интегрирования получим:

. (4.40)

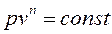
Это уравнение называется уравнением политропного процесса, а n – показателем политропы.

Для политропы справедлива следующая связь между основными параметрами состояния:

(4.41)

(4.42)

(4.43)

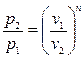
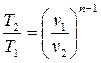
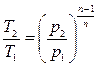
Работу политропного процесса можно определить по формулам:

; (4.44)

; (4.45)

; (4.46)

; (4.47)

. (4.48)

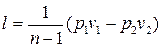
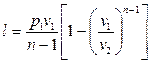
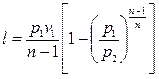
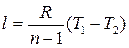
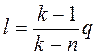
Для определения работы М кг газа нужно в приведенных фор­мулах заменить удельный объем v полным объемом газа V.

Теплоемкость политропного процесса можно найти из уравне­ния:

. (4.49)

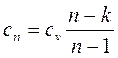
Количество теплоты, сообщаемой газу или отнимаемой от него:

; (4.50)

. (4.51)

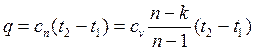
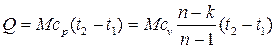
Изменение внутренней энергии газа в политропном процессе находим по общей для всех процессов формуле:

. (4.52)

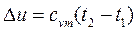
Показатель политропного процесса определяется из уравнения:

Изменение энтропии:

. (4.53)

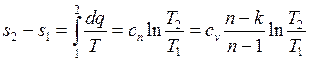
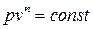
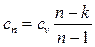
Политропный процесс включает в себя всю совокупность ос­новных термодинамических процессов и поэтому имеет и обоб­щающее значение. На самом деле из уравнений и нетрудно прийти к выводу, что:

при n = ± ∞ с_n = с_v и v = const (изохорный процесс);

при n = 0 с_n = с_p и р = const (изобарный процесс);

при n = 1 с_n = ∞ и рv = const (изотермный процесс);

при n = k с_n = 0 и pv k = const (адиабатный процесс).

На рисунке 4.5 в pv – и Ts – координатах приведены совмещенные графические зависимости различных термодинамических процес­сов.

Все процессы можно разделить на три группы (рисунок 4.5).

Группа I (– ∞

Теплоемкость отрицательна. Это хорошо видно из формулы 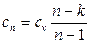. Так как с_n= dq/dT, то отрицательная с_n означает, что dq и dT имеют противоположные знаки. Несмотря на подвод к газу теплоты, его температура падает, и наоборот. В та­ких процессах l > q, поскольку на совершение работы помимо под­водимой теплоты расходуется часть внутренней энергии газа и его температура понижается.

Рис. 4.5 – Политропные процессы в pv и Тs – координатах

Группа III (+ ∞ > n > k). Графики этих процессов располагаются между адиабатой и изохорой. При расширении газа процесс осуще­ствляется с уменьшением внутренней энергии, с совершением ра­боты и отводом тепла в холодильник. С увеличением показателя n увеличивается доля теплоты, отводимой в холодильник, и умень­шается доля теплоты, идущей на совершение работы. Теплоем­кость положительна. Доля теплоты, расходуемой на совершение работы, уменьшается с ∞ до 0, а доля внутренней энергии, расхо­дуемой на совершение работы, с –1до 0.

Источник