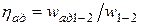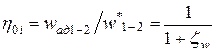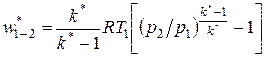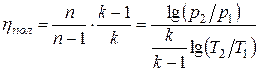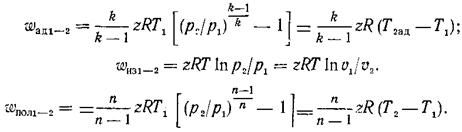Что такое политропный кпд

Коэффициент полезного действия компрессорных машин

Для анализа необратимых потерь в процессе сжатия используют понятие относительного КПД.

Относительный КПД – отношение работы в обратимом процессе сжатия к работе затраченной в действительном процессе сжатия компрессорной машины без учета механически потерь.

Для поршневых и роторных компрессоров с интенсивным охлаждением используют понятие изотермического относительного КПД:

Для компрессоров с неинтенсивным охлаждением используют понятие адиабатного относительного КПД:

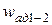
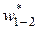
Наиболее универсальным является внутренний относительный КПД, учитывающий все внутренние потери компрессорной машины, кроме механических потерь, связанных с утечками газа через уплотнения и представляет собой отношение работы в обратимом процессе сжатия к действительной эффективной работе во внешнеадиабатном процессе , т.е. таком при котором теплообмен через корпус компрессора отсутствует:

— коэффициент необратимых превращений работы в теплоту.

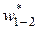
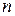
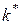
Действительная эффективная работа во внешнеадиабатного процессе определится путем замены показателя политропы показателем внешнеадиабатного процесса :

Если пренебречь изменением скорости газа в процессе сжатия и потерями теплоты через корпус компрессора то получим политропный КПД:

Политропный КПД позволяет оценить совершенство компрессорных машин без определения объемной доли или массовой подачи газа, используя только значения термодинамических параметров, которые изменяются в процессе сжатия и значения показателя адиабаты в диапазоне изменений указанных параметров.

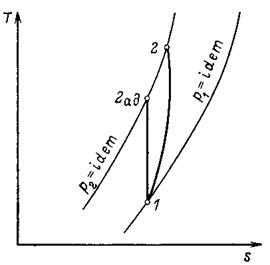
На Рис. 6.5 приведен обратимый адиабатный и действительный процессы сжатия в Т-S координатах.

Рис. 6.5. Обратимый адиабатный и действительный процессы сжатия в Т-S координатах

Как видно расчетное значение температуры действительного процесса сжатия выше, чем в конце адиабатного сжатия. Вводя для реальных газов фактор сжимаемости 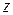работа затраченная в компрессоре на сжатие определится:

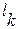
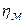
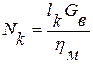
Мощность, затрачиваемая на привод компрессора, определяется удельной работой и секундным расходом газа с учетом механических потерь (потери на трение рабочих элементов об газ, трение в подшипниках и редукторе привода компрессора) выраженных через механическое КПД :

.

7. Циклы поршневых двигателей внутреннего сгорания и газотурбинных установок. Основные допущения и принципы расчёта; изображение циклов в рабочей и тепловой диаграммах. Анализ и сравнение различных групп циклов по основным параметрам.

Тепловые двигатели, в которых подвод теплоты к рабочему телу осуществляется в результате сгорания топлива внутри данного двигателя, называются двигателями внутреннего сгорания.

В таких двигателях топливо сгорает в цилиндре или в камере сгорания, а рабочим телом являются неконденсирующиеся газы – воздух, продукты сгорания. Причем на первом этапе рабочее тело – воздух или смесь воздуха с парами топлива, а на втором этапе – газообразные продукты сгорания топлива. Так как на всех стадиях цикла рабочее тело находится в газообразном состоянии, то циклы принято называть тепловыми газовыми циклами.

Двигатели с газообразным рабочим телом разделяют на три группы:

Источник

Оптимизация режимов работы газоперекачивающих агрегатов с газотурбинным приводом по условию максимального КПД

Одной из наиболее важных задач в условиях использования газотурбинного энергопривода на газопроводах является задача обеспечения наиболее экономичных режимов работы ГПА при перекачке заданного количества газа, что всегда связано с экономией топливного газа по станции.

n = n₀ , (5.23)

Изменение частоты вращения вала нагнетателя (Рис. 5.14) осуществляется до величины 3250 с интервалом между рассматриваемыми характеристиками 250 об./мин. и весьма наглядно показывает как изменяется относительный КПД нагнетателя при изменении подачи газа и частоты вращения его вала.

Естественно, что при рассмотрении характеристики нагнетателя в достаточно широком диапазоне изменения частоты вращения его вала, необходимо выдерживать условие работы нагнетателя в допустимой зоне работы, n_min £ n £ n_max. [16].

Рассмотрение данных Рис. 5.14 показывает, что значительный перерасход топливного газа на величину 3-6 % связан с характером зависимости h_пол. = f (Q_пр.), характеризующей резкое падение КПД нагнетателя по краям этой характеристики.

Для достижения максимального политропного КПД нагнетателя необходимо выдерживать оптимальные режимные значения e, Q и n, соответствующие h_пол. = max, которые не всегда соответствуют оптимальным значениям по этой зависимости (Рис. 5. 14) и что связано с несогласованностью характеристик нагнетателя и газопровода.

Результаты эксплуатационных данных показывают, между изменением в расходе топливного газа по ГПА и политропгым КПД нагнетателя существует следующая простая зависимость [14]:

Полученное соотношение показывает, насколько важно в условиях эксплуатации обеспечить условие работы нагнетателей на режимах h_пол. = max. Уравнение (5.24) показывает, что снижение численного значения КПД нагнетателя только на 1% приводит к перерасходу топливного газа на 1,1%.

Выбор оптимальной частоты вращения вала нагнетателя, осуществляемый по условию h_пол. = max. в практических условиях может быть проведен по предварительному определению диапазона изменения подачи газа по нагнетателю по его характеристике в зоне наивысшего значения КПД нагнетателя.

Соответственно может быть определено и соотношение давлений сжатия по первому нагнетателю (в условиях двухступенчатого сжатия) по условию h_пол. = max. [16]:

(5.25)

Второй последовательно работающий в группе агрегат также должен работать при максимальном значении политропного КПД. Его объемная производительность в этом случае будет определяться соотношением:

Q₂ = Q₁ (5.26)

Оптимальная частота вращения для этой производительности, а также соотношение давлений сжатия определяются по следующим соотношениям:

(5.27)

(5.28)

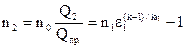
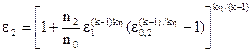
При использовании полнонапорных нагнетателей в качестве расчетного уравнения используется практически только уравнение (5.25).

С учетом приведенных соотношений, оптимальная зона работы нагнетателя типа 370-18-1 по условию максимального КПД ГТУ будет характеризоваться данными Рис. 5.15.

Значительный интерес всегда представляет совмещение характеристик нагнетателя и ГТУ с целью оценки совпадения значений их максимальных КПД. Решение этой задачи начинается прежде всего с определения мощности, потребляемой нагнетателем, при которой выполняется условие h_пол. = max.

Определение мощности, потребляемой нагнетателем, можно осуществить с использованием известных формул приведения (для двухступенчатого сжатия):

(5.29)

(5.30)

При использовании полнонапорных нагнетателей расчетные соотношения несколько упрощаются и для определения мощности можно использовать только соотношение (5.29).

Переход к характеристикам газотурбинной установки осуществляется по условию равенства мощностей нагнетателя и ГТУ, N_е,ГТУ = N_i,наг. + N_мех., где N_мех. – механические потери мощности в системе соединения турбины и нагнетателя.

Зависимость эффективного КПД ГТУ от ее мощности определяется соотношением:

; (5.31)

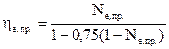
Результаты совмещения характеристик нагнетателя и газовой турбины с учетом соотношений (5.2 и 5.25-5.31) приведены на Рис. 5.16.

Приведенная номограмма совмещения оптимальных режимов работы ГПА по условиям максимального значения КПД нагнетателя и ГТУ дает возможность при заданной производительности нагнетателя в первом приближении определять и оптимальную температуру газов перед турбиной высокого давления, при которой КПД также будет иметь максимальное значение.

Приведенная относительная мощность установки от приведенной температуры газов перед газовой турбиной в первом приближении определяется соотношением [6]:

В условиях, когда температуру газов перед ТВД определить сложно, ее можно определить расчетным путем по известной температуре газов за ТНД.

Следует отметить, что аналогичным образом могут быть построены номограммы и для других типов ГПА с другими нагнетателями и другими типами газотурбинных установок.

Приведенная относительная температура газов за ТНД в зависимости от приведенной мощности установки в первом приближении может быть определена по соотношению:

Наличие уравнений (5.32) и (5.33) позволяет легко построить графические зависимости между переменными, входящими в эти соотношения для различных режимов работы и по ним судить как изменяются эти одни из основных параметров ГТУ в процессе эксплуатации.

Решение. Решение данной задачи осуществляется в следующей последовательности: вначале оценивается техническое состояние нагнетателя, затем определяется потребляемая им мощность и подача газа. Найденная величина мощности используется как для определения технического состояния газотурбинной установки, так и для определения расхода топливного газа и эффективного КПД самой ГТУ.

Средние значения температуры и давления в процессе сжатия:

Средняя изобарная теплоемкость любого природного газа в процессе сжатия может быть определена по следующему эмпирическому соотношению в зависимости от процентного содержания метана в газе и параметров процесса сжатия [ ], В данном примере ее можно принять равной С_pm = 2,17 кДж/кг 0 С.

Для определения реальной удельной работы сжатия газа в нагнетателе, его следует рассматривать как реальный газ, функции которого определяются в зависимости от двух переменных (например, P,t), с учетом коэффициента Джоля-Томпсона, характеризующим отличие реального газа от идеального.

Источник

Поэтому для получения больших давлений применяется ступенчатое сжатие газа с промежуточным охлаждением между ступенями во внешних теплообменниках водой или атмосферным воздухом.

Увеличение числа ступеней повышает экономичность процесса сжатия.

4.7. Коэффициенты полезного действия нагнетателей

Для оценки эффективности сжатия в нагнетателях пользуются, чаще всего, понятием относительных КПД, т. е. отношение работы, затраченным в идеальном процессе l_ин сжатия, к работе действительного l_k процесса.

Изотермическим КПД называется выражение (при Т = const)

. (4.25)

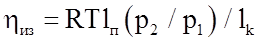
Для нагнетателей без теплообмена с внешней средой идеальная работа сжатия определяется из уравнения изоэнтропического процесс, а КПД называют изоэнтропическим (адиабатным) или для нагнетателей объемного типа – индикаторным в форме:

. (4.26)

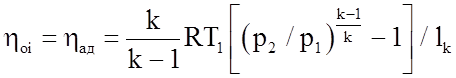
Более удобно формулу (4.26) для оценки КПД после испытаний можно представить в виде:

. (4.27)

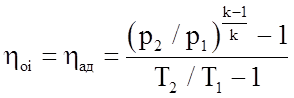
Формулы (4.25) – (4.27) дают типичное решение только для идеального газа (и в охлаждаемых компрессорах). В практической деятельности пользуются выражением для политропного КПД в виде:

. (4.28)

, (4.29)

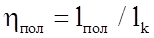
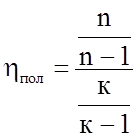
где n = const, показатель политропы сжатия.

Можно выявить связь между η_ад и η_пол из следующего выражения:

. (4.30)

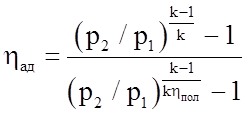
Из (4.29) следует, что с увеличением соотношения р₂/р₁ растет разница между η_пол и η_ад.

Общий КПД компрессора выражается через КПД отдельных ступеней.

Более строго выражение для КПД можно получить из уравнения энергетического баланса компрессора (с использованием e-h диаграммы).

4.8. Принцип действия радиальной ступени нагнетателя

В состав ступени нагнетателя входят6 рабочее колесо, диффузор, входные и выходные участки (патрубки или отводы). Тогда многоступенчатый нагнетатель будет состоять из нескольких последовательно соединенных ступеней.

В ступени центробежного нагнетателя рабочее тело поступает через входной кольцевой участок между валом и входным патрубком в рабочее колесо, где после изменения направления от осевого на радиальное попадает в каналы, образованные основным и покровным дисками и рабочими лопатками.

Движение рабочего тела в межлопаточных каналах рабочего колеса сложное, состоящее из переносного (скорость u) и относительного (скорость w), в совокупности составляющих абсолютное движение (скорость с). Связь между скоростями для конкретных углов характеризуется соответственно входным и выходным треугольниками скоростей.

В каналах колеса рабочему телу предается энергия от стенок результатом чего является повышение его кинетической энергии в абсолютном движении (скорость с растет и с₂ > с₁).

Чаще всего сочетание канала от входа к выходу несколько увеличивается, относительная скорость падает, что приводит к росту статистического давления в рабочем канале. Значительное увеличение сечения и уменьшение скорости W приводит, однако, к потерям. Поэтому форма канала должна изменяться так, чтобы соблюдалось соотношение W₁≈ W₂.

Изменение окружной скорости от U₁ до U₂ (на радиусах r₁ и r₂) вызывают дополнительное повышение давления вследствие действия центробежных сил.

После выхода из рабочего колеса рабочее тело попадает в диффузор, где поток тормозится, а давление повышается.

На рис. 4.14 показаны изменения, Т, р, u, c, и w для сечений ступени нагнетателя. Принято, что в зазоре между выходом из рабочего колеса и входом в диффузор изменение параметров не происходит.

Осевой нагнетатель конструктивно сходен с турбиной осевого типа (его называют обращенной турбиной). Ступень осевого нагнетателя приведена на рис. 4.15.

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Понятие о внутреннем КПД турбокомпрессоров

Внутренний КПД турбокомпрессоров служит для оценки совершенства проточной части и качества преобразования энергии в ней.

В общем случае под КПД понимают отношения полезной работы к подведенной (затрачиваемой):

. (2.32)

В зависимости от того, что понимается под полезной и затраченной работами, получают различные виды КПД. В качестве затраченной работы в выражениях для внутреннего КПД всегда фигурирует внутренний напор h_i. Ниже приведена классификация различных видов внутреннего КПД.

Численные значения напоров (работ), которые входят в выражения для КПД могут быть определены через соответствующие площади на Т-S диаграмме.

Классификация коэффициентов полезного действия

Внутренний КПД
По учету изменения кинетической энергии
По полным параметрам	По статическим параметрам
По виду полезной работы
Политропный hп	Адиабатный hад	Изотермный hиз

В соответствие с уравнением Бернулли

.

Произведем сравнение различных КПД по виду полезного напора.

1. Политропный КПД выражается соотношением:

. (2.33)

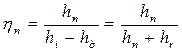
Политропный напор из формулы (2.29)

,

что соответствует пл. 122¢¢¢351 (рис. 2.8).

Затраченная работа (внутренний напор) без учета изменения кинетической энергии

,

произведя замену (нужно помнить, что для совершенного газа и ), получим

.

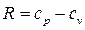
Подставим выражения для полезной и затраченной работ в формулу (2.33)

. (2.34)

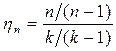
Потеря напора на трение h_r в T-S диаграмме пропорциональна площади пл. 12651. Таким образом, политропный КПД на T-S диаграмме представляет собой отношение площадей:

.

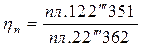
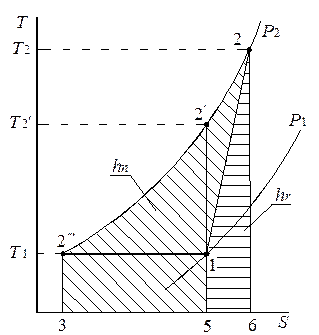Рис. 2.8. К определению политропного и адиабатного КПД

2. Адиабатный КПД определяетсяпо формуле

. (2.35)

Затраченная работа в адиабатном КПД такая же, как и в выражении для политропного КПД, а полезная работа (адиабатный напор) описывается формулой (2.30), тогда

, (2.36)

Через площади на T-S диаграмме

.

Из-за того, что в полезный напор политропного КПД в компрессоре входит дополнительная работа Δl (пл.122¢1), политропный КПД выше адиабатного ( ). Главное достоинство η_ад заключается в том, что его легко рассчитать, т.к. не нужно знать показатель политропы. Адиабатный и политропный КПД применяются для оценки качества преобразования энергии неохлаждаемых компрессоров, секций и ступеней.

Изотермный КПД используется для охлаждаемых компрессоров и учитывает помимо потерь (включая потери в холодильниках) близость процесса сжатия к изотермическому:

. (2.37)

Полезная работа в изотермическом процессе h_из известна из формулы (2.31). Политропный напор, входящий в величину затраченной работы, рассчитывается по формуле (2.29), где показатель политропы n

Источник

Что такое политропный кпд

В прошлый раз я говорил про то, откуда берётся тепловая энергия для генерации электричества. А как эта тепловая энергия преобразуется? Почему КПД АЭС около 33%? Зачем электростанции вообще нужен конденсатор? Для ответов на эти вопросы мы должны переместиться в прошлое, и постепенно, слой за слоем, нарастить это знание.

Предыдущую статью из этого цикла Вы можете прочитать по ссылке: Как работает атомный энергоблок. Часть 1

Все слышали про первый закон термодинамики. По сути, он является конкретизацией закона сохранения энергии для тепловых двигателей. Этот закон гласит, что невозможно создание двигателя, который работал бы без получения энергии от внешнего источника. Также невозможно создание двигателя, который совершал бы больше работы, чем к нему подводилось бы энергии. Для нас это сейчас логично и понятно, и совершенно очевидно, что КПД не может превышать 100%.

Коэффициент полезного действия — это отношение энергии затраченной на совершение работы ко всей использованной энергии.

В случае с тепловыми машинами используется так называемый термический КПД. Его значение — теоретический предел для конкретного термодинамического цикла, не считая потерь от теплопередачи, трения и т.д.

Когда мы подводим тепло (тепловую энергию), не вся она переходит в работу. Для того, чтобы вернуть рабочее тело — вещество которое мы нагреваем чтобы раскрутить турбину — в начальное состояние, надо часть энергии у него забрать, охладить его. Соответственно, часть энергии нагрева уходит на повышение температуры внешней среды.

В виде формулы это будет записано следующим образом:

Где Q₁ это подведённая теплота, Q₂ отведённая, соответственно Q₁-Q₂ это работа, которую совершило рабочее тело.

Но какой максимум мы можем выжать из тепла для совершения работы? Этим вопросом задался не кто иной как Сади Карно.

Вопрос звучал примерно так: «А почему паровоз жрёт так много и производит так мало, может у нас плохой двигатель? Или конструкция не очень?». Резонно, и многие хотели бы иметь такую систему, которую можно греть, а всё затраченное тепло тратить на работу и ехать, рассекая пространство. КПД такого двигателя мог бы достигать 100%! Но, как оказалось, такое в природе невозможно.

Давайте задумаемся вот над чем. Представим, что у нас на столе стоит чашка горячего чая. Постепенно она остывает, и это происходит неизбежно. В чем причина? Дело в том, что тепло произвольно переходит только от более горячего тела к более холодному, и никак иначе. При отсутствии разницы температур тепло рабочего тела не может быть преобразовано в работу, отсутствует поток теплоты. Это было установлено эмпирически на основе опыта. Поскольку в реальной жизни недостижима температура равная абсолютному нулю, то и КПД теплового цикла не может составлять 100%.

Чтобы показать, как это выглядит в жизни, посмотрим на следующую иллюстрацию:

Тепловой двигатель и вечный двигатель второго рода

Вечный двигатель второго рода не нарушает первого закона термодинамики, энергия не берется из ниоткуда. Но такой двигатель невозможен, ведь нет стока для теплоты. Невозможность такого цикличного процесса объясняет требование наличия конденсатора в любой тепловой системе. Получается, что для работающего цикла нам нужны минимум 4 составляющие:

С этим разобрались, а теперь давайте вернёмся к КПД. Какова максимальная эффективность цикла? И чем она обусловлена?

На оба этих вопроса и ответил Карно. Максимальная эффективность обусловлена только температурами горячего и холодного источников, не зависит от рабочего тела, не зависит от конструкции двигателя. В итоге, второй закон термодинамики приводит нас к следующему определению максимального КПД цикла (или КПД цикла Карно):

Где T₁ – температура источника тепла, T₂ – температура холодильника (стока).

Этот КПД является предельным для заданной разницы температур. То есть, можно увеличить его подняв температуру горячего источника, либо снизив температуру холодного. Естественно, что температура не может быть бесконечно большой или бесконечно маленькой. Так что в существующих реалиях мы вынуждены прибегать к температуре окружающей среды в качестве стока, и к допустимым температурам для оборудования в качестве источника. Для каждого циклического процесса наибольшая температура подбирается так, чтобы можно было выжать максимум из топлива, и при этом система справилась бы с отводом теплоты.

Как увеличить КПД АЭС?

Цикл Карно представляет из себя замкнутую систему из двух адиабатных (1-2, 3-4) и двух изотермических (2-3, 4-1) процессов.

Краткий экскурс в процессы происходящие с рабочим телом

Все процессы являются частными случаями политропного процесса. Я нашёл отличную табличку в интернете для пояснения (Физика в таблицах и формулах, Трофимова Т. И., 2002 г., стр. 94)

Цикл Карно является идеальным, это модель, в которой отсутствуют такие понятия как трение, потери при расширении рабочего тела, потери давления при движении рабочего тела, и так далее. Рабочих циклов существует великое множество. Это и циклы для двигателей внутреннего сгорания (цикл Дизеля, цикл Отто, например), циклы для двигателей внешнего сгорания (см. двигатель Стирлинга — кстати, такой можно заказать за приемлемую цену на АлиЭкспресс, он даже от чашки чая работать будет).

Первый закон термодинамики говорит о количественной составляющей теплового цикла. Второй говорит о качественной. А вот увидеть на диаграмме давления и объема потери в реальном цикле не так просто. Но этот вопрос решаем.

Внимание! Дальше частичка неизбежного матана!

Итак, если мы проанализируем соотношение изменения теплоты при изотермическом расширении, рассмотрев цикл Карно как сумму бесконечно малых циклов, то получим новую величину, которая известна как термодинамическая энтропия.

Что это такое? Энтропия (S) — это мера беспорядочности движения частиц вещества. Иными словами, очень приближённо можно назвать энтропию мерой качества процессов. При подводе теплоты энтропия всегда растёт в равной или в большей степени, чем отношение подведённого тепла к температуре. Это означает, что часть тепла всегда рассеивается без совершения работы. Логично, что при идеальном адиабатном процессе энтропия не изменяется. Для цикла, как очевидно, изменение энтропии всегда нулевое, потому что рабочее тело каждый раз перед началом следующего цикла возвращается в исходное состояние, со своим исходным значением энтропии.

Откуда взялись реальные термодинамические циклы?

Чем выше энтропия – тем ближе система к термодинамическому равновесию. На рисунках циклов выше точки являются координатами различных состояний рабочего тела. Чем больше тепла в системе – тем больше значение энтропии. Чем больше тепла мы отвели — тем меньше энтропия. Вне цикла энтропия достигла бы своего максимального значения и система пришла бы в равновесие.

Каждому состоянию вещества (каждой точке на диаграммах) соответствуют определённые значения термодинамических параметров. По двум из них можно определить все остальные. Энтропия является как раз таким параметром, в дополнение к давлению, температуре и объему. Это то, что нам нужно! Вперёд, строить новые диаграммы!

Вот так будет теперь выглядеть цикл Карно на диаграмме T-S, то есть такой, где каждое состояние вещества можно наглядно показать с помощью значений температуры и энтропии:

Цикл Карно, в данном представлении — это обычный прямоугольник

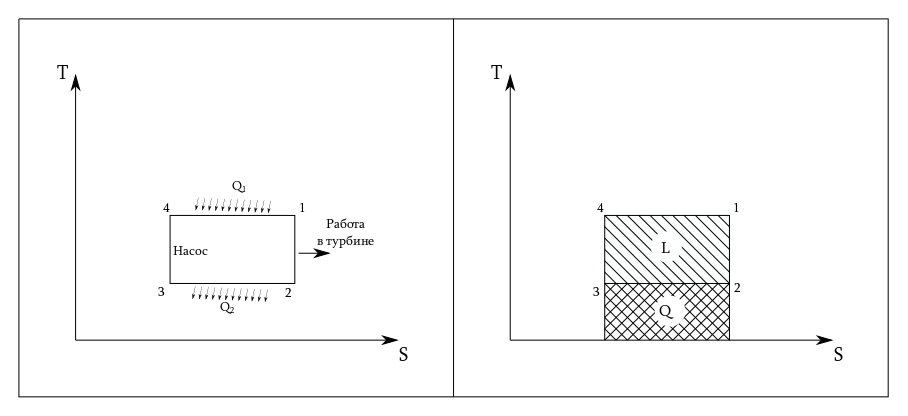
Площадь фигуры 1-2-3-4 равна работе, которую совершило рабочее тело, площадь прямоугольника под процессами 2-3 это тепло отданное в конденсаторе. Значит КПД — это отношение площадей этих фигур. В реальном процессе часть энергии уйдет на увеличение энтропии (трение, расширение, процессы быстрые, много причин), и с помощью T-S диаграммы можно наглядно это показать. Затраченная теплота увеличится, работа останется почти на том же уровне, а КПД уменьшится — смотрите на площади фигур. Обратите внимание на точки с индексом r — это реальные точки, с ними мы имеем дело в реальной жизни.

Цикл Карно с учетом потерь и рассеяния тепла

Установки в тепловой энергетике бывают паротурбинными (в качестве рабочего тела выступает испаряющаяся жидкость, например — вода) и газотурбинными (в качестве рабочего тела некий газ; см. Цикл Брайтона). Разница будет в наличии фазового перехода. Опуская многие подробности, скажу лишь, что рассматриваются два агрегатных состояния вещества, в них включена также и переходная область между перегретым паром и жидкостью. Вот так это выглядит:

Внутренняя часть «купола», изображённого на картинке, это область фазового перехода между жидким и газообразным состоянием. Зелёная линия – это линия кипящей жидкости, фиолетовая – линия сухого насыщенного пара (в паре не остаётся влаги если эту линию переступить). Как можно заметить, при определённом давлении p₃ вода не имеет фазового перехода, то есть нет стадии перехода жидкости в газ. При параметрах, превышающих критические давление и температуру, уже отсутствует понятие пара, это закритическая жидкость. Для воды критическое давление и температура это 22.064 МПа и 373.95 °C (в абсолютных единицах 647.1 Кельвин). При фазовом переходе из жидкости в газ температура не изменяется при подведении тепла. Это связано с тем, что энергия, передаваемая рабочему телу, расходуется не на повышение температуры, а на разрыв связей в жидкости.

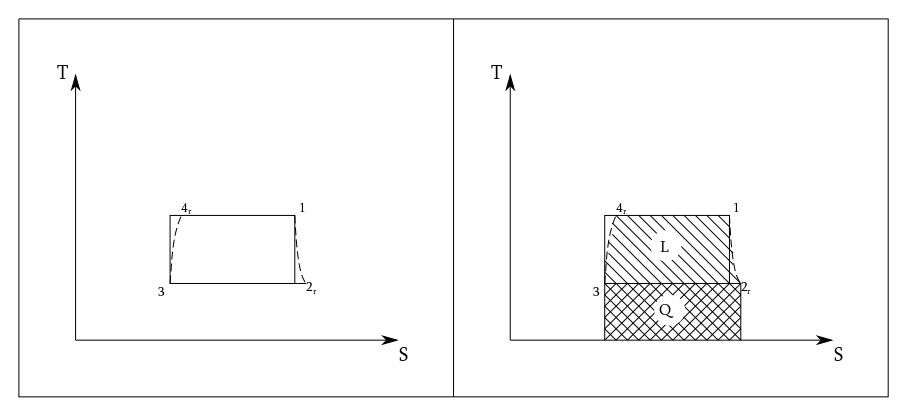
А давайте теперь посмотрим, как будет выглядеть цикл Карно в случае двухфазной среды:

Замечательно, но точка 3 находится в области влажного пара, а значит, чтобы перекачать весь этот объём на участке 3-4r нам потребуется большой мощный компрессор, потери в котором будут существенными. Для того, чтобы этого избежать, сконденсируем пар до состояния жидкой воды, то есть получим состояние вещества на зелёной линии. Тогда вместо компрессора мы сможем использовать относительно миниатюрный конденсатный насос.

Вот с этим уже можно работать, правда есть один существенный нюанс:точка 2r находится в области влажного пара, а это не очень хорошо для турбины. Дело в том, что скорость пара в турбине составляет несколько сотен метров в секунду. Во влажном паре содержатся капельки жидкости, которые на большой скорости повреждают лопатки турбины. Такая турбина долго не проработает, поэтому нам нужно снизить влажность пара, чтобы он не разбомбил вращающиеся лопатки. Один из способов – это перегрев пара, и разделение турбины на часть с высоким давлением и часть с низким. Максимальное содержание влажной фазы обычно не превышает 15%.

Уже лучше. Таким образом мы и среднюю температуру подняли, что положительно скажется на КПД АЭС, и тепло лучше использовали. Но из этого цикла можно выжать ещё больше, если часть тепла возвращать в его более низкотемпературные части. Этот приём называется регенерацией теплоты. То есть, из тех участков, где мы уже выжали из рабочего тела максимум, мы можем частично возвращать тепло в цикл. Это позволит меньше греть воду в парогенераторе и повысить эффективность преобразования тепла в работу.

Помимо этого, между частями высокого и низкого давления можно использовать сепаратор, отделяющий влагу от влажного пара, а также сепарировать пар в ступенях турбины между лопатками. Всё это повышает эффективность работы паротурбинной установки, но эффективность ещё очень далека до КПД цикла Карно. Из-за естественных потерь в турбине и насосах КПД АЭС редко превышает 34%.

На десерт. Тут внесены все упомянутые изменения.
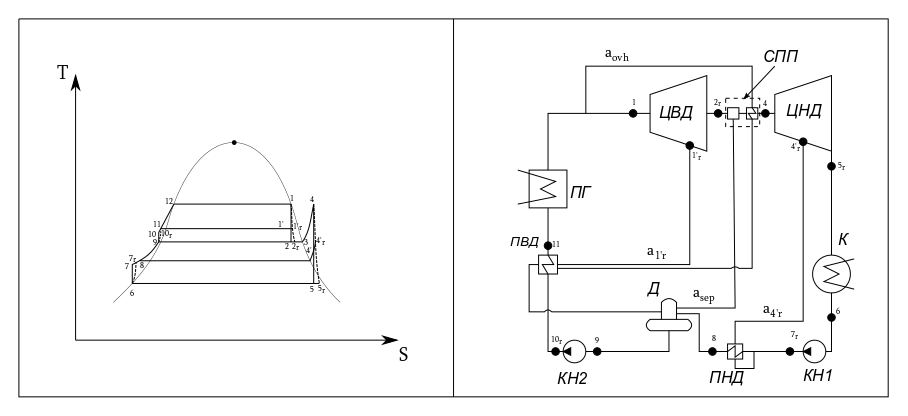
Сможете разобраться что к чему?

Внимательный читатель спросит,- А почему бы сразу не перегреть пар до входа в турбину? Дело в том, что на водо-водяных реакторах этот приём не будет эффективным. Нужно будет либо снизить давление на входе в турбину, либо ещё повысить параметры воды в первом контуре (исследования на эту тему ведутся, но по последним новостям зашли в тупик). Параметры на современных АЭС выбраны оптимальными с точки зрения безопасности, тепловой экономичности и конструкционных пределов. В реальности с перегретым паром работают только энергоблоки с жидкометаллическим теплоносителем, которые могут позволить себе перегрев пара до входа в турбину.

Неужели КПД АЭС настолько важен?

Зачем нужны эти ухищрения и высокая эффективность? Почему ради каких-то десятых долей процента создаются целые проектные институты и собираются огромные команды специалистов? Всё дело в том, что каждая малая доля прироста КПД АЭС– это прирост в выработке при тех же затратах тепла. Эти цифры кажутся ничтожными, поэтому давайте пересчитаем это в деньги.

Допустим, есть две реакторные установки, у одной КПД 33%, а у другой 33.1%. То есть имея 3200 МВт тепла первая установка даст 1056 МВт электрической мощности, а вторая 1059.2 МВт. Разница составляет 3.2 МВт. Сколько это в рублях?

Цена отпускаемого кВт-ч для АЭС примерно 2 рубля. Считаем сколько это принесёт станции за год. 3200*365*24*2= 56064000 р. То есть с выигрышем всего на 0.1% КПД вторая станция за год заработает больше на 56 миллионов при том же тепловыделении в реакторе!

Тут я вынужден остановиться и предоставить пытливым читателям возможность самостоятельно ознакомиться со способами дальнейшего увеличения эффективности циклов и глубже погрузиться в мир технической термодинамики. В будущем мы обсудим вопросы передачи теплоты и выясним, почему очень высокая температура — это плохо, даже если материалы могут её выдерживать.

Также вы можете прочитать статью о тепловой солнечной энергетике:

Другие мои статьи и заметки вы можете читать:
В группе нашего коллектива ВКонтакте, под хэштегом #Вододохов@century_arch

Также, чтобы не пропускать новые статьи, советую подписаться на нашу рассылку в Телеграм:

Над статьёй работали:

Автор: Н.С. Вододохов
Редакторы: И.А. Нестеров, К.А. Овчинников

Изображения взяты из открытых источников и использованы в образовательных целях.

Источник