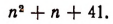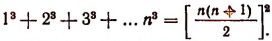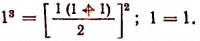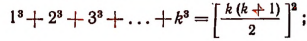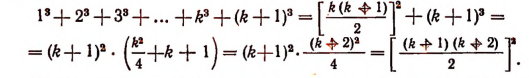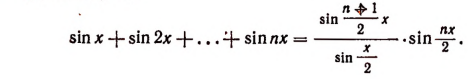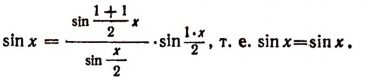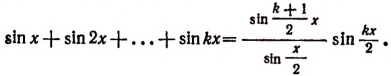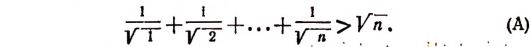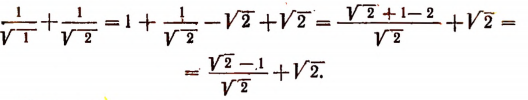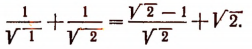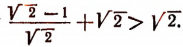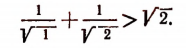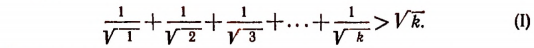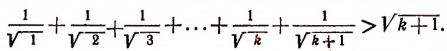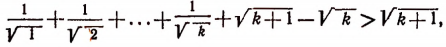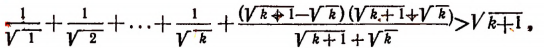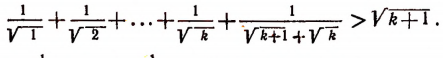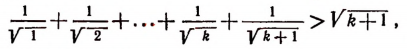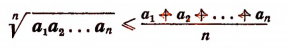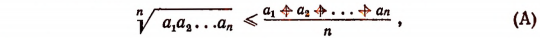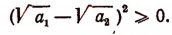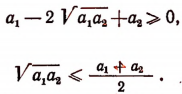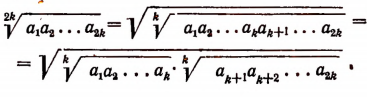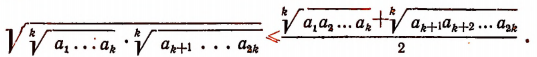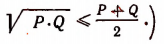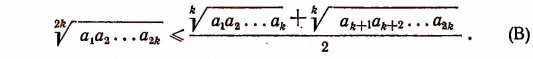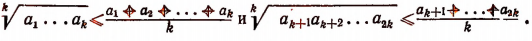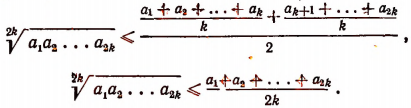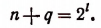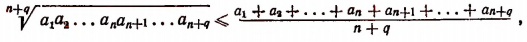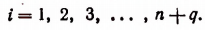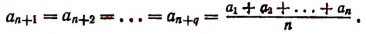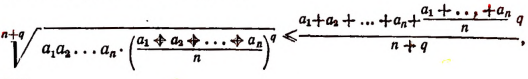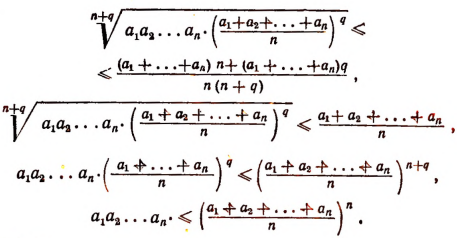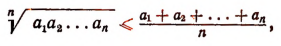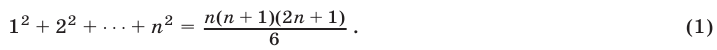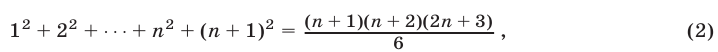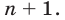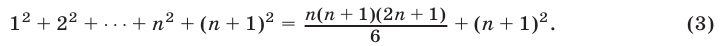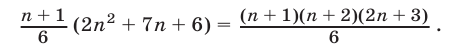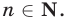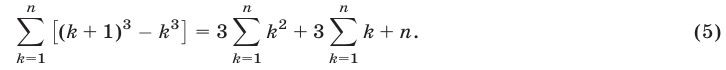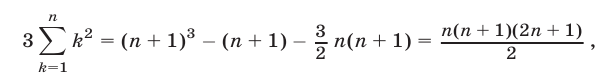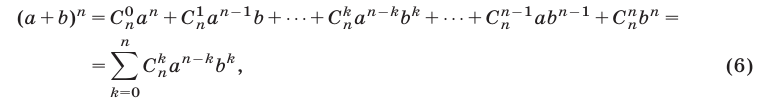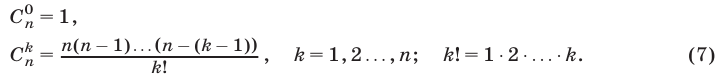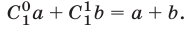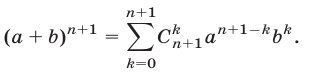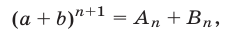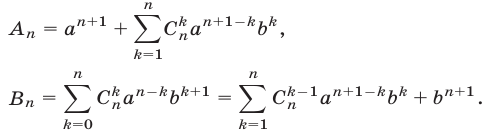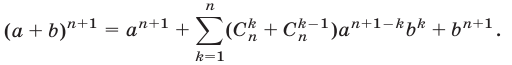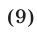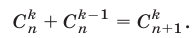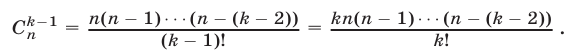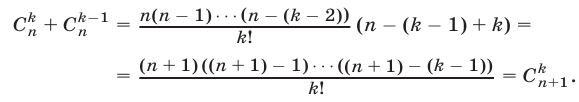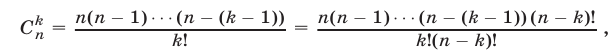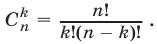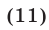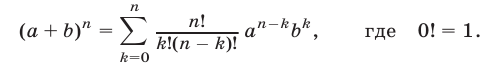Что такое полная математическая индукция приведите пример
Метод математической индукции для чайников
Метод полного перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией. Этот метод имеет крайне ограниченную область применения в математике, так как обычно математические утверждения касаются бесконечного множества объектов (например, натуральных чисел, простых чисел, квадратов и т.п.) и перебрать их невозможно.
Основы метода математической индукции
Доказательство с помощью метода математической индукции проводится в два этапа:
Метод математической индукции применяется в разных типах задач:
Ниже вы найдете примеры решения задач, иллюстрирующие применение метода математической индукции, а также ссылки на полезные сайты и учебник и небольшой видеоурок по ММИ.
Математическая индукция: задачи и решения
Доказательство кратности и делимости
$$a_n = 2n^3+3n^2+7n, \quad b=6.$$
Доказательство равенств и неравенств
Задача 5. Доказать равенство
Задача 6. Доказать методом математической индукции:
Задача 7. Доказать неравенство:
Задача 8. Доказать утверждение методом математической индукции:
Задача 9. Доказать неравенство:
Вычисление сумм
Задача 11. Доказать методом математической индукции:
Задача 12. Найдите сумму
Заказать решение
Полезные ссылки о ММИ
Кратенький видеоурок о ММИ
Математическая индукция
Математическая индукция — один из методов математического доказательства, используется чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что, если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку (в этом заключается индукционный переход). Тогда, если мы толкнём первую косточку (это база индукции), то все косточки в ряду упадут.
Содержание
Формулировка
Предположим, что требуется установить справедливость бесконечной последовательности утверждений, занумерованных натуральными числами: 
Тогда все утверждения нашей последовательности верны.
Логическим основанием для этого метода доказательства служит так называемая аксиома индукции, пятая из аксиом Пеано, определяющих натуральные числа. Верность метода индукции эквивалентна тому, что в любом непустом подмножестве натуральных чисел существует минимальный элемент.
Принцип полной математической индукции
Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть имеется последовательность утверждений 











В этой вариации база индукции оказывается излишней, поскольку является тривиальным частным случаем индукционного перехода. Действительно, при 


Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.
История
Примеры
Задача. Доказать, что, каковы бы ни были натуральное n и вещественное q ≠ 1, выполняется равенство
Доказательство. Индукция по n.
Переход: предположим, что

что и требовалось доказать.
Комментарий: верность утверждения 
Вариации и обобщения
Примечания
Литература
Ссылки
Полезное
Смотреть что такое «Математическая индукция» в других словарях:
МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — полная математическая индукция (наз. в математике часто просто полной индукцией; в этом случае это понятие следует отличать от рассматриваемого в нематематич. формальной логике понятия полной индукции), – прием доказательства общих предложений в… … Философская энциклопедия
МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — МАТЕМАТИЧЕСКАЯ индукция, способ доказательства или определения некоторого свойства A для всех n случаев, основанный на переходе заключения о наличии свойства A от n к n+1. Математическая индукция состоит из двух этапов: установление A для… … Современная энциклопедия
МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — общий способ математического доказательства или определения некоторого свойства А для всех натуральных n, основанный на заключении от n к n+1. Математическая индукция состоит из двух этапов: а) установление А для некоторого начального n0; б)… … Большой Энциклопедический словарь
Математическая индукция — МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ, способ доказательства или определения некоторого свойства A для всех n случаев, основанный на переходе заключения о наличии свойства A от n к n+1. Математическая индукция состоит из двух этапов: установление A для… … Иллюстрированный энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ, метод, доказывающий, что математическое утверждение верно для любого положительного целого числа п, если выполняются два условия: 1) оно верно для основной величины, например, 1, и 2) если оно верно для значения k, то… … Научно-технический энциклопедический словарь
математическая индукция — общий способ математического доказательства или определения некоторого свойства А для всех натуральных n, основанный на заключении от n к n + 1, математическая индукция состоит из двух этапов: а) установление А для некоторого начального n0;… … Энциклопедический словарь
МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — метод доказательства математич. утверждений, основанный на принципе математической индукции: утверждение (х), зависящее от натурального параметра х, считается доказанным, если доказано А(1) и для любого натурального пиз предположения, что верно… … Математическая энциклопедия
Математическая индукция — весьма общий способ математических доказательств и определений. Индуктивные доказательства основаны на так называемом принципе М. и., являющемся одной из основных математических аксиом. Пусть, например, требуется доказать для любого… … Большая советская энциклопедия
МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ — общий спо соб матем. доказательства или определения нек рого свойства А для всех натуральных п, основанный на заключении от п к n +1, М. и. состоит из двух этапов: а) установление А для нек рого начального no; б) обоснование перехода от n к п + 1 … Естествознание. Энциклопедический словарь
Индукция Математическая, Полная Математическая Индукция — а средство доказательства общих положений в матемантике и др. дедуктивных науках. Этот прием опирается на использованние двух суждений. Первое представляет собой единичное суждение и наз. базой индукции. В нем доказывается, что 1 обладает… … Словарь терминов логики
Математическая индукция в математике с примерами решения и образцами выполнения
Дедукцией называется переход от общего утверждения к частному. Приведем пример.
Площадь всякого треугольника равна
это утверждение общее.
От этого общего утверждения можно сделать переход к частному утверждению, например такому:
площадь равностороннего треугольника равна
т. е. равна 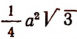
Дедукция есть одна из форм умозаключения. (Дедукция происходит от латинского слова «deductio» — выведение.)
Индукцией называется переход от частного утверждения к общему. Индукция есть также одна из форм умозаключения, применяя которую от знания отдельного факта идут к обобщению, к общему положению. (Индукция происходит от латинского слова «inductio» — наведение, побуждение.)
Все формы умозаключения связаны между собой, а потому связаны между собой дедукция и индукция. Одна дедукция (или одна индукция) никогда не может обеспечить познания объективной действительности.
Легкомысленное применение индукции может привести к неправильным выводам. Приведем пример.
Подставив в это выражение вместо п нуль, получим простое число 41. Подставив вместо п единицу, получим 43, т. е. опять простое число. Продолжая подставлять вместо п последовательно 2; 3; 4; 5; 6; 7; 8; 9; 10; 11, получим соответственно 47, 53; 61; 71; 83; 97; 113; 131 151; 173, т. е. опять же числа простые. Можем ли мы теперь быть уверенными в справедливости такого утверждения:
«Выражение 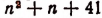
Быть уверенными в справедливости этого утверждения мы не можем, так как полученные выше результаты не являются достаточным основанием для такого утверждения. Они являются лишь основанием для предположения о верности этого утверждения. В действительности более полное исследование выражения 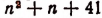
Этот пример показывает, что утверждение может быть верным при одних значениях натурального числа п и неверным при других.
Математическая индукция есть весьма общий метод, позволяющий во многих случаях исследовать законность перехода от частного утверждения к утверждению общему.
Принцип математической индукции можно сформулировать следующим образом.
Теорема о математической индукции
Пусть S(n)—некоторое утверждение, в формулировку которого входнт натуральное число п. Пусть, во-первых, утверждение 
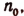
Доказательство:
Допустим, что утверждение S(n) не справедливо при некотором 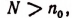
S(N —3) и т. д.
Таким образом (каким бы большим ни было число N), мы рано или поздно, отнимая от этого числа по единице, дойдем до числа 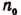

Приведенное доказательство теоремы о математической индукции может показаться некоторым читателям труднопонимаемым. Поэтому ниже приводится несколько упрощенная схема метода математической индукции.
Если в утверждении некоторой теоремы фигурирует целое положительное число п и если из справедливости этой теоремы для какого угодно частного значения п = k следует справедливость ее для значения k + 1, то, коль скоро это утверждение справедливо для п — 1, оно будет справедливо для любого целого положительного числа п.
Здесь дело обстоит так. Сначала мы убеждаемся в том, что теорема верна при п = 1. Затем, предполагая, что она верна для какого угодно частного значения п = k, доказываем ее справедливость для п = k + 1.
После этого рассуждаем так: поскольку теорема верна для п = 1, значит, она будет верной и для п — 1 + 1, т. е. для п = 2. Поскольку она верна для п = 2, она будет верной и для п = 2 + 1, т. е. для п = 3 и т. д.
Применение метода математической индукции
Примеры:
1. Доказать, что
Этой формулой утверждается следующее: для того чтобы найти сумму кубов нескольких первых натуральных чисел, надо последнее из них умножить на число, большее его на единицу, полученное произведение разделить на 2 и возвести в квадрат.
Доказательство:
1. При п = 1 утверждение справедливо,
так как
2. Допустим, что утверждение справедливо при п = k, т. е
Утверждение оказалось верным и для п =k+1. Следовательно, теорема верна при всяком целом положительном значении п.
Доказательство:
1. При п = 1 утверждение справедливо, так как
2. Допустим, что утверждение справедливо при п = k, т. е.
Утверждение оказалось верным и для п = k + 1. Следовательно, формула верна при всяком целом положительном значении п.
3. Доказать, что при п > 1
Доказательство:
При п = 2 утверждение справедливо.
Действительно,
Итак, оказалось, что
Но 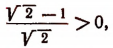
Докажем, что тогда будет справедливым и неравенство:
К обеим частям неравенства (I) прибавим по 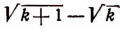
Но 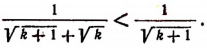
что и требовалось доказать,
Теперь мы видим, что утверждение (А) оказалось верным и для n=k+1. Следовательно, это утверждение справедливо при всяком целом положительном значении n, большем двух.
Существует очень много и других теорем, которые успешно доказываются с помощью метода математической индукции. Некоторые из таких теорем встретятся нам в последующих главах.
Доказательство неравенства
Иногда приходится применять метод математической индукции в несколько усложненной форме. Покажем это на примере. Пусть требуется доказать следующее неравенство:
где 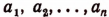
(Выражение 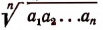
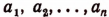

Во-первых, покажем справедливость неравенства (А) при n = 2.
Значит, при n = 2 неравенство (А) справедливо. Теперь докажем следующую лемму.
Лемма:
Если неравенство (А) верно при п = k, то оно будет верно при n=2k.
Доказательство:
Пользуясь свойствами арифметических корней, получим:
(Мы здесь воспользовались доказанным выше неравенством:
Поскольку мы предположили неравенство (А) верным при n = k, постольку
Учитывая эти два последних неравенства и неравенство (В), получим:
Итак, предполагая, что неравенство (А) справедливо при п = 2k, мы доказали, что оно будет справедливым и при п = 2k. Но ранее было доказано, что неравенство (А) справедливо при п = 2. Следовательно, оно будет справедливым и при п = 4,8,16, 32,…, т. е. при 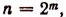
Теперь перейдем к доказательству неравенства (А) для любого натурального числа п.
Пусть п есть любое натуральное число. Если окажется, что п есть целая степень числа 2, то для такого п, как это уже было доказано, неравенство (А) справедливо. Если же п не есть целая степень числа 2, то к n всегда можно прибавить такое число q, что п+ q станет целой степенью числа 2. Итак, положим, что
Тогда получим неравенство:
справедливое при любых положительных 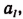
Это следует из того, что число п + q есть целая степень числа 2. Положим, что
Тогда получим последовательно:
что и требовалось доказать.
Значит, неравенство (А) справедливо при всяком натуральном п.
Метод математической индукции
Метод доказательства, называемый методом математической индукции, основан на следующем принципе, который является одной из аксиом арифметики натуральных чисел.
Предложение 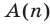
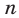
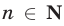
а) предложение 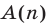
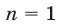
б) из предположения, что 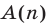
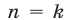
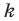
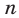
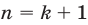
Этот принцип называется принципом математической индукции.
Под методом математической индукции понимают следующий способ доказательства: во-первых, проверяют истинность высказывания 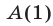
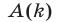
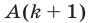
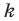
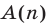
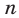
Пример:
Методом математической индукции доказать равенство
Доказательство:
При 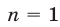
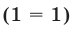
полученного из (1) заменой 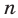
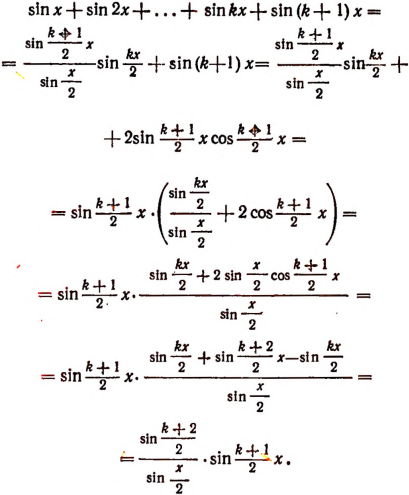
Прибавляя к обеим частям (1) слагаемое 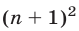
Преобразуя правую часть (3), получаем
Таким образом, равенство (2) является верным, и поэтому формула (1) доказана для любого
Дадим другое доказательство формулы (1), используя символ 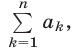
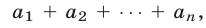
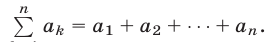
Полагая в (4) 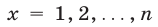
Левая часть (5) равна 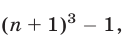
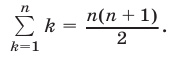
откуда следует равенство (1).
Пример:
Доказать, что для любых 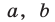
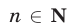
Правую часть формулы (6) называют разложением бинома, числа 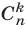
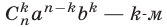
Доказательство. Воспользуемся методом математической индукции. При 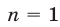
Предполагая справедливым равенство (6), докажем, что верна формула
Умножая обе части равенства (6) на 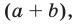
Следовательно,
Сравнивая правые части равенств (8) и (9), заключаем, что для доказательства формулы (8) достаточно показать, что
Используя (7), находим
Равенство (10) доказано и поэтому справедливо равенство (8). Итак, формула (6) верна при любом 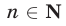
т.е.
Поэтому формулу (6) можно записать в виде
Из (11) следует, что 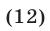
Возможно вам будут полезны эти страницы:
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института