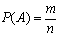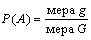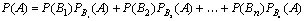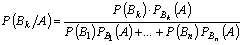Что такое полная система событий информатика
Полная группа событий
По́лной гру́ппой собы́тий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна 1.
Определение
Пусть 


Пример
Предположим, проводится подбрасывание монеты. В результате этого эксперимента обязательно произойдет одно из следующих событий:
Таким образом, система 
Полезное
Смотреть что такое «Полная группа событий» в других словарях:
Группа Дятлова — Гибель тургруппы Дятлова событие, случившееся в ночь с 1 на 2 февраля 1959 года на Северном Урале, когда при загадочных обстоятельствах погибла группа туристов, возглавляемая Игорем Дятловым. Причина гибели не ясна до сих пор. Перевал, рядом с… … Википедия
Сплин (группа) — Сплин Основная информация Жанр … Википедия
Машина времени (группа) — У этого термина существуют и другие значения, см. Машина времени (значения). Машина времени … Википедия
Инь-Ян (группа) — Эта статья о группе. О взаимодействии крайних противоположностей см. Инь Ян. Инь Ян Жанры поп музыка Годы 25 ноября 2007 по … Википедия
Последовательность событий 11 сентября 2001 года — Здесь приведена хронология теракта 11.09.01, в котором самолёт разрушил одну из башен близнецов торгового центра в Нью Йорке. Дано местное Нью Йоркское время. Содержание 1 События 1.1 6:00 AM 1.2 7:00 AM 1.3 8:00 AM 1.4 9:00 AM … Википедия
Хронология событий 11 сентября 2001 года — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Здесь приведен … Википедия
Случайное событие — Случайное событие подмножество множества исходов случайного эксперимента; при многократном повторении случайного эксперимента частота наступления события служит оценкой его вероятности. Случайное событие, которое никогда не реализуется в… … Википедия
Террористические акты 11 сентября 2001 года — Террористические акты 11 сентября 2001 года … Википедия
полная система событий
Смотреть что такое «полная система событий» в других словарях:
Полная группа событий — Полной группой событий в теории вероятностей называется система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна 1.… … Википедия
система — 4.48 система (system): Комбинация взаимодействующих элементов, организованных для достижения одной или нескольких поставленных целей. Примечание 1 Система может рассматриваться как продукт или предоставляемые им услуги. Примечание 2 На практике… … Словарь-справочник терминов нормативно-технической документации
Валютная система — (Monetary system) Валютная система это правовая форма организации валютных отношений Валютная система: Ямайская, Европейская, Бреттон Вудская, Парижская, Генуэзская, Российская Содержание >>>>>>>>>> … Энциклопедия инвестора
Ипотечная система — порядок приобретения прав на недвижимые имущества путем записки в публичных поземельных книгах. Термин И. система не вполне соответствует содержанию института, который регулирует приобретение всякого рода вещных прав на недвижимые имущества,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Избирательная система 1907 года — система выборов по Положению о выборах в Государственную Думу от 03 июня 1907 года, принятому после роспуска II Думы (см. Третьеиюньский переворот). Избирательная система использовалась при выборах в Государственные Думы III и IV созыва.… … Википедия
Медицина — I Медицина Медицина система научных знаний и практической деятельности, целями которой являются укрепление и сохранение здоровья, продление жизни людей, предупреждение и лечение болезней человека. Для выполнения этих задач М. изучает строение и… … Медицинская энциклопедия
ЭКВИВАЛЕНТНЫЕ ПРЕОБРАЗОВАНИЯ — управ ляющих систем преобразования, сохраняющие отношение эквивалентности (о. э.) управляющих систем (у. с.). Используются в задачах оптимизации, контроля, а также как средство характеризации (напр., аксиоматизации) определенных классов у. с.;… … Математическая энциклопедия
Относительности теория — физическая теория, рассматривающая пространственно временные свойства физических процессов. Закономерности, устанавливаемые О. т., являются общими для всех физических процессов, поэтому часто о них говорят просто как о свойствах… … Большая советская энциклопедия
Аренда — (Rent) Понятие аренды, аренда квартир, помещений, договор аренды Информация о понятии аренды квартир, помещений, составление договора аренды Содержание Содержание Аренда Объект Форма Стороны соглашения договоренности Виды ренты Экономическая… … Энциклопедия инвестора
Террористические акты 11 сентября 2001 года — Террористические акты 11 сентября 2001 года … Википедия
Буддийская космология — Буддизм … Википедия
Полная система событий
Р(А) + Р( 



Cумма вероятностей двух противоположных событий равна единице.
= 






Отсюда можно сделать вывод, который обосновывается строгим доказательством:
Сумма вероятностей событий, образующих полную группу событий равна единице.
Дата добавления: 2014-11-24 ; просмотров: 11 | Нарушение авторских прав
Полная группа событий
Сумма вероятностей всех событий в группе всегда равна 1.
Связанные понятия
В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.
В теории вероятностей говорят, что событие почти достоверно или что оно произойдет почти наверняка, если это произойдет с вероятностью 1. Понятие является аналогом понятия «почти всюду» в теории меры. В то время, как во многих основных вероятностных экспериментах нет никакой разницы между «почти достоверно» и «достоверно», (то есть, событие произойдет совершенно точно), это различие важно в более сложных случаях, относящихся к случаям рассмотрения какой-либо бесконечности. Например, термин часто.
Случайность имеет множество применений в области науки, искусства, статистики, криптографии, игр, азартных игр, и других областях. Например, случайное распределение в рандомизированных контролируемых исследованиях помогает ученым проверять гипотезы, а также случайные и псевдослучайные числа находят применение в видео-играх, таких как видеопокер.
В математике теория момента остановки или марковский момент времени связана с проблемой выбора времени, чтобы принять определённое действие, для того чтобы максимизировать ожидаемое вознаграждение или минимизировать ожидаемые затраты. Проблема момента остановки может быть найдена в области статистики, экономики и финансовой математики (связанные с ценообразованием на американские опционы). Самым ярким примером, относящимся к моменту остановки, является Задача о разборчивой невесте. Проблема момента.
Тема 8. СОБЫТИЕ И ВЕРОЯТНОСТЬ
8.1. Понятие о случайном событии
Наблюдение явления, опыт, эксперимент, которые можно провести многократно, в теории вероятностей принято называть испытанием. Примеры: сдача экзамена, наблюдение за дорожно-транспортными происшествиями, выстрел из винтовки, бросание игрального кубика, педагогический эксперимент.
Результат, исход испытания называется событием. Примеры: успешная сдача экзамена, дорожно-транспортные происшествия со смертельным исходом, попадание в цель, появление того или иного числа очков на брошенной игральной кости, получение результата при проведении педагогического эксперимента.
Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании. Примеры: совместные события: идет дождь и идет снег, человек ест и человек читает, число целое и четное; несовместные события: день и ночь, человек читает и человек спит, число иррациональное и четное.
Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Примеры: если сейчас день, то сейчас не ночь; если человек спит, то в данный момент он не читает; если число иррациональное, то оно не является четным.
Событие называется достоверным, если в данном испытании оно является единственно возможным его исходом. Событие называется невозможным, если в данном испытании оно заведомо не может произойти. Примеры: если в урне все шары белые, то достать белый шар является достоверным событием, а достать черный шар является невозможным событием; если человек прыгнул в воду, то выйти мокрым является достоверным событием, а выйти сухим является невозможным событием.
Событие называется случайным, если его наступление или ненаступление в некотором испытании (эксперименте) зависит от ряда случайных факторов. Примеры: успешная сдача экзамена; выигрыш в лотерее; рождения мальчика или девочки; всхожесть семян; попадание в цель и т. д.
8.2. Определение вероятности 
События, образующие полную группу попарно несовместных и равновозможных событий, будем называть элементарными событиями.
Классическое определение вероятности
Вероятностью P(A) события A называется отношение числа элементарных событий m, благоприятствующих событию A, к числу всех элементарных событий n:
Вероятность достоверного события равна 1.
Вероятность невозможного события равна 0.
Вероятность случайного события больше 0 и меньше 1.
Статистическое определение вероятности
Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Например, оно неприемлемо, если результаты испытания не равновозможны. В таких случаях используется статистическое определение вероятности. Пусть проводится n опытов, событие A наступило m раз, тогда
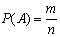
Геометрическое определение вероятности
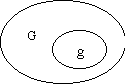
Если в результате проведения испытаний наблюдается произвольный исход из некоторого бесконечного множества, то можно сказать, что пространство элементарных исходов может быть некоторой областью G, а под событием А можно понимать исходы, входящие в область g. Пусть на область G наугад брошена «точка»; приняв равновозможность вариантов, естественно считать, что вероятность попадания в область g можно найти по формуле, называемой геометрической вероятностью:
Области могут быть различной размерности (одно-, двух- или трехмерного измерения) и, в зависимости от выбора размерности меры, могут принимать значения либо длины, либо площади, либо объема. Для конкретного испытания размерность мер g и G должна быть одна.
8.3. Свойства вероятности 
Теорема. Вероятность суммы двух несовместных событий A и B равна сумме вероятностей этих событий: P (A + B) = P(A) + P(B).
Следствие. Сумма вероятностей противоположных событий А и равна единице:
Вероятность суммы полной группы событий равна 1.
Произведением событий А и В называется событие С = АВ, состоящее в том, что в результате испытания произошло и событие А и событие В.
Два события A и B называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события A и B называются зависимыми.
Чаще всего зависимые испытания происходят тогда, когда тянут из одной колоды, не возвращая карты в колоду, вытаскивают из одной урны и т. д.
Теорема. Вероятность произведения двух независимых событий A и B равна произведению их вероятностей:
Теорема. Вероятность произведения двух зависимых событий A и B равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило:
Теорема. Вероятность суммы двух совместных событий A и B равна сумме вероятностей этих событий минус вероятность их произведения
Теорема (формула полной вероятности). Вероятность события A, которое может наступить лишь при условии появления одного из n попарно несовместных событий B1, B2,…, Bn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:
Вопросы 
1. Может ли событие быть одновременно и невозможным и достоверным?
2. Входит ли в понятие суммы событий (А + В) событие, состоящее в одновременном наступлении события А и события В?
3. Приведите пример полной группы событий для выбранного Вами испытания.
4. Исходя из формулы определения вероятности, объясните, почему значение вероятности находится в пределах от 0 до 1.
5. Часто ли случается, что наступление какого-либо события зависит от ряда причин? Приведите пример.
6. С помощью какой формулы можно выяснить наиболее вероятную причину уже наступившего события?