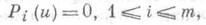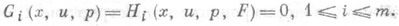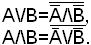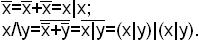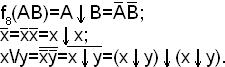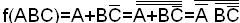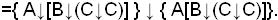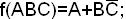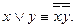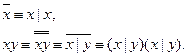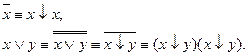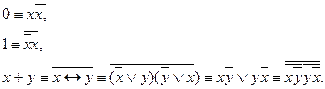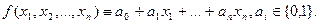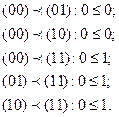Что такое полная система
Полная система функций
Смотреть что такое «Полная система функций» в других словарях:
ПОЛНАЯ СИСТЕМА ФУНКЦИЙ — ортонормированная система функций
ПОЛНАЯ СИСТЕМА ФУНКЦИИ — см. в ст. Ортогональная система функций. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия
система — 4.48 система (system): Комбинация взаимодействующих элементов, организованных для достижения одной или нескольких поставленных целей. Примечание 1 Система может рассматриваться как продукт или предоставляемые им услуги. Примечание 2 На практике… … Словарь-справочник терминов нормативно-технической документации
система кондиционирования воздуха — Совокупность воздухотехнического оборудования, предназначенная для кондиционирования воздуха в помещениях [ГОСТ 22270 76] система кондиционирования воздуха Совокупность технических средств для обработки и распределения воздуха, а также… … Справочник технического переводчика
Система компьютерной алгебры — Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Добавить иллюстрации. Викифицировать список литературы, используя … Википедия
Система автоматизации документооборота — Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Система ав … Википедия
ПОЛНАЯ СИСТЕМА

со следующим свойством: для любого набора чисел ( х, и, р), удовлетворяющего уравнениям (1), справедливы равенства
Если и=и (х) — совместное решение двух уравнений
то иявляется решением и уравнения

Произвольную систему вида (1) обычно пытаются расширить до полной добавлением к ней новых независимых уравнений, полученных из старых с помощью операции образования скобок Якоби. При этом расширении в соответствии с (2) ни одно из решений переходной системы не должно теряться, если она вообще разрешима.
есть диффеоморфизм 
Лит.:[1] Камке Э., Справочник по дифференциальным уравнениям в частных производных первого порядка, пер. с нем., М., 1966; [2] Гюнтер Н. М., Интегрирование уравнений первого порядка в частных производных, Л.- М., 1934; [3] Caratheodory С., Variationsrechnung und partielle Differentialgleichungen erster Ordnung, 2 Aufl., Bd 1, Lpz., 1956; [4] Gоursat E., Lemons sur 1’integration des equations aux derivdes partielles du premier ordre, P., 1891. А. П. Солдатов.
Полезное
Смотреть что такое «ПОЛНАЯ СИСТЕМА» в других словарях:
полная система — полный набор — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы полный набор EN complete set … Справочник технического переводчика
Полная система (музыка) — Полная система (греч. σύστημα τέλειον, лат. constitutio tota), или Полный звукоряд, в древнегреческой теории музыки (гармонике) звукоряд в полном объёме составляющих его ступеней (в оригинальных терминах «струн»), схематическое представление… … Википедия
ПОЛНАЯ СИСТЕМА ФУНКЦИИ — см. в ст. Ортогональная система функций. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия
полная система уравнений — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN complete system of equations … Справочник технического переводчика
Полная система коммутирующих наблюдаемых — (ПСКН) множество перестановочных (коммутирующих) самосопряжённых операторов, описывающих квантовые наблюдаемые и определяющих обобщённый базис пространства чистых состояний квантовой системы. Это понятие впервые было предложено Дираком и… … Википедия
ПОЛНАЯ СИСТЕМА ФУНКЦИЙ — ортонормированная система функций
Полная система функций — такая система функций Ф = <φ(x:)>, определённых на отрезке [a, b], что не существует функции f (x), для которой, х) из Ф, т. е. для которой при любой функции φ(х) из Ф (интегралы понимаются в смысле Лебега, см. Интеграл) … Большая советская энциклопедия
Полная система вычетов — по модулю m, любая совокупность целых чисел, содержащая по одному числу из каждого класса чисел по модулю m (два целых числа а и b принадлежат одному классу по модулю m, если а b делится на m; см. Вычет). В качестве П. с. в. чаще всего… … Большая советская энциклопедия
Полные системы функций. Теорема Поста о полной системе функций
Содержание
Полные системы функций [ править ]
| Определение: |
| Если любая булева функция, являющаяся суперпозицией функций некоторого множества, принадлежит этому множеству, то такое множество называют замкнутым (англ. closed set). |
| Определение: |
| Замыканием (англ. сlosure) множества функций называется минимальное по включению замкнутое подмножество всех функций, содержащее данное множество функций. |
| Определение: |
| Множество булевых функций называется полной системой (англ. complete set), если замыкание этого множества совпадает с множеством всех функций. |
| Определение: |
| Полная система функций называется безызбыточной (англ. irredundant functions), если она перестает быть полной при исключении из неё любого элемента. |
Американский математик Эмиль Пост сформулировал необходимое и достаточное условие полноты системы булевых функций. Для этого он ввел в рассмотрение следующие замкнутые классы булевых функций:
Замкнутые классы булевых функций [ править ]
Количество линейных функций от [math]n[/math] переменных равно [math]
Функция является линейной тогда, и только тогда, когда в ее полиноме Жегалкина присутствуют слагаемые, каждое из которых зависит не более чем от одной переменной. Построить полином Жегалкина можно с помощью преобразования Мебиуса.
Формулировка и доказательство критерия Поста [ править ]
Необходимость.
Заметим, что необходимость этого утверждения очевидна, так как если бы все функции из набора [math]K[/math] входили в один из перечисленных классов, то и все суперпозиции, а, значит, и замыкание набора входило бы в этот класс, и набор [math]K[/math] не мог бы быть полным.
Достаточность.
Докажем, что если набор [math]K[/math] не содержится полностью ни в одном из данных классов, то он является полным.
Таким образом, возможны четыре варианта:
Рассмотрим несколько вариантов:
Значит, полученные функции образуют полную систему, поскольку с их помощью можно выразить любую булеву функцию. Из этого следует, что K — полная система функций, что и требовалось доказать.
Примеры [ править ]
В частности, если функция не входит ни в один из классов Поста, она сама по себе формирует полную систему. В качестве примера можно назвать штрих Шеффера или стрелку Пирса.
Широко известны такие полные системы булевых функций:
Первая система используется, например, для представления функций в виде дизъюнктивных и конъюнктивных нормальных форм, вторая — для представления в виде полиномов Жегалкина.
Первая из упоминавшихся выше полных систем безызбыточной не является, поскольку согласно законам де Моргана либо дизъюнкцию, либо конъюнкцию можно исключить из системы и восстановить с помощью остальных двух функций. Вторая система является безызбыточной — все три её элемента необходимы для полноты системы.
Теорема о максимальном числе функций в базисе: максимально возможное число булевых функций в базисе — четыре.
Иногда говорят о системе функций, полной в некотором замкнутом классе, и, соответственно, о базисе этого класса. Например, систему [math]\left\<\oplus,1\right\>[/math] можно назвать базисом класса линейных функций.
Полные системы булевых функций



Для того чтобы система булевых функций была полной, необходимо и достаточно, чтобы она содержала:
— хотя бы одну функцию, не сохраняющую константу нуль;
— хотя бы одну функцию, не сохраняющую константу единица;
— хотя бы одну функцию, не являющуюся линейной;
— хотя бы одну функцию, не являющуюся монотонной;
— хотя бы одну функцию, не являющуюся самодвойственной.
Это критерий полноты системы.
Будем рассматривать функции, зависящие от n аргументов. Число различных функций равно 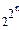
Тривиальная полная система состоит из всех 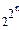
Функции инверсии, дизъюнкции и конъюнкции образуют полную систему. Это вытекает из основной теоремы, утверждающей, что любая булева функция может быть записана в виде дизъюнкции минтермов (или конъюнкции макстермов).
Базис < /\,\/,¯ >не минимален, так как может быть уменьшен за счет выбрасывания из него /\ или \/. Это следует из формул де Моргана:
Базисы и <\/,¯>являются минимальными.
б) функция импликации и константа 1:
в) функция импликации и инверсии :
f14(xy)=x | y= 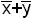
Доказательство. Выразим ¯ и /\ через функцию Шеффера:
Так как <¯,/\>– полная система, утверждение доказано.
Пример. Выразим функцию, используя только функцию Шеффера:
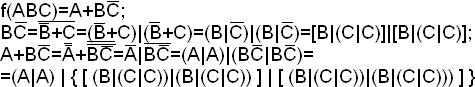
Так как инверсия и дизъюнкция выражаются только через функцию «стрелка Пирса», а <¯,\/>– функционально полная система, то А↓В является функционально полной системой.
Пример. Выразить функцию, используя только функцию «стрелка Пирса»:
Выбор функционально полной системы по таблице.
Обе функции самодвойственны. Система <
Если fk(11…1) = 1, то эта же функция не самодвойственна, так как fk(00…0)≠0.
Если же fk(11…1) = 0, то эта же функция не сохраняет константу 1 и не монотонна.
Присоединив к fk недостающие три функции, получим систему, состоящую не более чем из четырех функций.
Пример. Составить минимальный базис, включающий функцию
Базисы
Пример. Выразить функцию в системе
Для преобразований используем систему <\/,/\,¯>как основную:



ТЕМА: ПОЛНОТА МНОЖЕСТВА ФУНКЦИЙ.
2. Критерий полноты системы булевых функций.
3. Независимые системы. Базис замкнутого класса.
1. Полная система. Достаточное условие полноты.
Познакомясь с понятиями ДНФ, КНФ, СДНФ, СКНФ, полином Жегалкина выяснили, что любую булеву функцию можно выразить в виде формулы через элементарные функции : отрицание, конъюнкцию, дизъюнкцию, двоичное сложение и константу 0 или 1.
Эти функции можно рассматривать как систему элементарных функций, через которые выражается любая булева функция.
Возникает вопрос: в какой мере является случайным наличие таких систем элементарных функций?
Дадим определение таких систем.
Система булевых функций
Составление сложных функций из элементарных функций системы называется суперпозицией.
Познакомимся с достаточным условием полноты системы.
Полнота первой системы следует из того, что любую булеву функцию можно представить в виде ДНФ или КНФ.
С помощью той же полной системы докажем полноту <-, L>. Для этого нужно выразить дизъюнкцию:
Для доказательства полноты системы <-, ®>воспользуемся полной системой <-, V>. Выразим дизъюнкцию: 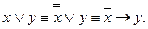
Для доказательства полноты системы
При доказательстве полноты системы
2. Критерий полноты системы булевых функций.
Мы рассмотрели лишь достаточное условие полноты системы. Перейдем теперь к установлению критерия полноты. Прежде познакомимся с понятиями замыкания и замкнутого класса.
Пусть К – некоторое подмножество элементарных функций. Замыканием подмножества К называется множество булевых функций, представимых в виде формул через функции К. Обозначение замыкания : [K].
Можно теперь сформулировать еще одно определение полной системы:
Множество К называется функционально замкнутым (или просто замкнутым), если его замыкание – само множество К..
Дадим еще одно определение замкнутого множества (класса).
Класс К булевых функций называется замкнутым, если вместе с функциями из этого класса он содержит и все их суперпозиции, т.е. элементарные суперпозиции не выводят из этого класса. К элементарным суперпозициям относятся:
1. переименование некоторой переменной какой-нибудь функции рассматриваемой системы;
2. подстановка некоторой функции из этой системы вместо некоторой переменной любой из функции этой системы.
К замкнутым классам относятся: множество всех булевых функций Р2; класс функций от одной переменной; класс, содержащий только тождественные функции вида f(X)=X.
Приведем следующее утверждение:
Никакая полная система функций не может содержаться в функционально замкнутом классе, отличном от класса Р2 всех булевых функций.
Рассмотрим некоторые функционально замкнутые классы функций, которые называются важнейшими замкнутыми классами. Они используются в критерии полноты.
Класс Т0 – класс функций, сохраняющих 0, т.е. f(0,0,…0)=0.
Примеры функций, принадлежащих к Т0: 0, х, ху=00=0, xvy=0v0=0, x+y=0+0=0.
Функции, не принадлежащие к Т0: 1, x|y=0|0=1, x¯y=0¯0=1.
Класс Т1— класс функций, сохраняющих 1, т.е. f(1,1,…,1)=1.
Примеры функций, не принадлежащих классу Т1: 0, x|y=1|1=0, x¯y=1¯1=0.
Класс S – класс самодвойственных функций.
Самодвойственной функцией называется функция f(x1, x2, …,xn), если f(x1, x2, …,xn) º f*(x1, x2, …,xn), где 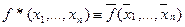
Функции ху, xvy, x®y не относятся к самодвойственным функциям.
Класс L – класс линейных функций.
Функция называется линейной, если равносильная ей функция, являющаяся полиномом содержит конъюнкции не выше первой степени, т. е.
К линейным относятся: 1, 0, х, 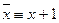
Функции 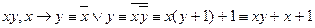
Класс монотонных функций M.
Введем отношение частичного порядка на множестве упорядоченных наборов (векторов).
Например, 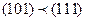
Говорят так же, что a и b сравнимы.
Функция f(x1, x2, …,xn) называется монотонной, если любых векторов a и b списка переменных таких, что 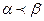
К монотонным относятся, например, функции : х, ху, xvy.
Проверим монотонность xy и xvy. Составим таблицы истинности :
По таблице истинности легко установить монотонность и этой функции.
Функция х®у не является монотонной, т.к. 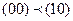
Любые элементарные суперпозиции не выводят из рассмотренных классов. Тем самым доказывается их функциональная замкнутость.
Чтобы доказать полноту какой-либо системы, оказывается, можно ограничится рассмотренными пятью классами. Итак, рассмотрим критерий полноты (теорему Поста), который является необходимым и достаточным условием полноты системы булевых функций.
Для того, чтобы система булевых функций была полной, необходимо и достаточно, чтобы для каждого из классов Т0, Т1, S, L, M нашлась функция fi из этой системы не принадлежащая этому классу.
Для доказательства полноты с помощью теоремы Поста, нужно составить таблицу, которая называется таблицей Поста: по горизонтали перечислены замкнутые классы, по вертикали – функции системы. В ячейке ставят минус, если функция не принадлежит классу, и плюс, если принадлежит.
Рассмотрим пример: докажем полноту системы <+, v, 1,0>.
| f | T0 | T1 | S | L | M |
| x+y | + | — | — | + | — |
| xvy | + | + | — | — | + |
| — | + | — | + | + | |
| + | — | — | + | + |
Для 0 и 1 таблица заполняется тривиально. Не составляет труда проверить принадлежность х+у и xvy к Т0 и Т1. Более подробно покажем заполнение оставшихся ячеек.
S: 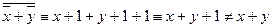
M: составим таблицу истинности:
Функция не монотонная, т.к., например, 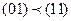
S: для xvy двойственной является ху, следовательно, х+уÏS;
L: 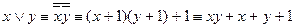
Принадлежность этой функции мы уже доказали в выше рассмотренном примере.
Итак, т.к. в каждом столбце есть хотя бы один минус, означает полноту данной системы.
3. Независимые системы. Базис замкнутого класса.
Система функций G называется независимой, если никакая функция fÎG не представима суперпозициями функций из G\f.
Примеры независимых систем:
Независимая система функций G называется базисом замкнутого класса К, если всякая функция из К есть суперпозиция функций из G.
Например, системы <-, V>, <-, L>являются базисом для класса Р2, т.к. системы полные и независимые.
Система <+, v, 1,0>не является базисом для Р2, т.к. хотя она полная, но не является независимой: можно удалить 0. значит базисом для Р2 является система <+, v, 1>.
Функции, образующие базис во множестве всех булевых функций Р2, называются шефферовыми функциями.
Например, функции x|y и х¯у – шефферовые, т.к. каждая из них образует полную систему (было доказано выше), причем, независимую.
Функция х®у не является шефферовой, т. к. не образует полную систему: 1®1=1, т.е. х®уÎТ1.
Задачи для самостоятельного решения.
1. Выразить импликацию через функции системы <1, +, L>.
2. Выразить дизъюнкцию и конъюнкцию через функции системы <-, ®>.
3. С помощью достаточного условия полноты проверить на полноту систему а) <0, v, ®>; б) <-, «>; в) <0, +, L>.
5. Является ли система <1,0,+,L>базисом множества всех булевых функций?
6. Являются ли функции х«у, ху, xvy, 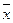
1. Что называется замыканием множества булевых функций?
2. Перечислить свойства замыкания.
3. Что такое суперпозиция? Какие суперпозиции относятся к элементарным?
4. Сформулировать два определения функционально замкнутого класса.
6. Перечислить все важнейшие замкнутые классы. Привести примеры функций принадлежащих и не принадлежащих к каждому замкнутому классу.
7. Сформулировать теорему Поста. Что собой представляет таблица Поста?
8. Какая система булевых функций называется независимой?