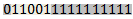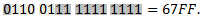Что такое половинная точность
Число половинной точности
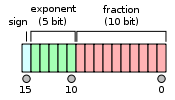
Число́ полови́нной то́чности (англ. half precision ) — компьютерный формат представления чисел, занимающий в памяти половину компьютерного слова (в случае 32-битного компьютера — 16 бит или 2 байта). Диапазон значений ± 2 −24 (5.96E-8) — 65504. Приблизительная точность — 3 знака (10 двоичных знаков, log10(2 11 )).
| Знак | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Экспо- нента | Мантисса | ||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 | 8 | 7 | 0 | ||||||||||||
Примеры чисел половинной точности
Данные примеры представлены в битовом виде числа с плавающей запятой. Они включают в себя бит знака, экспоненту и мантиссу.
По умолчанию, 1/3 округляется вниз.
Пределы точности на целых числах
Целые между 0 и 2047 представляются точно
Целые между 2048 и 4095 округляются вниз до ближайшего кратному 2 (четному числу)
Целые между 4096 и 8191 округляются вниз до ближайшего кратному 4
Целые между 8192 и 16383 округляются вниз до ближайшего кратному 8
Целые между 16384 и 32767 округляются вниз до ближайшего кратному 16
Целые между 32768 и 65535 округляются вниз до ближайшего кратному 32
См. также
Полезное
Смотреть что такое «Число половинной точности» в других словарях:
Число двойной точности — (Double precision, Double) компьютерный формат представления чисел, занимающий в памяти две последовательных ячейки (компьютерных слова; в случае 32 битного компьютера 64 бита или 8 байт). Как правило, обозначает формат числа с плавающей запятой… … Википедия
Число одинарной точности — (англ. Single precision, Single) широко распространенный компьютерный формат представления вещественных чисел, занимающий в памяти 32 бита (4 байта). Как правило, под ним понимают формат числа с плавающей запятой стандарта IEEE 754.… … Википедия
Число четверной точности — (англ. Quadruple precision) компьютерный формат представления чисел с плавающей запятой, занимающий в памяти четыре последовательных ячейки (компьютерных слова; в случае 32 битного компьютера 128 бит или 16 байт). Как правило, обозначает… … Википедия
Число с плавающей запятой — Число с плавающей запятой форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную.… … Википедия
Числа с плавающей запятой — Плавающая запятая форма представления действительных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее… … Википедия
Запятая плавающая — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Машинный эпсилон — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Плавающая запятая — форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто используемое представление… … Википедия
Плавающая точка — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Числа с плавающей точкой — Плавающая запятая форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто… … Википедия
Они могут выражать значения в диапазоне ± 65 504, при этом минимальное значение выше 1 составляет 1 + 1/1024.
В зависимости от компьютера, половинная точность может быть более чем на порядок быстрее, чем двойная точность, например, 550 PFLOPS для половинной точности против 37 PFLOPS для двойной точности на одном облачном провайдере.
СОДЕРЖАНИЕ
IEEE 754 двоичный формат с плавающей запятой половинной точности: binary16
Стандарт IEEE 754 определяет двоичный файл16 как имеющий следующий формат:
Формат выложен следующим образом:
Экспонентное кодирование
Двоичная экспонента с плавающей запятой половинной точности кодируется с использованием двоичного представления смещения с нулевым смещением, равным 15; также известный как смещение экспоненты в стандарте IEEE 754.
Таким образом, как определено двоичным представлением смещения, чтобы получить истинную экспоненту, смещение 15 должно быть вычтено из сохраненной экспоненты.
Сохраненные экспоненты 00000 2 и 11111 2 интерпретируются особым образом.
Примеры половинной точности
Эти примеры даны в битовом представлении значения с плавающей запятой. Это включает знаковый бит, (смещенную) экспоненту и мантиссу.
Ограничения точности десятичных значений в [0, 1]
Ограничения точности десятичных значений в [1, 2048]
Ограничения точности для целочисленных значений
Альтернативный вариант ARM с половинной точностью
Процессоры ARM поддерживают (через бит регистра управления с плавающей запятой ) «альтернативный формат половинной точности», который устраняет особый случай для значения экспоненты 31 (11111 2 ). Он почти идентичен формату IEEE, но в нем нет кодирования для бесконечности или NaN; вместо этого показатель степени 31 кодирует нормализованные числа в диапазоне от 65536 до 131008.
Использует
Аппаратное и программное обеспечение для машинного обучения или нейронных сетей, как правило, использует половинную точность: такие приложения обычно выполняют большой объем вычислений, но не требуют высокого уровня точности.
На старых компьютерах, которые обращаются к 8 или 16 битам за раз (большинство современных компьютеров обращаются к 32 или 64 битам за раз), арифметика половинной точности выполняется быстрее, чем одинарная точность, и значительно быстрее, чем двойная точность. В системах с инструкциями, которые могут обрабатывать несколько чисел с плавающей запятой в одной инструкции, половинная точность часто обеспечивает более высокую среднюю пропускную способность.
Число в формате половинной точности
Правила ввода чисел
Число́ полови́нной то́чности (англ. half precision ) — компьютерный формат представления чисел, занимающий в памяти половину компьютерного слова (в случае 32-битного компьютера — 16 бит или 2 байта). Диапазон значений ± 2 −24 (5.96E-8) — 65504. Приблизительная точность — 3 знака (10 двоичных знаков, log10(2 11 )).
| Знак | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Экспо- нента | Мантисса | |||||||||||||
| 15 | 8 | 7 | ||||||||||||
Содержание
Кодирование поля Exponent [ править | править код ]
Числа half-precision binary floating-point кодируют поле Exponent с использованием сдвига (bias) на 15.
Другими словами, для получения настоящего порядка (для Exponent от 000012 до 111102) надо из закодированного поля Exponent вычесть 15 (т.е. 011112).
С помощью значений 000002 и 111112 поля Exponent кодируют специальные случаи.
Максимальное представляемое значение = (2−2 −10 ) × 2 15 = 65504.
Примеры чисел половинной точности [ править | править код ]
В данных примерах числа с плавающей запятой представлены в двоичном представлении. Они включают в себя бит знака, экспоненту и мантиссу.
По умолчанию, 1/3 округляется вниз.
Пределы точности на целых числах [ править | править код ]
Целые между 0 и 2047 представляются точно
Целые между 2048 и 4095 округляются вниз до ближайшего кратному 2 (четному числу)
Целые между 4096 и 8191 округляются вниз до ближайшего кратному 4
Целые между 8192 и 16383 округляются вниз до ближайшего кратному 8
Целые между 16384 и 32767 округляются вниз до ближайшего кратному 16
Целые между 32768 и 65535 округляются вниз до ближайшего кратному 32
Смещение (или сдвиг) порядка: 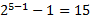
Формат числа одинарной точности
Под порядок выделено 8 бит, поэтому смещение: 
Формат двойной точности
Под порядок выделено 11 бит, поэтому смещение: 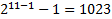
Алгоритм получения числа с плавающей точкой
1. Перевести число из K-ичной системы счисления в двоичную (прямой код);
2. Представить двоичной число в нормализованной форме: 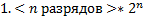
3. Рассчитать смещенный порядок числа: 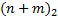
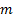
4. Разместить знак, порядок и мантиссу в соответствующие разряды сетки;
5. Разбить полученное число на тетрады и записать полученные двоичные разряды в виде числа в 16-ичной системе.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9636 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Представление вещественных чисел
Вещественные числа обычно представляются в виде чисел с плавающей запятой. Числа с плавающей запятой — один из возможных способов представления действительных чисел, который является компромиссом между точностью и диапазоном принимаемых значений, его можно считать аналогом экспоненциальной записи чисел, но только в памяти компьютера.
Число с плавающей запятой состоит из набора отдельных двоичных разрядов, условно разделенных на так называемые знак (англ. sign), порядок (англ. exponent) и мантиссу (англ. mantis). В наиболее распространённом формате (стандарт IEEE 754) число с плавающей запятой представляется в виде набора битов, часть из которых кодирует собой мантиссу числа, другая часть — показатель степени, и ещё один бит используется для указания знака числа ( [math]0[/math] — если число положительное, [math]1[/math] — если число отрицательное). При этом порядок записывается как целое число в коде со сдвигом, а мантисса — в нормализованном виде, своей дробной частью в двоичной системе счисления. Вот пример такого числа из [math]16[/math] двоичных разрядов:
| Знак | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 10 | 9 | 0 | ||||||||||||
Знак — один бит, указывающий знак всего числа с плавающей точкой. Порядок и мантисса — целые числа, которые вместе со знаком дают представление числа с плавающей запятой в следующем виде:
Порядок также иногда называют экспонентой или просто показателем степени.
При этом лишь некоторые из вещественных чисел могут быть представлены в памяти компьютера точным значением, в то время как остальные числа представляются приближёнными значениями.
Более простым вариантом представления вещественных чисел является вариант с фиксированной точкой, когда целая и вещественная части хранятся отдельно. Например, на целую часть отводится всегда [math]X[/math] бит и на дробную отводится всегда [math]Y[/math] бит. Такой способ в архитектурах процессоров не присутствует. Отдаётся предпочтение числам с плавающей запятой, как компромиссу между диапазоном допустимых значений и точностью.
Содержание
Нормальная и нормализованная форма [ править ]
Типы чисел с плавающей точкой (по IEEE 754) [ править ]
Число половинной точности (Binary16, Half precision) [ править ]
Число́ полови́нной то́чности — компьютерный формат представления чисел, занимающий в памяти половину машинного слова (в случае 32-битного компьютера — [math]16[/math] бит или [math]2[/math] байта). В силу невысокой точности этот формат представления чисел с плавающей запятой обычно используется в видеокартах, где небольшой размер и высокая скорость работы важнее точности вычислений.
| Знак | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | |||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 14 | 10 | 9 | 0 | |||||||||||||
Число одинарной точности (Binary32, Single precision, float) [ править ]
Число́ одина́рной то́чности — компьютерный формат представления чисел, занимающий в памяти одно машинное слово (в случае 32-битного компьютера — [math]32[/math] бита или [math]4[/math] байта). Используется для работы с вещественными числами везде, где не нужна очень высокая точность.
| Знак | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок (8 бит) | Мантисса (23+1 бита) | |||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 30 | 23 | 22 | 0 | |||||||||||||||||||||||||||||
Число двойной точности (Binary64, Double precision, double) [ править ]
Число́ двойно́й то́чности — компьютерный формат представления чисел, занимающий в памяти два машинных слова (в случае 32-битного компьютера — [math]64[/math] бита или [math]8[/math] байт). Часто используется благодаря своей неплохой точности, даже несмотря на двойной расход памяти и сетевого трафика относительно чисел одинарной точности.
| Знак | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок (11 бит) | Мантисса (52+1 бит) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 62 | 52 | 51 | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Число четверной точности (Binary128, Quadruple precision) [ править ]
Число́ четверно́й то́чности — компьютерный формат представления чисел, занимающий в памяти четыре машинных слова (в случае 32-битного компьютера — [math]128[/math] бит или [math]16[/math] байт). Используется в случае необходимости крайне высокой точности.
| Знак | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок (15 бит) | Мантисса (112+1 бит) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 126 | 112 | 111 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Мантисса (112+1 бит) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Обычно этот формат реализуется программно, случаи аппаратной реализации крайне редки. Также не гарантируется поддержка этого типа в языках программирования, хотя кое-где она и реализована (например, компилятор gcc для архитектуры x86 позволяет использовать тип __float128, являющийся программной реализацией числа с четверной точностью). В совокупности эти факторы делают Quadruple весьма экзотичным и редко встречающимся форматом чисел с плавающей запятой.
Диапазон значений чисел с плавающей запятой [ править ]
Данная таблица только лишь примерно указывает границы допустимых значений, без учета возрастающей погрешности с ростом абсолютного значения и существования денормализованных чисел.
Особые значения чисел с плавающей точкой [ править ]
Ноль (со знаком) [ править ]
Как уже было оговорено выше, в нормализованной форме числа с плавающей точкой невозможно представить ноль. Поэтому для его представления зарезервированы специальные значения мантиссы и порядка — число считается нулём, если все его биты, кроме знакового, равны нулю. При этом в зависимости от значения бита знака ноль может быть как положительным, так и отрицательным.
| Знак | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||||
| 0 /1 | 0 | 0 | 0 | 0 | 0 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = [math]\pm0[/math] |
| 14 | 10 | 9 | 0 | ||||||||||||||
Арифметика нуля со знаком
Арифметика отрицательного нуля аналогична таковой для любого отрицательного числа и понятна интуитивно. Вот несколько примеров:
Неопределенность (NaN) [ править ]
NaN — это аббревиатура от фразы «not a number«. NaN является результатом арифметических операций, если во время их выполнения произошла ошибка (примеры см. ниже). В IEEE 754 NaN представлен как число, в котором все двоичные разряды порядка — единицы, а мантисса не нулевая.
| Знак | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||||
| 0 /1 | 1 | 1 | 1 | 1 | 1 | 1, | 0 /1 | 0 /1 | 0 /1 | 0 /1 | 0 /1 | 0 /1 | 0 /1 | 0 /1 | 0 /1 | 0 /1 | = [math]NaN[/math] |
| 14 | 10 | 9 | 0 | ||||||||||||||
Любая операция с NaN возвращает NaN. При желании в мантиссу можно записывать информацию, которую программа сможет интерпретировать. Стандартом это не оговорено и мантисса чаще всего игнорируется.
Как можно получить NaN?
Есть и другие способы получения NaN, подробности можно найти по ссылкам в соответствующем разделе.
По определению NaN ≠ NaN, поэтому, для проверки значения переменной нужно просто сравнить ее с собой.
Бесконечности [ править ]
| Знак | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Порядок | Мантисса | ||||||||||||||||
| 0 /1 | 1 | 1 | 1 | 1 | 1 | 1, | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = [math]\pm\infty[/math] |
| 14 | 10 | 9 | 0 | ||||||||||||||
Денормализованные числа [ править ]
То есть число с плавающей запятой, при учете вышесказанного, можно задать следующим образом:
В современных процессорах обработка денормализованных чисел происходит в десятки раз медленнее, чем обработка нормализованных чисел. Ниже приведена часть таблицы из статьи Isaac Dooley, Laxmikant Kale «Quantifying the Interference Caused by Subnormal Floating-Point Values» [1]
| Производитель | Процессор | Замедление (разы) |
|---|---|---|
| IBM | PowerPC 970 | 2,4 |
| AMD | Athlon | 6,0 |
| Intel | Pentium 3 | 15,8 |
| AMD | Athlon 64 | 21,4 |
| AMD | Opteron64 | 23,8 |
| Intel | Core Duo | 44,2 |
| Intel | P4 Xeon | 97,9 |
| Intel | Pentium 4 | 131,0 |
| Intel | Itanium 2 | 183,2 |
| Sun | UltraSPARC IV | 520,0 |
В таблице приведены наихудшие результаты тестирования среди всех использованных компиляторов (gcc, icc, xlc) со всеми доступными флагами оптимизации. Исследователи утверждают, что различие среднего случая с худшим незначительно.
Поскольку в стандартных форматах (одинарной и двойной точности) денормализованные числа получаются действительно очень маленькими и практически никак не влияют на результат некоторых вычислений (при этом заметно замедляя их скорость), то иногда они просто игнорируются. При этом используются два простых механизма, получивших называние Flush-to-zero (FTZ) и Denormals-are-zero (DAZ). Первый механизм заставляет операции возвращать ноль, как только становится ясно, что результат будет денормализованным. Второй механизм заставляет операции рассматривать поступающие на вход денормализованные числа как нули.
Ярким примером подобного «отсечения» денормализованных чисел могут послужить видеокарты, в которых резкое падение скорости вычислений в сотню раз недопустимо. Так же, например, в областях, связанных с обработкой звука, нет нужды в очень маленьких числах, поскольку они представляют столь тихий звук, что его не способно воспринять человеческое ухо.
В версии стандарта IEEE 754-2008 денормализованные числа (denormal или denormalized numbers) были переименованы в subnormal numbers, то есть в числа, меньшие «нормальных». Поэтому их иногда еще называют «субнормальными«.
Действия с числами с плавающей запятой [ править ]
Умножение и деление [ править ]
Самыми простыми для восприятия арифметическими операциями над числами с плавающей запятой являются умножение и деление. Для того, чтобы умножить два вещественных числа в нормализованной форме необходимо перемножить их мантиссы, сложить порядки, округлить и нормализовать полученное число.
Соответственно, чтобы произвести деление нужно разделить мантиссу делимого на мантиссу делителя и вычесть из порядка делимого порядок делителя. Затем точно так же округлить мантиссу результата и привести его к нормализованной форме.
Сложение и вычитание [ править ]
Идея метода сложения и вычитания чисел с плавающей точкой заключается в приведении их к одному порядку. Сначала выбирается оптимальный порядок, затем мантиссы обоих чисел представляются в соответствии с новым порядком, затем над ними производится сложение/вычитание, мантисса результата округляется и, если нужно, результат приводится к нормализированной форме. Пример:
Алгоритм получения представления вещественного числа в памяти ЭВМ [ править ]
Покажем преобразование действительного числа для представления его в памяти ЭВМ на примере величины типа Double.
Как видно из таблицы, величина этого типа занимает в памяти [math]8[/math] байт. На рисунке ниже показано, как здесь представлены поля мантиссы и порядка (нумерация битов осуществляется справа налево):
| Знак | Смещённый порядок | Мантисса |
|---|---|---|
| 63 | 62..52 | 51..0 |
Таким образом, из вышесказанного вытекает следующий алгоритм для получения представления действительного числа в памяти ЭВМ:
Очевидно, что более компактно полученный код стоит записать следующим образом: C073850000000000(16).
Другой пример иллюстрирует обратный переход от кода действительного числа к самому числу.
Пример. Пусть дан код 3FEC600000000000(16) или
| 0 | 01111111110 | 1100011000000000000000000000000000000000000000000000 |
| 63 | 62..52 | 51..0 |