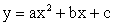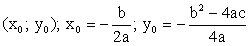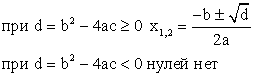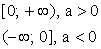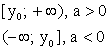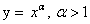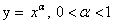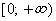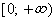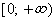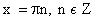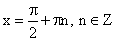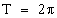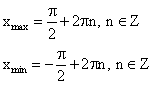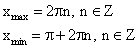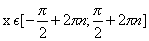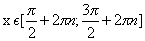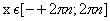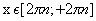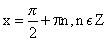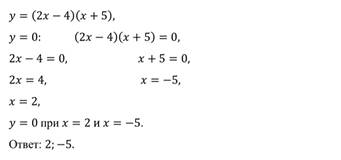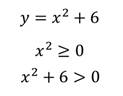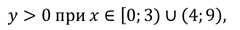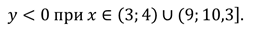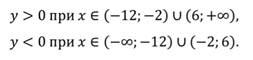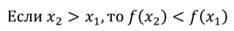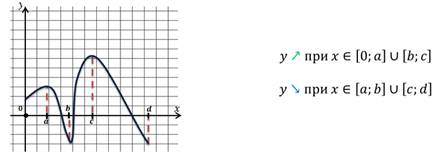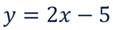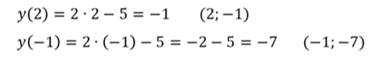Что такое положительная функция
Свойства функции. Возрастание и убывание, наибольшее и наименьшее значения, нули, промежутки знакопостоянства.
теория по математике 📈 функции
Каждый из нас встречался с разными графиками, как на уроках, так и в жизни. Например, рассматривали, как изменяется температура воздуха в определенный период времени.
На рисунке видно, что температура воздуха была отрицательной с 0 часов до 6 часов, а также с 20 до 24 часов. Еще можем сказать, что температура повышалась до 14 часов, а затем понижалась. То есть по данному графику мы смогли определить некоторые свойства зависимости температуры воздуха от времени суток.
Остановимся подробнее на свойствах функций.
Нули функции
Нули функции – это значение аргумента, при которых функция обращается в нуль. Если смотреть нули функции на графике, то берем точки, где график пересекает ось х.

Существует функция, которая не будет иметь нули функции. Это гипербола. Вспомним, что функция имеет вид у=k/x, где х не равное 0 число.
а) Для нахождения нулей функции необходимо в данную формулу вместо у подставить число 0, так как координаты точки пересечения графика с осью х (х;0). Нам нужно найти значение х. Получаем 0 = –11х +12. Решаем уравнение. Переносим слагаемое, содержащее переменную, в левую часть, меняя знак на противоположный: 11х=22
Находим х, разделив 22 на 11: х=22:11
Таким образом, мы нашли нуль функции: х=2
Пример №2. Найти нули функции у=f(x) по заданному графику.
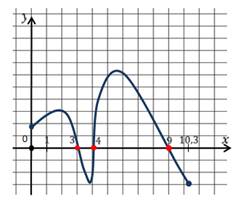
Находим точки пересечения графика с осью х и выписываем значения х в этих точках. Это (-4,9); (-1,2); 2,2 и 5,7. У нас на рисунке точки пересечения выделены красным цветом.
Промежутки знакопостоянства
Промежутки, где функция сохраняет знак (то есть значение y либо положительное на этом промежутке, либо отрицательное), называется промежутками знакопостоянства.
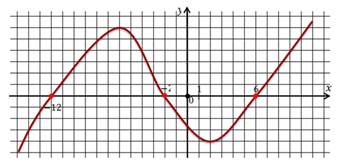
Пример №3. Найдем промежутки знакопостоянства по заданному на промежутке [-2; 10] графику функции у=f(x).
Функция принимает отрицательные значения в промежутках (-1; 3) и (8; 10]. Обратите внимание на линии синего цвета.
Возрастание и убывание функции
Значения функции могут уменьшаться или увеличиваться. Это зависит от того, как изменяются значения х. Рассмотрим это свойство по рисунку.
Посмотрим на значения х, которые увеличиваются от 2 до 5. В этом случае значения у уменьшаются. На графике эта часть выделена зеленым цветом. Слева направо эта часть графика идет вниз. То есть в промежутке [2;5] функция у=f(x) является убывающей.
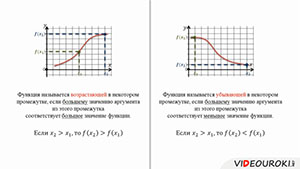
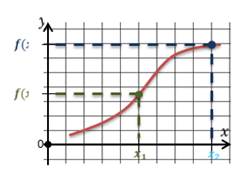
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
СОДЕРЖАНИЕ
Наиболее частое использование
, \ quad a_
В частности, необходимо (но не достаточно), чтобы
, \ квад | е (х) | \ leq f (0)>
(эти неравенства следуют из условия при n = 1, 2.)
Функция отрицательно определена, если неравенство обратное. Функция является полуопределенной, если сильное неравенство заменить слабым (≤, ≥ 0).
Примеры
Теорема Бохнера
Положительная определенность естественным образом возникает в теории преобразования Фурье ; непосредственно видно, что для положительной определенности достаточно, чтобы f было преобразованием Фурье функции g на вещественной прямой с g ( y ) ≥ 0.
Приложения
Обобщение
Можно определить положительно определенные функции на любой локально компактной абелевой топологической группе ; Теорема Бохнера распространяется и на этот контекст. Положительно определенные функции на группах естественным образом встречаются в теории представлений групп в гильбертовых пространствах (т. Е. Теории унитарных представлений ).
Альтернативное определение
Следующее определение противоречит приведенному выше.
Что такое положительная функция
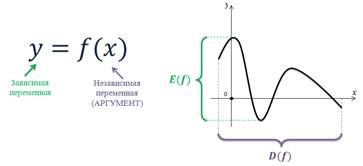
Функция
Область определения
Вершина параболы
Нули функции
Экстремумы
если a 0, то максимум в вершине
Область значений
Четность
ни четная, ни нечетная
Функция
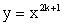
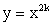
Область определения
Область значений
Четность
Нули функции
Экстремумы
х = 0 — точка минимума
Монотонность
возрастает при х ϵ R
при х ≤ 0 убывает
при х > 0 возрастает
Функция
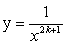
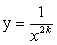
Область определения
Область значений
Четность
Нули функции
Экстремумы
Монотонность
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
возрастает при х ϵ D(f)
возрастает при х ϵ D(f)
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Четность
Периодичность
Экстремумы
Монотонность
Функция
Область определения
R кроме
R кроме
В математика, а положительно определенная функция является, в зависимости от контекста, одним из двух типов функция.
Содержание
Наиболее частое использование
, quad a_
В частности, необходимо (но недостаточно), чтобы
, квад | е (х) | leq f (0)>
(эти неравенства следуют из условия п = 1, 2.)
Функция отрицательно определенный если неравенство обратное. Функция полуопределенный если сильное неравенство заменить на слабое (≤, ≥ 0).
Примеры
Теорема Бохнера
Положительная определенность естественно возникает в теории преобразование Фурье; непосредственно видно, что для того, чтобы быть положительно определенным, достаточно, чтобы ж быть преобразованием Фурье функции г на реальной линии с г(у) ≥ 0.
Приложения
В этом контексте терминология Фурье обычно не используется, а вместо этого утверждается, что ж(Икс) это характеристическая функция из симметричный функция плотности вероятности (PDF).
Обобщение
Можно определить положительно определенные функции на любом локально компактная абелева топологическая группа; Теорема Бохнера распространяется и на этот контекст. Положительно определенные функции на группах естественным образом возникают в теория представлений групп на Гильбертовы пространства (т.е. теория унитарные представления).
В динамических системах
Свойства функций
Урок 2. Алгебра 9 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Свойства функций»
На прошлом уроке мы с вами изучили понятие функция. Изучили её график и научились находить область определения и область значений функции.
· промежутки знакопостоянства функции;
· промежутки монотонности функции.
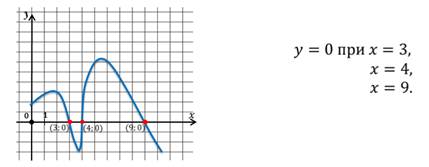
Нулями функции называют такие значения аргумента, при которых функция равна нулю.
В данном случае функция задана графически и мы определили нули функции по графику. Так же нули функции можно находить по формуле, с помощью которой задана функция.
Решив уравнение, мы найдём те значения х, при которых функция равна нулю.
Стоит обратить внимание на то, что не каждая функция имеет нули.
График не пересекает ось икс ни в одной точке.
Промежутки знакопостоянства функции
Функция принимает положительные значения:
И отрицательные значения:
Запишите промежутки знакопостоянства функции:
Положительные и отрицательные значения функции:
Промежутки монотонности функции
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции.
Функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Промежутками монотонности называют такие промежутки из области определения, на которых функция либо возрастает, либо убывает.
Опишем свойства функции:
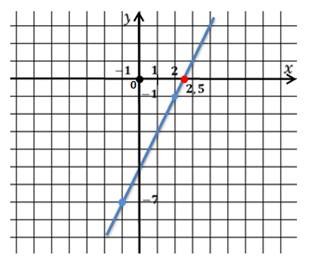
Графиком является прямая, поэтому для построения достаточно двух точек:
Найдём значения функции:
Областью определения и областью значений будет множество всех действительных чисел. Ведь х и у могут быть любыми числами.