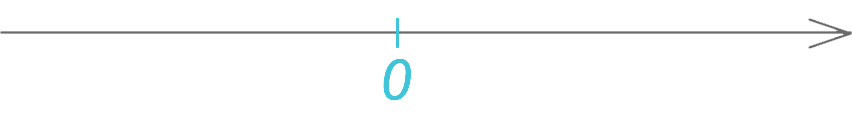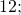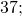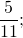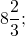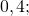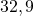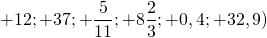Что такое положительные числа
Положительные и отрицательные числа
Вы будете перенаправлены на Автор24
Определение положительных и отрицательных чисел
Для определения положительных и отрицательных чисел воспользуемся координатной прямой, которая располагается горизонтально и направлена слева направо.
Началу отсчета на координатной прямой соответствует число нуль, которое не относится ни к положительным, ни к отрицательным числам.
Числа, соответствующие точкам координатной прямой, которые лежат правее от начала отсчета, называются положительными.
Числа, соответствующие точкам координатной прямой, которые лежат левее от начала отсчета, называются отрицательными.
Из данных определений вытекает, что множество всех отрицательных чисел противоположно множеству всех положительных чисел.
Отрицательные числа всегда записывают со знаком «–» (минус).
Примеры положительных чисел:
Все натуральные числа являются положительными.
Готовые работы на аналогичную тему
Примеры отрицательных чисел:
Для упрощения записи перед положительными числами часто не записывают знак «+» (плюс), а перед отрицательными знак «–» записывают всегда. В подобных случаях необходимо помнить, что запись «$17,4$» равносильна записи «$+17,4$», запись «$\sqrt<5>$» равносильна записи «$+\sqrt<5>$» и т.д.
Таким образом, можно использовать следующее определение положительных и отрицательных чисел:
Числа, записанные со знаком «+», называются положительными, а со знаком «–» – отрицательными.
Используется определение положительных и отрицательных чисел, которое основано на сравнении чисел:
Положительными числами являются числа больше нуля, а отрицательными числами – числа меньше нуля.
Таким образом, число нуль разделяет положительные и отрицательные числа.
Правила чтения положительных и отрицательных чисел
При чтении числа со знаком впереди него сначала читается его знак, а затем само число.
Например, «$+17$» читают «плюс семнадцать»,
«$-3 \frac<4><11>$» читают «минус три целых четыре одиннадцатых».
Стоит отметить, что названия знаков «плюс» и «минус» не склоняются, в то время как числа могут склоняться.
Например, «$x=-18$» можно читать как «икс равен минус восемнадцать», так и «икс равен минус восемнадцати».
Интерпретация положительных и отрицательных чисел
Положительные числа используются для обозначения увеличения какой-нибудь величины, прихода, прибавки, возрастание значения и т.д.
Отрицательные числа применяют для противоположных понятий – для обозначения уменьшения какой-нибудь величины, расхода, недостатка, долга, снижения значения и т.д.
Рассмотрим примеры.
Положительные и отрицательные числа часто используют для описания значений различных величин в измерительных приборах. Например, термометр для измерения температуры имеет шкалу, на которой отмечены положительные и отрицательные значения.
Принято отрицательные числа изображать синим цветом, что символизирует холод, низкую температуру, а положительные числа – красным цветом, что символизирует тепло, высокую температуру. Обозначение положительных и отрицательных чисел с помощью красного и синего цвета используется в различных ситуациях для выделения знака чисел.
Положительное число
Отрицательное число — элемент множества отрицательных чисел, которое (вместе с нулём) появилось в математике при расширении множества натуральных чисел. Цель расширения: обеспечить выполнение операции вычитания для любых чисел. В результате расширения получается множество (кольцо) целых чисел, состоящее из положительных (натуральных) чисел, отрицательных чисел и нуля.
Все отрицательные числа, и только они, меньше, чем нуль. На числовой оси отрицательные числа располагаются слева от нуля. Для них, как и для положительных чисел, определено отношение порядка, позволяющее сравнивать одно целое число с другим.
Содержание
Свойства отрицательных чисел
Отрицательные числа подчиняются практически тем же правилам, что и натуральные, но имеют некоторые особенности.
Исторический очерк
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.
Впервые отрицательные числа были частично узаконены в Китае, а затем (примерно с VII века) и в Индии, где трактовались как долги (недостача), или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата. Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.
Диофант в III веке уже знал правило знаков и умел умножать отрицательные числа. Однако и он рассматривал их лишь как временные значения.
В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Тем не менее теория отрицательных чисел долго находилась в стадии становления. Оживлённо обсуждалась, например, странная пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии.
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).
Положительные и отрицательные числа: определение, примеры
В этом материале мы объясним, что такое положительные и отрицательные числа. После того, как будут сформулированы определения, мы покажем на примерах, что это такое, и раскроем основной смысл этих понятий.
Что такое положительные и отрицательные числа
Для того чтобы объяснить основные определения, нам понадобится координатная прямая. Она будет расположена горизонтально и направлено слева направо: так будет удобнее для понимания.
Положительные числа – это те числа, которые соответствуют точкам в той части координатной прямой, которая расположена справа от начала отсчета.
Отрицательные числа – это те числа, которые соотносятся с точками в части координатной прямой, расположенной с левой стороны от начала отсчета (нуля).
Нуль, от которого выбираем направления, сам по себе не относится ни к отрицательным, ни к положительным числам.
Из данных выше определений следует, что положительные и отрицательные числа образуют некие множества, противоположные друг другу (положительные противопоставляются отрицательным, и наоборот). Ранее мы об этом уже упоминали в рамках статьи о противоположных числах.
Мы всегда записываем отрицательные числа с минусом.
В литературе также можно встретить определения положительных и отрицательных чисел, данные на основе наличия у них того или иного знака.
Положительное число – это число, имеющее знак плюс, а отрицательное – имеющее знак минус.
Положительные числа – это все числа, значение которых больше нуля. Отрицательные числа – это все числа, меньшие нуля.
Выходит, что нуль является своеобразным разделителем: он отделяет отрицательные числа от положительных.
Основной смысл положительных и отрицательных чисел
Мы уже дали основные определения, но для того, чтобы делать верные подсчеты, необходимо понять сам смысл положительности или отрицательности числа. Попробуем помочь вам это сделать.
Положительные и отрицательные числа
Чтобы понять, что из себя представляют положительные и отрицательные числа, давайте для начала начертим координатную прямую и отметим на ней точку 0 (ноль), которая считается началом отсчета.
Расположим ось в более привычном горизонтальном виде. Стрелка показывает положительное направление прямой (слева направо).
Сразу обратим внимание, что число “ноль” не относится ни к положительным, ни к отрицательным числам.
Положительные числа
Если мы начнем отмерять отрезки справа от нуля, то полученные отметки будут соответствовать положительным числам, равным расстояния от 0 до этих отметок. Таким образом мы получили числовую ось.
Полная запись положительных чисел включает знак “+” спереди, то есть +3, +7, +12, +21 и т.д. Но “плюс” обычно опускается и просто подразумевается:
Примечание: любое положительное число больше нуля.
Отрицательные числа
Если мы начнем отмерять отрезки слева от нуля, то вместо положительных получатся отрицательные числа, т.к. мы будем двигаться в противоположную от направления прямой сторону.
Примечание: любое отрицательное число меньше нуля.
Отрицательные числа как и положительные нужны для выражения различных математических, физических, экономических и прочих величин. Например:
Положительные числа
Положительные числа — это числа со знаком «+» перед ними. Знак «+» обычно не пишется (если перед числом не написан знак, то, по умолчанию, это число со знаком «+»).
— положительные числа. Перед этими числами не записан знак, значит, по умолчанию, перед ними стоит знак «плюс» (это сокращенная форма записи
Таким образом, +12=12, то есть +12 и 12 — это одно и то же число, только по-разному обозначенное.
Любое положительное число больше нуля.
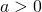
означает, что число a — положительное.
Все натуральные числа являются положительными.
На координатной прямой все положительные числа расположены правее нуля.
Любое положительное число на координатной прямой лежит правее любого отрицательного числа.
Число нуль не является ни положительным, ни отрицательным. Оно отделяет положительные числа от отрицательных.